Quantum logic and heuristics Tutorial on Quantum Models

Quantum logic and heuristics Tutorial on Quantum Models of Cognition and Decision Peter Kvam, Michigan State University

Information processing • The use of cues (indicators of the state of the world) is an integral part of decision making – Linguistic (prosody, pitch, tone, words) – Visual cues (shading, size for distance) – Internal states (hunger, fatigue, context / schemas, working memory content) • They must be organized in some way in order to be used – Knowing what cues to use when – What cues to prioritize – When context affects cue use

Heuristics • Focus on fast & frugal heuristics program – In particular on take the best (Gigerenzer & Goldstein, 1996) and the recognition heuristic (Goldstein & Gigerenzer, 2002) • Heuristic: decision strategy which ignores some amount of relevant information, often with the goal of faster / more accurate / frugal decisions – But see also other programs and definitions like Heuristics & Biases (Kahneman & Frederick, 2002) or satisficing (Simon, 1990)

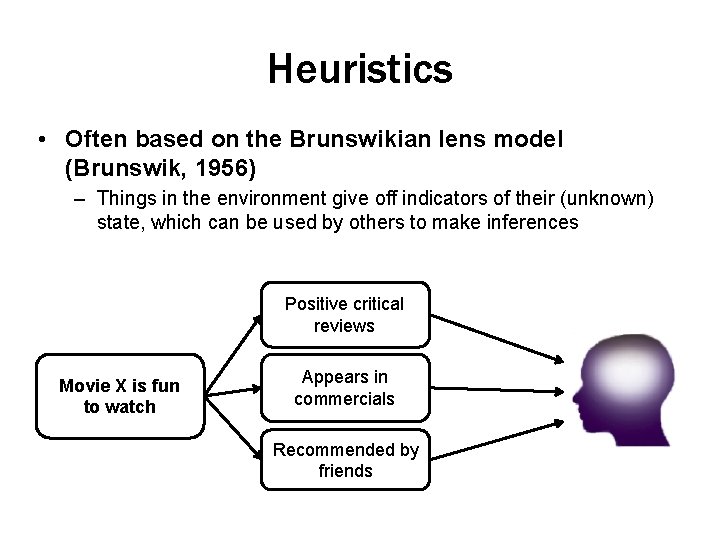
Heuristics • Often based on the Brunswikian lens model (Brunswik, 1956) – Things in the environment give off indicators of their (unknown) state, which can be used by others to make inferences Positive critical reviews Movie X is fun to watch Appears in commercials Recommended by friends

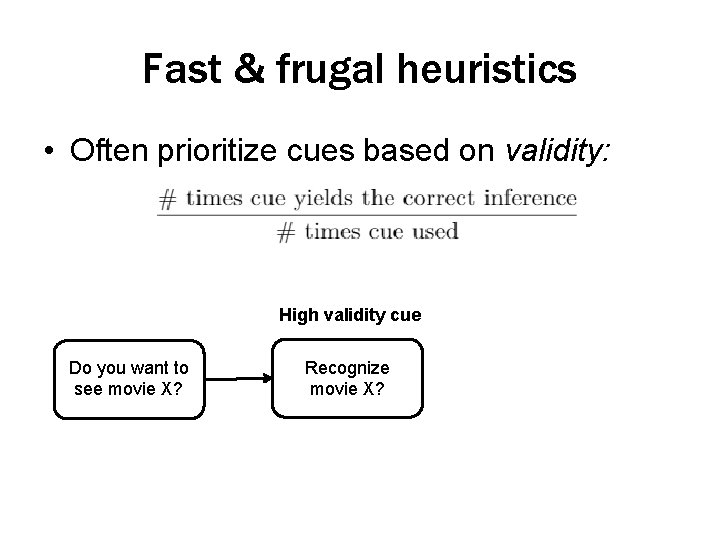
Fast & frugal heuristics • Often prioritize cues based on validity:

Fast & frugal heuristics • Often prioritize cues based on validity: Do you want to see movie X?

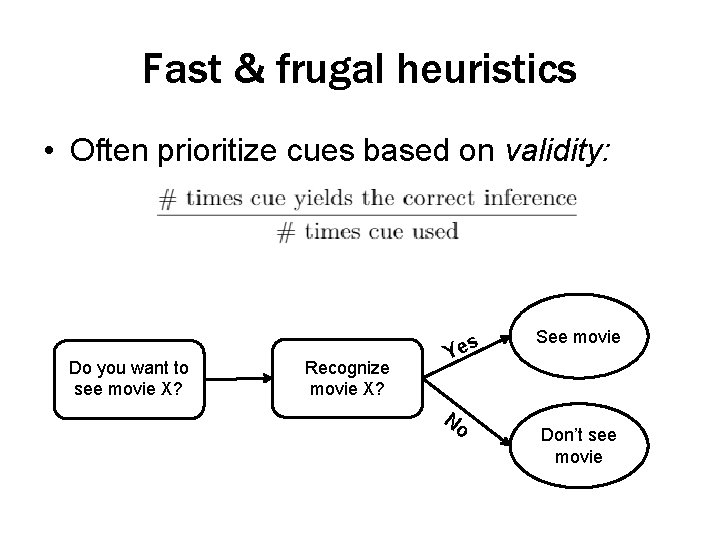
Fast & frugal heuristics • Often prioritize cues based on validity: High validity cue Do you want to see movie X? Recognize movie X?

Fast & frugal heuristics • Often prioritize cues based on validity: Do you want to see movie X? Recognize movie X? s Ye No See movie Don’t see movie

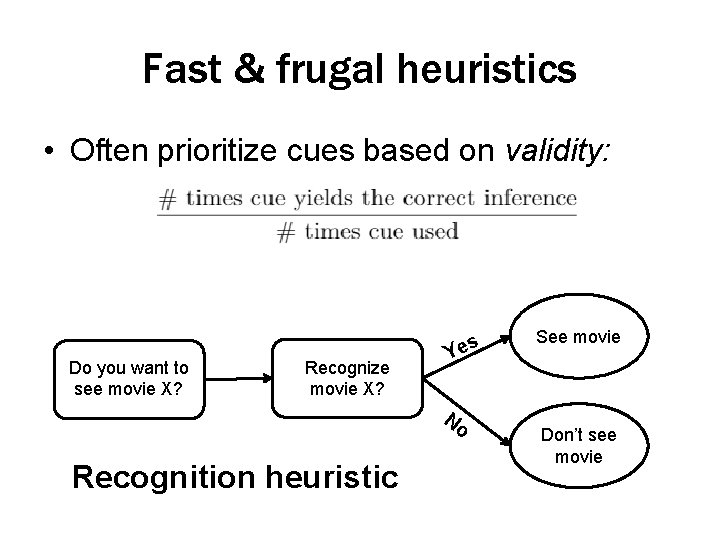
Fast & frugal heuristics • Often prioritize cues based on validity: Do you want to see movie X? Recognize movie X? s Ye No Recognition heuristic See movie Don’t see movie

Examples of heuristics • Single cue – Recognition: Select one alternative if it is recognized another is not (or select alternative it if is recognized, don’t select if not) • Serial order: – Take-the-best: Check cues in order of validity, use first distinguishing cue to make decision • Multiple-cue – Tallying: Count the number cues favoring alternative A and B, choose A if greater than the number favoring B (& vice versa) – Weighted additive: (essentially regression) Multiply each cue value by a weight, choose A if greater than B (or greater than some criterion value)

Advantages of heuristics • Simplicity – Ignore covariance between cues – Restricted parameter space • Often no free parameters • Low computational complexity • Less data needed for parameter estimation (see bias-variance) – Easy to communicate to others • Prescriptive properties

Computational basis • In their current form, heuristics use a classical logic to implement rules • Belief representation (binary) 0 1 – True [1] or False [0] – Sequences of bits describe more complex beliefs (about multiple events, continuous values, etc) • Belief change is implemented using logical operations (logic gates)

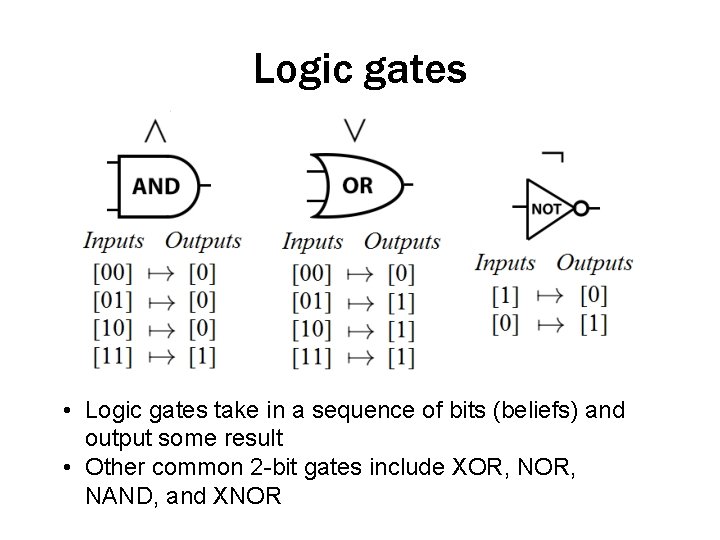
Logic gates • Logic gates take in a sequence of bits (beliefs) and output some result • Other common 2 -bit gates include XOR, NOR, NAND, and XNOR

A simple example • Logic operations can be written as logical statements or circuits. We’ll do the former first. • Rule: Say hello (R 1) if you recognize a person’s face (F) and their gait (G) • R 0 controls initial beliefs / desire to say hello (prior)

A simple example • A lack of face recognition (F = 0) or gait recognition (G = 0) will prevent a response • In this scenario, prior beliefs / preferences don’t factor into response – This could be adjusted to create stricter or more lenient rules

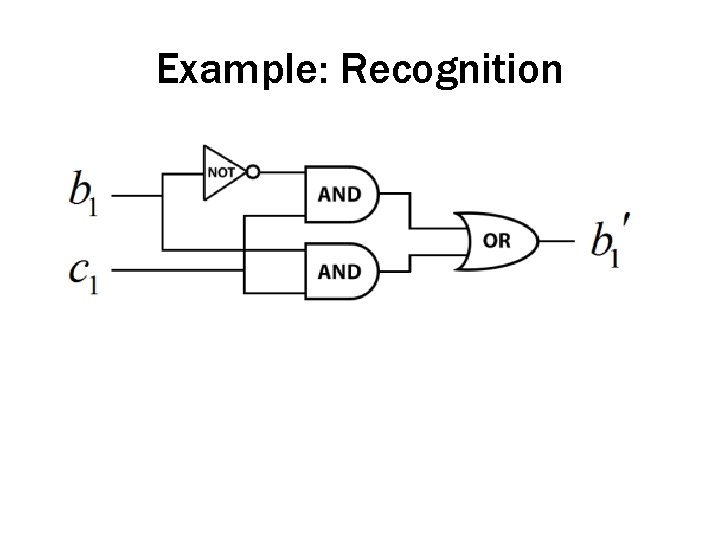
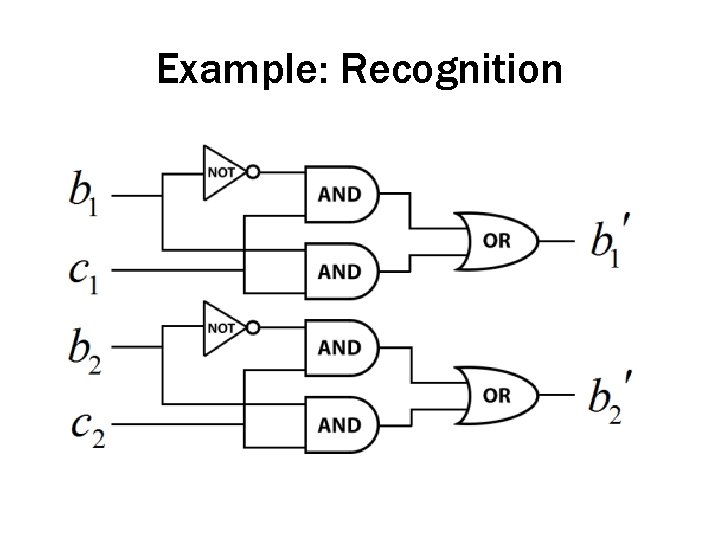
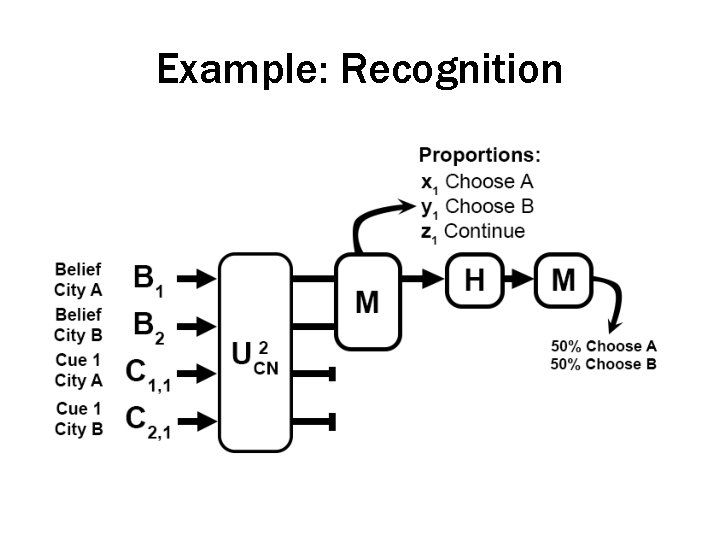
Example: Recognition • Recognition heuristic: – (1 alternative) Check if the alternative is recognized • If so, select the alternative • If not, do not select the alternative – (2 alternative) Check if each alternative is recognized • If one is recognized, select it (as higher on the criterion value) • If both are recognized or neither is recognized, choose randomly or use other cues

Example: Recognition Suppose we are deciding which of two cities is larger… b 1 = Believe that Atlanta is large b 2 = Believe that Bakersfield is large c 1 = Recognize Atlanta c 2 = Recognize Bakersfield

Example: Recognition

Example: Recognition

Things to note • All inputs and outputs are binary – Hard to represent continuous values, which require much longer bit strings

Things to note • All inputs and outputs are binary – Hard to represent continuous values, which require much longer bit strings • Circuit is deterministic – If a person sticks to this rule, there should be no behavioral variability – If a competitor knows the inputs and rule, they can predict a person’s behavior (exploitable) Think rock, paper, scissors

Things to note • All inputs and outputs are binary – Hard to represent continuous values, which require much longer bit strings • Circuit is deterministic – If a person sticks to this rule, there should be no behavioral variability – If a competitor knows the inputs and rule, they can predict a person’s behavior (exploitable) • Steps (cue inspections) are executed in serial – May take quite some time to get through – Doesn’t describe actual behavior / brain very well

Things to note • Heuristics in their current formulation obey all the laws of classical logic & probability Logical basis of the law of total probability

But these are violated in human decisions! Many of these we talked about today. • Order effects – Question order, primacy, recency (Trueblood & Busemeyer, 2011; Wang et al, 2014) • Violations of the sure thing principle – Disjunction effect in game theory (Tversky & Shafir, 1992) • Violations of dynamic consistency – Actions conflict with planning (Barkan & Busemeyer, 2003) • Violations of the law of total probability – Sequential judgment & decisions (Kvam et al, 2015; Townsend et al, 2000)

Quantum logic • One solution to these problems is to reconstruct heuristics using an alternative framework • Quantum logic is well-studied and used in quantum information / computing

Quantum logic • Belief representation – Qubits exist in a continuous superposition of 0 and 1 • State collapses onto one or the other when measured • Probability given by squared amplitude along corresponding dimension

Characteristics of qubits • Allow for modeling of truly stochastic behavior – Potentially descriptively more accurate • Permits an agent to behave unpredictably – Rock paper scissors, matching pennies, other competitive scenarios • Continuous & uncertain beliefs and cue values – Continuous values used in recognition, familiarity – Reflects continuous values in the world – Uncertainty can be used rather than ignored

Qubits - vectors • Qubits can be represented using the probability amplitudes along their dimensions – Either as a sum of the bases: – Or as a vector: – Note that and

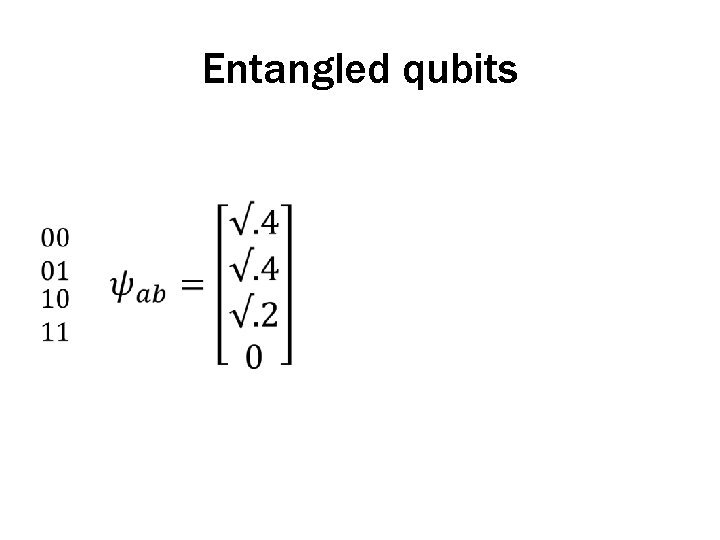
Combining qubits • Compound states – Recall that bits can be strung together in the classical framework by placing them in sequence – Qubits can be paired by taking their Kronecker (outer) product

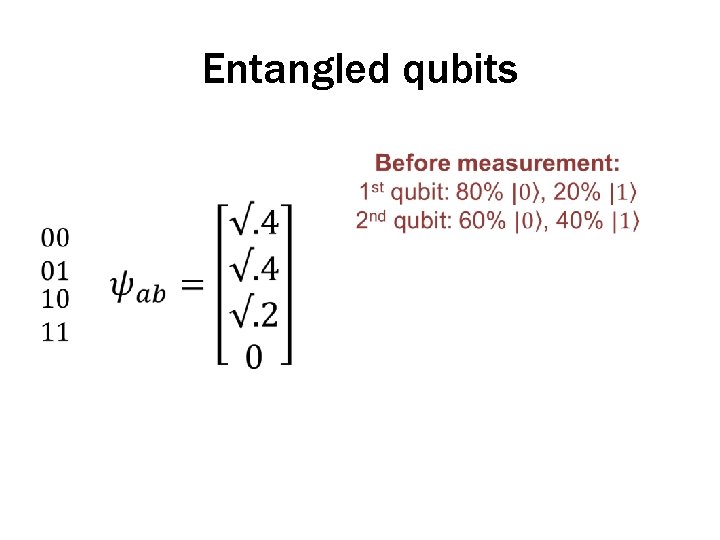
Entangled qubits •

Entangled qubits

Entangled qubits

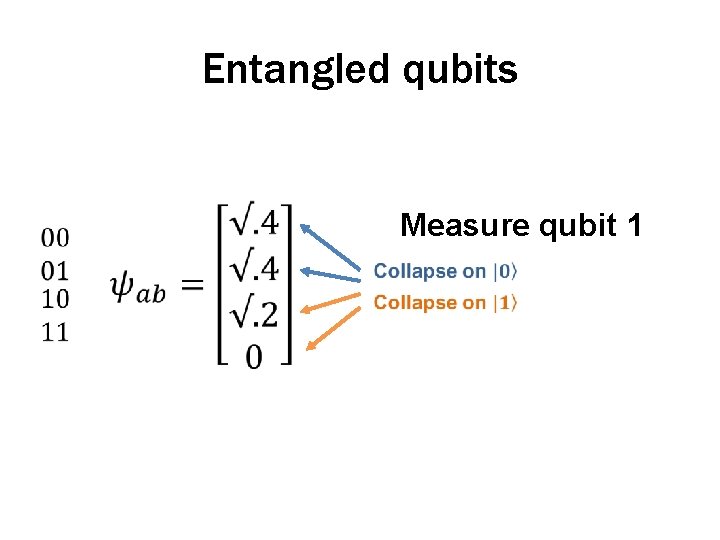
Entangled qubits Measure qubit 1

Entangled qubits

Entangled qubits

Entangled qubits

Entangled qubits • Allows for measurement of beliefs about criteria (e. g. city size) to affect beliefs about cues (e. g. university presence) and vice versa • Produces order effects in measurements • Can result in the hindsight bias

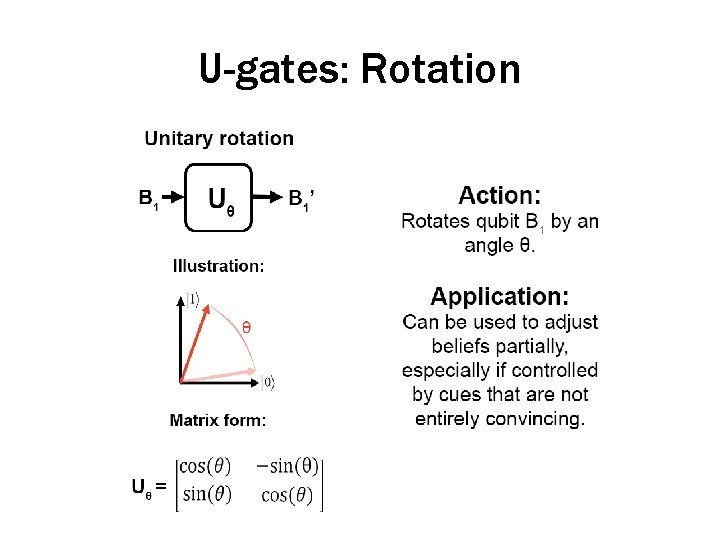
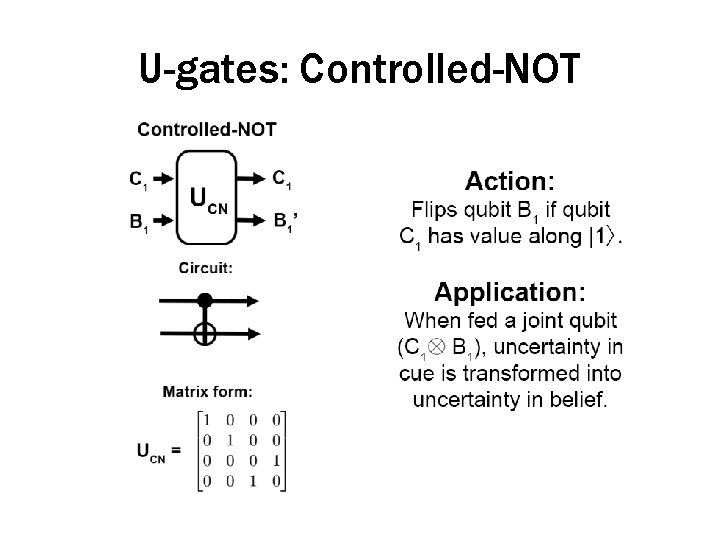
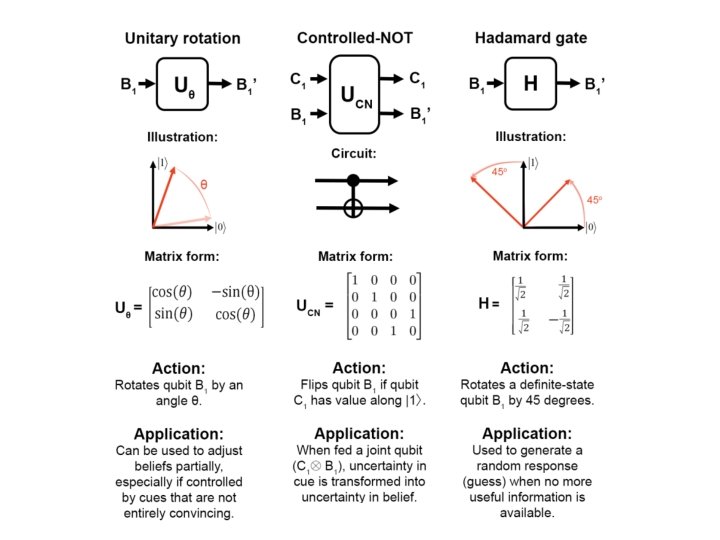
U-gates • Many U-gates mimic the actions performed by classical logic gates – For example, the Pauli-X matrix implements NOT – Simply flips a qubit (switching |0� with |1� coordinates) • However, there is considerably more flexibility in possible quantum gates

U-gates: Rotation

U-gates: Controlled-NOT

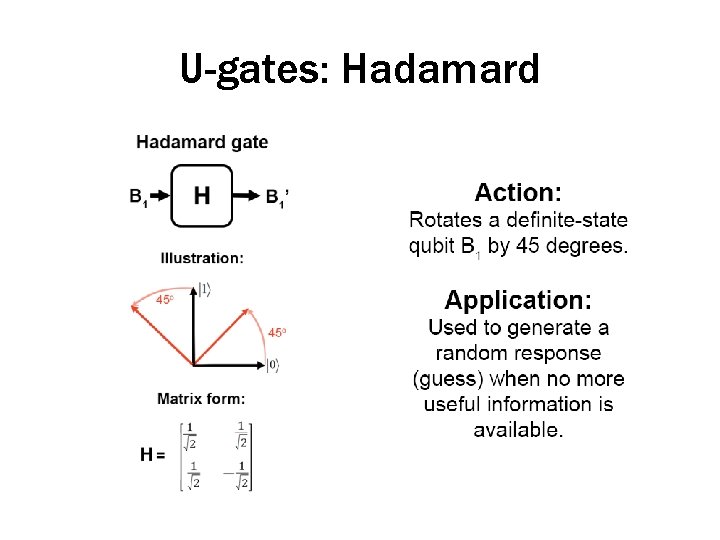
U-gates: Hadamard

More about U-gates • Reversible – Any transformation can be undone by applying its inverse • Can be useful for modling backward induction problems – Once beliefs are measured, the original state cannot be obtained (if it was uncertain) • Can be applied to perform any classical probability logic operation – Universal gates (see Toffoli gate) – Quantum logic implementation can be seen as a general form of the classical logic we saw earlier

Example: Recognition

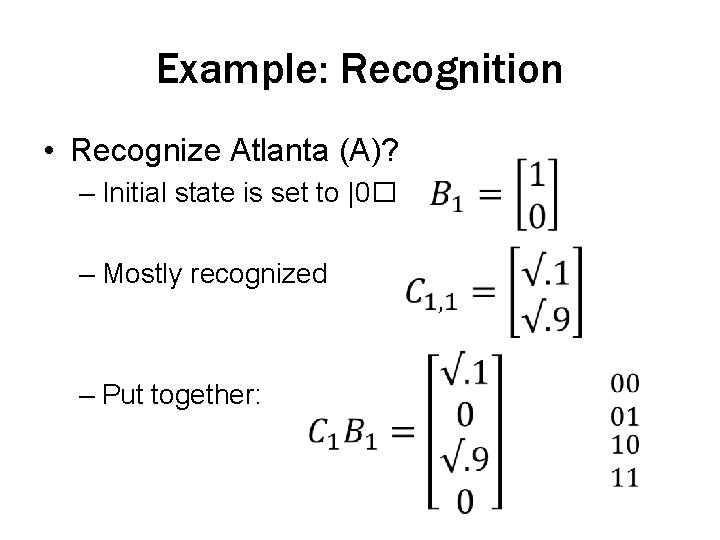
Example: Recognition • Recognize Atlanta (A)? – Initial state is set to |0� – Mostly recognized – Put together:

Example: Recognition • Processing cue 1 & criterion belief 1 (recognition and size of Atlanta)

Example: Recognition • Processing cue 1 & criterion belief 1 (recognition and size of Atlanta)

Example: Recognition • Processing cue 1 & criterion belief 1 (recognition and size of Atlanta)

Example: Recognition • Uncertainty in the cue values are reflected in uncertainty in criterion beliefs 1 st qubit: 10% [0], 90% [1] 2 nd qubit: 10% [0], 90% [1] Entangled: Measuring qubit 1 = [1] means that qubit 2 will be = [1]

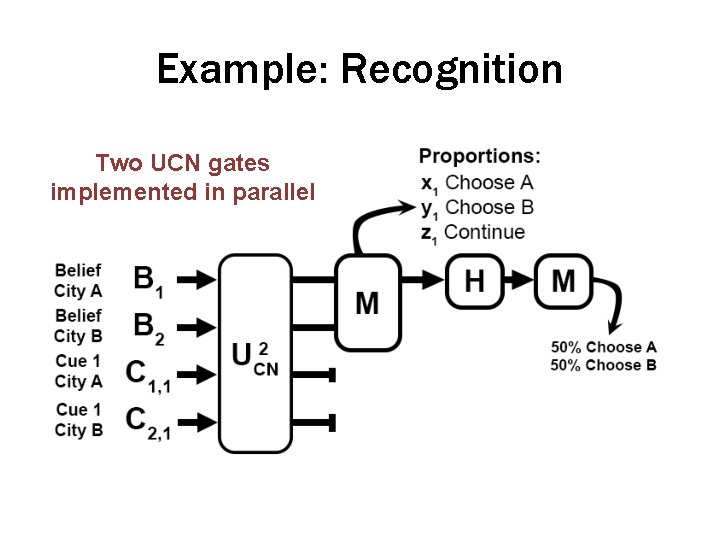
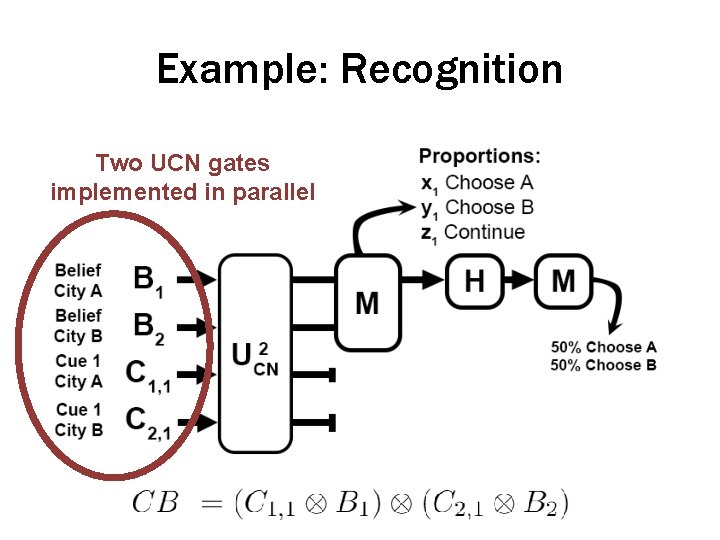
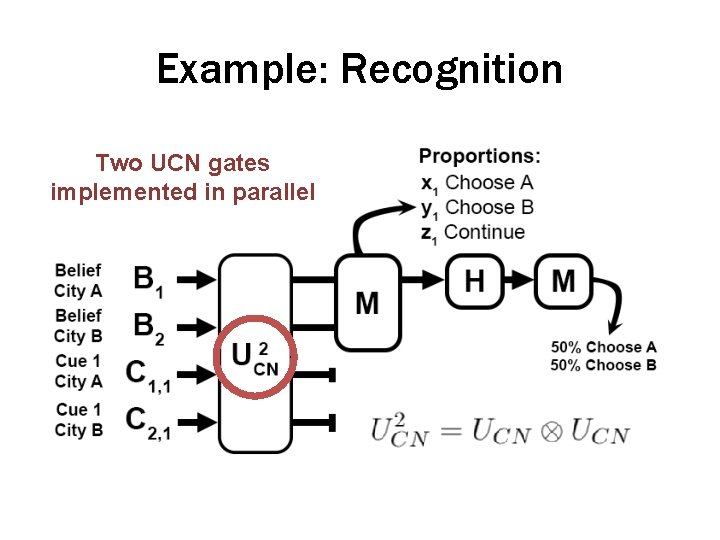
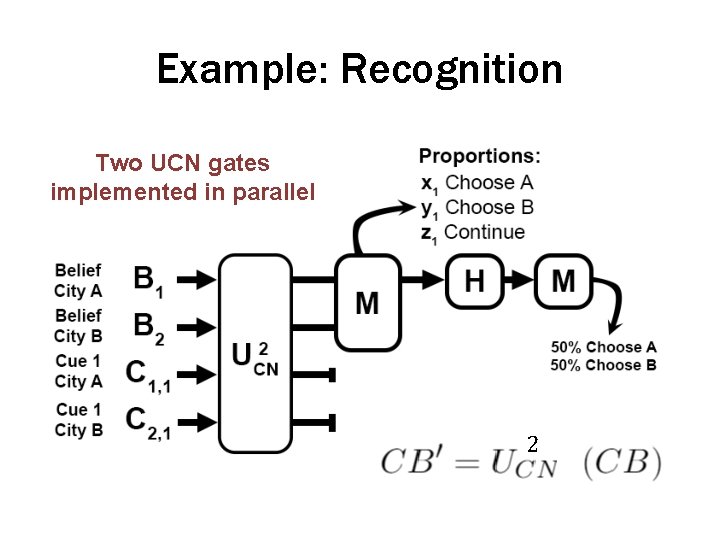
Example: Recognition Two UCN gates implemented in parallel

Example: Recognition Two UCN gates implemented in parallel

Example: Recognition Two UCN gates implemented in parallel

Example: Recognition Two UCN gates implemented in parallel 2

Example: Recognition • Can look at different parts of CB’ individually for simplicity (don’t have to look at complete 16 dimensional vector)

Example: Recognition • Can look at different parts of CB’ individually for simplicity (don’t have to look at complete 16 dimensional vector) 45% chance of [11], 5% chance of [00] -> 50% chance of choosing randomly 45% chance of [10] -> 45% chance of selecting Atlanta as larger 5% chance of [01] -> 5% chance of selecting Bakersfield as larger

Things to note • Uncertainty in cue values is incorporated as uncertainty in criterion beliefs – Rather than assuming uncertainty away or skipping missing / uncertain cues • Behavior is stochastic rather than deterministic • Probability of proceeding to further stages even if cue values are (partially) known – Results in use of lower-validity cues

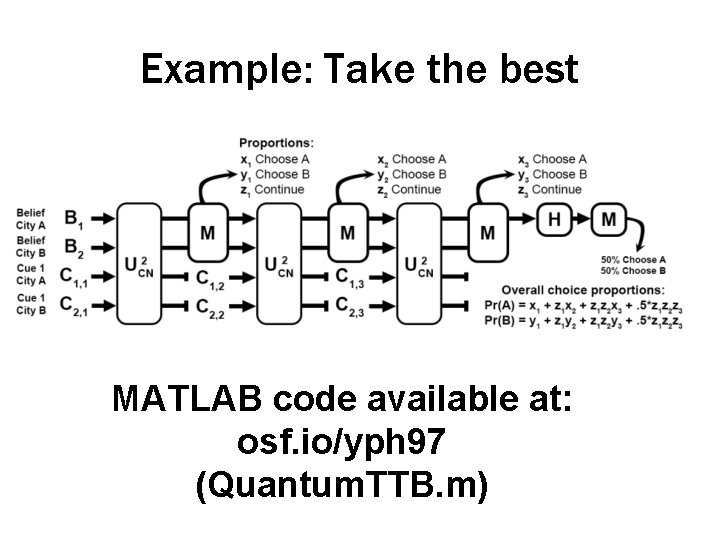
Example: Take the best • Take the best: 1. Order cues by their validity 2. Check the (next) most valid cue 3. If one choice alternative has that cue and the other does not, choose the alternative with the cue. 4. If both or neither has the cue, and there are more cues, return to 2. 5. Choose randomly between alternatives

Example: Take the best MATLAB code available at: osf. io/yph 97 (Quantum. TTB. m)

Hindsight bias • RAFT model – Unknown cue values are updated after criterion information is received – Updated cue values are used to make retrospective confidence judgment Unknown cue value Prospective confidence Criterion information

Hindsight bias • RAFT model – Unknown cue values are updated after criterion information is received – Updated cue values are used to make retrospective confidence judgment Known cue value Retrospective confidence Overconfidence (hindsight bias) Criterion information

Hindsight bias • Quantum account of hindsight (nearly the same) – Uncertain cue value is entangled with criterion beliefs as cue information is processed – Updating criterion beliefs causes cue beliefs to change as well – Revised cue beliefs are used to judge retrospective confidence Cue-criterion belief entanglement Uncertain cue value Beliefs collapse on true criterion value Prospective confidence Criterion information

Hindsight bias • Quantum account of hindsight (nearly the same) – Uncertain cue value is entangled with criterion beliefs as cue information is processed – Updating criterion beliefs causes cue beliefs to change as well – Revised cue beliefs are used to judge retrospective confidence Revised cue beliefs Retrospective confidence Overconfidence (hindsight bias) Criterion information

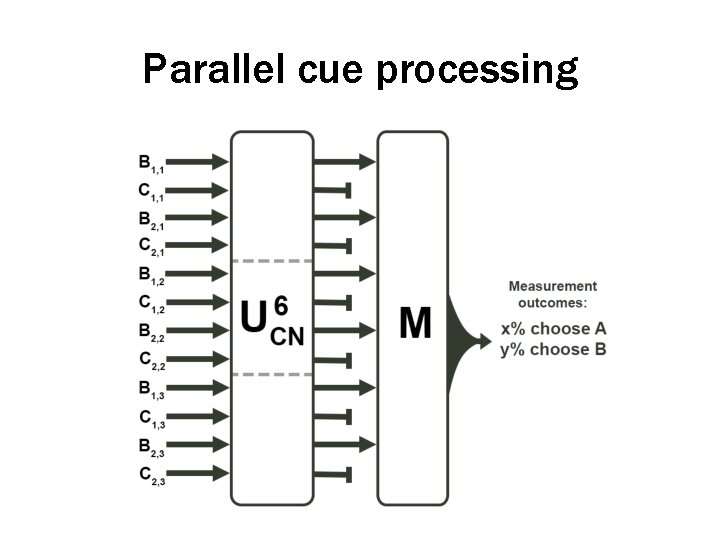
Parallel cue processing • We are not restricted to processing only one pair of cues at a time • Different U-gates can be combined (as we saw) by taking their Kronecker product – As can belief states • Measurement operators then responsible for implementing different decision rules

Parallel cue processing

Parallel cue processing • Can implement a variety of strategies: – Weighted additive (WADD), where cues are multiplied by some coefficient and added together to compute a criterion value – Tallying, same as weighted additive but all coefficients are fixed to 1 • Or implement others: – Dominance-based (e. g. check all cases where A has equal or better cue values than B) – Simultaneous sets (e. g. 2 or 3 cues at one time)

Extensions • Cues can control the action of much more complex gates – For example, could trigger random walks using unitary matrices as in Busemeyer et al (2006), Kvam et al (2015), Wang & Busemeyer (2016) – Allows for modeling of cue-based confidence judgments and response times • Hindsight bias – Revision of criterion beliefs affects (entangled) cue beliefs – Revisiting revised cue beliefs yields higher confidence – Same explanation as RAFT model (Hertwig et al, 1997)

Uncertainty and entropy • An interesting aspect of the quantum information approach is how it relates to uncertainty – Heuristics often deal with epistemic and aleatory uncertainty • Epistemic uncertainty: reducible with knowledge, unpredictability due to lack of information – Characterized by classical Shannon entropy (uncertainty about the state of a bit string) • Aleatory uncertainty: in principle irreducible, cannot be eliminated with more knowledge • Ontic uncertainty: Uncertainty about the state of something, introduced in the quantum framework (may be mistaken for aleatory uncertainty) – Characterized by von Neumann entropy

Benefits of heuristics • Structure and rules – Gives definite sets of processing rules to implement – Provides theory for constructing quantum processing rules – Search, stopping, (sort of) decision rules • Simplicity – Avoid estimating covariance between cues – Deterministic structures can reduce model complexity – Excellent as prescriptive strategies (communicable) • Ecologically adaptive (suited to environments)

Benefits of quantum logic • Allows for continuous, probabilistic cue and criterion beliefs – Greater descriptive power, closer to real structure of cues & beliefs in the world • Allows for strategies that incorporate and take advantage of uncertainty • Parallel cue processing – With rules implemented by measurement operators (applied either in parallel or serial) – Can easily combine rules to go from serial to parallel • New predictions: entanglement – Hindsight bias with revision of cue & criterion beliefs

Conclusions • Heuristics provide a new ground for building and testing quantum models – Provide theory, structure, and desirable properties of strategies • Quantum logic and information processing bring descriptive accuracy to heuristics – Don’t have to predict 100% adherence – Account for influence of lower-validity cues • Opens up new questions that might not otherwise have been considered

Questions? Supported by a fellowship from the National Science Foundation (Grant No. DGE-1424871)