Quantum Information Theory Patrick Hayden Mc Gill 4

Quantum Information Theory Patrick Hayden (Mc. Gill) 4 August 2005, Canadian Quantum Information Summer School

Overview § Part I: § What is information theory? § § § What does it have to do with quantum mechanics? Noise in the quantum mechanical formalism § § § Entropy, compression, noisy coding and beyond Density operators, the partial trace, quantum operations Some quantum information theory highlights Part II: § § Resource inequalities A skeleton key

Information (Shannon) theory § A practical question: § § A mathematico epistemological question: § § How to best make use of a given communications resource? How to quantify uncertainty and information? Shannon: Solved the first by considering the second. § A mathematical theory of communication [1948] The §

Quantifying uncertainty § § Entropy: H(X) = x p(x) log 2 p(x) Proportional to entropy of statistical physics Term suggested by von Neumann (more on him later) Can arrive at definition axiomatically: § § H(X, Y) = H(X) + H(Y) for independent X, Y, etc. Operational point of view…

Compression Source of independent copies of X X X 21 X …n If X is binary: 0000100111010100010101100101 About n. P(X=0) 0’s and n. P(X=1) 1’s {0, 1}n: 2 n possible strings 2 n. H(X) typical strings Can compress n copies of X to a binary string of length ~n. H(X)

Typicality in more detail § § Let xn = x 1, x 2, …, xn with xj 2 X We say that xn is typical with respect to p(x) if § § § For all a 2 X with p(a)>0, |1/n N(a|xn) – p(a) | < / |X| For all a 2 X with p(a) = 0, N(a|xn)=0. For >0, the probability that a random string Xn is typical goes to 1. If xn is typical, 2 n[H(X)+ ]· p(xn) · 2 n[H(X) ] The number of typical strings is bounded above by 2 n[H(X)+ ]

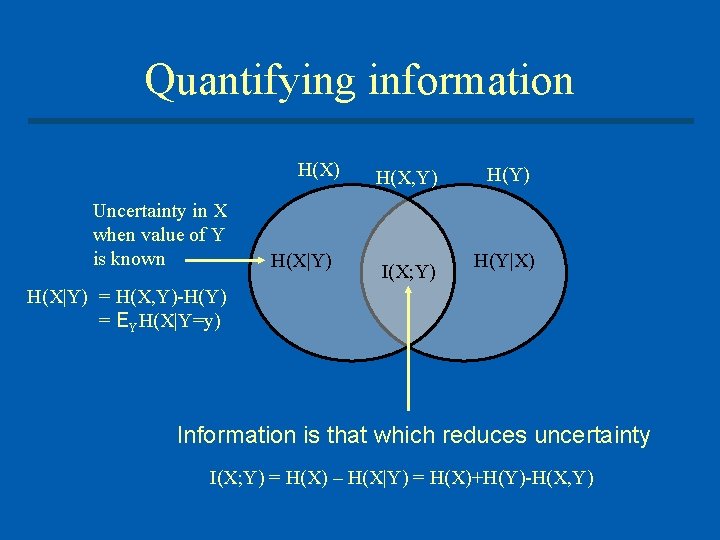
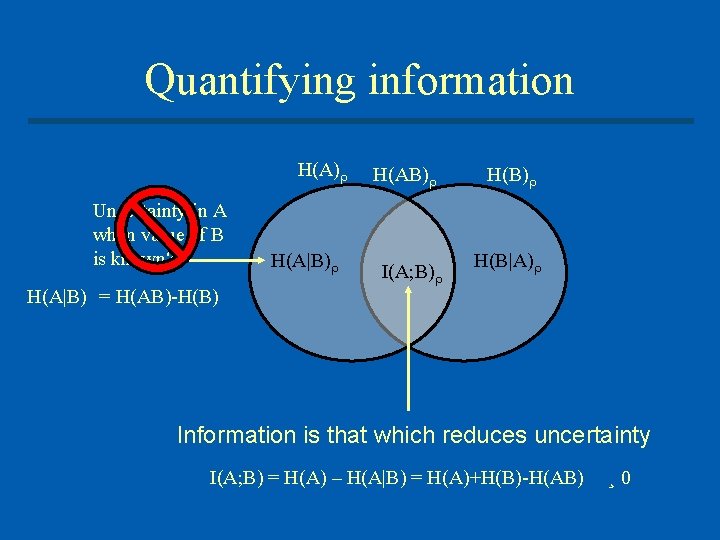
Quantifying information H(X) Uncertainty in X when value of Y is known H(X|Y) H(X, Y) I(X; Y) H(Y|X) H(X|Y) = H(X, Y)-H(Y) = EYH(X|Y=y) Information is that which reduces uncertainty I(X; Y) = H(X) – H(X|Y) = H(X)+H(Y)-H(X, Y)

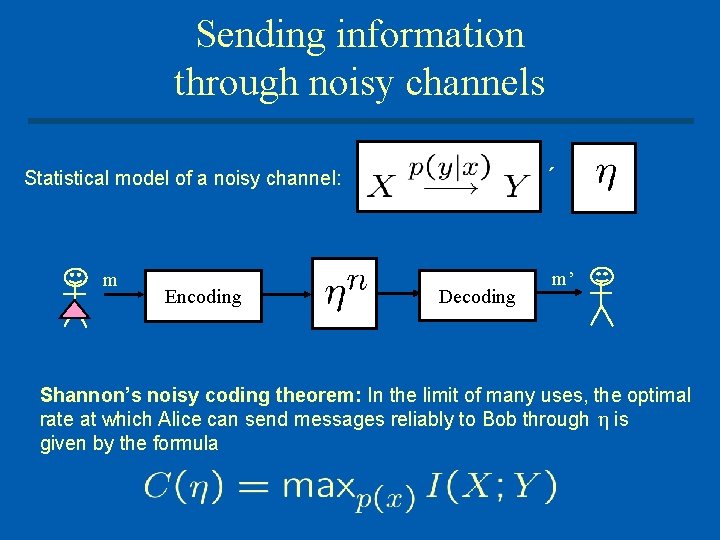
Sending information through noisy channels ´ Statistical model of a noisy channel: m Encoding Decoding m’ Shannon’s noisy coding theorem: In the limit of many uses, the optimal rate at which Alice can send messages reliably to Bob through is given by the formula

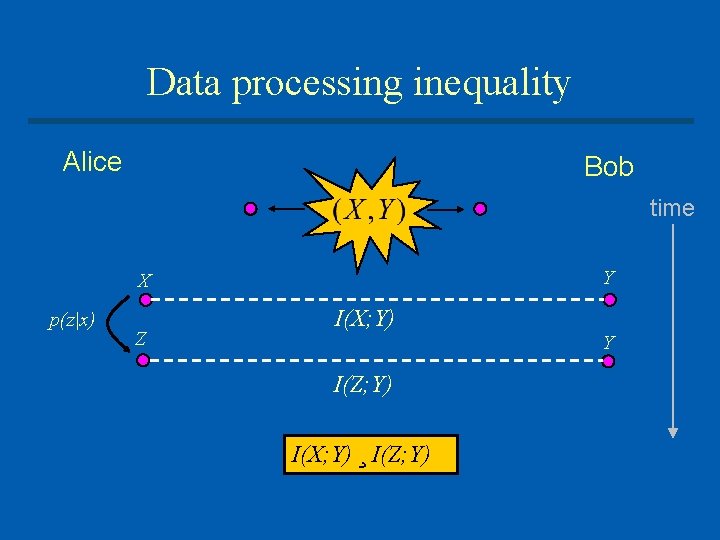
Data processing inequality Alice Bob time Y X p(z|x) Z I(X; Y) I(Z; Y) I(X; Y) ¸ I(Z; Y) Y

Optimality in Shannon’s theorem m Encoding Xn Yn Decoding m’ Shannon’s noisy coding theorem: In the limit of many uses, the optimal rate at which Alice can send messages reliably to Bob through is given by the formula Assume there exists a code with rate R and perfect decoding. Let M be the random variable corresponding to the uniform distribution over messages. n. R = H(M) = I(M; M’) · I(M; Yn) · I(Xn; Yn) · j=1 n I(Xj, Yj) · n¢maxp(x) I(X; Y) Perfect decoding: M=M’ M has n. R bits of entropy Term by term Some fiddling Data processing

Shannon theory provides § Practically speaking: § § Conceptually speaking: § § A holy grail for error correcting codes A operationally motivated way of thinking about correlations What’s missing (for a quantum mechanic)? § Features from linear structure: Entanglement and non orthogonality

Quantum Shannon Theory provides § § General theory of interconvertibility between different types of communications resources: qubits, cbits, ebits, cobits, sbits… Relies on a § Major simplifying assumption: Computation is free § Minor simplifying assumption: Noise and data have regular structure

Before we get going: Some unavoidable formalism § We need quantum generalizations of: § § § Probability distributions (density operators) Marginal distributions (partial trace) Noisy channels (quantum operations)

Mixing quantum states: The density operator Draw | xi with probability p(x) Perform a measurement {|0 i, |1 i}: Probability of outcome j: qj = x p(x) |hj| xi |2 = x p(x) tr[|jih j| xih x|] = tr[ |jih j| ], where Outcome probability is linear in

Properties of the density operator § is Hermitian: § § is positive semidefinite: § § h | | i = x p(x) h | xih x| i¸ 0 tr[ ] = 1: § § y = [ x p(x) | xih x|]y = x p(x) [| xih x|]y = tr[ ] = x p(x) tr[| xih x|] = x p(x) = 1 Ensemble ambiguity: § I/2 = ½[|0 ih 0| + |1 ih 1|] = ½[|+ih+| + | ih |]

The density operator: examples Which of the following are density operators?

The partial trace A {Mk} AB § § § Suppose that AB is a density operator on A B Alice measures {Mk} on A Outcome probability is qk = tr[ (Mk IB) AB] § § § Define A = tr. B[ AB] = j Bhj| AB|ji. B. Then qk = tr[ Mk A ] A describes outcome statistics for all possible experiments by Alice alone

Purification A § | i § § § Suppose that A is a density operator on A Diagonalize A = i i | iih i| Let | i = i i 1/2 | ii. A|ii. B Note that A = tr. B[ ] | i is a purification of Symmetry: A= A and B have same non zero eigenvalues

Quantum (noisy) channels: Analogs of p(y|x) What reasonable constraints might such a channel : A! B satisfy? 1) Take density operators to density operators 2) Convex linearity: a mixture of input states should be mapped to a corresponding mixture of output states All such maps can, in principle, be realized physically Must be interpreted very strictly Require that ( IC)( AC) always be a density operator too Doesn’t come for free! Let T be the transpose map on A. If | i = |00 i. AC + |11 i. AC, then (T IC)(| ih |) has negative eigenvalues The resulting set of transformations on density operators are known as trace-preserving, completely positive maps

Quantum channels: examples § § Adjoining ancilla: |0 ih 0| Unitary transformations: U Uy Partial trace: AB tr. B[ AB] That’s it! All channels can be built out of these operations: |0 i U

Further examples § § The depolarizing channel: (1 p) + p I/2 The dephasing channel j hj| |ji |0 i Equivalent to measuring {|ji} then forgetting the outcome

One last thing you should see. . . § § What happens if a measurement is preceded by a general quantum operation? Leads to more general types of measurements: Positive Operator Valued Measures (forevermore POVM) {Mk} such that Mk ¸ 0, k Mk = 1 Probability of outcome k is tr[Mk ]

POVM’s: What are they good for? Try to distinguish | 0 i=|0 i and | 1 i = |+i = (|0 i+|1 i)/21/2 States are non-orthogonal, so projective measurements won’t work. Let N = 1/(1+1/21/2). Exercise: M 0 = N |1 ih 1|, M 1 = N |-ih-|, M 2 = I – M 0 – M 1 is a POVM Note: * Outcome 0 implies | 1 i * Outcome 1 implies | 0 i * Outcome 2 is inconclusive Instead of imperfect distinguishability all of the time, the POVM provides perfect distinguishability some of the time.

Notions of distinguishability Basic requirement: quantum channels do not increase “distinguishability” Fidelity Trace distance F( , )=[Tr( 1/2)]2 T( , )=| - |1 F=0 for perfectly distinguishable F=1 for identical T=2 for perfectly distinguishable T=0 for identical F( , )=max |h | i|2 T( , )=2 max|p(k=0| )-p(k=0| )| where max is over measurements {Mk} F( ( ), ( )) ¸ F( , ) T( , ) ¸ T( ( , ( )) Statements made today hold for both measures

Back to information theory!

Quantifying uncertainty § § Let = x p(x) | xih x| be a density operator von Neumann entropy: H( ) = tr [ log ] Equal to Shannon entropy of eigenvalues Analog of a joint random variable: § § AB describes a composite system A B H(A) = H( tr. B AB)

Quantifying uncertainty: examples § § § H(| ih |) = 0 H(I/2) = 1 H( ) = H( ) + H( ) H(I/2 n) = n H(p © (1 p) ) = H(p, 1 p) + p. H( ) + (1 p)H( )

Compression Source of independent copies of AB: No statistical assumptions: Just quantum mechanics! … (aka typical subspace) A B A B B n dim(Effective supp of B n ) ~ 2 n. H(B) Can compress n copies of B to a system of ~n. H(B) qubits while preserving correlations with A [Schumacher, Petz]

The typical subspace § § Diagonalize = x p(x) |exihex| Then n = xn p(xn) |exn ihexn| The typical projector t is the projector onto the span of the |exn ihexn| such that xn is typical tr[ n t] ! 1 as n ! 1

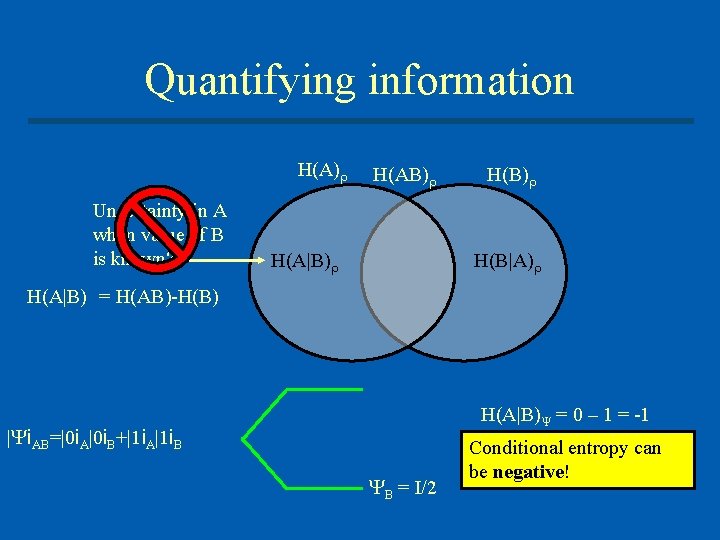
Quantifying information H(A) Uncertainty in A when value of B is known? H(AB) H(B|A) H(A|B) = H(AB)-H(B) H(A|B) = 0 – 1 = -1 | i. AB=|0 i. A|0 i. B+|1 i. A|1 i. B B = I/2 Conditional entropy can be negative!

Quantifying information H(A) Uncertainty in A when value of B is known? H(A|B) = H(AB)-H(B) H(A|B) H(AB) I(A; B) H(B|A) Information is that which reduces uncertainty I(A; B) = H(A) – H(A|B) = H(A)+H(B)-H(AB) ¸ 0

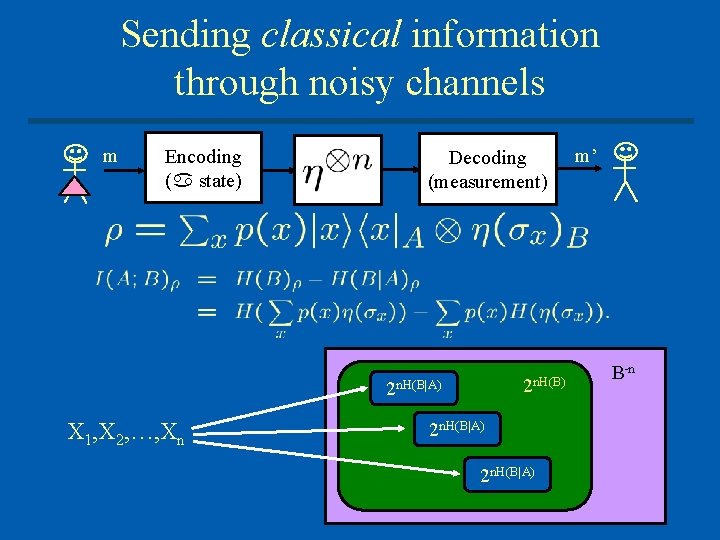
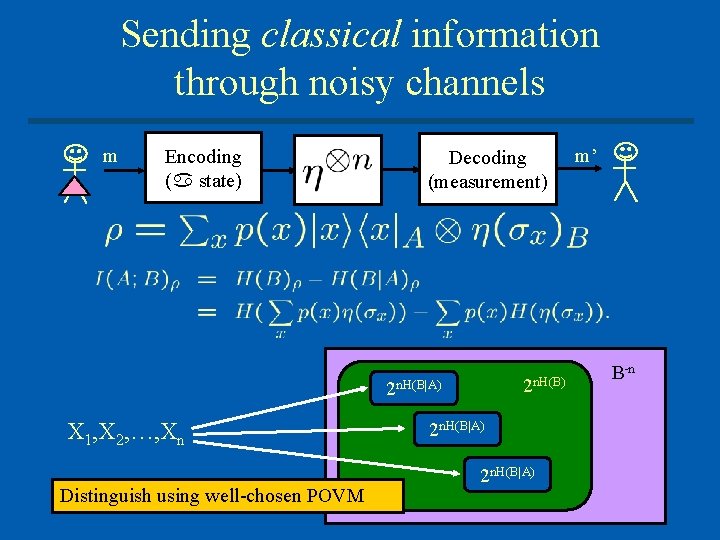
Sending classical information through noisy channels Physical model of a noisy channel: (Trace preserving, completely positive map) m Encoding ( state) Decoding (measurement) m’ HSW noisy coding theorem: In the limit of many uses, the optimal rate at which Alice can send messages reliably to Bob through is given by the (regularization of the) formula where

Sending classical information through noisy channels m Encoding ( state) Decoding (measurement) 2 n. H(B|A) X 1, X 2, …, Xn 2 n. H(B|A) m’ B n

Sending classical information through noisy channels m Encoding ( state) Decoding (measurement) 2 n. H(B|A) X 1, X 2, …, Xn Distinguish using well-chosen POVM 2 n. H(B|A) m’ B n

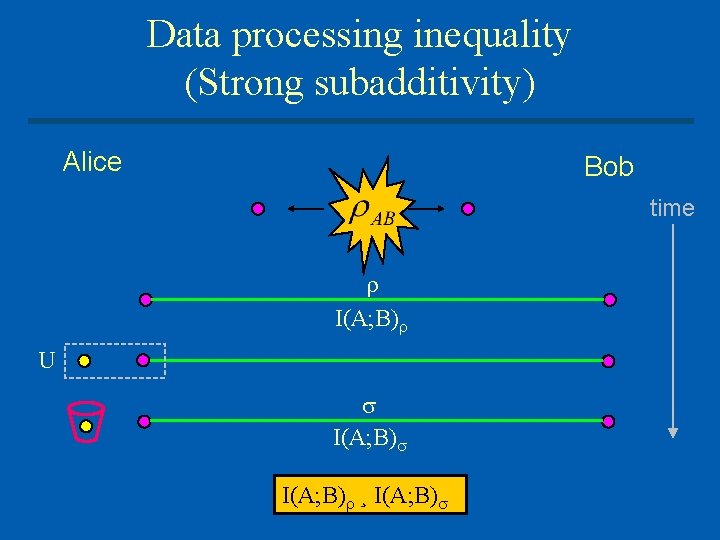
Data processing inequality (Strong subadditivity) Alice Bob time I(A; B) U I(A; B) ¸ I(A; B)

Optimality in the HSW theorem m Encoding ( state) m Decoding (measurement) m’ where Assume there exists a code with rate R with perfect decoding. Let M be the random variable corresponding to the uniform distribution over messages. n. R = H(M) = I(M; M’) · I(A; B) Perfect decoding: M=M’ M has n. R bits of entropy Data processing

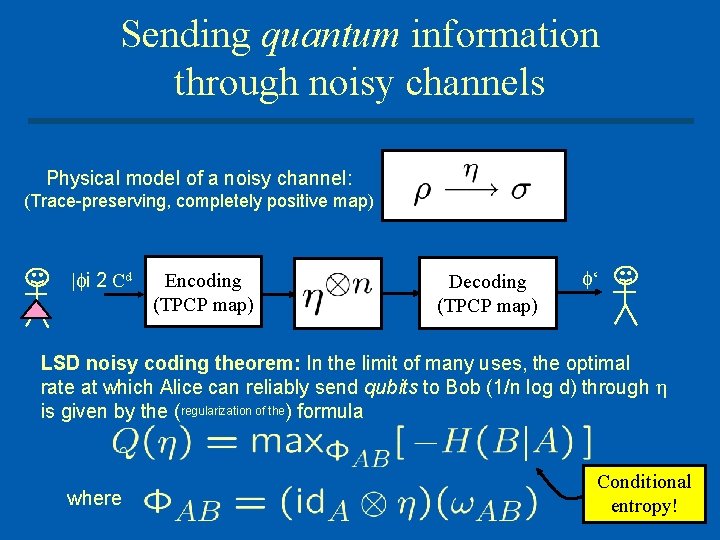
Sending quantum information through noisy channels Physical model of a noisy channel: (Trace preserving, completely positive map) | i 2 Cd Encoding (TPCP map) Decoding (TPCP map) ‘ LSD noisy coding theorem: In the limit of many uses, the optimal rate at which Alice can reliably send qubits to Bob (1/n log d) through is given by the (regularization of the) formula where Conditional entropy!

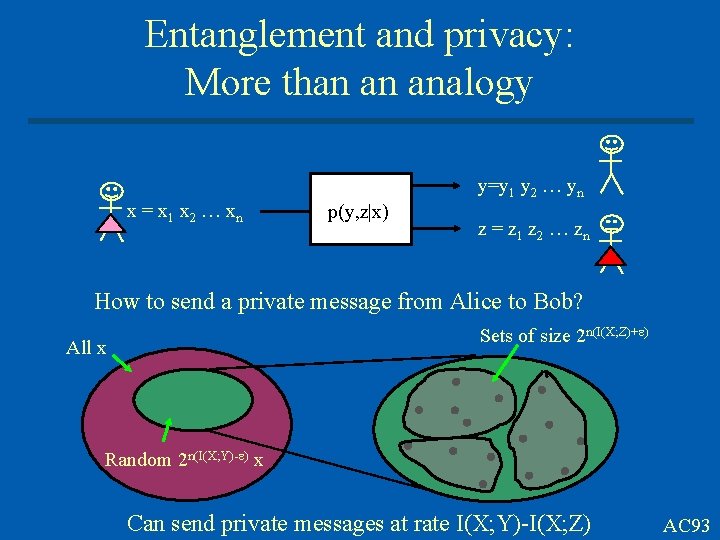
Entanglement and privacy: More than an analogy x = x 1 x 2 … xn y=y 1 y 2 … yn p(y, z|x) z = z 1 z 2 … zn How to send a private message from Alice to Bob? Sets of size 2 n(I(X; Z)+ ) All x Random 2 n(I(X; Y)- ) x Can send private messages at rate I(X; Y)-I(X; Z) AC 93

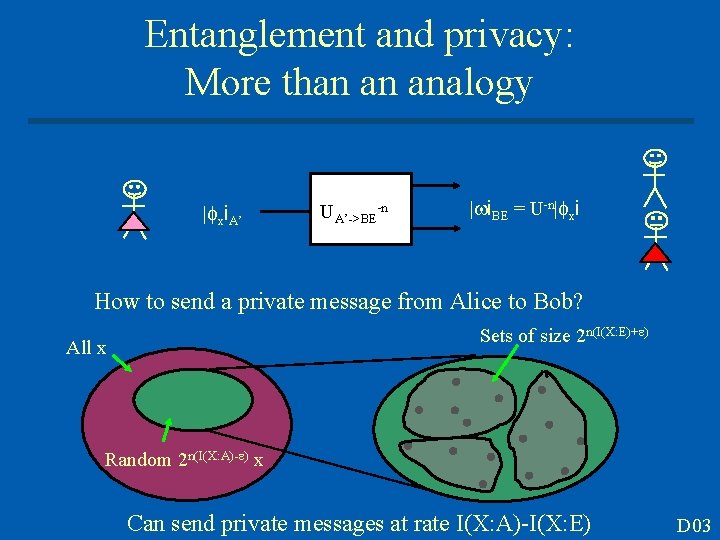
Entanglement and privacy: More than an analogy | xi. A’ UA’->BE n | i. BE = U n| xi How to send a private message from Alice to Bob? Sets of size 2 n(I(X: E)+ ) All x Random 2 n(I(X: A)- ) x Can send private messages at rate I(X: A)-I(X: E) D 03

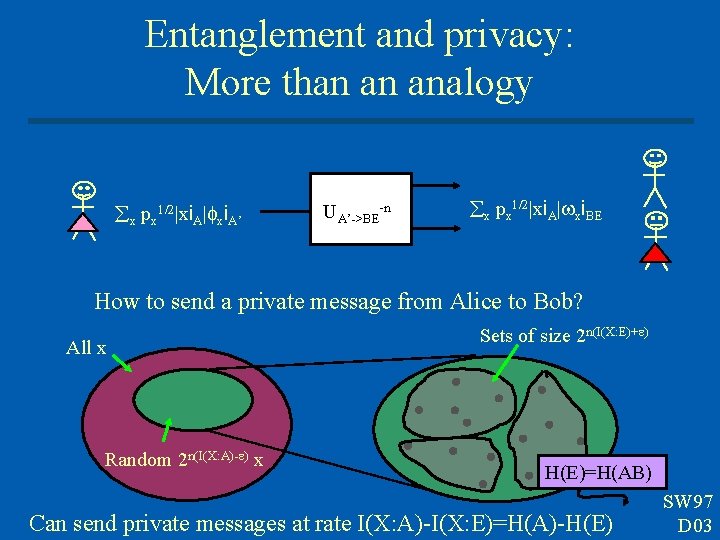
Entanglement and privacy: More than an analogy x px 1/2|xi. A| xi. A’ UA’->BE n x px 1/2|xi. A| xi. BE How to send a private message from Alice to Bob? All x Random 2 n(I(X: A)- ) x Sets of size 2 n(I(X: E)+ ) H(E)=H(AB) Can send private messages at rate I(X: A)-I(X: E)=H(A)-H(E) SW 97 D 03

Conclusions: Part I § § § Information theory can be generalized to analyze quantum information processing Yields a rich theory, surprising conceptual simplicity Operational approach to thinking about quantum mechanics: § Compression, data transmission, superdense coding, subspace transmission, teleportation

Some references: Part I: Standard textbooks: * Cover & Thomas, Elements of information theory. * Nielsen & Chuang, Quantum computation and quantum information. (and references therein) * Devetak, The private classical capacity and quantum capacity of a quantum channel, quant-ph/0304127 Part II: Papers available at arxiv. org: * Devetak, Harrow & Winter, A family of quantum protocols, quant-ph/0308044. * Horodecki, Oppenheim & Winter, Quantum information can be negative, quant-ph/0505062