Quantum dynamics in a classical phase space Anatoli

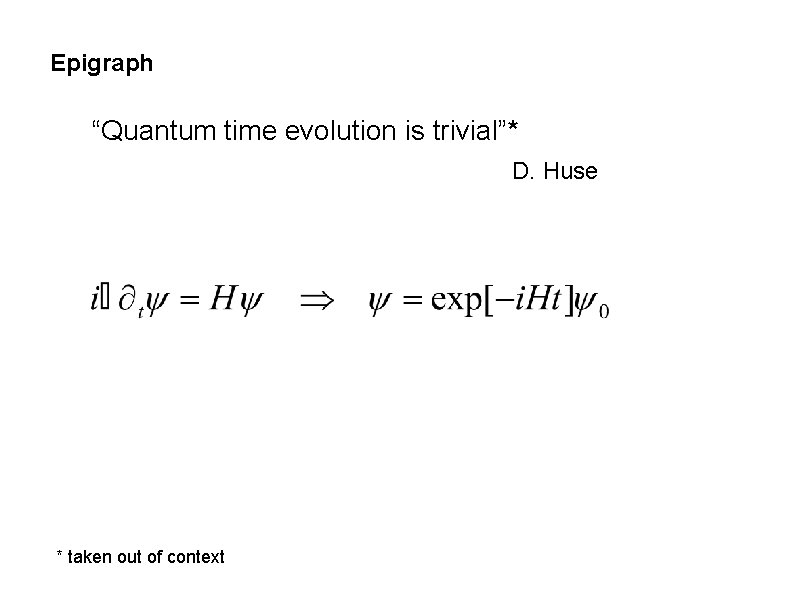
























































- Slides: 75

Quantum dynamics in a classical phase space. Anatoli Polkovnikov, Boston University ICMP 09, Mahabaleshwar, December 2009
Epigraph “Quantum time evolution is trivial”* D. Huse * taken out of context

Outline Introduction: cold atoms and quantum dynamics Quantum versus classical description of dynamics. Coherent states, duality of particle and wave classical limits. Phase space representation of quantum mechanics through the Wigner function. Weyl ordering, Moyal product, Bopp representation. Von Neumann equation for the density matrix in the Wigner representation. Semiclassical (truncated Wigner) approximation. Path integral representation of the evolution. Connection to Keldysh techniques. Causality of semiclassical description. Beyond semiclassical approximation: quantum jumps and quantum noise. Examples (cold atoms).

Literature: 1. A. P. , Representation of quantum dynamics of interacting systems through classical trajectories, ar. Xiv: 0905. 3384 2. M. A. Hillery, R. F. O'Connell, M. O. Scully, and E. P. Wigner, Distribution functions in physics: Fundamentals, Phys. Rep. , 106: 121, 1984 3. D. F. Walls and G. J. Milburn. Quantum Optics. Springer-Verlag, Berlin, 1994: C. W. Gardiner and P. Zoller. Quantum Noise. Springer-Verlag, Berlin Heidelberg, third edition, 2004. 4. M. J. Steel, M. K. Olsen, L. I. Plimak, P. D. Drummond, S. M. Tan, M. J. Collett, D. F. Walls, and R. Graham, Dynamical quantum noise in trapped Bose-Einstein condensates, Phys. Rev. A, 58: 4824, 1998. 5. P. B. Blakie, A. S. Bradley, M. J. Davis, R. J. Ballagh, and C. W. Gardiner. Dynamics and statistical mechanics of ultra-cold Bose gases using c-field techniques, Advances in Physics, 57: 363, 2008.

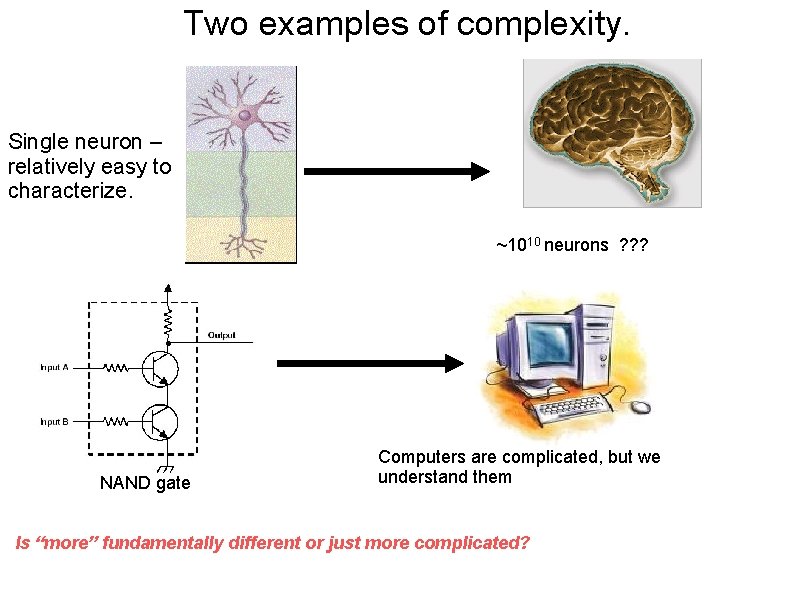
Two examples of complexity. Single neuron – relatively easy to characterize. ~1010 neurons ? ? ? NAND gate Computers are complicated, but we understand them Is “more” fundamentally different or just more complicated?

From single particle physics to many particle physics. Classical mechanics: Need to solve Newton’s equation (fully deterministic given initial conditions) Single particle Many particles Instead of one differential equation need to solve n differential equations, not a big deal!? The only uncertainty comes from potentially unknown initial conditions. Chaos impedes our ability to make long time accurate deterministic predictions.

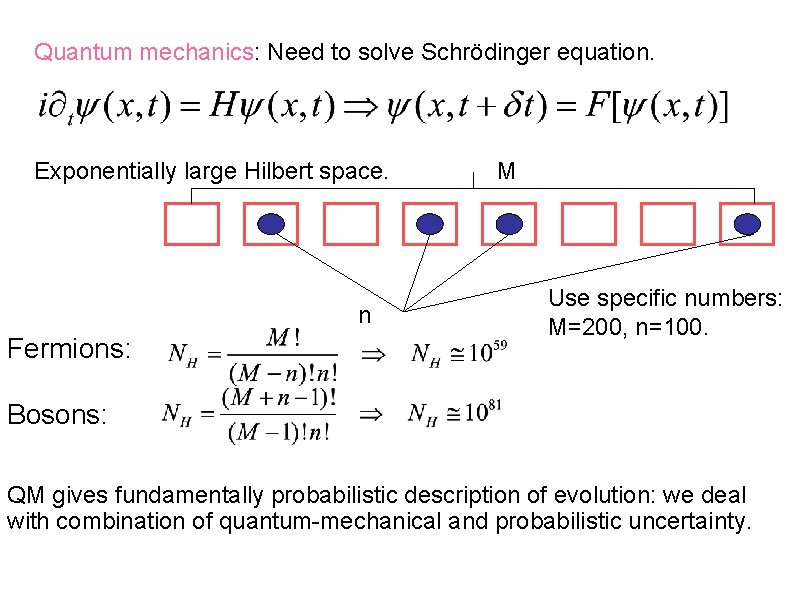
Quantum mechanics: Need to solve Schrödinger equation. Exponentially large Hilbert space. n Fermions: M Use specific numbers: M=200, n=100. Bosons: QM gives fundamentally probabilistic description of evolution: we deal with combination of quantum-mechanical and probabilistic uncertainty.

Dynamics Quantum systems: time evolution is trivial, complexity (chaos) is hidden in the many-body eigenstates and in exponentially large Hilbert space. Classical systems: states of the system are trivial (points in the phase space), time evolution is nontrivial.

Experiments: best simulators are real systems. Problem with solid state (liquid) systems – Hamiltonians are two complex Cold atoms: (controlled and tunable Hamiltonians, isolation from environment) 1. Equilibrium thermodynamics: Quantum simulations of equilibrium condensed matter systems Experimental examples:

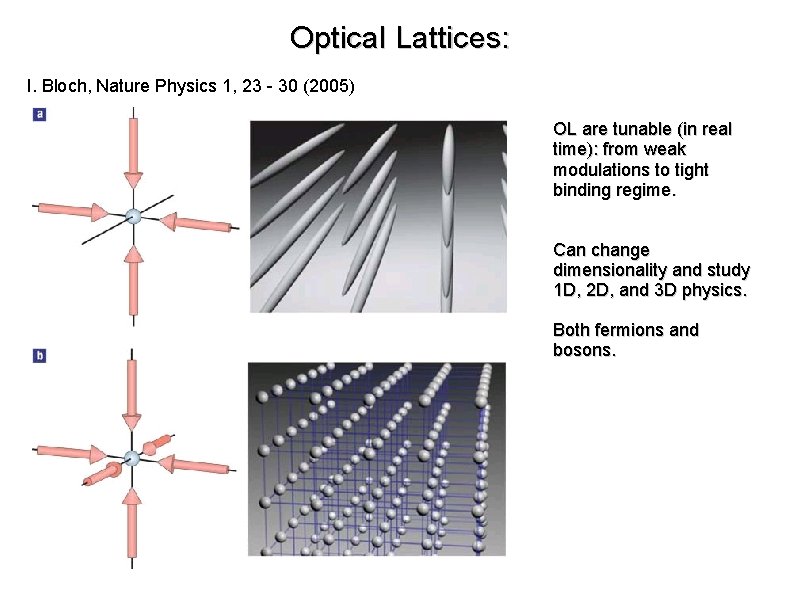
Optical Lattices: I. Bloch, Nature Physics 1, 23 - 30 (2005) OL are tunable (in real time): from weak modulations to tight binding regime. Can change dimensionality and study 1 D, 2 D, and 3 D physics. Both fermions and bosons.

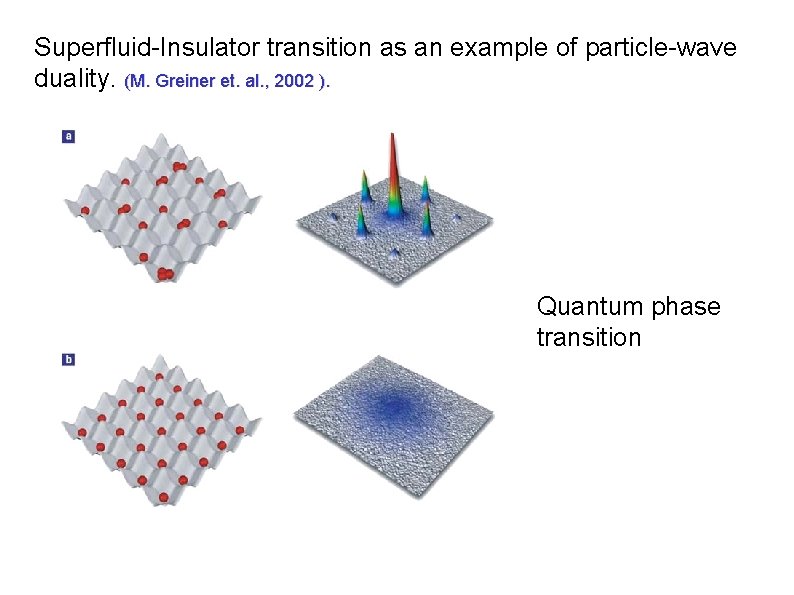
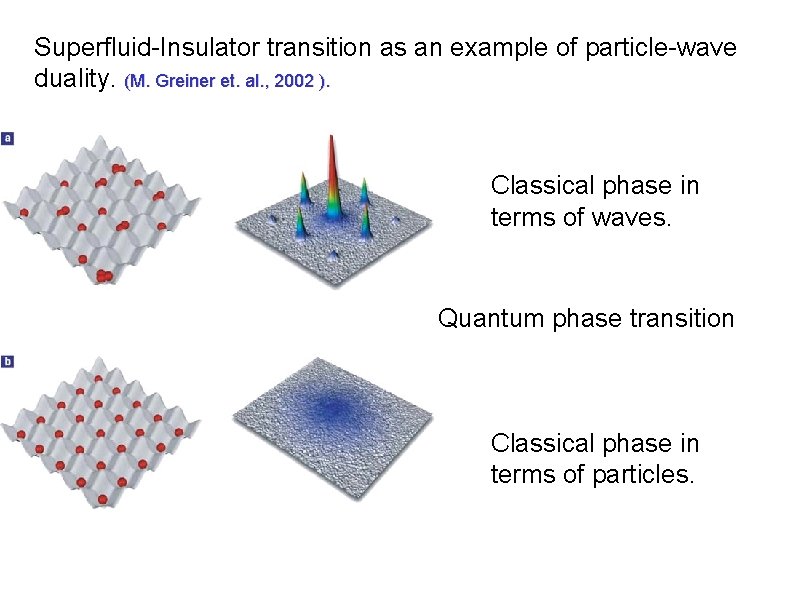
Superfluid-Insulator transition as an example of particle-wave duality. (M. Greiner et. al. , 2002 ). Quantum phase transition

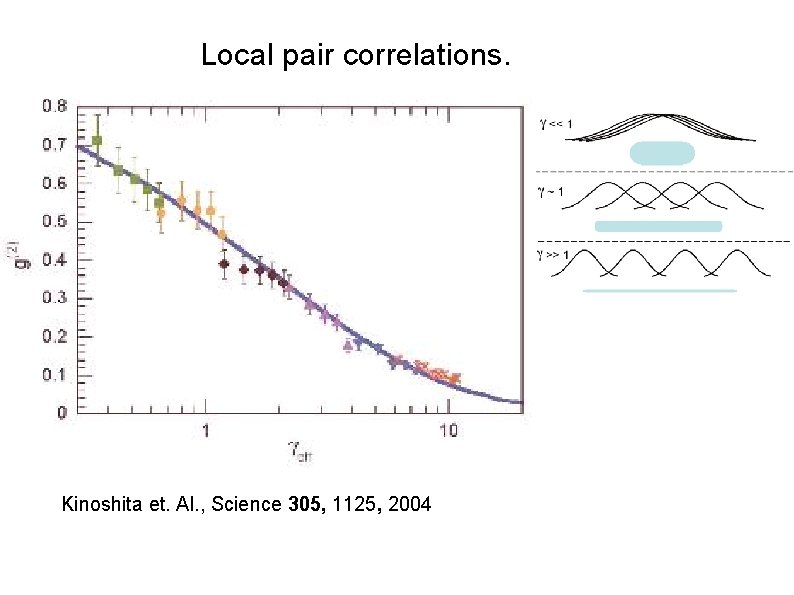
Repulsive Bose gas. Lieb-Liniger, complete solution 1963. M. Olshanii, 1998 interaction parameter Experiments: T. Kinoshita, T. Wenger, D. S. Weiss. , Science 305, 1125, 2004 Also, B. Paredes 1, A. Widera, V. Murg, O. Mandel, S. Fölling, I. Cirac, G. V. Shlyapnikov, T. W. Hänsch and I. Bloch, Nature 277 , 429 (2004)

Local pair correlations. Kinoshita et. Al. , Science 305, 1125, 2004

Cold atoms: (controlled and tunable Hamiltonians, isolation from environment) 1. Equilibrium thermodynamics: Quantum simulations of equilibrium condensed matter systems 2. Quantum dynamics: Coherent and incoherent dynamics, integrability, quantum chaos, …


In the continuum this system is equivalent to an integrable Kd. V equation. The solution splits into non-thermalizing solitons Kruskal and Zabusky (1965 ).

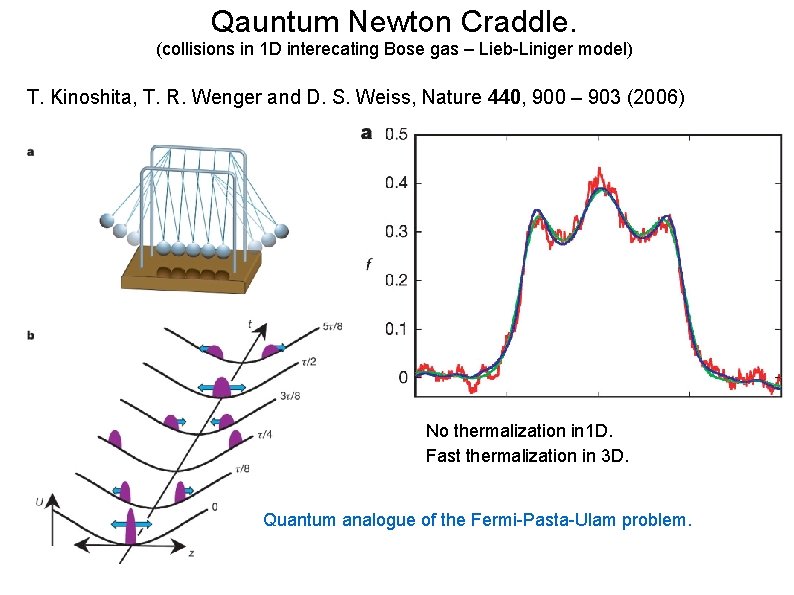
Qauntum Newton Craddle. (collisions in 1 D interecating Bose gas – Lieb-Liniger model) T. Kinoshita, T. R. Wenger and D. S. Weiss, Nature 440, 900 – 903 (2006) No thermalization in 1 D. Fast thermalization in 3 D. Quantum analogue of the Fermi-Pasta-Ulam problem.

Sudden quench M. Greiner, O. Mandel, T. W. Hänsch and I. Bloch, Nature 419, 51 -54, 2002

Expansion of quantum dynamics around classical limit. Classical (saddle point) limit: (i) Newtonian equations for particles, (ii) Gross-Pitaevskii equations for matter waves, (iii) Maxwell equations for classical e/m waves and charged particles, (iv) Bloch equations for classical rotators, etc. Questions: What shall we do with equations of motion? What shall we do with initial conditions? What shall we do with observables? Challenge : How to reconcile the exponential complexity of quantum many body systems and power law complexity of classical systems?

Coherent states. Dual classical corpuscular and wave limits. Bosonic creation-annihilation operators Classical limit: Basic representation: coherent states: Coordinate-momentum representation

Poisson Brackets and Equations of Motion Introduce As in the coordinate momentum representation in the classical limit

Equations of motion for operators Classical limit Recover Gross-Pitaevskii equation – classical wave equation for interacting bosons

Hamiltonian dynamics. Particle limit Wave limit Newton’s equations GP equations Phase space operators Canonical commutation relations Classical limit Poisson brackets Classical limit – Equations of motion

Superfluid-Insulator transition as an example of particle-wave duality. (M. Greiner et. al. , 2002 ). Classical phase in terms of waves. Quantum phase transition Classical phase in terms of particles.

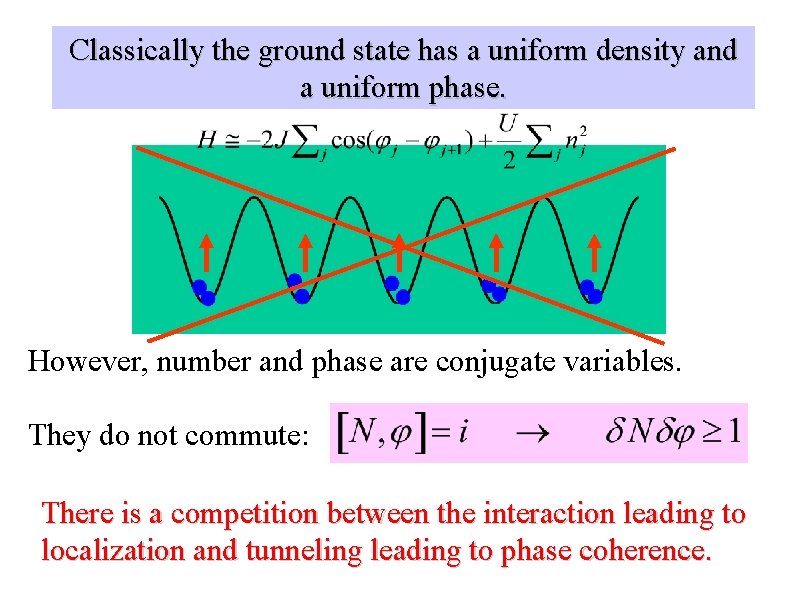
Classically the ground state has a uniform density and a uniform phase. However, number and phase are conjugate variables. They do not commute: There is a competition between the interaction leading to localization and tunneling leading to phase coherence.

How can we connect classical and quantum description? Wigner function and Weyl ordering. G. S. of a harmonic oscillator: Wigner function can be interpreted as a quasi probability distribution.

Wigner function is the Weyl symbol of the density matrix Facts about the Wigner function 1. Wigner function is analogous to the probability distribution. 2. is not positive-definite – quasi-probability dsitribution. 3. At finite T Wigner function becomes Bolzmann’s function – smooth connection of quantum and classical statistics.

Example: Harmonic oscillator:

Expectation value of product of operators, Moyal product. 0 - Moyal product becomes ordinary product


The Bopp representation of an operator reduces it to the classical function in the limit 0 and automatically reproduces the Weyl symbols of these operator.

Consider a coherent state as an example


Bopp operators for coherent states

Summary of phase space methods Wigner-Weyl quantization: Moyal product (basic multiplication rule) Bopp operators (basic representation)

Phase space methods and quantum dynamics Von Neumann equation for the density matrix Coherent states:

Expansion in This equation can be solved using the method of characteristics, which are the classical trajectories.


Coherent states: Characteristics: W( , *, t)=const are given by the Gross-Pitaevskii equation Example

Semiclassical (truncated Wigner) approximation Quantum mechanics enters through 1. The Wigner function, which is different from the Boltzmann’s distribution, and which can be nonpositive. 2. Through the Weyl ordering of the Hamiltonian in the classical equations of motion. 3. Through the Weyl ordering of the observable Coherent states – same story:

Interpret this derivative as a response to the quantum jump

Combining left and right Bopp representations we find The last rule generalizes canonical commutation relations to non-equal times



Sketch of the path integral derivation of the time evolution. (Very similar to Keldysh formalism) Change variables

Wigner function and Weyl oredring emerg automatically from the boundary terms at = 0 and =t. No special assumptions are needed. For details of the derivation see: A. P. ar. Xiv: 0905. 3384, Phys. Rev. A, vol. 68 (5), 053604 (2003).

Coherent state representation: Same idea but now insert coherent states Is the classical Gross-Pitaevskii field, is the quantum field.

Recover semiclassical approximation by expanding action to the linear order in quantum fields: Then functional integration is trivial: we are getting -function constraints enforcing classical equations of motion:

Once again semiclassical – truncated Wigner – approximation The same story happens in the coherent state basis: integrating over the quantum field in the leading order enforces Gross. Pitaevskii equations on the classical fileds:

Non-equal time correlations functions (result) Operator dependent jump at t=t 1 Recover Bopp operators (also automatically). Same for coherent states.

Beyond truncated Wigner approximation (TWA) Expand action to the third order in quantum fields (no corrections to TWA in harmonic theories)

Note that plays the role of the correction to the conjugate momentum = quantum jump Higher order corrections – more jumps

Quantum corrections emerge as a nonlinear response to infinitesimal jumps in classical phase space variables. Each jump carries a factor of 2. Jumps do not affect short time behavior, i. e. TWA is asymptotically exact at short times. Equivalent representation through stochastic quantum jumps

Coherent states. Same story Bose Hubbard model

Examples Classical equations of motion


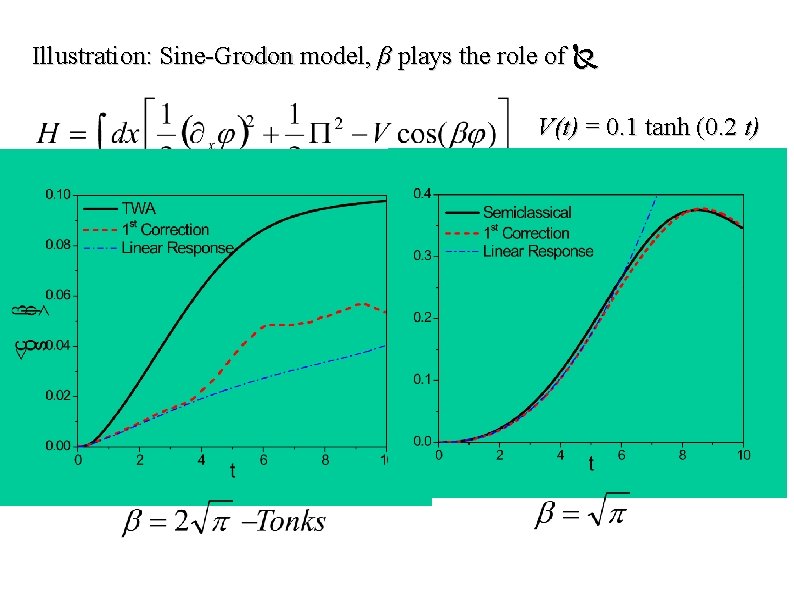
More complicated example: sine-Gordon (Frenkel-Kontorova) model Assume initially V=0 and the system is in the ground state

Illustration: Sine-Grodon model, β plays the role of V(t) = 0. 1 tanh (0. 2 t)

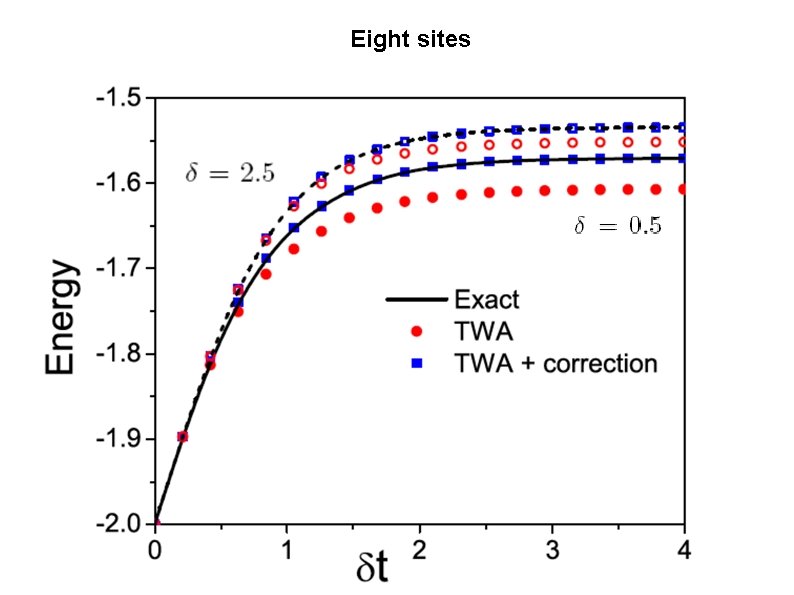
Turning on interactions in a system of interacting bosons Choose N=1 (per site), J=1, U 0=1. Follow energy in the system.

Eight sites

2 D lattice 32 x 32 sites

Decoupling two 2 D superfluids (with L. Mathey)

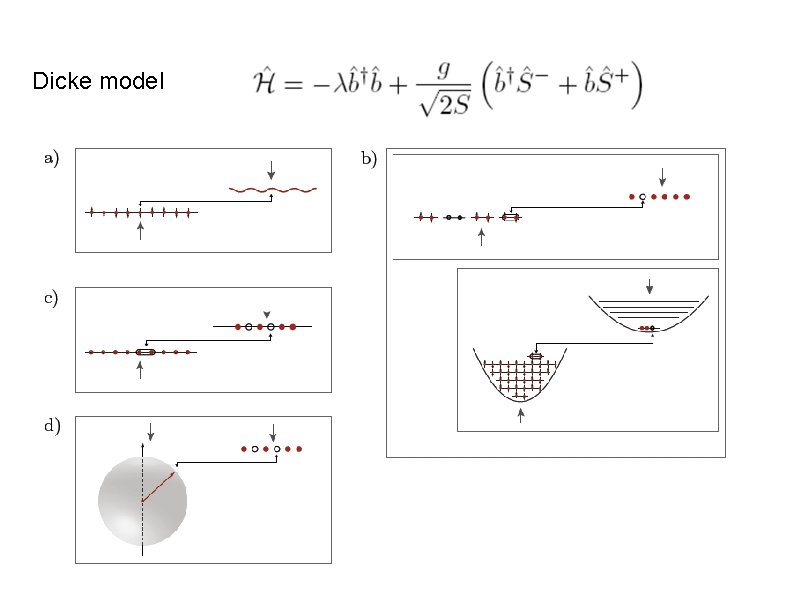
Dicke model

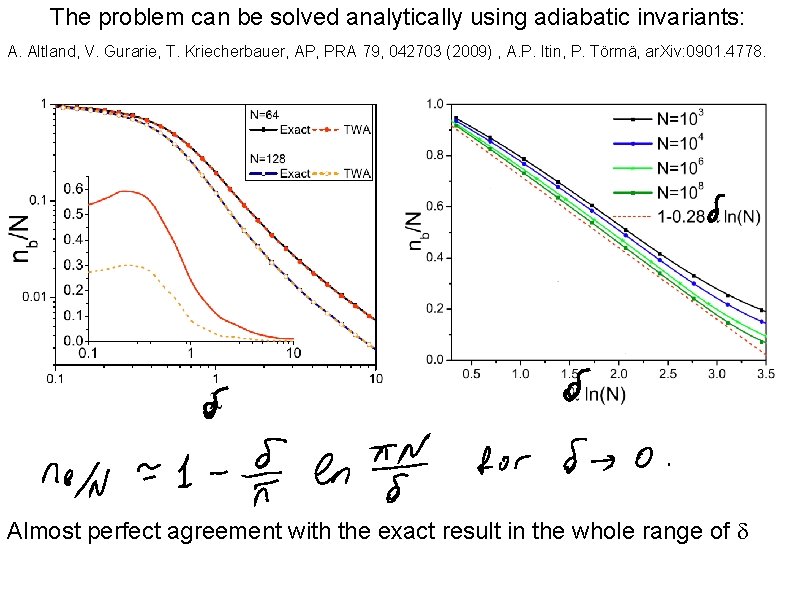
Dicke model (many-level Landau-Zener problem) Consider (t)=- t. Start in the with spin pointing up and no bosons. Classical limit: have exact solution b(t)=0, Sz(t)=S, Sx(t)=Sy(t)=0. Quantum mechanically expect that at 0 – adiabatically follow the ground state:

The problem can be solved analytically using adiabatic invariants: A. Altland, V. Gurarie, T. Kriecherbauer, AP, PRA 79, 042703 (2009) , A. P. Itin, P. Törmä, ar. Xiv: 0901. 4778. Almost perfect agreement with the exact result in the whole range of

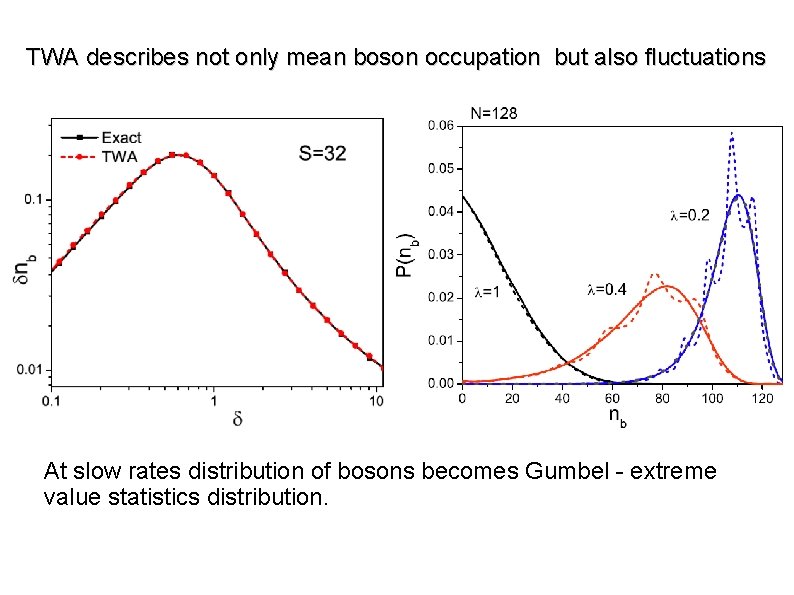
TWA describes not only mean boson occupation but also fluctuations At slow rates distribution of bosons becomes Gumbel - extreme value statistics distribution.

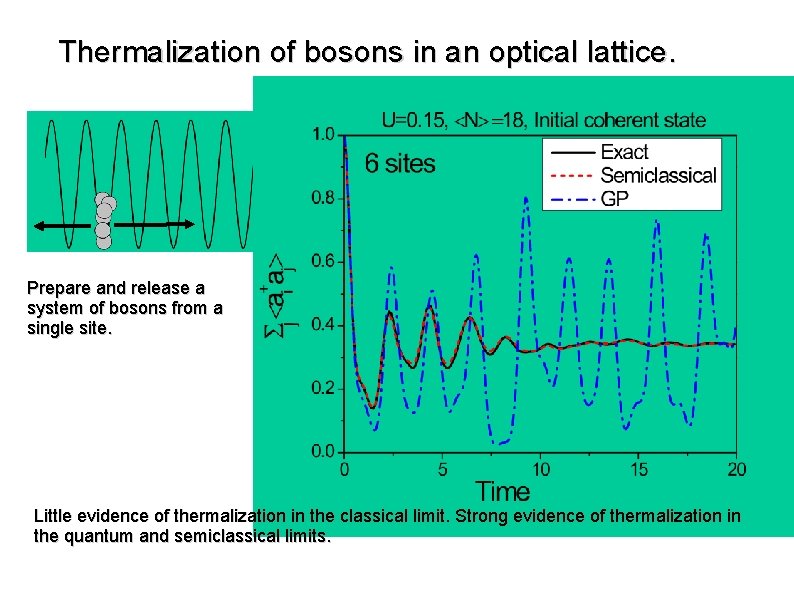
Thermalization of bosons in an optical lattice. Prepare and release a system of bosons from a single site. Little evidence of thermalization in the classical limit. Strong evidence of thermalization in the quantum and semiclassical limits.

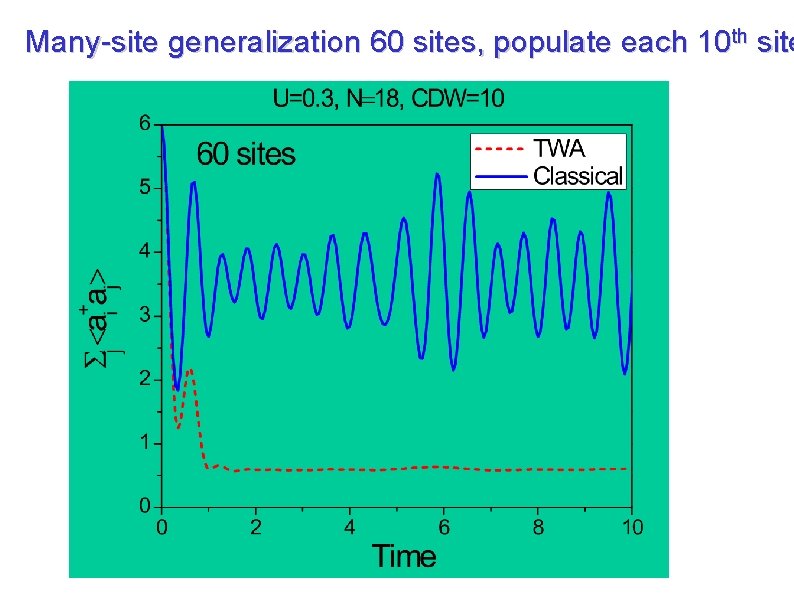
Many-site generalization 60 sites, populate each 10 th site

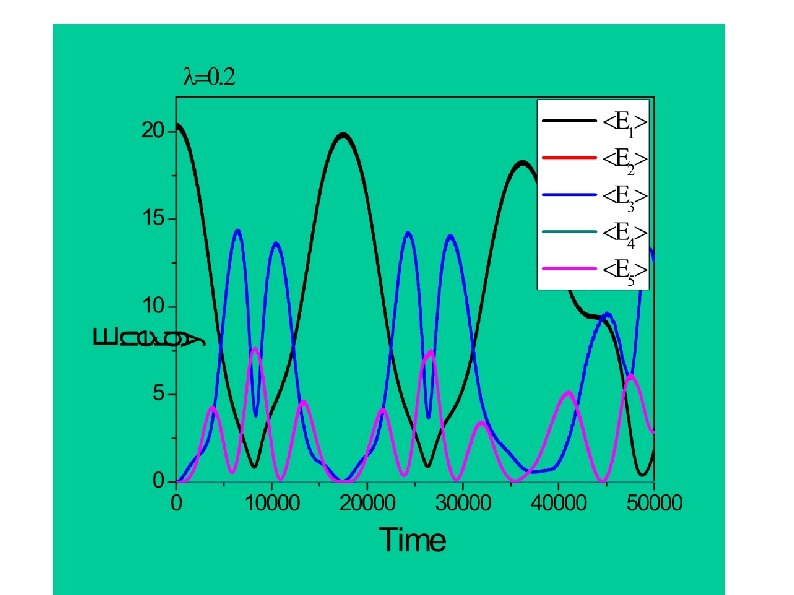
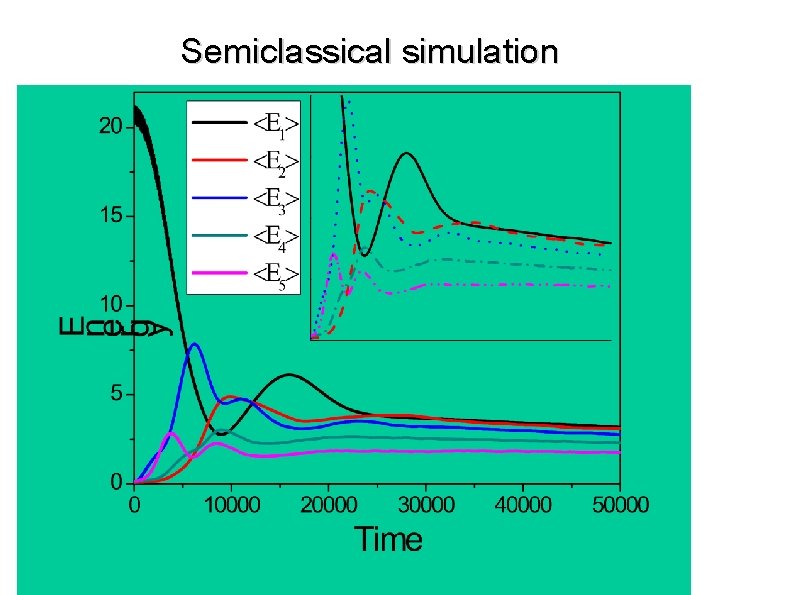
Final Example (back to FPU problem). with V. Oganesyan, I. Danshita, R. Hipolito m = 10, = 1, = 0. 2, L = 100 Choose initial state corresponding to initial displacement at wave vector k = 2 /L (first excited mode). Follow the energy in the first excited mode as a function of time. Cold atom analogue – quantum rotor model

Classical simulation

Semiclassical simulation


Key points: 1) Hamiltonian dynamics. Particle limit Wave limit Newton’s equations GP equations Phase space operators Canonical commutation relations Classical limit Poisson brackets Classical limit – Equations of motion

2) Phase space representation of QM (naturally emerges from Feynman path interal) Wigner-Weyl quantization: Bopp operators: generate Weyl symbol. Provide natural interpretation of commutation relations through jumps in the classical phase space

3) Representation of quantum dynamics. Semiclassical approximation: Quantum corrections: nonlinear response or stochastic quantum jumps with non-positive probability. These methods are very useful to analyze various quantum (coherent) dynamical problems with initial conditions. Many applications to cold atoms. Open new possibilities.
 Bugorski photos
Bugorski photos Anatoli polkovnikov
Anatoli polkovnikov Anatoli frishman
Anatoli frishman Anatoli chitov
Anatoli chitov Quantum physics vs quantum mechanics
Quantum physics vs quantum mechanics Quantum physics vs quantum mechanics
Quantum physics vs quantum mechanics Subir sachdev quantum phase transitions
Subir sachdev quantum phase transitions 物性理論
物性理論 Normal phase vs reverse phase chromatography
Normal phase vs reverse phase chromatography Hplc reverse phase vs normal phase
Hplc reverse phase vs normal phase Mobile phase and stationary phase
Mobile phase and stationary phase Stationary phase and mobile phase in hplc
Stationary phase and mobile phase in hplc Normal phase vs reverse phase chromatography
Normal phase vs reverse phase chromatography Power formula three phase
Power formula three phase Which detector used in hplc
Which detector used in hplc Phase to phase voltage
Phase to phase voltage Broad phase vs narrow phase
Broad phase vs narrow phase Phase space
Phase space Phase space
Phase space Phase space
Phase space Joint space vs cartesian space
Joint space vs cartesian space Space junk the space age began
Space junk the space age began Camera space to world space
Camera space to world space Cartesian space vs joint space
Cartesian space vs joint space Ndc to screen space
Ndc to screen space What is time
What is time Expectation value of hermitian operator
Expectation value of hermitian operator D orbital shape
D orbital shape Expectation value of energy in quantum mechanics
Expectation value of energy in quantum mechanics Quantum and nuclear physics
Quantum and nuclear physics Eft memory
Eft memory Incident wave equation
Incident wave equation Expectation value in quantum mechanics
Expectation value in quantum mechanics Quantum mechanical model
Quantum mechanical model Gil kalai quantum
Gil kalai quantum The limits of quantum computers
The limits of quantum computers Turing test
Turing test Bohr quantum mechanical model
Bohr quantum mechanical model Quantum numbers and electron configuration
Quantum numbers and electron configuration Gil kalai quantum computing
Gil kalai quantum computing Quantum mechanical model labeled
Quantum mechanical model labeled Quantum network simulator
Quantum network simulator French and taylor quantum mechanics
French and taylor quantum mechanics Zeno paradox of motion
Zeno paradox of motion Quantum vs quantity
Quantum vs quantity Valdis šteins
Valdis šteins Quantum statistics
Quantum statistics Quantum parallelism
Quantum parallelism Spin quantum number of nitrogen
Spin quantum number of nitrogen Magnetic quantum number
Magnetic quantum number D orbital magnetic quantum number
D orbital magnetic quantum number Quantum numbers
Quantum numbers Quantum mechanics in your face
Quantum mechanics in your face Quantum wave equation
Quantum wave equation Quantum mechanical atom model
Quantum mechanical atom model Quantum mechanical model definition chemistry
Quantum mechanical model definition chemistry Quantum mechanical model definition
Quantum mechanical model definition What is the electron configuration of 24cr4+?
What is the electron configuration of 24cr4+? Modern quantum mechanical model
Modern quantum mechanical model Quantum information stephen m. barnett
Quantum information stephen m. barnett Gabriela barreto lemos
Gabriela barreto lemos Global quantum healing
Global quantum healing Quantum espresso parallelization
Quantum espresso parallelization Quantum yield formula
Quantum yield formula Quantum binary
Quantum binary Quantum mechanics postulate
Quantum mechanics postulate Quantum discord
Quantum discord Quantum physics wave function
Quantum physics wave function Postulates of quantum mechanics
Postulates of quantum mechanics Spin 1 operators
Spin 1 operators Operators in quantum mechanics
Operators in quantum mechanics Prime factorization quantum algorithm
Prime factorization quantum algorithm Quantum numbers khan academy
Quantum numbers khan academy Quantum number of silicon
Quantum number of silicon Random simulation generator
Random simulation generator Quantum mechanics
Quantum mechanics