Quantum Cryptography Post Tenebras Lux Grgoire Ribordy Outline

Quantum Cryptography Post Tenebras Lux! Grégoire Ribordy

Outline q Introduction: Cryptography q Quantum Information Processing q Quantum cryptography protocole q Practical system q Applications and outlook www. idquantique. com

Cryptography Eve Document Secure communication Key Decryption Encryption Alice Bob Key transmission Key generation www. idquantique. com
Secret key cryptography q Encryption and decryption key identical q Problem: Key exchange q The longer the key, the higher the security – One-time pad www. idquantique. com
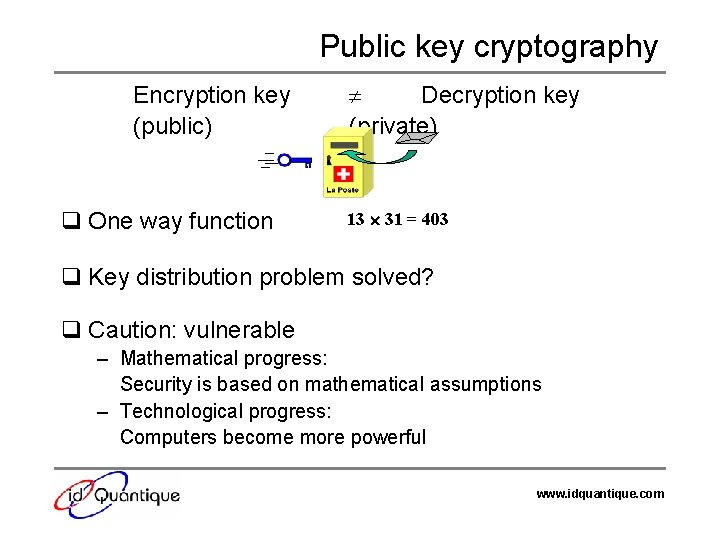
Public key cryptography Encryption key (public) q One way function Decryption key (private) 13 31 = 403 q Key distribution problem solved? q Caution: vulnerable – Mathematical progress: Security is based on mathematical assumptions – Technological progress: Computers become more powerful www. idquantique. com
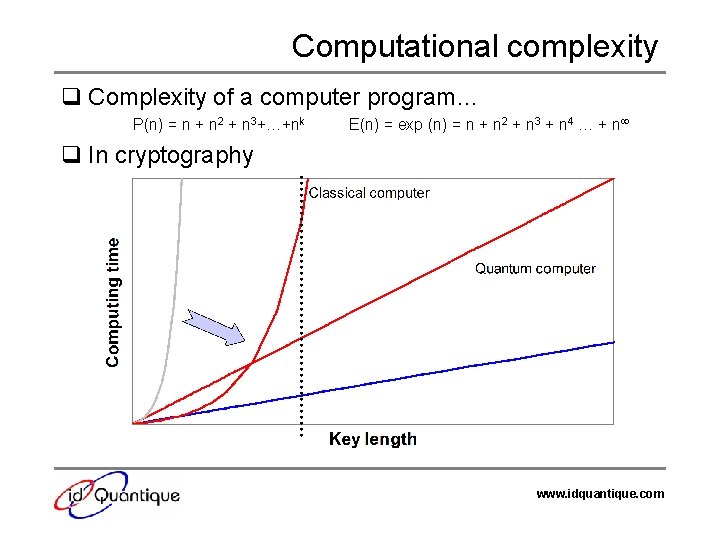
Computational complexity q Complexity of a computer program… P(n) = n + n 2 + n 3+…+nk E(n) = exp (n) = n + n 2 + n 3 + n 4 … + n q In cryptography www. idquantique. com
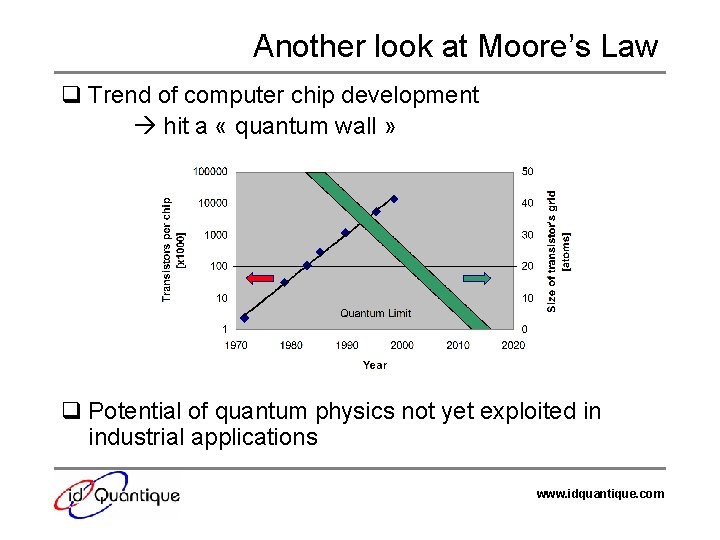
Another look at Moore’s Law q Trend of computer chip development hit a « quantum wall » q Potential of quantum physics not yet exploited in industrial applications www. idquantique. com
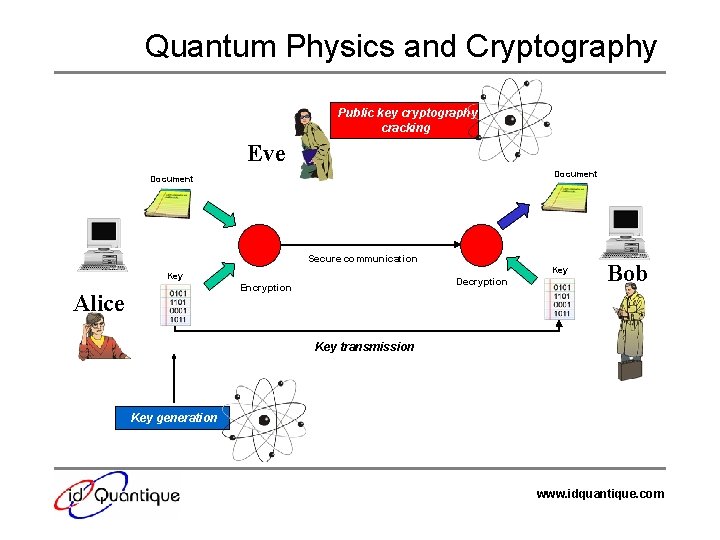
Quantum Physics and Cryptography Public key cryptography cracking Eve Document Secure communication Key Decryption Encryption Alice Bob Key transmission Key generation www. idquantique. com

Quantum Random Number Generator q Physical randomness source q Commercially available q Applications – Cryptography – Numerical simulations – Statistics www. idquantique. com
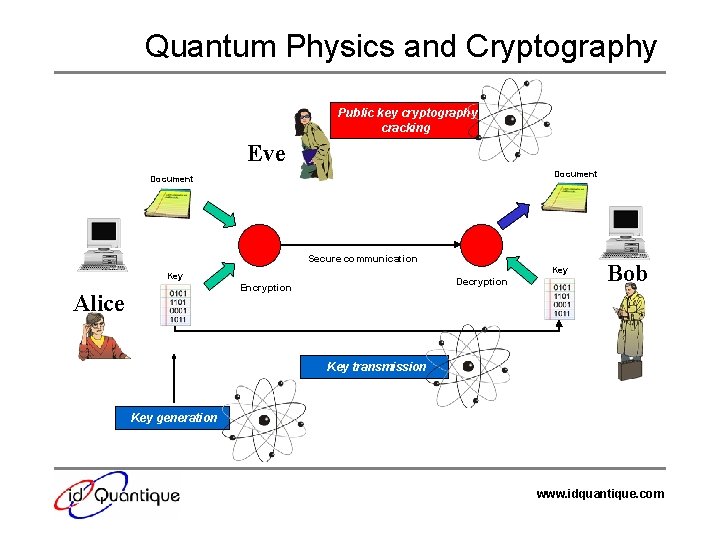
Quantum Physics and Cryptography Public key cryptography cracking Eve Document Secure communication Key Decryption Encryption Alice Bob Key transmission Key generation www. idquantique. com
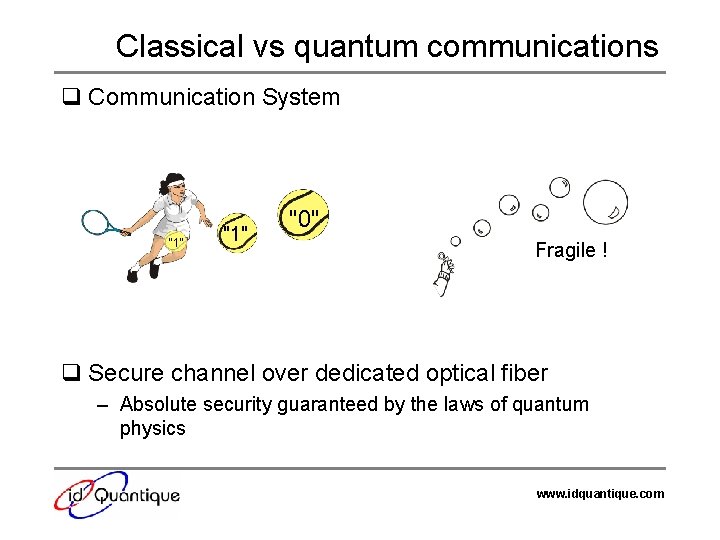
Classical vs quantum communications q Communication System "1" "0" Fragile ! q Secure channel over dedicated optical fiber – Absolute security guaranteed by the laws of quantum physics www. idquantique. com
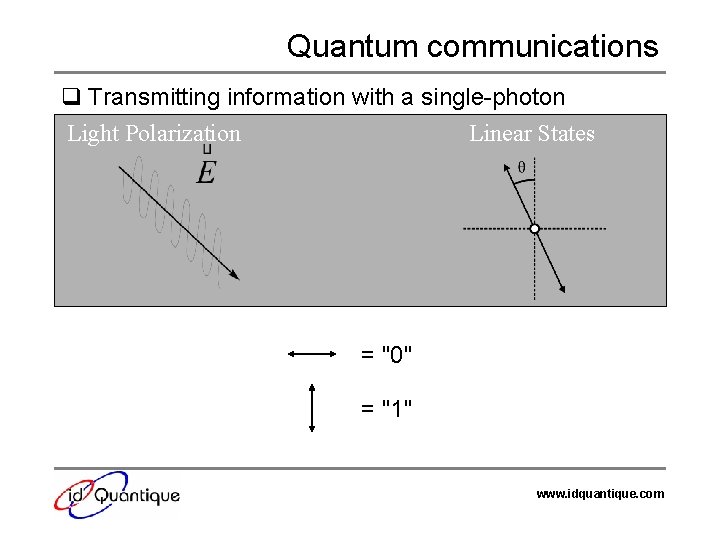
Quantum communications q Transmitting information with a single-photon Light Polarization Linear States = "0" = "1" www. idquantique. com

Eavesdropping (1) q A single-photon constitutes an elementary quantum system It cannot be split q Semi-transparent mirror 50% www. idquantique. com

Eavesdropping (2) q Communication interception Alice Bob "0" Eve q Use quantum physics to force spy to introduce errors in the communication www. idquantique. com
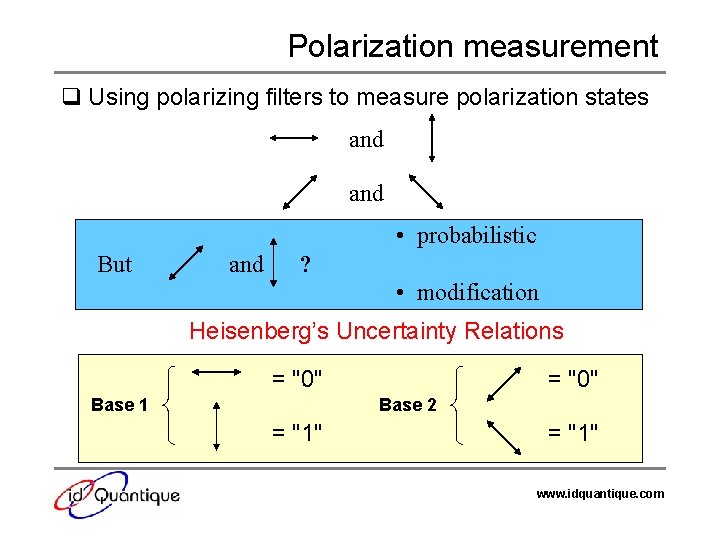
Polarization measurement q Using polarizing filters to measure polarization states and • probabilistic But and ? • modification Heisenberg’s Uncertainty Relations = "0" Base 1 = "0" Base 2 = "1" www. idquantique. com

Quantum Cryptography Protocole q BB 84 q A better name: Quantum Key Distribution www. idquantique. com
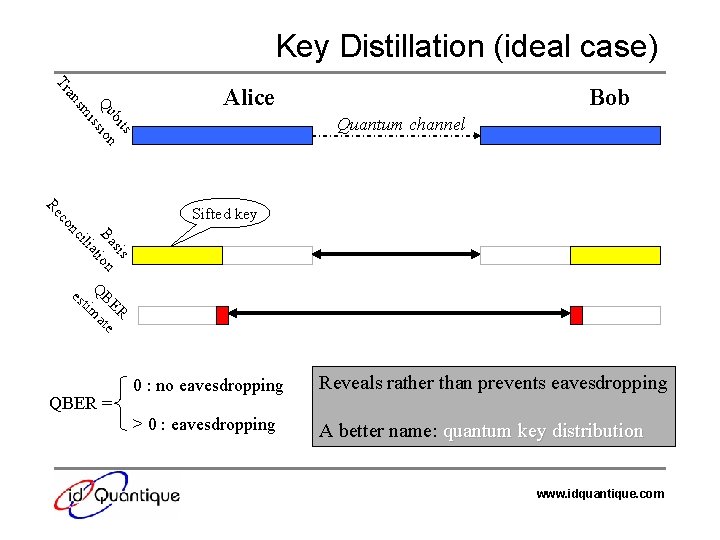
Key Distillation (ideal case) Tr s bit Qu sion is sm an Alice Bob Quantum channel sis Ba tion a ili nc co Re Sifted key es QB tim ER at e QBER = 0 : no eavesdropping Reveals rather than prevents eavesdropping > 0 : eavesdropping A better name: quantum key distribution www. idquantique. com
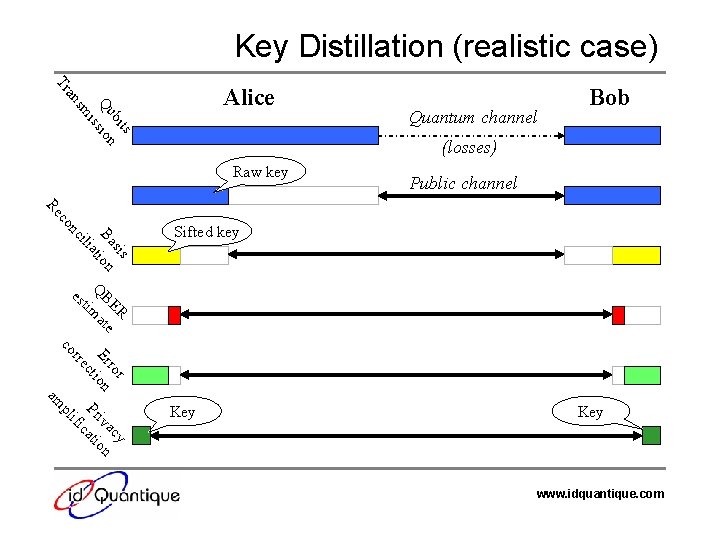
Key Distillation (realistic case) Tr s bit Qu sion is sm an Alice Quantum channel Bob (losses) Raw key Public channel sis Ba tion a ili nc co Re Sifted key es QB tim ER at e rre r ro Er on cti co pl y ac iv on Pr cati ifi am Key www. idquantique. com
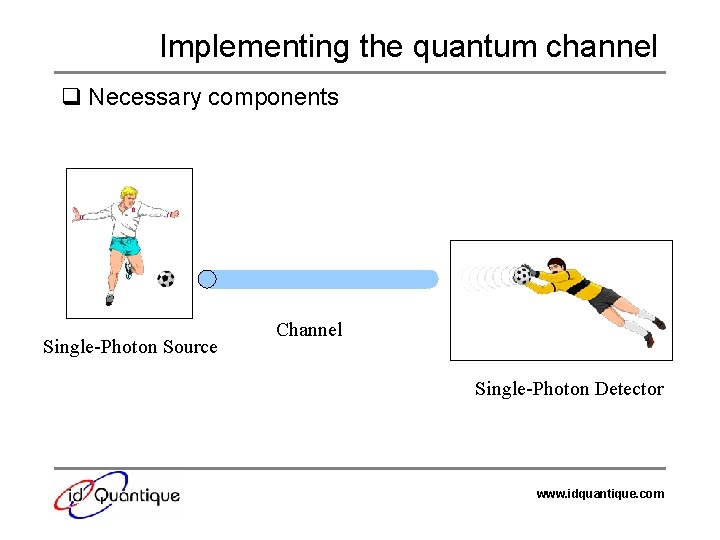
Implementing the quantum channel q Necessary components Single-Photon Source Channel Single-Photon Detector www. idquantique. com

Quantum Cryptography System • Collaboration: id Quantique – Uni. Ge • Pilot tests in 2003 www. idquantique. com
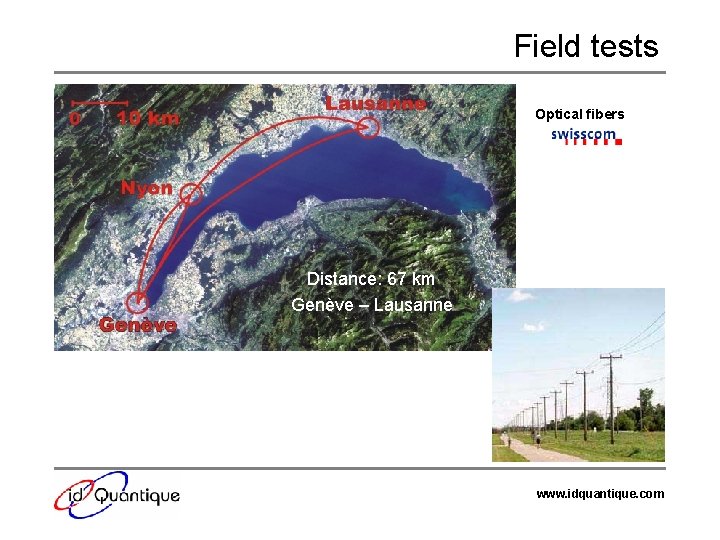
Field tests Optical fibers Distance: 67 km Genève – Lausanne www. idquantique. com
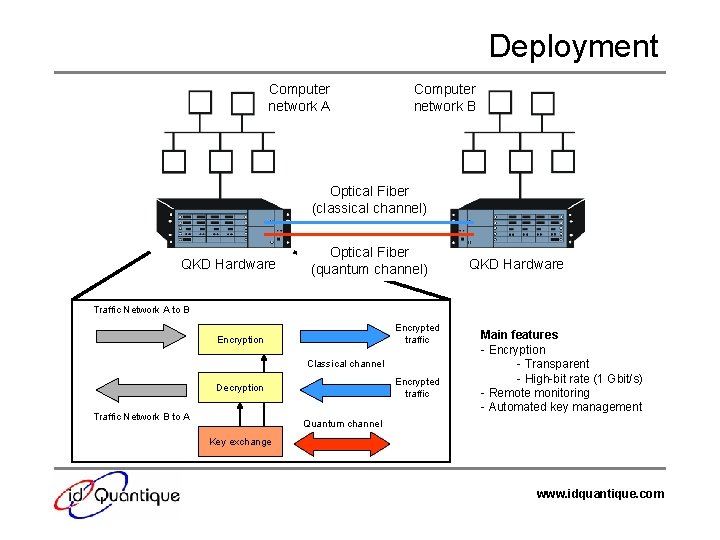
Deployment Computer network A Computer network B Optical Fiber (classical channel) QKD Hardware Optical Fiber (quantum channel) QKD Hardware Traffic Network A to B Encrypted traffic Encryption Classical channel Encrypted traffic Decryption Traffic Network B to A Main features - Encryption - Transparent - High-bit rate (1 Gbit/s) - Remote monitoring - Automated key management Quantum channel Key exchange www. idquantique. com

Applications q Advantages – Automated key management – Long term security q Constraints – Optical fiber – Distance < 100 km q High-security applications in a metropolitan area network – Financial sector, e-government – Storage, disaster recovery www. idquantique. com

Extending the distance q Secure relays q Improved components – Photon counting detectors – Photonic crystal fibers: 0. 2 d. B/km 0. 02 d. B/km q Quantum repeater q Free-space links to satellites www. idquantique. com
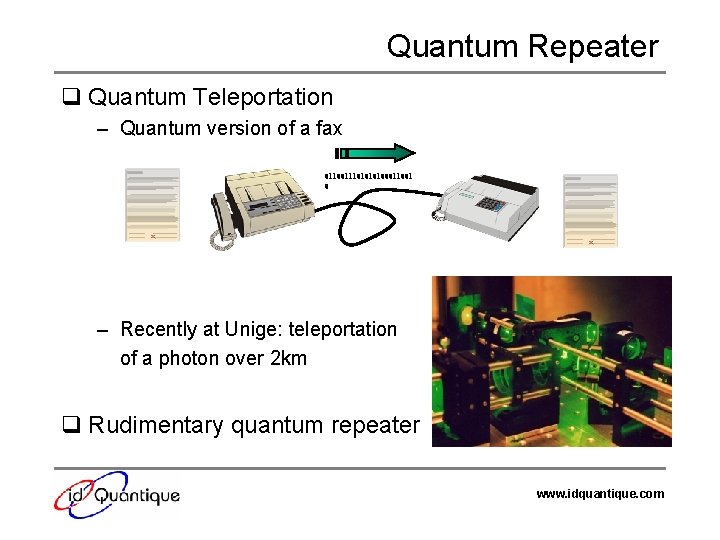
Quantum Repeater q Quantum Teleportation – Quantum version of a fax 011001110100011001 0 – Recently at Unige: teleportation of a photon over 2 km q Rudimentary quantum repeater www. idquantique. com
Free-space QKD q Satellites = secure relay Tokyo Genève q Experiments over horizontal links – 23. 4 km in the German Alps www. idquantique. com

Post Tenebras Lux? www. idquantique. com

Thank you for your attention id Quantique SA Chemin de la Marbrerie, 3 CH-1227 Carouge / Geneva Switzerland Ph: +41 22 301 83 71 Fax: +41 22 301 83 79 info@idquantique. com www. idquantique. com
- Slides: 28