Quantum Counterfeit Coin Problems Kazuo Iwama Kyoto Univ

Quantum Counterfeit Coin Problems Kazuo Iwama (Kyoto Univ. ) Harumichi Nishimura (Osaka Pref. Univ. ) Rudy Raymond (IBM Research - Tokyo) Junichi Teruyama (Kyoto Univ. ) ISAAC 2010, Dec. 15, 2010, Jeju (Korea)

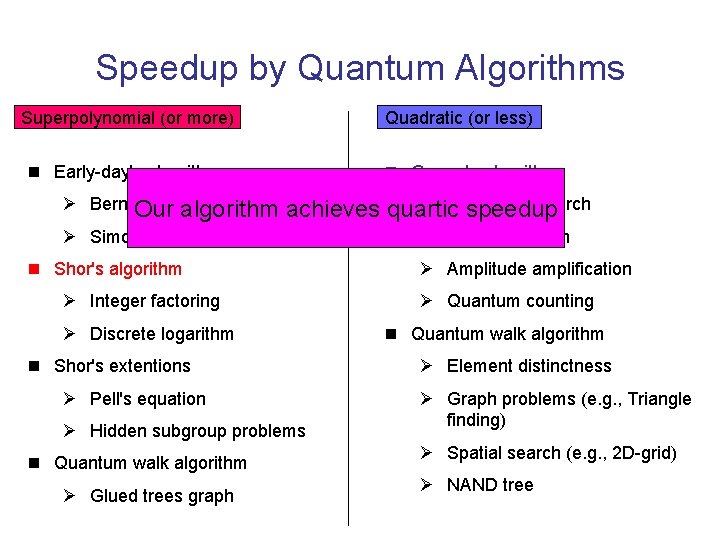
Speedup by Quantum Algorithms Superpolynomial (or more) Quadratic (or less) n Early-day's algorithm Ø Bernstein-Vazirani Our algorithm n Grover's algorithm Ø Unordered search achieves quartic speedup Ø Simon n Shor's algorithm Ø Integer factoring Ø Discrete logarithm n Shor's extentions Ø Pell's equation Ø Hidden subgroup problems n Quantum walk algorithm Ø Glued trees graph n Grover's application Ø Amplitude amplification Ø Quantum counting n Quantum walk algorithm Ø Element distinctness Ø Graph problems (e. g. , Triangle finding) Ø Spatial search (e. g. , 2 D-grid) Ø NAND tree

Counterfeit Coin Problem The counterfeit coin problem is a well-known puzzle. You have eight similar coins and a beam balance. At most one coin is counterfeit and hence underweight. How can you detect whethere is an underweight coin, and if so, which one, using the balance only twice? [E. Schell, American Mathematical Monthly 52, p. 46, 1945]

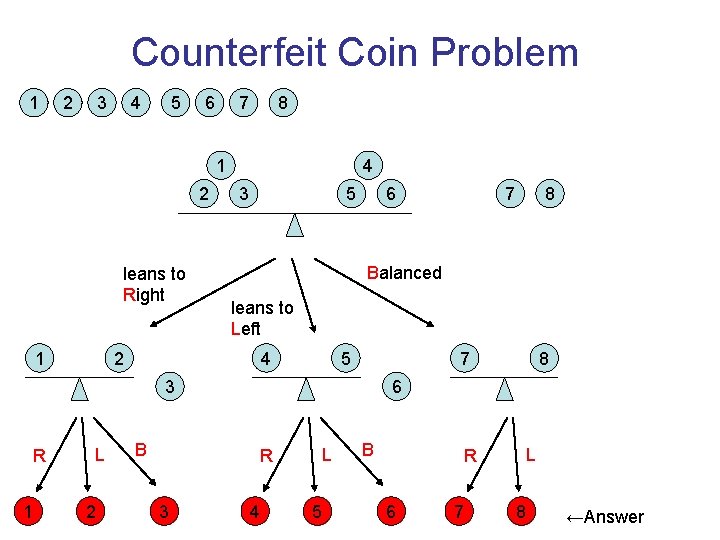
Counterfeit Coin Problem 1 2 3 4 5 6 7 8 1 2 leans to Right 1 4 3 5 6 leans to Left 2 1 L 4 2 B 5 7 8 6 R 3 8 Balanced 3 R 7 4 L 5 B R 6 7 L 8 ←Answer

Counterfeit Coin Problem There have been several different versions and extensions in the literature, say, • more counterfeit coins, • whether the counterfeit coins are underweight or overweight, • they have the equal weight or not, and so on. Here, we assume: • k false coins with equal weight are included in N given coins. • The balance scale gives us only binary information, balanced (i. e. , two sets of coins on the pans are equal in weight) or titled (different in weight) The goal is to find all the k false coins.

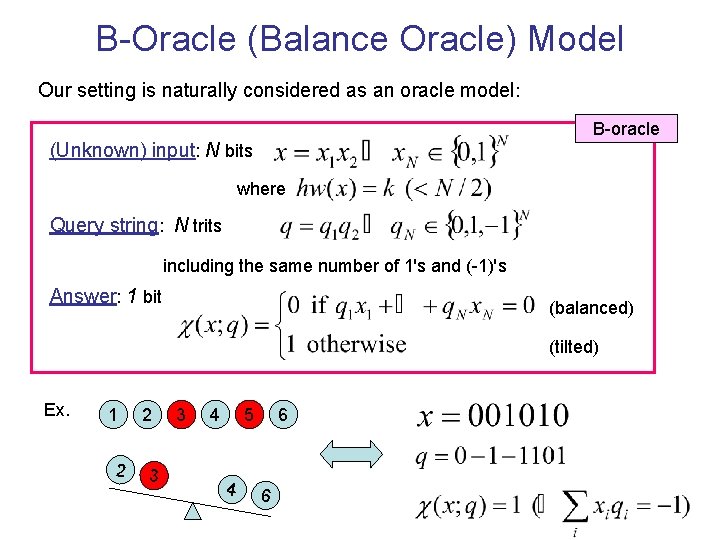
B-Oracle (Balance Oracle) Model Our setting is naturally considered as an oracle model: B-oracle (Unknown) input: N bits where Query string: N trits including the same number of 1's and (-1)'s Answer: 1 bit (balanced) (tilted) Ex. 1 2 2 3 3 4 5 4 6 6

B-Oracle (Balance Oracle) Model Our setting is naturally considered as an oracle model: B-oracle (Unknown) input: N bits where Query string: N trits including the same number of 1's and (-1)'s Answer: 1 bit (balanced) (tilted) When k=1, the query complexity (of finding the false coin) is log 2 N, which is also an information theoretic lower bound.

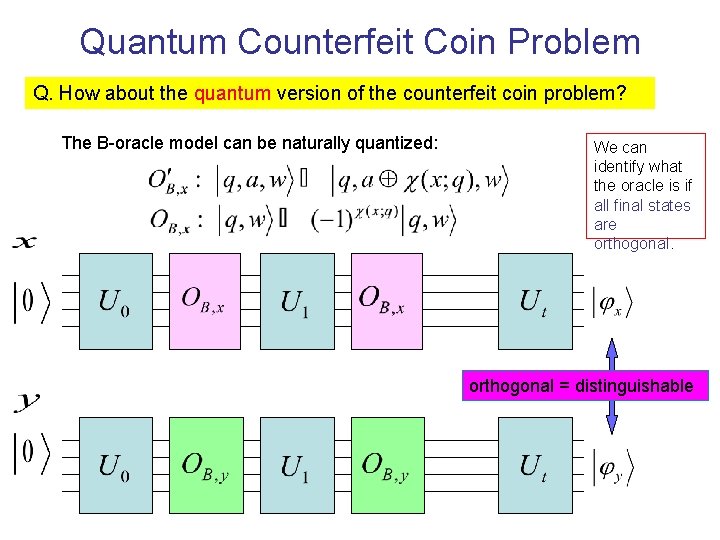
Quantum Counterfeit Coin Problem Q. How about the quantum version of the counterfeit coin problem? The B-oracle model can be naturally quantized: We can identify what the oracle is if all final states are orthogonal = distinguishable

Quantum Counterfeit Coin Problem Our goal is to answer the following question: Q. What is the quantum query complexity of finding all the k false coins, that is, identifying the input x? Results k=1 k=2 k=3 general Quantum 1 1 2≤ k ≤ 3 O(k 1/4) Classical log N ≥ 2 log(N/2) ≥ 3 log(N/3) Ω(k log(N/k)) quartic speed-up (Note) So far, there are few natural problems whose quantum speed-up are between quadratic and exponential (ex. cubic [van Dam-Shparlinski 08]).

Algorithm

B-Oracle and IP oracle Notice a similarity between the B-oracle and the IP (Inner Product) oracle! (Unknown) input: N bits B-oracle where Query string: N trits including the same number of 1's and (-1)'s Answer: 1 bit (balanced) (tilted) (Unknown) input: N bits Query string: N bits Answer: 1 bit IP oracle

Case: k=1 [cf. Terhal-Smolin 1998] When k=1 (and the Hamming weight of the query string is even), the B-oracle can simulate IP oracle! Key Fact So, we can identify the oracle by only 1 query! Bernstein-Vazirani 1997 query to B-oracle The first half of the nonzero entries are 1 and the last half are 1 under a reversible operation orthogonal = distinguishable

General k In general, B-oracle and IP oracle are much different. But, we can still simulate IP oracle by O(k 1/4) queries to B-oracle! Algorithm: Find*(k) Find balanced pairs by the Grover search (exactly, amplitude amplification) If the Grover search finds a solution (=balanced pair), do nothing. Otherwise flip the phase. basis change

Lower bounds

Lower Bounds under Restricted Pan-size L: =the size of the pans (=the number of coins placed on each pan) L ≥ l (L ≤ l, resp. ) denotes the restriction that we should place at least l (at most l, resp. ) coins the pans whenever we use the balance. [Lower bound under Restricted Pan-size] If L ≤ N/k 1+2εor L ≥ N/k 1 -4ε, then Ω(kε) queries are needed. In particular, if L ≤ O(N/k 1. 5) or L ≥ Ω(N), then tight lower bound Ω(k 1/4) can be obtained. or (Note) Algorithm Find*(k) is easily modified so that L ≥ Ω(N) can be satisfied.

For Quantum Lower Bounds Two standard techniques • Polynomial methods [Beals-Buhrman-Cleve-Mosca-de Wolf 1998] • Adversary methods [Ambainis 2000] =1 orthogonal = distinguishable

Lower Bounds under Restricted Pan-size L: =the size of the pans (=the number of coins placed on each pan) L ≥ l (L ≤ l, resp. ) denotes the restriction that we should place at least l (at most l, resp. ) coins the pans whenever we use the balance. [Lower bound under Restricted Pan-size] placing many coins gives little information If L ≤ N/k 1+2εor L ≥ N/k 1 -4ε, then Ω(kε) queries are needed. In particular, if L ≤ O(N/k 1. 5) or L ≥ Ω(N), then tight lower bound Ω(k 1/4) can be obtained. placing few coins gives little information k 1/5 l N/k 1/5 (Note) Algorithm Find*(k) is easily modified so that L ≥ Ω(N) can be satisfied.

More Witness on the tightness of the O(k 1/4)-Algorithm Notice that our algorithm is always used in such a way that the partition of the coins into the two pans is done uniformly at random. There seems no essentially better ways than this when using the B-oracle. . . [Lower bound under "random-partition assumption" ] (Informal Statement) If the use of B-oracle is restricted so that the set of coins placed on the two pans can be partitioned into the left pan and right pan uniformly at random, we need Ω(k 1/4) queries. To show this statement rigorously, • need to extend an oracle operation in a ''stochastic'' form • extend an adversary method to the "stochastic'' oracle

Conclusion • We have investigated the quantum query complexity of finding k false coins from N coins by using the B-oracle, which represents a balance scale. • We have obtained upper bound O(k 1/4), contrasting with the classical lower bound Ω(klog(N/k)). So this achieves quartic speed-up for a natural problem. • We do not have a matching lower bound, but we have obtained several tight lower bounds under different restrictions of the ways that algorithms can take. At least, they imply that we need a radically new algorithm to beat the current upper bound.