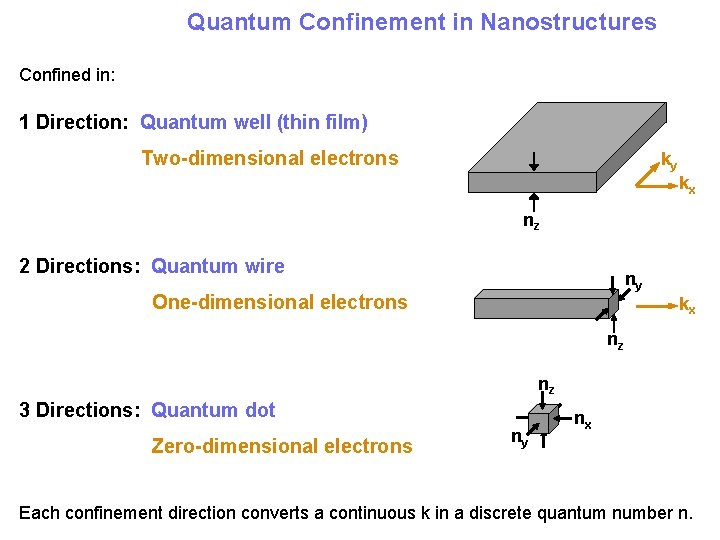
Quantum Confinement in Nanostructures Confined in 1 Direction

Quantum Confinement in Nanostructures Confined in: 1 Direction: Quantum well (thin film) Two-dimensional electrons ky kx nz 2 Directions: Quantum wire ny One-dimensional electrons kx nz nz 3 Directions: Quantum dot Zero-dimensional electrons ny nx Each confinement direction converts a continuous k in a discrete quantum number n.

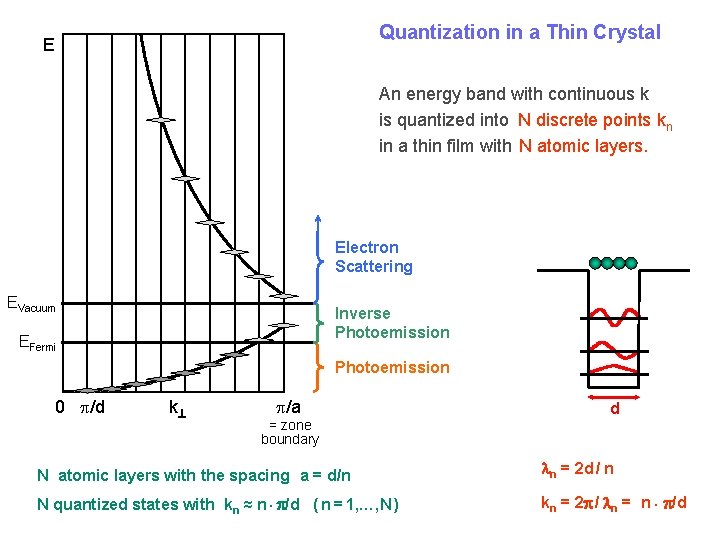
Quantization in a Thin Crystal E An energy band with continuous k is quantized into N discrete points kn in a thin film with N atomic layers. Electron Scattering EVacuum Inverse Photoemission EFermi Photoemission 0 /d k /a = zone boundary d N atomic layers with the spacing a = d/n n = 2 d / n N quantized states with kn ≈ n /d ( n = 1, …, N ) kn = 2 / n = n /d

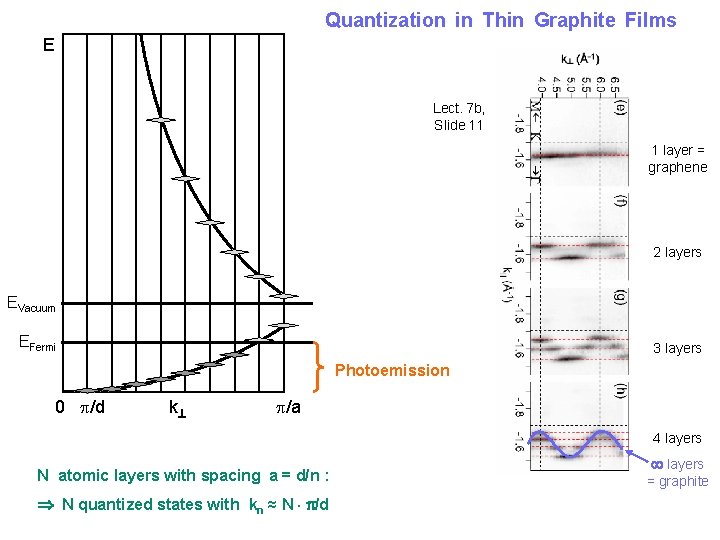
Quantization in Thin Graphite Films E Lect. 7 b, Slide 11 1 layer = graphene 2 layers EVacuum EFermi 3 layers Photoemission 0 /d k /a 4 layers N atomic layers with spacing a = d/n : N quantized states with kn ≈ N /d layers = graphite

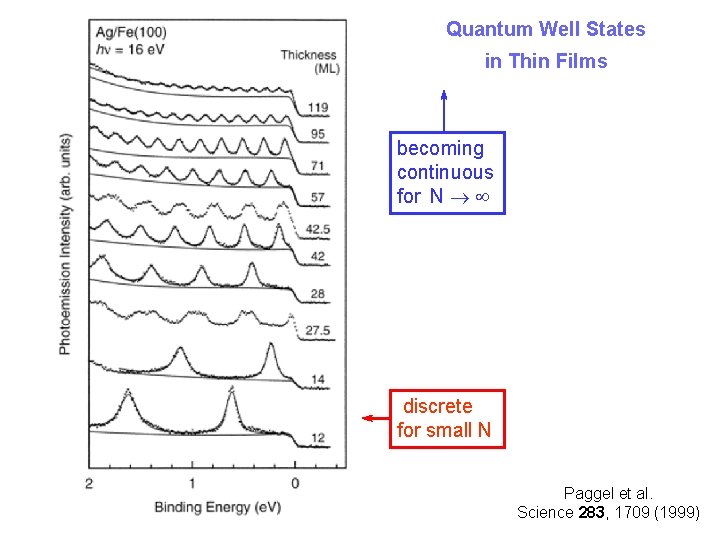
Quantum Well States in Thin Films becoming continuous for N discrete for small N Paggel et al. Science 283, 1709 (1999)

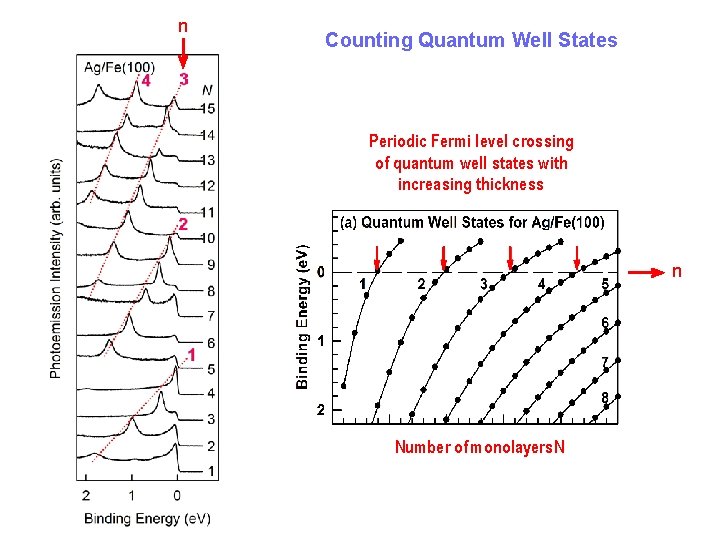
n Counting Quantum Well States Periodic Fermi level crossing of quantum well states with increasing thickness n Number of monolayers N

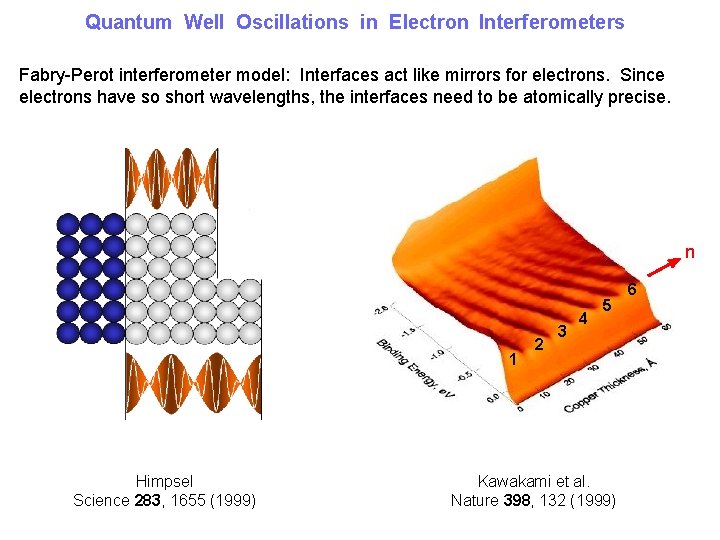
Quantum Well Oscillations in Electron Interferometers Fabry-Perot interferometer model: Interfaces act like mirrors for electrons. Since electrons have so short wavelengths, the interfaces need to be atomically precise. n 1 Himpsel Science 283, 1655 (1999) 2 3 4 5 Kawakami et al. Nature 398, 132 (1999) 6

The Important Electrons in a Metal Energy EFermi Energy Spread 3. 5 k. BT Transport (conductivity, magnetoresistance, screening length, . . . ) Width of the Fermi function: FWHM 3. 5 k. BT Phase transitions (superconductivity, magnetism, . . . ) Superconducting gap: Eg 3. 5 k. BTc (Tc= critical temperature)

Energy Bands of Ferromagnets Ni Photoemission data Energy Relative to EF [e. V] Calculation 0. 7 0. 9 k|| along [011] 1. 1 [Å-1 ] States near the Fermi level cause the energy splitting between majority and minority spin bands in a ferromagnet (red and green).

Quantum Well States and Magnetic Coupling The magnetic coupling between layers plays a key role in giant magnetoresistance (GMR), the Nobel prize winning technology used for reading heads of hard disks. This coupling oscillates in sync with the density of states at the Fermi level. (Qiu, et al. PR B ‘ 92)

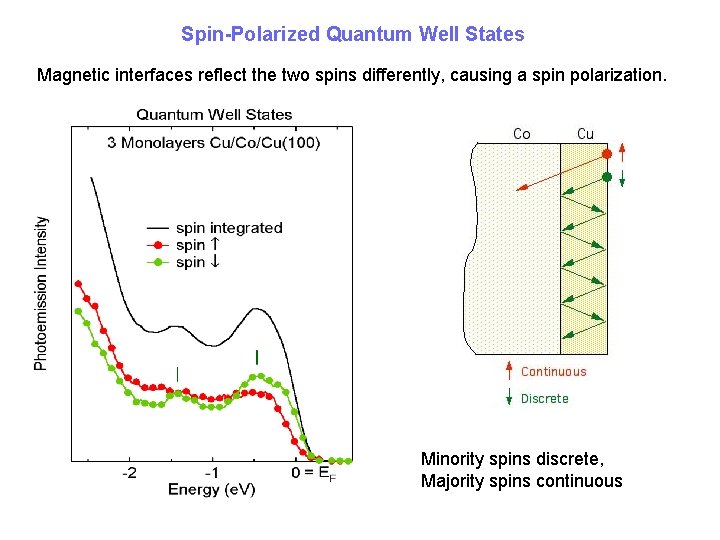
Spin-Polarized Quantum Well States Magnetic interfaces reflect the two spins differently, causing a spin polarization. Minority spins discrete, Majority spins continuous

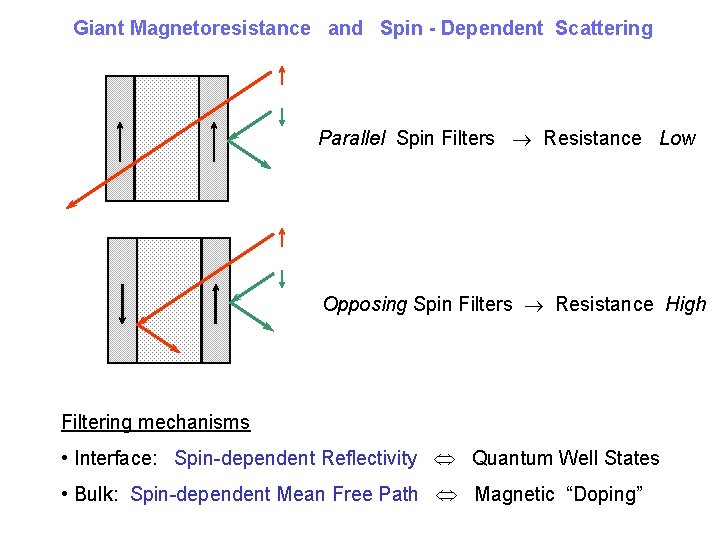
Giant Magnetoresistance and Spin - Dependent Scattering Parallel Spin Filters Resistance Low Opposing Spin Filters Resistance High Filtering mechanisms • Interface: Spin-dependent Reflectivity Quantum Well States • Bulk: Spin-dependent Mean Free Path Magnetic “Doping”

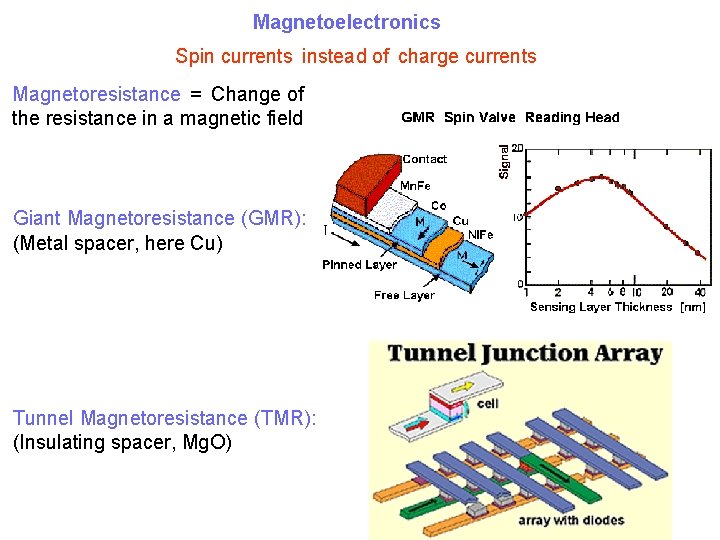
Magnetoelectronics Spin currents instead of charge currents Magnetoresistance = Change of the resistance in a magnetic field Giant Magnetoresistance (GMR): (Metal spacer, here Cu) Tunnel Magnetoresistance (TMR): (Insulating spacer, Mg. O)