Quantum computing with classical bits 9 Measurements conditional

Quantum computing with classical bits

(9) Measurements, conditional probabilities and the “paradoxes” of quantum mechanics

Quantum mechanics can arise from classical statistics !

Quantum formalism for classical statistics can be useful for understanding how information propagates in probabilistic systems

Correlations , conditional probabilities and Bell’s inequalities

(a) conditional probabilities and reduction of wave function

Probability distribution w(t) w(tin) = Todays w(t 0)not very suitable for statement , if here and now a pointer falls down :

one probability distribution or wave function of the Universe not useful for the computation of conditional probabilities reset initial conditions after each measurement same setting in all probabilistic theories, classical or quantum

Schrödinger’s cat conditional probability : if nucleus decays then cat dead with wc = 1 (reduction of wave function)

decoherence no superposition state of dead and living cat can be realized not discussed here

reduction of wave function nucleus decays with a certain decay probability: quantum state is superposition of eigenstate 1 : nucleus intact and eigenstate 2 : decay products If decay is measured: Reduction of wave function to eigenstate 2

conditional probability two observables A and B n both with possible values +1 or -1 n A : cat alive (1) or dead (-1) n B : nucleus decays (1) or not (-1) n

conditional probabilities and measurements n conditional probabilities depend on the way how measurements are done n not uniquely given by probability distribution need of additional input n concept of ideal measurements n

conditional probability to find A=1 after measurement of B=1 Ideal measurements : eliminate after first measurement B=1 all possibilities that B=-1 and set new “initial condition” This is the general

conditional probabilities and correlation function probabilitiy to find A=�� , B=�� not necessarily the simultaneous probability that A and B have these values in a given state

Ideal measurements ideal classical measurement : n use classical correlation function ideal measurement in quantum subsystem: n result should only depend on information available for the subsystem. n typically, classical correlation function cannot be used !

conditional probability and reduction of wave function Expectation value of A after measurement of B=1 can be computed by replacing after the measurement B=1 the original wave function by an eigenstate to B with eigenvalue B=1. Reduction of wave function Eliminate from the wave function all components that have not been measured ( e. g. B=-1) and normalize again. Unique only for one- qubit system !

conditional probabilities for ideal measurement in one-qubit subsystem probability to find A=1 after measurement of B=1 conditional probabilities can be expressed in terms of expectation value of A in eigenstate of B

reduction of wave function n n convenient method to compute conditional probabilities same in classical statistics : after first measurement of B : eliminate from probability distribution all parts corresponding to values of B that have not been measured, and normalize again same for classical wave function elimination often not unique ! exceptions are twolevel systems QM : reduction of wave function is unique only for

reduction of wave function is a technical way to describe conditional probabilities n not a unitary evolution of the quantum state n

reduction of wave function not needed for computation of conditional probabilities QM : compute conditional probabilities from quantum correlation function ( two state system or complete set of measurements ) n Assumes that ideal quantum measurement does not disturb the unitary evolution of the quantum system n

conditional probabilities from unitary evolution of quantum subsystem : quantum correlation function probabilitiy to find A=�� , B=�� All expectation values can be computed from evolution of the wave function without reduction of the wave function

conditional probabilities from correlation function same result from unitary evolution

conditional probability and unitary evolution conditional probabilities can be computed from standard unitary evolution of wave function by evaluating appropriate correlation functions n reduction of wave function not needed, but very useful for a simple description n

(b) conditional correlations

Sequences of measurements are defined by conditional correlations

conditional correlation from conditional probabilities n Invert the relations of the type in order to define the conditional correlation n The conditional correlation for one qubit system equals the quantum correlation defined by the product of operators

(c) EPR - paradoxon

Reality n Correlations are physical reality , not only expectation values or measurement values of single observables n Correlations can be non-local ( also in classical statistics ) ; Causal processes needed only for establishment of non-local correlations at some earlier stage. Correlated systems cannot be separated into independent parts – The whole is more than

EPR - paradoxon Spin 0 decay : correlation between the two spins of the decay products is established at decay No contradiction to causality, locality or reality, if correlations are understood as part of reality ( for once not right… )

EPR - paradoxon Recall : reduction of wave function is not a physical process ! Conditional probability for spin B up , spin A down equals one , because of correlation

)d( Bell’s inequalities

Bell’s inequalities for classical correlation functions Classical observables Classical correlation function obeys Bell’s inequalities Measurements in quantum systems show violation of Bell’s inequalities

Bells inequalities Identities for classical correlation functions correlation map : need to be obeyed by selected quantum correlations

CHSH inequalities generalize Bell inequalities choose :

How correlations in classical statistical systems can violate Bell’s inequalities (i) not all observables may be classical observables for A , B both classical observables : correlation function relevant for measurements may not be given by classical correlation function (ii)

(ii) measurement correlations are not classical correlations n example 1 : conditional correlations n example 2 : function observables

(1) conditional/quantum correlation conditional correlation compatible with quantum subsystems in classical statistics equals quantum correlation ! n using conditional correlations in classical statistics : no contradiction to Bell’s inequalities n

quantum correlations and coarse graining n n n quantum features in classical statistical systems are typically related to coarse graining wave functions or density matrix contain only subsystem information – much less information than overall probability distribution coarse graining of information incomplete statistics classical correlation function may exist, but not be compatible with coarse graining

quantum correlations and coarse graining n n n many classical observables mapped to same local observables equivalence class of classical observables : all observables that correspond to same local observable local system and environment : equivalence class is system property measurement correlation should not depend on environment, only on equivalence classes classical correlation depends on environment , conditional correlation not

(2) function observables and coarse graining of microphysical classical statistical ensemble particle concept not unique one more example for non – commutativity in classical statistics

microphysical ensemble n states τ n labeled by sequences of occupation numbers or bits ns = 0 or 1 n τ = [ ns ] = [0, 0, 1, 1, 1, 1, 0, …] etc. n probabilities pτ > 0

classical correlation Classical local observables are functions of local occupation numbers n Their classical correlations can be computed from local probabilities n Classical correlations obey Bell’s inequalities n

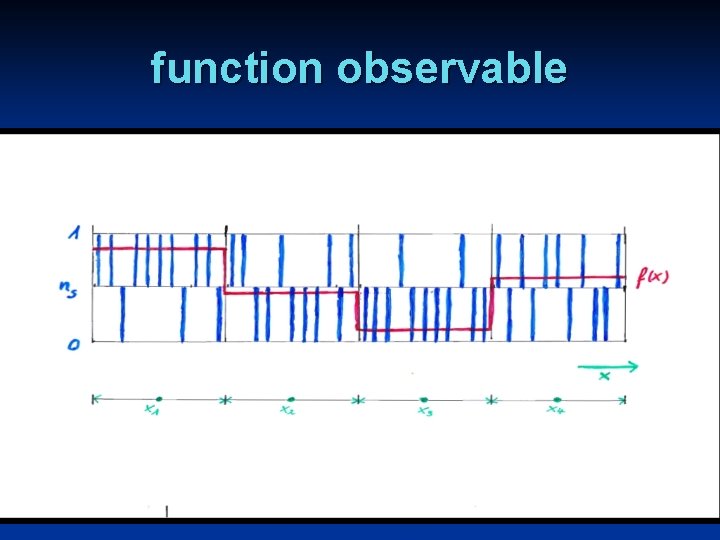
function observable

function observable normalized difference between occupied and empty bits in interval I(x 1) I(x 2) I(x 3) I(x 4)

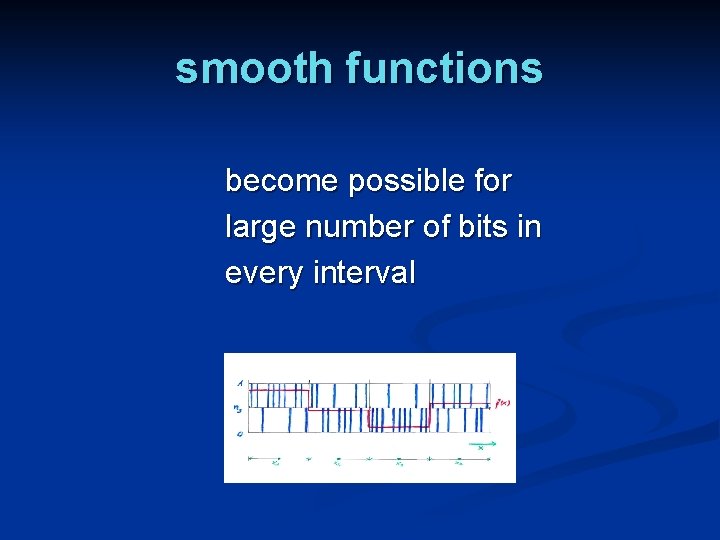
smooth functions become possible for large number of bits in every interval

generalized function observable normalization classical expectation value several species α

position classical observable : fixed value for every state τ

momentum n derivative observable classical observable : fixed value for every state τ

complex structure

classical product of position and momentum observables commutes ! and obeys Bell’s inequalities

different products of observables differs from classical product

Which product describes correlations of measurements ?

coarse graining of information for subsystems

density matrix from coarse graining • position and momentum observables use only small part of the information contained in pτ , • relevant part can be described by density matrix • subsystem described only by information which is contained in density matrix • coarse graining of information

quantum density matrix has the properties of a quantum density matrix

quantum operators

quantum product of observables the product is compatible with the coarse graining and can be represented by operator pro

incomplete statistics classical product n n is not computable from information which is available for subsystem ! cannot be used for measurements in the subsystem !

classical and quantum dispersion

subsystem probabilities in contrast :

squared momentum quantum product between classical observable maps to product of quantum operators

non – commutativity in classical statistics commutator depends on choice of product

observables and coarse graining In the coarse grained system P is no longer a classical observable n P contains derivatives acting on the wave function n

measurement correlation between measurements of positon and momentum is given by quantum product n this correlation is compatible with information contained in subsystem n

coarse graining from fundamental fermions at the Planck scale to atoms at the Bohr scale p([ns]) ρ(x , x´)

classical correlation pointwise multiplication of classical observables n not available on level of subsystem observables n definition depends on details of classical observables , while many different classical observables correspond to the same observable in quantum subsystem n classical correlation depends on probability distribution for the quantum subsystem and its needed : correlation that can be environment n computed in terms of local observables and wave functions or density matrix !

classical or conditional correlation ? Classical correlation appropriate if two measurements do not influence each other and if simultaneous probabilities for values of both observables are available. n Conditional correlation takes into account conditions after first measurement. Two measurements of same subsystem observable immediately after each other should yield the same value ! n

quantum correlation given by operator product of quantum operators n appropriate if ideal measurement does not disturb the unitary evolution of the subsystem n equals conditional correlation in this case n can be computed from information in the subsystem n

Can quantum physics be described by classical probabilities ? “ No go “ theorems Bell , Clauser , Horne , Shimony , Holt implicit assumption : use of classical observables and classical correlation function for correlation between measurements Kochen , Specker assumption : unique map from operators to classical observables

conclusion n quantum statistics emerges from classical statistics wave function, superposition, interference, entanglement unitary time evolution of quantum mechanics can be described by suitable time evolution of classical probabilities conditional correlations for measurements both in quantum and classical statistics

quantum mechanics from classical statistics probability amplitude n entanglement n interference n superposition of states n fermions and bosons n unitary time evolution n transition amplitude n non-commuting operators n

what is an atom ? quantum mechanics : isolated object n quantum field theory : excitation of complicated vacuum n classical statistics : sub-system of ensemble with infinitely many degrees of freedom n

Quantum particle n n n Quantum field theory for Dirac fermions in external electromagnetic field can be described by suitable time evolution equation for classical local probabilities Includes discrete time steps and complex structure One particle state, non-relativistic limit yields Schroedinger equation for particle in potential Entangled two fermion states open : overall classical statistical probability distribution that accounts for such an evolution

end

(2) conditional correlation A, B : two-level observables = ( ) sum over coarse grained states �� simultaneous probabilities for values of both observables are not available for states ��

conditional correlation probability to find value +1 for product of measurements of A and B probability to find A=1 after measurement of B=1 … can be expressed in terms of expectation value of A in eigenstate of B

conditional product n conditional product of observables n conditional correlation n does it commute ?

conditional correlation and anticommutators n conditional two point correlation commutes =

conditional three point correlation

conditional three point correlation in quantum language n conditional three point correlation is not commuting !

conditional correlations and operators n conditional correlations in classical statistics can be expressed in terms of operator products

non – commutativity of operator product is closely related to properties of conditional correlations !