Quantum computing with classical bits 6 Quantum operations

Quantum computing with classical bits

(6) Quantum operations with artificial neural networks

Artificial neural networks n Can neural networks learn to perform quantum operations ?

Quantum computing quantum computing proceeds by quantum gates n discrete unitary transformations of density matrix in consecutive time steps n n a few basic gates are sufficient

Probabilistic computing The outcome of a computation step is not a fixed classical state ( e. g. fixed bit configuration ) n It results in a probability distribution for the available classical states n Either initial state is probabilistic, or operation is probabilistic n Stepwise manipulation of probability distributions n

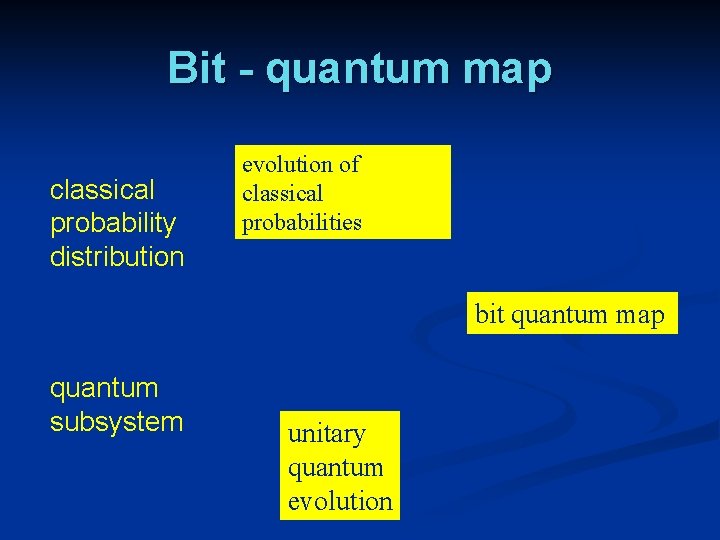
Bit - quantum map classical probability distribution evolution of classical probabilities bit quantum map quantum subsystem unitary quantum evolution

Complete bit – quantum map n every positive density matrix of the quantum subsystem can be realized by suitable classical probability distribution n then all quantum operations can be performed by suitable changes of classical probability distribution

Two qubits SU(4)- generators : use fifteen classical bits or use eight classical bits and correlations different bit - quantum maps

Quantum gates Unitary transformation of density matrix Single qubit: Rotation Hadamard gate Two qubits: CNOT gate

CNOT gate for two qubits SU(4)generators : CNOT – gate: to be achieved by suitable change of probability distribution for fifteen classical bits : deterministic

Entanglement n CNOT - gate transforms product state for two qubits into entangled state n All unitary operations for two qubits can be constructed from Hadamard, rotation and CNOT gates.

Artificial neural networks n Can neural networks learn to perform quantum operations ?

Three layer network Task : learn unitary quantum operations for two- qubit quantum system n Input layer : 64 real neurons n Bottleneck layer : m real neurons n Output layer : 64 real neurons n

Optimization Maps between layers involve parameters that can be adapted during the learning n Neural network learns how to adapt the map between layers such that the result on the output layer is optimal n Goal is defined n Supervised learning : network learns with examples n

Learning unitary operations step 1: quantumness gate learns to map input information on two – qubit density matrix step 2 : learns basic quantum gates for unitary operations individually

Matrices 64 real numbers of input and output layers are sufficient to store the elements of a real 8 x 8 matrix Complex 4 x 4 matrices can be represented as real 8 x 8 matrices with particular complex structure

Complex matrices Combine and into complex matrix Multiplication of real matrices with structure is compatible with complex matrix multiplication

Learn complex positive matrix n Transform arbitrary real 8 x 8 input matrix to complex positive 4 x 4 matrix positive hermitean 4 x 4 matrix; has representation as

Learning unitary operations step 1: quantumness gate learns to map input information on two – qubit density matrix step 2 : learns basic quantum gates for unitary operations individually

Learning a quantum gate n For given input density matrix, and given unitary operation to be learned , the output density matrix is uniquely specified n Learn by minimizing the difference to the output matrix by using a random training set of input matrices

Learning unitary operations loss : difference to “ correct” output matrix

Bottleneck Critical bottleneck dimension corresponds to number of independent elements of twoqubit density matrix m m

Learn basic quantum gates Unitary transformation of density matrix Single qubit: Rotation Hadamard gate Two qubits: CNOT gate

Learning unitary operations learns : normalization hermiticity of output matrix

Chain of unitary transformations After the learning phase the network can perform arbitrary chains of unitary transformations

Dense covering of generalized Bloch sphere

Probabilistic computing n So far only map of expectation values n Probabilistic computing : map probability distributions that produce these expectation values

Conclusion Quantum operations can be performed by classical statistical systems n Very low temperature or well isolated systems of microscopic qubits not needed ! n

end