Quantum Computing Whats It Good For Scott Aaronson

Quantum Computing: What’s It Good For? Scott Aaronson Computer Science Department, UC Berkeley January 10, 2002 www. cs. berkeley. edu/~aaronson

Overview 1. History and background 2. The quantum computation model 3. Example: Simon’s algorithm 4. Other algorithms (Shor’s, Grover’s) 5. Limits of quantum computing, including recent work 6. The future

Richard Feynman (1981): “. . . trying to find a computer simulation of physics, seems to me to be an excellent program to follow out. . . and I'm not happy with all the analyses that go with just the classical theory, because nature isn’t classical, dammit, and if you want to make a simulation of nature, you'd better make it quantum mechanical, and by golly it's a wonderful problem because it doesn't look so easy. ”

David Deutsch (1985): “Computing machines resembling the universal quantum computer could, in principle, be built and would have many remarkable properties not reproducible by any Turing machine … Complexity theory for [such machines] deserves further investigation. ”

What Is Quantum Mechanics?

What Is Quantum Mechanics? Traditional Physics View Quantum Computing View Framework for atomic-scale Computational model with physical theories amplitudes instead of probabilities Complicated (lots of integral Simple signs) Pessimistic (i. e. Heisenberg Optimistic (i. e. Shor’s uncertainty relation) factoring algorithm)

The Model • Computer has n bits of memory • Classical case: if n=2, possible states are 00, 01, 10, 11 • Randomized case: States are vectors of 2 n probabilities in [0, 1] i. e. Pr[00]=0. 2 Pr[01]=0. 2 Pr[10]=0. 1 Pr[11]=0. 5 • Quantum case: States are vectors of 2 n complex numbers called amplitudes

The Model (con’t) • Dirac ket notation: We write state as, i. e. , 0. 5 |00 - 0. 5 |01 + 0. 5 i |10 - 0. 5 i |11 Superposition over basis states • Normalization: If state is i i|i , then i| i|2 = 1 (Why complex numbers? Why | i|2 and not i 2? )

Measurement • When we measure state, see basis state |i with probability | i|2 • Furthermore, state collapses to |i • Can also make partial measurements • Example: Measuring 1 st bit of yields |00 with ½ prob. , (|10 +|11 )/ 2 with ½ prob.

Time Evolution • Matrix U is unitary iff UU†=I, † conjugate transpose Equivalently: U preserves norm • Can multiply amplitude vector by some unitary U (i. e. replace state | by U| ) • Quantum analogue of Markov transitions

Example: Square Root of NOT • Hadamard matrix: H|0 = (|0 +|1 )/ 2 H|1 = (|0 -|1 )/ 2 H(|0 +|1 )/ 2 = |0 H(|0 -|1 )/ 2 = |1

Quantum Circuits • Unitary operation is local if it applies to only a constant number of bits (qubits) • Given a yes/no problem of size n: 1. Apply order nk local unitaries for constant k 2. Measure first bit, return ‘yes’ iff it’s 1 • BQP: class of problems solvable by such a circuit with error probability at most 1/3 (+ technical requirement: uniformity)

The Power of Quantum Computing • Bernstein-Vazirani 1993: BPP BQP PSPACE BPP: solvable classically with order nk time PSPACE: solvable with order nk memory • Apparent power of quantum computing comes from interference - Probabilities always nonnegative - But amplitudes can be negative (or complex), so paths leading to wrong answers cancel each other out

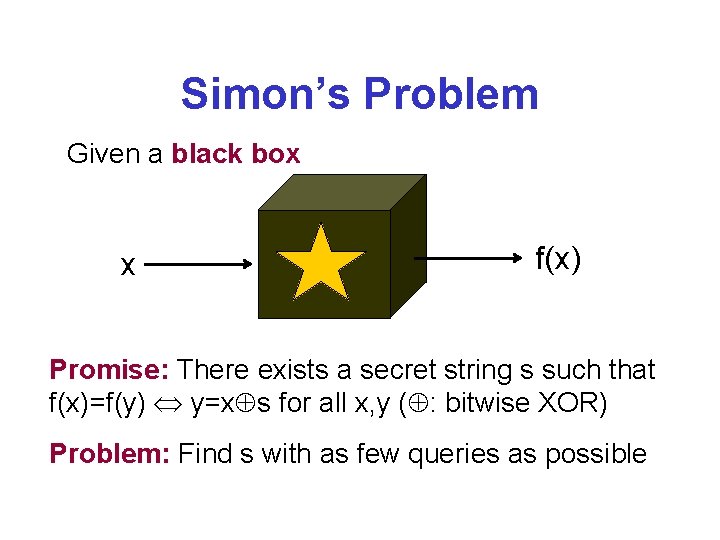
Simon’s Problem Given a black box x f(x) Promise: There exists a secret string s such that f(x)=f(y) y=x s for all x, y ( : bitwise XOR) Problem: Find s with as few queries as possible

Example Input x 000 001 010 011 100 101 110 111 Output f(x) 4 2 3 1 2 4 1 3 Secret string s: 101 f(x)=f(x s)

Simon’s Algorithm • Classically, order 2 n/2 queries needed to find s - Even with randomness • Simon (1993) gave quantum algorithm using only order n queries • Assumption: given |x , can compute |x |f(x) efficiently

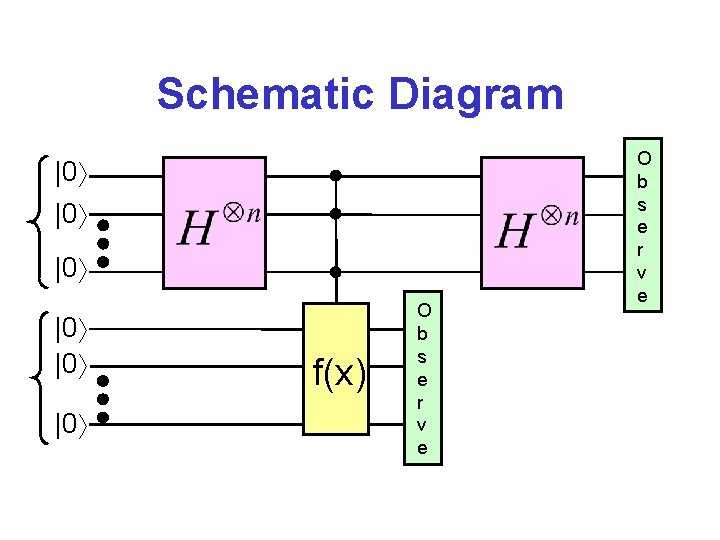
Simon’s Algorithm (con’t) 1. Prepare uniform superposition 2. Compute f: 3. Measure |f(x) , yielding for some x

Simon’s Algorithm (con’t) 4. Apply to each bit of Result: where

Simon’s Algorithm (con’t) 5. Measure. Obtain a random y such that 6. Repeat steps 1 -5 order n times. Obtain a linear system over GF 2: 7. Solve for s. Can show solution is unique with high probability.

Schematic Diagram |0 |0 |0 f(x) O b s e r v e

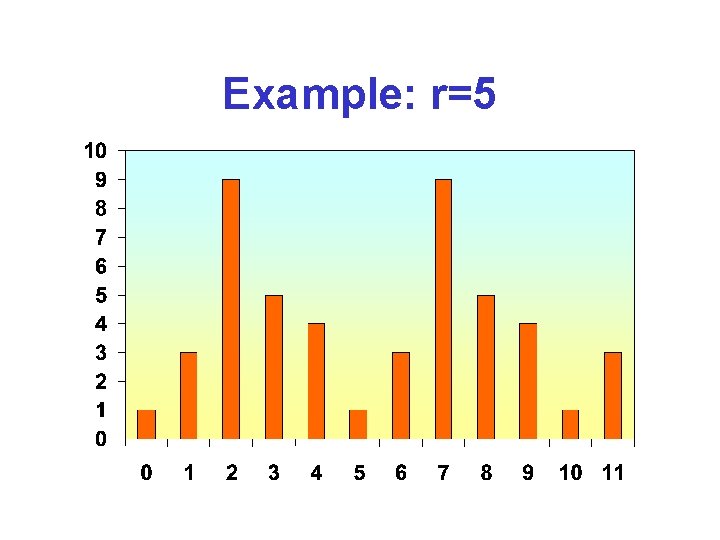
Period Finding • Given: Function f from {1… 2 n} to {1… 2 n} Promise: There exists a secret integer r such that f(x)=f(y) r | x-y for all x Problem: Find r with as few queries as possible • Classically, order 2 n/3 queries to f needed • Inspired by Simon, Shor (1994) gave quantum algorithm using order poly(n) queries

Example: r=5

Factoring and Discrete Log • Using period-finding, can factor integers in polynomial time (Miller 1976) • Also discrete log: given a, b, N, find r such that ar b(mod N) • Breaks widely-used public-key cryptosystems: RSA, Diffie-Hellman, El. Gamal, elliptic curve systems…

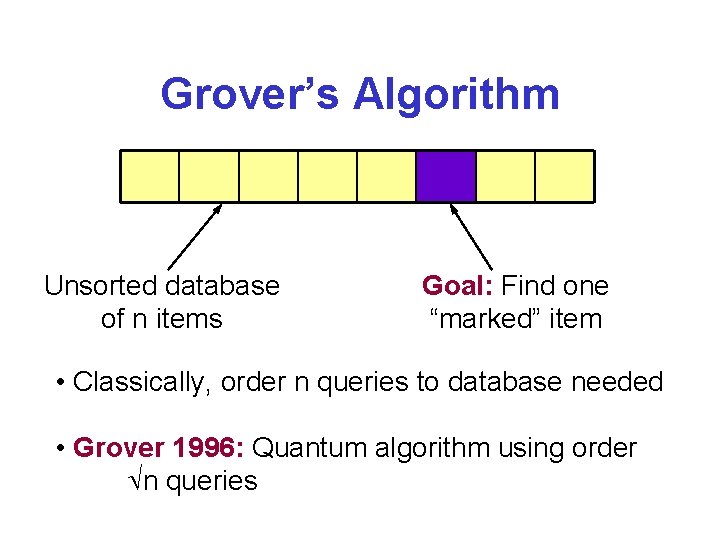
Grover’s Algorithm Unsorted database of n items Goal: Find one “marked” item • Classically, order n queries to database needed • Grover 1996: Quantum algorithm using order n queries

Limits of Quantum Computing • Bennett et al. 1996: Grover’s algorithm is optimal (Quantum search requires order n queries) • Beals et al. 1998: For all total Boolean functions f: {0, 1}n {0, 1}, if quantum algorithm to evaluate f uses T queries, exists classical algorithm using order T 6 queries.

Collision Problem • Given: a function f: {1, …, n} {1, …, N}, n even Promise: f is either 1 -1 (i. e. 3, 7, 9, 2) or 2 -1 (5, 2, 2, 5) Problem: Decide which • Models graph isomorphism, breaking cryptographic hash functions • Classical algorithm needs order n queries to f • Brassard et al. 1997: Quantum algorithm using n 1/3 queries

Collision Lower Bound • Can a quantum algorithm do better than n 1/3? Previously couldn’t even rule out constant number of queries! • A 2001: Any quantum algorithm for collision needs order n 1/5 queries • Shi 2001: Improved to order n 1/3

The Future

The Future • When processor components reach atomic scale, Moore’s Law breaks down - Quantum effects become important whether we want them or not - But huge obstacles to building a practical quantum computer!

Implementation

Implementation • Key technical challenge: prevent decoherence, or unwanted interaction with environment • Approaches: NMR, ion trap, quantum dot, Josephson junction, optical… • Recent achievement: 15=3 5 (Chuang et al. 2001) • Larger computations will require quantum errorcorrecting codes

Quantum Computing: What’s It Good For? • Potential (benign) applications - Faster combinatorial search - Simulating quantum systems • ‘Spinoff’ in quantum optics, chemistry, etc. • Makes QM accessible to non-physicists • Surprising connections between physics and CS • New insight into mysteries of the quantum