Quantum Computing Preethika Kumar Classical Computing MOSFET CMOS

Quantum Computing Preethika Kumar

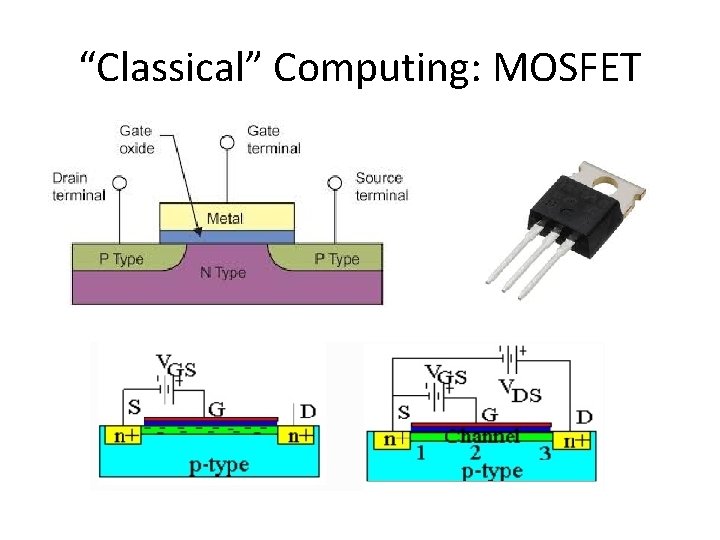
“Classical” Computing: MOSFET

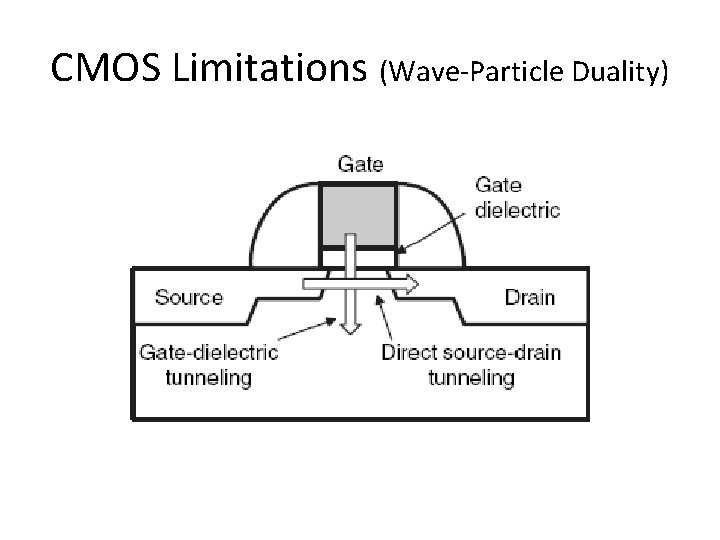
CMOS Limitations (Wave-Particle Duality)

In the Quantum World…. . • Bits become qubits: “ 0”, “ 1” or “both” Probability of measuring|0 Probability of measuring|1 Junction I I • Unitary matrices become quantum gates: We have a universal set of gates

Schrödinger Equation Newton’s Law of the Little World Hamiltonian: 2 n non-diagonal matrix

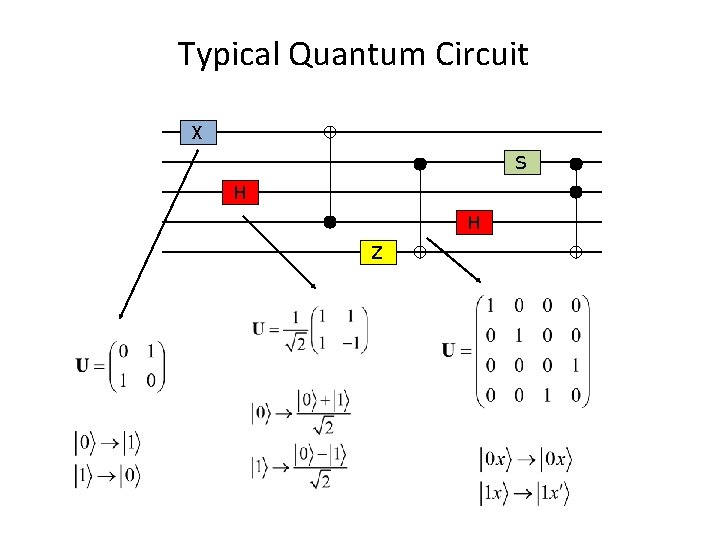
Typical Quantum Circuit X S H H Z

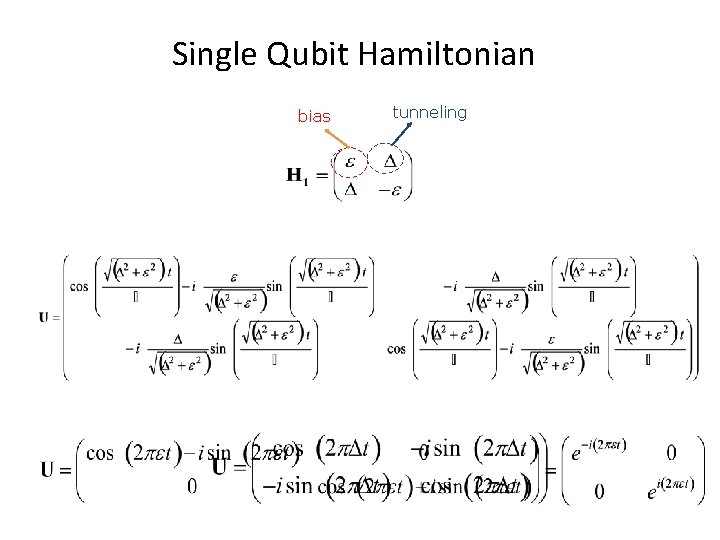
Single Qubit Hamiltonian bias tunneling

Single Qubit Hamiltonian bias tunneling

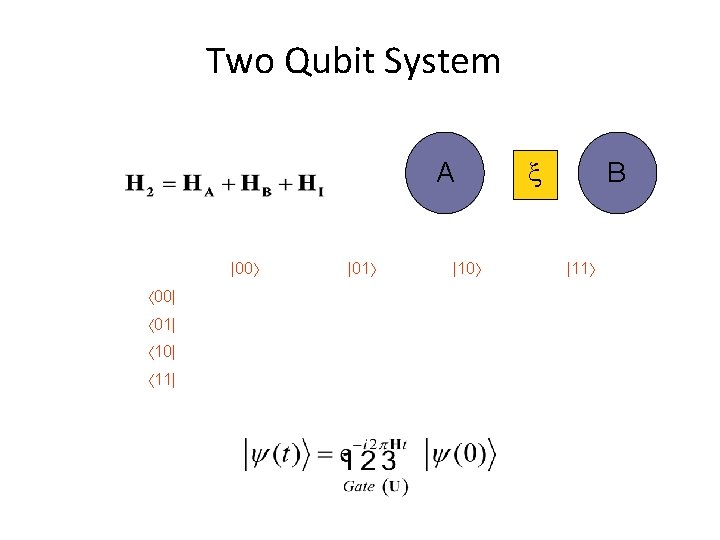
Two Qubit System A |00 00| 01| 10| 11| |01 |10 B |11

Some Potential Challenges • No Cloning Theorem - moving quantum data (fan-out) - quantum error correction (redundancy) • Measurements collapse quantum states - closed quantum systems (coupling with environment) - quantum error correction (syndromes) • Architectural layouts: limited interactions - gate operations - moving quantum data

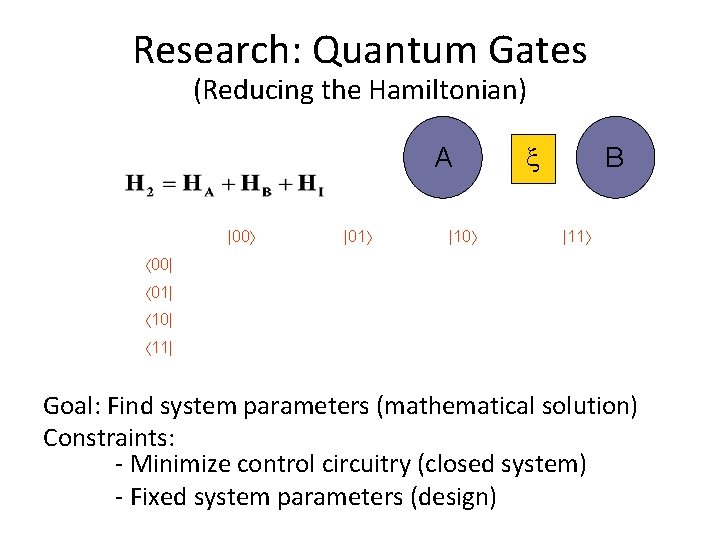
Research: Quantum Gates (Reducing the Hamiltonian) A |00 |01 |10 B |11 00| 01| 10| 11| Goal: Find system parameters (mathematical solution) Constraints: - Minimize control circuitry (closed system) - Fixed system parameters (design)

Research: “Controlled” Gates (Reducing the Hamiltonian) |00 00| |01 Similar to |10 |11 01| 10| 11| Fix A’s state – large A – can neglect effect of A. |00 00| 01| 10| 11| |01 |10 |11

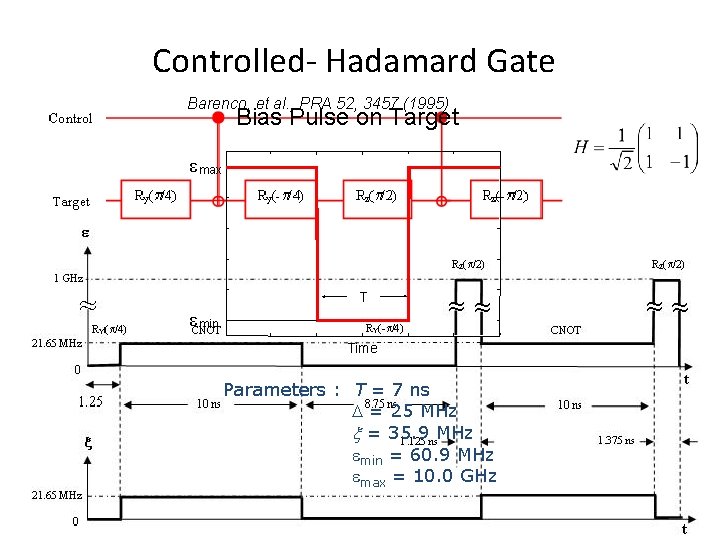
Controlled- Hadamard Gate Barenco, et al. , PRA 52, 3457 (1995) Bias Pulse on Target max T min Time Parameters : T = 7 ns = 25 MHz = 35. 9 MHz min = 60. 9 MHz max = 10. 0 GHz

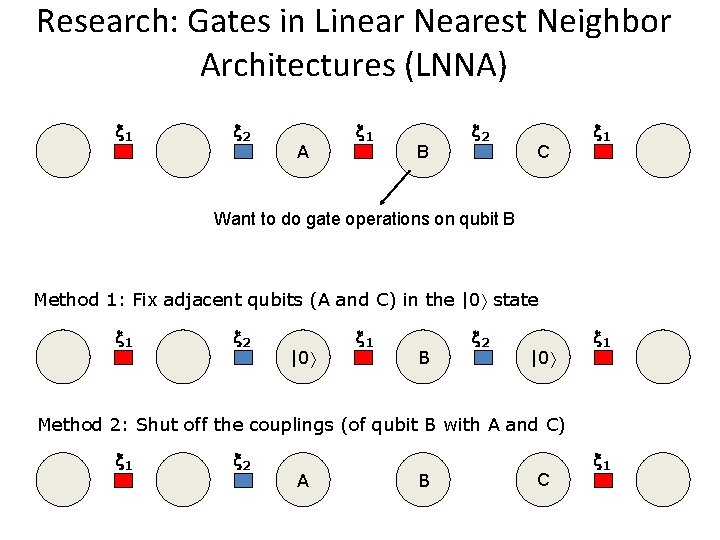
Research: Gates in Linear Nearest Neighbor Architectures (LNNA) 1 2 A 1 B 2 C 1 Want to do gate operations on qubit B Method 1: Fix adjacent qubits (A and C) in the |0 state 1 2 |0 1 B 2 |0 1 Method 2: Shut off the couplings (of qubit B with A and C) 1 2 A B C 1

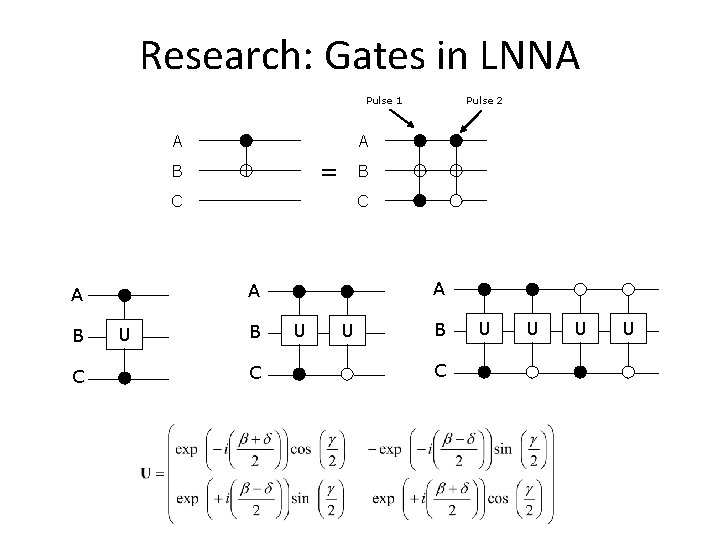
Research: Gates in LNNA Pulse 1 A A = B B C C A A A U Pulse 2 B C U U U U

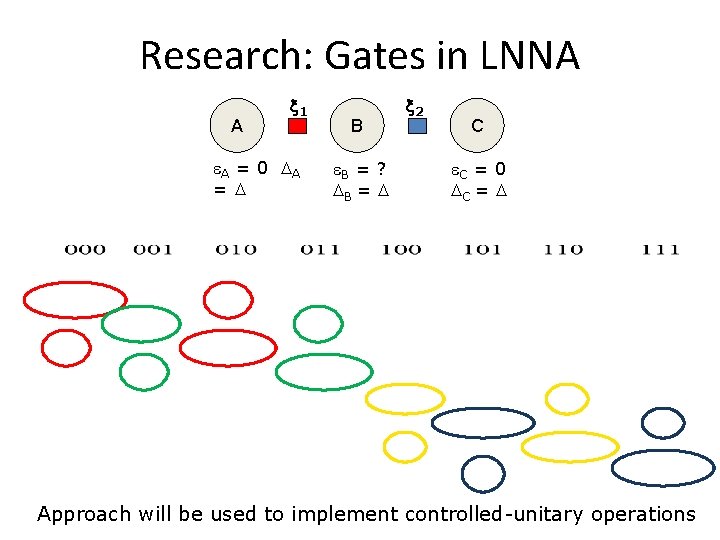
Research: Gates in LNNA A 1 A = 0 A = B B = ? B = 2 C C = 0 C = Approach will be used to implement controlled-unitary operations

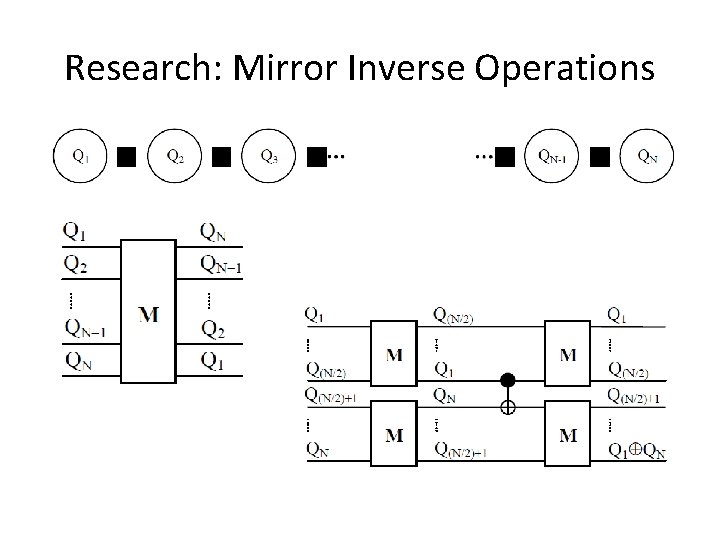
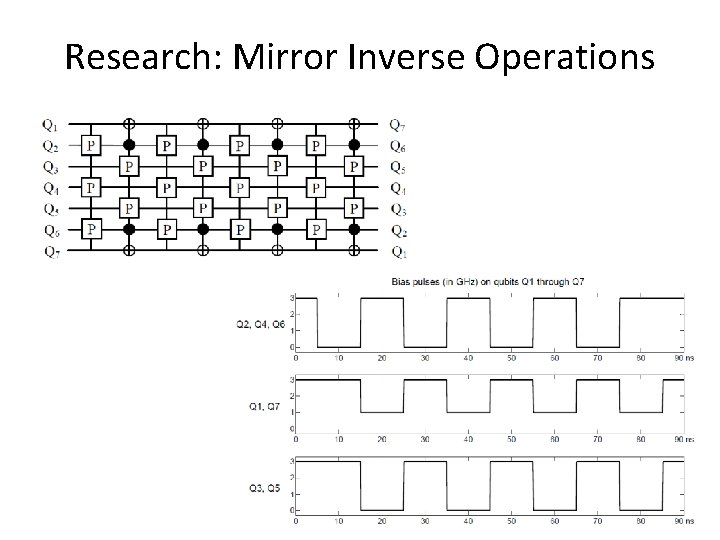
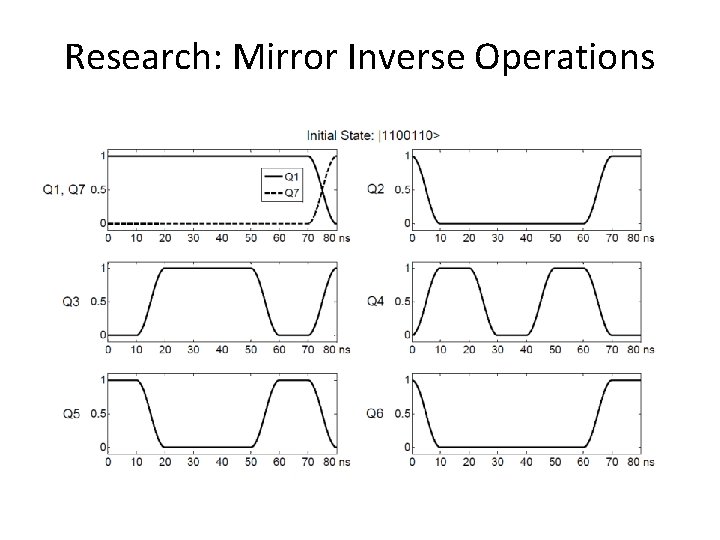
Research: Mirror Inverse Operations

Research: Mirror Inverse Operations

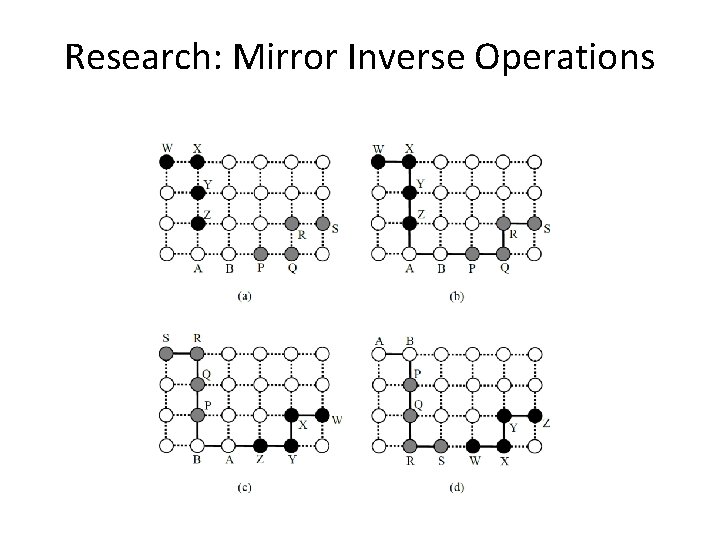
Research: Mirror Inverse Operations

Research: Mirror Inverse Operations

Current Research • Adiabatic Quantum Computing - optimization problems - hardware exists (DWave Systems) • Quantum Neural Networks - designing QNNs (exploit quantum phenomena) - using QNNs for different applications to calculate parameters • Fault-tolerant Quantum Computing - gate design without decoding