Quantum Computing Lessons in Physics and Metaphysics Andrew

Quantum Computing: Lessons in Physics and Metaphysics Andrew M. Steane Official Fellow, Exeter College Professor of Physics, Oxford University

Quantum Computing The Laws of Nature, or How everything works Computers and how they work

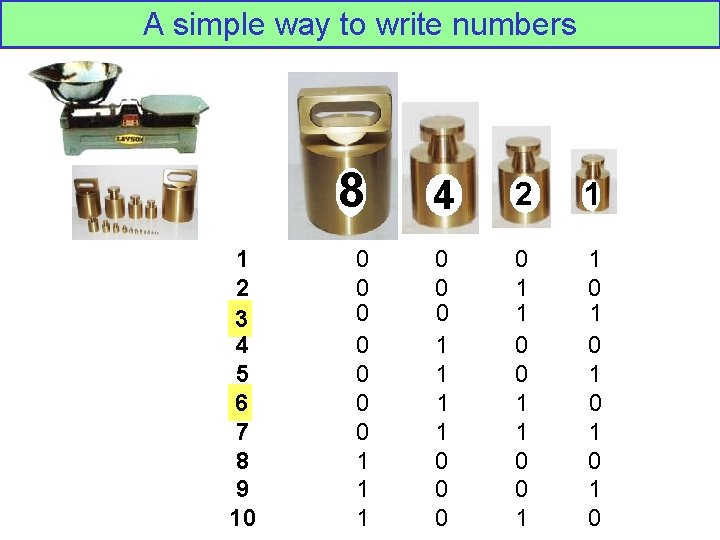
A simple way to write numbers 1 2 3 4 5 6 7 8 9 10 8 4 2 1 0 0 0 0 1 1 1 0 0 0 1 1 0 0 1 1 0 1 0 1 0

Expressing information using binary numbers red 1, orange 2, yellow 3 green 4, blue 5, indigo 6, violet 7 Picture = (1, 1, 5), (2, 1, 5), (3, 1, 5) … … (120, 130, 1), (121, 130, 1), (122, 130, 4) …

Expressing information using binary numbers 11110000010 1 111001 10000010 1 …

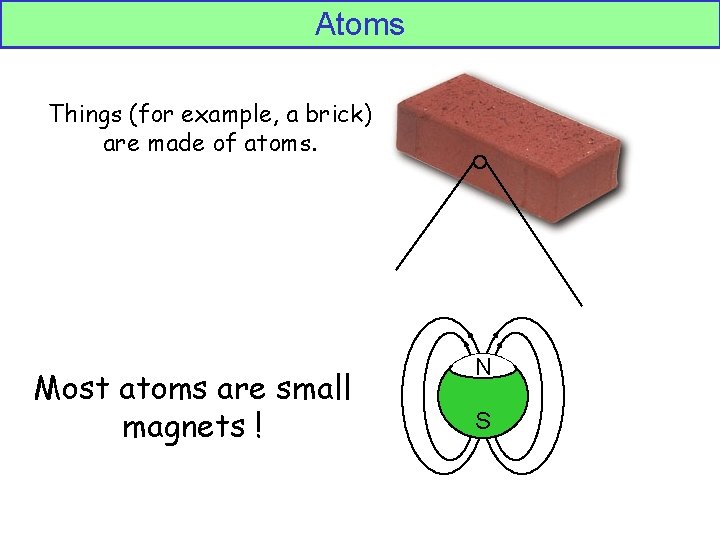
Atoms Things (for example, a brick) are made of atoms. Most atoms are small magnets ! N S

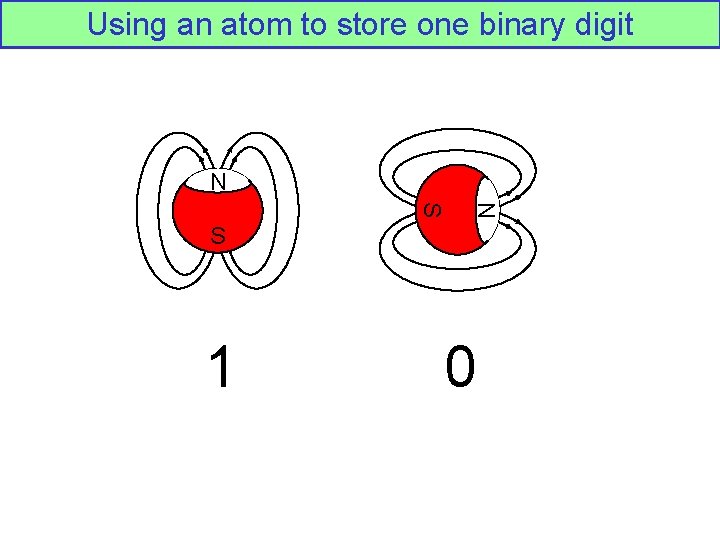
Using an atom to store one binary digit N N S S 1 0

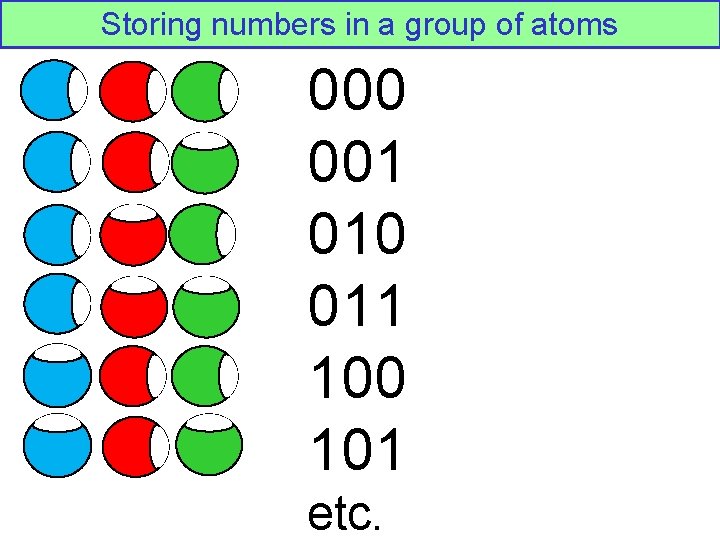
Storing numbers in a group of atoms 000 001 010 011 100 101 etc.

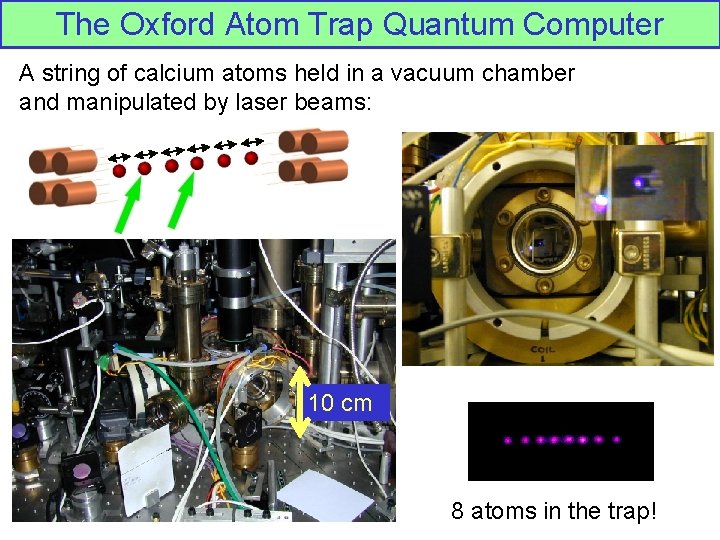
The Oxford Atom Trap Quantum Computer A string of calcium atoms held in a vacuum chamber and manipulated by laser beams: 10 cm 8 atoms in the trap!

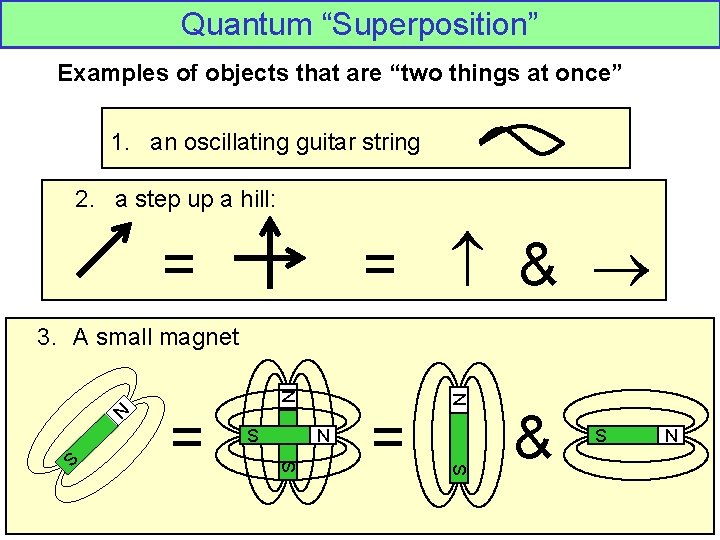
Quantum “Superposition” Examples of objects that are “two things at once” 1. an oscillating guitar string 2. a step up a hill: = & = S N = S S N 3. A small magnet & S N

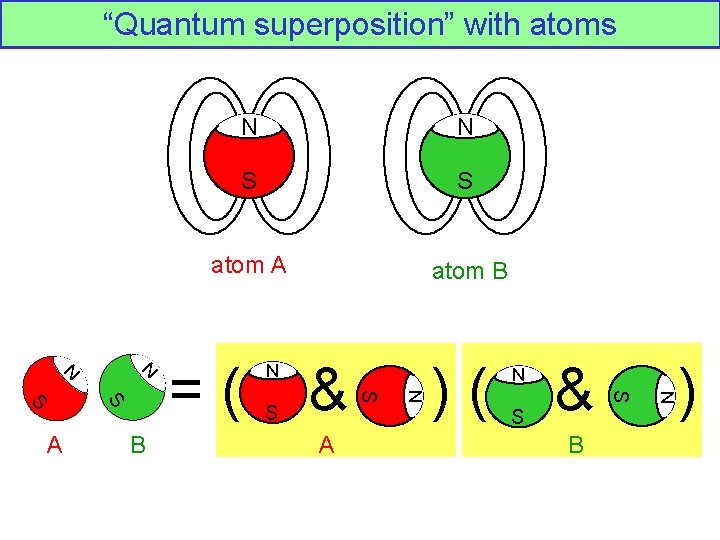
“Quantum superposition” with atoms N N S S atom A atom B & A )( S & B N S =( N N B N S S S A N )

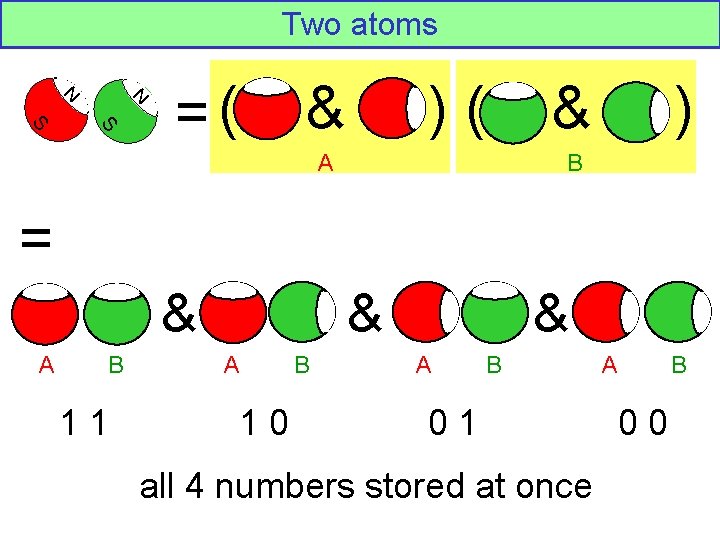
Two atoms N N S S =( & )( & A ) B = & A B 11 & A 10 B & A B 01 all 4 numbers stored at once A B 00

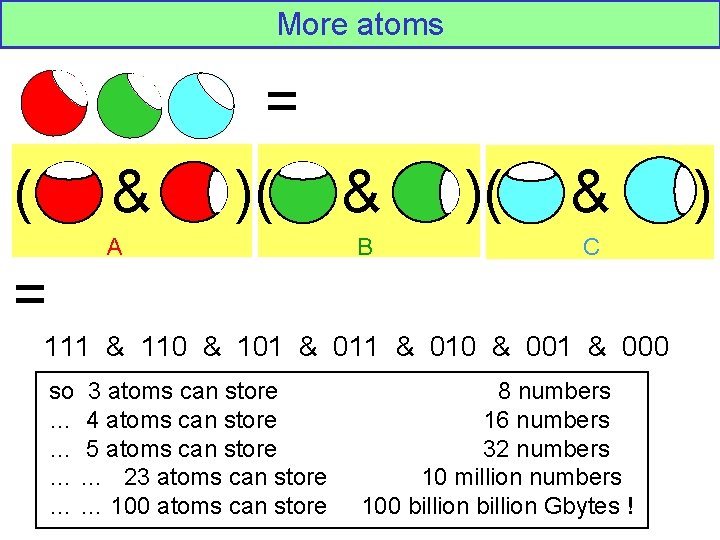
More atoms = ( & )( A & B )( & C = 111 & 110 & 101 & 010 & 001 & 000 so 3 atoms can store … 4 atoms can store … 5 atoms can store … … 23 atoms can store … … 100 atoms can store 8 numbers 16 numbers 32 numbers 10 million numbers 100 billion Gbytes ! )

Quantum computers are fast at some calculations 24 17 6 3 24 17 6 3 18 9 2 65 72 45 7 8 12 22 28 36 47 55 27 51 64 1 81 98 32 41 74 5 19 23 33 25 37 52 63 83 92 16 31 43 87 72 73 91 31 14 11 4 38 1 20 3 13 10 15 25 18 26 30 29 34 42 35 37 39 61 71 46 90 48 49 53 56 86 62 21 27 34 24 17 6 3 18 9 2 65 72 45 7 8 12 22 28 36 47 55 27 51 64 1 81 98 32 41 74 5 19 23 33 25 37 52 63 83 92 16 31 43 87 72 73 91 31 14 11 4 38 1 20 3 13 10 15 25 18 26 30 29 34 42 35 Repeats every 78 numbers

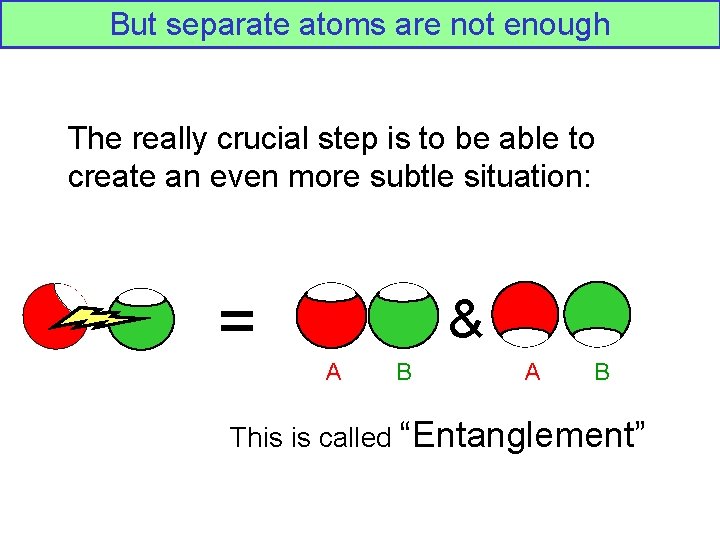
But separate atoms are not enough The really crucial step is to be able to create an even more subtle situation: = & A B This is called “Entanglement”

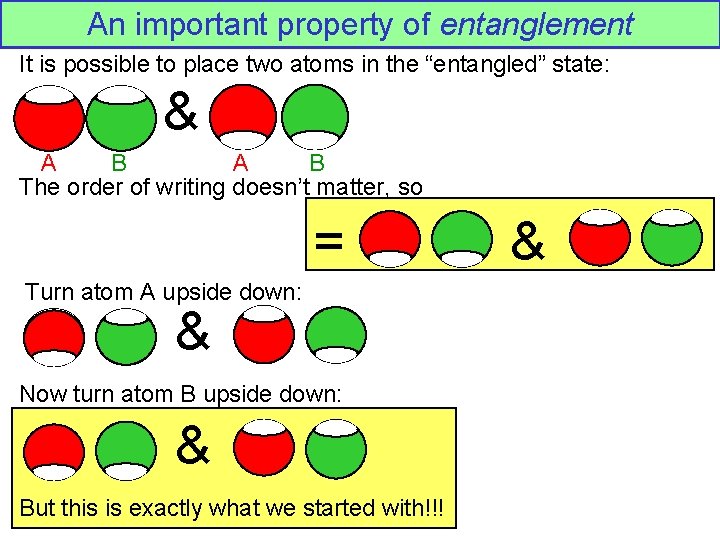
An important property of entanglement It is possible to place two atoms in the “entangled” state: & A B The order of writing doesn’t matter, so = Turn atom A upside down: & Now turn atom B upside down: & But this is exactly what we started with!!! &

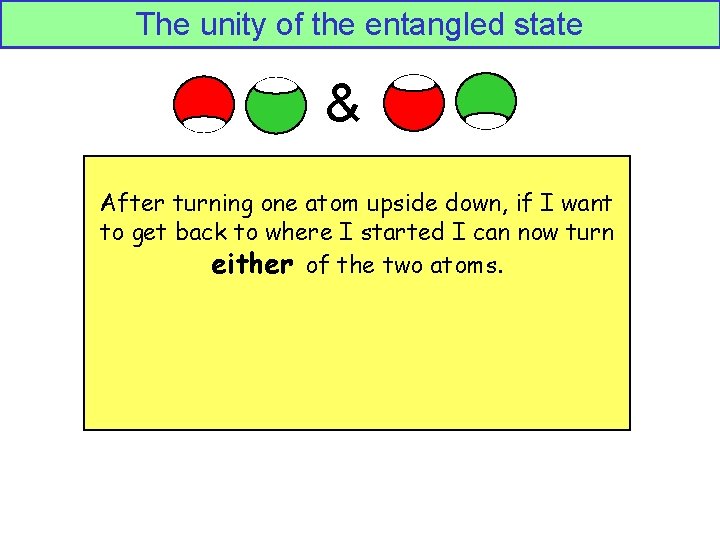
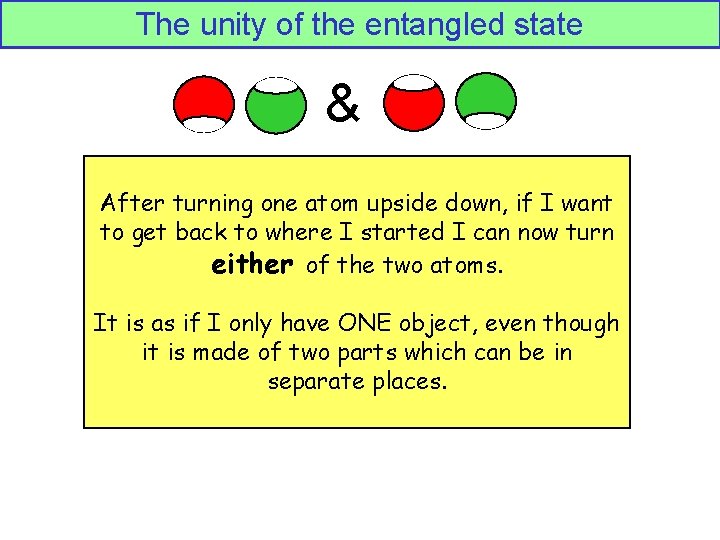
The unity of the entangled state & After turning one atom upside down, if I want to get back to where I started I can now turn either of the two atoms.

The unity of the entangled state & After turning one atom upside down, if I want to get back to where I started I can now turn either of the two atoms. It is as if I only have ONE object, even though it is made of two parts which can be in separate places.

REDUCTIONISM = “understand the parts that make up an object or system, and you will understand the whole”

REDUCTIONISM = “understand the parts that make up an object or system, and you will understand the whole” = the assumption of all science before ~1920, and almost all science to date But entanglement is simply not like this!

Some metaphysics • Entanglement is a physical property that does not fit with the concept of reductionism. • It is found throughout physics. • It makes the idea of an isolated system undefined. Physics cannot describe such a system, it can only describe relationships. • It is unclear how this extends to considerations of the cosmos as a whole.

What I didn’t tell you Most financial and diplomatic transactions done in the world today derive their security (i. e. confidentiality) from coding methods based on a repeat sequence method which a quantum computer can break …. Fortunately, quantum mechanics also provides new methods that allow truly unbreakable codes. However, the most interesting scientific and commercial application of quantum computers is to calculate how matter and molecules behave … possible impact on pharmaceuticals etc. The other thing I learn from all this is how subtle and wonderful the world is.

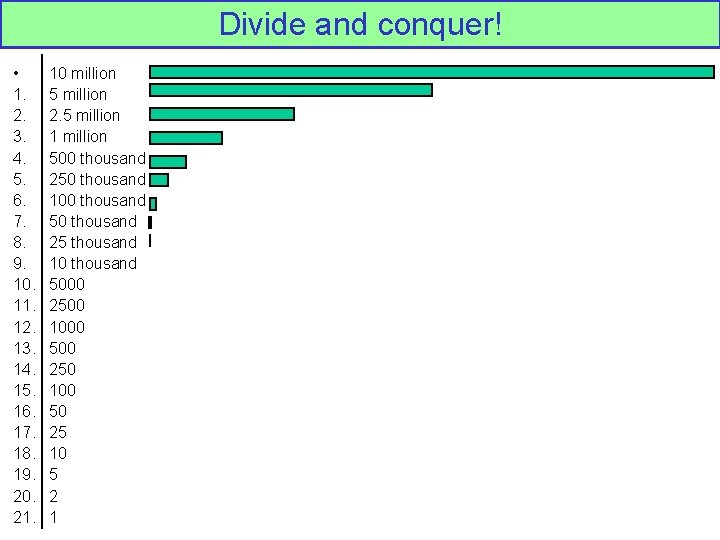
Speed of computer programs Searching for a name in a list (e. g. telephone directory) 1. Looking for a number when you don’t know the name (slow!) Look at every number from the beginning: 764832, 236122, 655891, . . . 2. Looking for a name (fast!) Jump in half way, decide which half to keep, then divide that in half, etc. Matthews; Smith; Patterson; . . . For 10 numbers in the list: takes a few seconds. For 10 names in the list: takes a few seconds. For 10 million numbers: takes about 5 million seconds (i. e. several months). For 10 million names: takes about 21 goes (less than a minute).

Divide and conquer! • 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 10 million 5 million 2. 5 million 1 million 500 thousand 250 thousand 100 thousand 50 thousand 25 thousand 10 thousand 5000 2500 1000 500 250 100 50 25 10 5 2 1

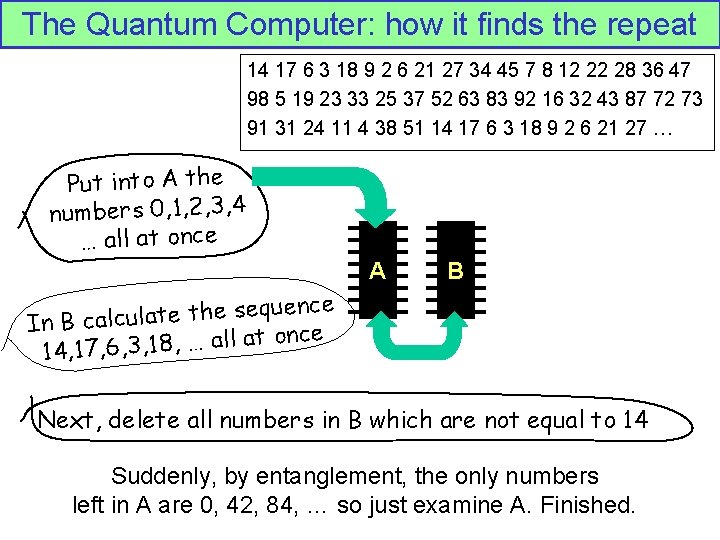
The Quantum Computer: how it finds the repeat 14 17 6 3 18 9 2 6 21 27 34 45 7 8 12 22 28 36 47 98 5 19 23 33 25 37 52 63 83 92 16 32 43 87 72 73 91 31 24 11 4 38 51 14 17 6 3 18 9 2 6 21 27 … Put into A the numbers 0, 1, 2, 3, 4 … all at once A B e c n e u q e s e h t e t In B calcula once t a ll a … , 8 , 1 , 3 14, 17, 6 Next, delete all numbers in B which are not equal to 14 Suddenly, by entanglement, the only numbers left in A are 0, 42, 84, … so just examine A. Finished.

Physics

How can computers do so many different things?

Expressing information using numbers “The quantum computer is very interesting. ” a 1, b 2, c 3: 20 8 5 0 17 21 1 14 20 21 13 0 3 15 13 16 21 … red 1, orange 2, yellow 3 green 4, blue 5, indigo 6, violet 7 Picture = (1, 1, 5), (2, 1, 5), (3, 1, 5) … … (130, 80, 1), (131, 80, 1), (132, 80, 4) …

2012 Nobel Prize in Physics Serge Haroche, David Wineland "for ground-breaking experimental methods that enable measuring and manipulation of individual quantum systems"

Oxford Ion Trap 2002 -03 The people who QIPC make summary, it go (sometimes) Faculty: Derek Stacey, Andrew Steane, David Lucas. Post-docs: Matt Mc. Donnell, (Angel Ramos) Marek Šašura. Post-grads: Jonathan Home, Simon Webster. Past students: J-P Stacey, Charles Donald, David Stevens. the trap

Developing microfabricated components. . . State of the art: Full, accurate manipulation of just 8 “quantum bits”. More limited manipulation of larger systems. QC in research labs in perhaps a decade or two?