Quantum Computers Algorithms and applications Simulating classical operations

Quantum Computers Algorithms and applications

Simulating classical operations Dušan Gajević 2/41

Simulating classical operations • Is it possible to simulate classical computer operations on a quantum computer? – Pure states correspond to classical bits – To implement any classical computer operation a universal set of gates is needed – (NOT, AND), (NOT, OR), (NAND), (NOR)… • Quantum computers are reversible, yet, in any of these sets there is at least one irreversible operation • Obviously, the real question is, can a reversible computer simulate an irreversible operation? Dušan Gajević 3/41

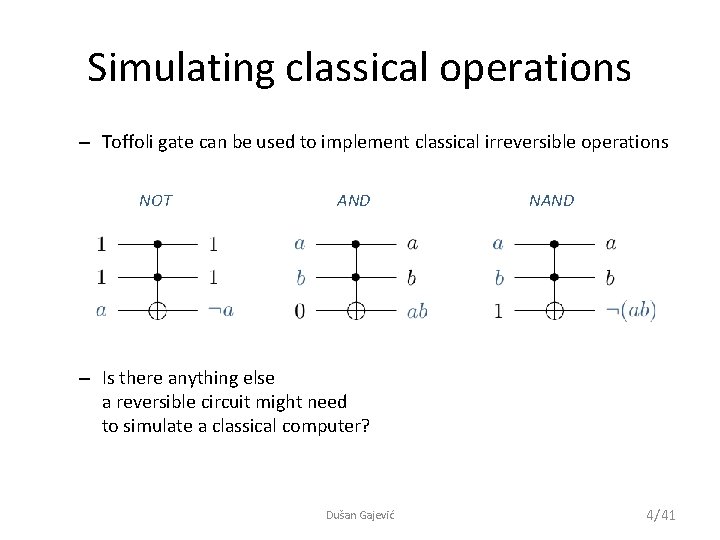
Simulating classical operations – Toffoli gate can be used to implement classical irreversible operations NOT AND NAND – Is there anything else a reversible circuit might need to simulate a classical computer? Dušan Gajević 4/41

Simulating classical operations – In fact, classical computer contains two more “gates” (elements) that are easily overlooked FANOUT ERASE – Using Toffoli gate Even a type of erase… …but not the actual ERASE Dušan Gajević 5/41

Simulating classical operations – In reversible computing, it is allowed to erase duplicates of information, but it is not allowed to erase the last copy • It is possible to simulate any classical irreversible computation using only Toffoli gates, but it requires a use of some extra bits • Put another way, Toffoli gate is a universal gate for classical reversible computing Dušan Gajević 6/41

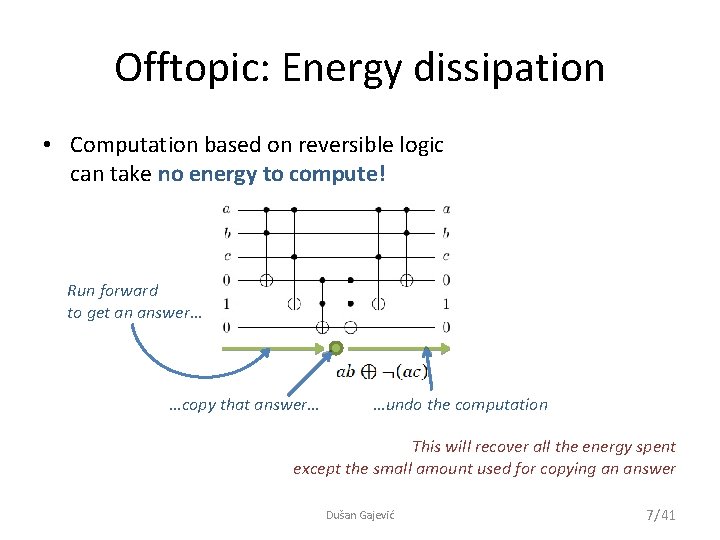
Offtopic: Energy dissipation • Computation based on reversible logic can take no energy to compute! Run forward to get an answer… …copy that answer… …undo the computation This will recover all the energy spent except the small amount used for copying an answer Dušan Gajević 7/41

Offtopic: Energy dissipation – Energy must be dissipated to initialize the system or to make a permanent record of an answer • These operations set a new value in a memory register regardless of what the state was, hence, they are irreversible Dušan Gajević 8/41

Simulating classical operations • We saw it’s possible to simulate irreversible operations on a reversible computer • Hence, it is possible to simulate classical operations on a quantum computer – But this is not what quantum computers are intended for – it is not much of a benefit… Dušan Gajević 9/41

Quantum parallelism Dušan Gajević 10/41

Quantum parallelism • A fundamental feature of many quantum algorithms – Suppose a binary function f(x) single bit in – single bit out – Let’s introduce a following unitary transformation XOR (addition modulo 2) Dušan Gajević 11/41

Quantum parallelism – And use it in a following circuit As if f(x) is evaluated for 2 values of x simultaneously …state after applying the introduced transformation Dušan Gajević 12/41

Quantum parallelism – Now a modified binary function f(x) single bit output n-bit input – and a corresponding unitary transformation Dušan Gajević 13/41

Quantum parallelism – in a modified circuit Hadamard transform – applied on n qubits Dušan Gajević 14/41

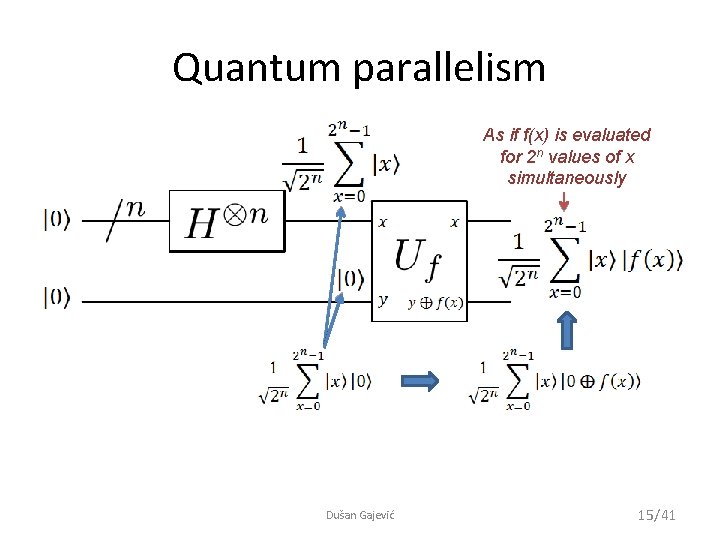
Quantum parallelism As if f(x) is evaluated for 2 n values of x simultaneously Dušan Gajević 15/41

Quantum parallelism • To achieve this sort of parallelism in classical computing multiple circuits are needed, while here a single circuit is employed – but, after measurement, only one evaluation of f(x) remains • Quantum computing requires more than quantum parallelism alone to work Dušan Gajević 16/41

“I do not like it, and I am sorry I had anything to do with it” – Erwin Schrödinger Dušan Gajević 17/41

Deutsch-Jozsa algorithm Dušan Gajević 18/41

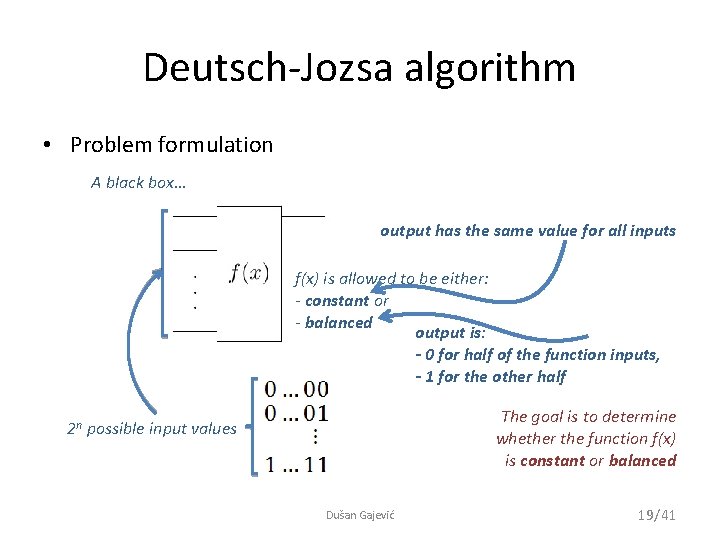
Deutsch-Jozsa algorithm • Problem formulation A black box… output has the same value for all inputs f(x) is allowed to be either: - constant or - balanced output is: - 0 for half of the function inputs, - 1 for the other half The goal is to determine whether the function f(x) is constant or balanced 2 n possible input values Dušan Gajević 19/41

Deutsch-Jozsa algorithm • Classical solution: – We are checking the output for every possible input value • If we come across a different output – we know the function is balanced • Otherwise, when we check at least half plus one possible inputs to be equal (2 n/2 + 1) – we know the function is constant • Time complexity of the classical solution is exponential Dušan Gajević 20/41

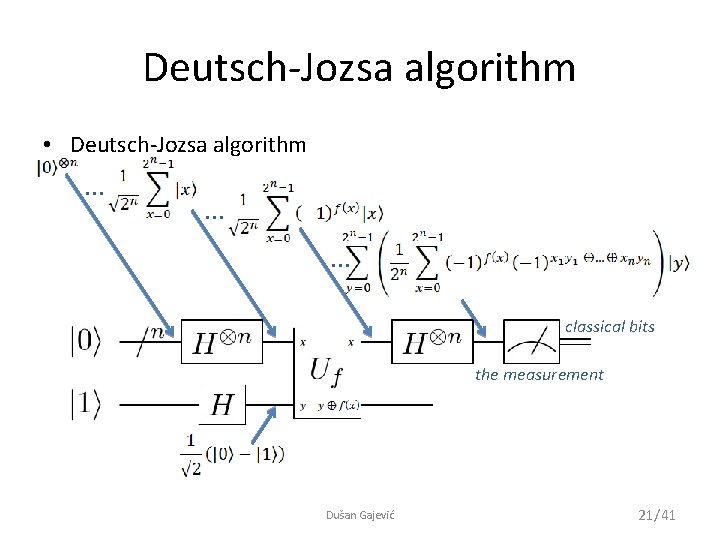
Deutsch-Jozsa algorithm • Deutsch-Jozsa algorithm … … … classical bits the measurement Dušan Gajević 21/41

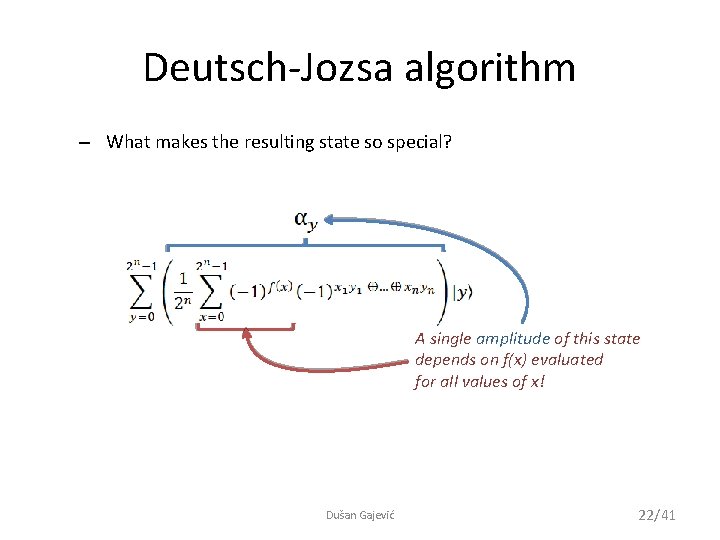
Deutsch-Jozsa algorithm – What makes the resulting state so special? A single amplitude of this state depends on f(x) evaluated for all values of x! Dušan Gajević 22/41

Deutsch-Jozsa algorithm – Of the special interest is the amplitude of the state Dušan Gajević 23/41

Deutsch-Jozsa algorithm – there are three different possibilities The function is constant f(x)=0 The function is constant f(x)=1 function constant results in 0… 0 The function is balanced half f(x)=1 – half f(x)=0 function balanced results in ≠ 0… 0 Dušan Gajević 24/41

Deutsch-Jozsa algorithm • Deutsch-Jozsa algorithm: – Compared to the classical solution displayed before, it offers exponential speedup – Unlike most quantum algorithms, it is deterministic – But it is of little practical use – it has no known applications • Nevertheless, it suggests quantum computers are capable of solving some problems much more efficiently than conventional computers Dušan Gajević 25/41

Factorization of large numbers Applications Dušan Gajević 26/41

Factorization of large numbers n digits prime numbers • The simplest solution is to start from 2 and check for every consequent number whether it’s a factor – Exponential time complexity • But even the best known classical algorithms have superpolynomial time complexity Dušan Gajević 27/41

Factorization of large numbers • The fact there is no computer today which could efficiently factor numbers is widely used in cryptography for secure data transmission (RSA public key routine) Dušan Gajević 28/41

Factorization of large numbers • Shor’s algorithm – in 1994, Peter Shor published a quantum algorithm for factoring large numbers – Like most quantum algorithms, it is non-deterministic – It has polynomial time complexity – Shor also published a polynomial-time quantum algorithm for discrete logarithms • These algorithms sparked a huge amount of interest in quantum computing Dušan Gajević 29/41

Quantum search Applications Dušan Gajević 30/41

Quantum search • Classically, and on average, how many operations are required for searching an unsorted database with N elements? • Grover’s algorithm – in 1996, Lov Grover formulated a quantum algorithm for searching an unstructured database in O(N 1/2) time – Another non-deterministic quantum algorithm Dušan Gajević 31/41

Quantum search • The quadratic speedup might not look impressive compared to exponential speedup offered by algorithms based on quantum Fourier transform – But for large search spaces… • Quantum search algorithms, also, have a wider range of application than algorithms based on quantum Fourier transformation Dušan Gajević 32/41

Quantum simulation Applications Dušan Gajević 33/41

Quantum simulation • Simulation of naturally occurring quantum systems – another possible application of quantum computers • Why are classical computers so bad at simulating quantum systems? – For a single qubit, a hydrogen atom, two complex coefficients are needed to specify the state of the system – For 2 hydrogen atoms, 4 complex coefficients are needed – For 3 atoms, 8 coefficients – … – For N atoms, 2 N coefficients Number grows exponentially! Dušan Gajević 34/41

Quantum simulation – For only 30 qubits, more than a billion complex coefficients are needed! Obviously, quantum systems are really good at spending classical resources • Amount of resources needed to simulate a quantum system on a quantum computer grows linearly with the growth of the number of simulated elements – But the extraction of desired information still poses a problem, due to collapse caused by measurement Dušan Gajević 35/41

Technical challenges Dušan Gajević 36/41

Quantum decoherence • There a lot of technical challenges in building a large-scale quantum computer • One of the greatest challenges is minimizing quantum decoherence – Quantum system can get entangled with the environment and evolve as if the environment “measured” the quantum system – Decoherence is irreversible, as it is non-unitary • Quantum systems have to be isolated as much as possible from its environment as any unintentional interaction with the outside world can disturb the fragile state of the system Dušan Gajević 37/41

Advances Dušan Gajević 38/41

Advances • In 2010, company named D-Wave Systems announced D-Wave One, the first commercially available quantum computer system – 128 -qubit quantum processor acting as a co-processor, accelerator • Intended for solving discrete optimization problems – Front-ended on a network as a standard server – Adiabatic model, unlike gate model explained earlier • Quantum annealing – Operating in an extreme environment – Low power consumption power demand expected to remain constant with scaling up Dušan Gajević 39/41

Advances • In 2013, D-Wave Systems launched 512 -qubit D-Wave Two • Price? • Controversy Dušan Gajević 40/41

References • • University of California, Berkeley, Qubits and Quantum Measurement and Entanglement, lecture notes, http: //www-inst. eecs. berkeley. edu/~cs 191/sp 12/ Michael A. Nielsen, Isaac L. Chuang, Quantum Computation and Quantum Information, Cambridge University Press, Cambridge, UK, 2010. Colin P. Williams, Explorations in Quantum Computing, Springer, London, 2011. Samuel L. Braunstein, Quantum Computation Tutorial, electronic document University of York, UK Bernhard Ömer, A Procedural Formalism for Quantum Computing, electronic document, Technical University of Vienna, Austria, 1998. Artur Ekert, Patrick Hayden, Hitoshi Inamori, Basic Concepts in Quantum Computation, electronic document, Centre for Quantum Computation, University of Oxford, UK, 2008. Wikipedia, the free encyclopedia, 2014. Dušan Gajević 41/41