Quantum Computer Implementations Christopher Monroe University of Michigan






















- Slides: 67

Quantum Computer Implementations Christopher Monroe University of Michigan Department of Physics http: //monroelab 2. physics. lsa. umich. edu/ US Advanced Research and Development Activity US National Security Agency US Army Research Office National Science Foundation

ENIAC (1946)

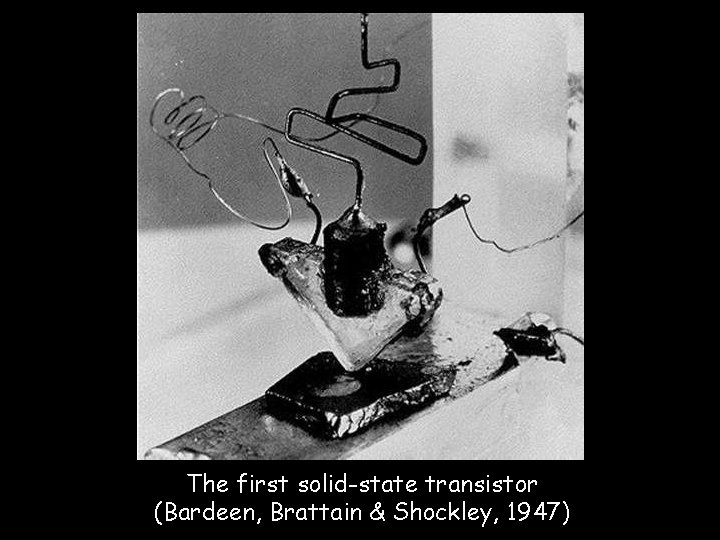
The first solid-state transistor (Bardeen, Brattain & Shockley, 1947)

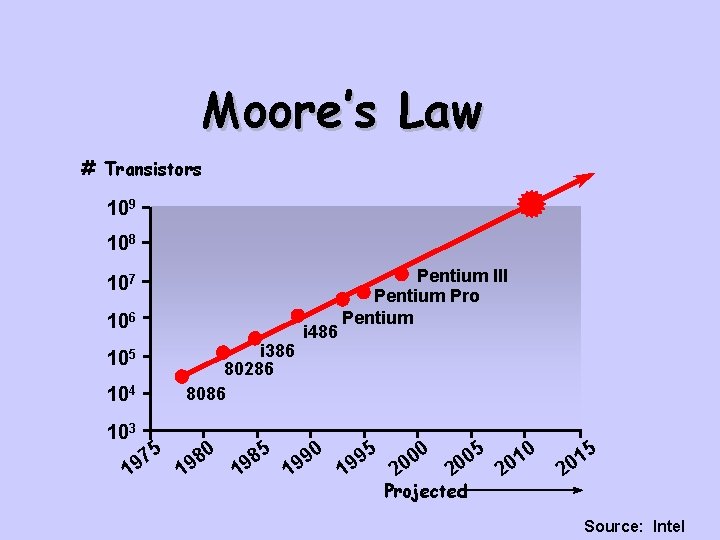
Moore’s Law # Transistors 109 108 107 106 i 386 80286 8086 105 104 103 5 7 9 1 0 8 9 1 5 i 486 0 9 9 1 Pentium III Pentium Pro Pentium 5 9 9 1 0 0 0 2 5 0 0 2 Projected 0 1 0 2 5 1 0 2 Source: Intel

“There's Plenty of Room at the Bottom” (1959 APS annual meeting) Richard Feynman “When we get to the very, very small world – say circuits of seven atoms - we have a lot of new things that would happen that represent completely new opportunities for design. Atoms on a small scale behave like nothing on a large scale, for they satisfy the laws of quantum mechanics…”

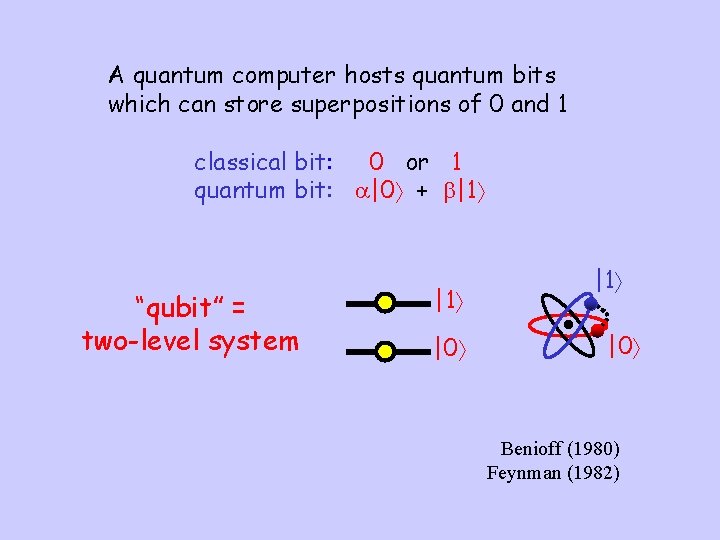
A quantum computer hosts quantum bits which can store superpositions of 0 and 1 classical bit: 0 or 1 quantum bit: |0 + |1 “qubit” = two-level system |1 |0 Benioff (1980) Feynman (1982)

GOOD NEWS… N qubits can store 2 N numbers simultaneously Example: N=3 qubits = a 0 |000 + a 1 |001 + a 2 |010 + a 3 |011 a 4 |100 + a 5 |101 + a 6 |110 + a 7 |111 …BAD NEWS… Measurement gives random result e. g. , |011

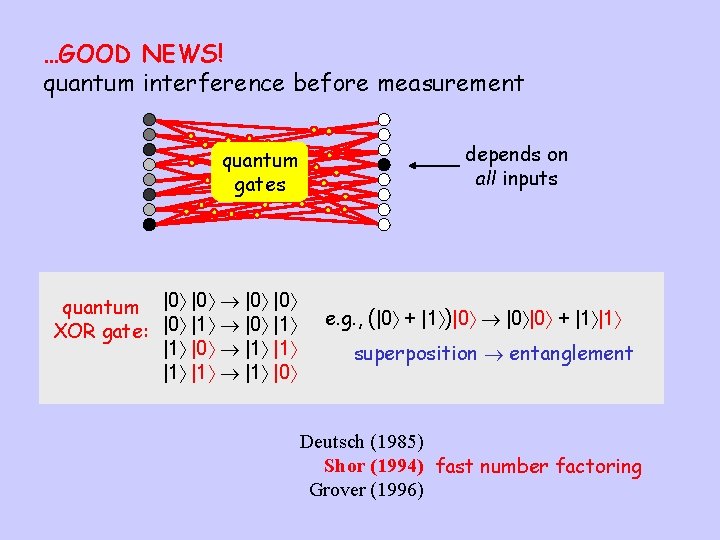
…GOOD NEWS! quantum interference before measurement quantum gates quantum |0 |0 XOR gate: |0 |1 |1 |0 |1 |1 |1 |0 depends on all inputs e. g. , (|0 + |1 )|0 |0 |0 + |1 |1 superposition entanglement Deutsch (1985) Shor (1994) fast number factoring Grover (1996)

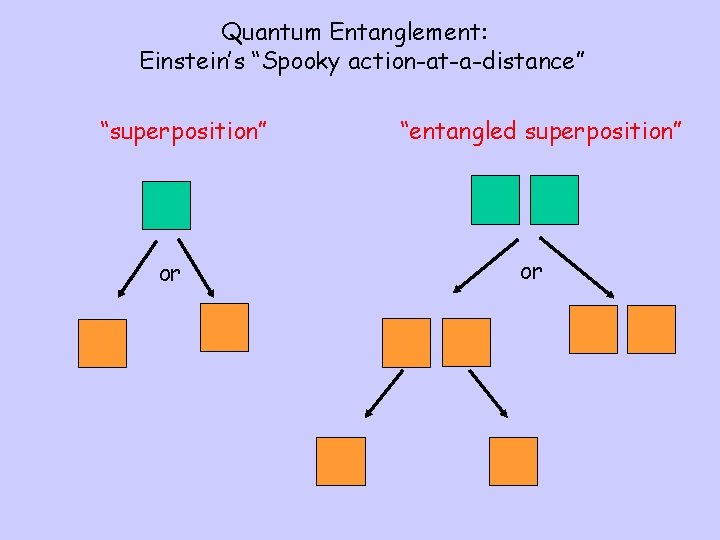
Quantum Entanglement: Einstein’s “Spooky action-at-a-distance” “superposition” or “entangled superposition” or


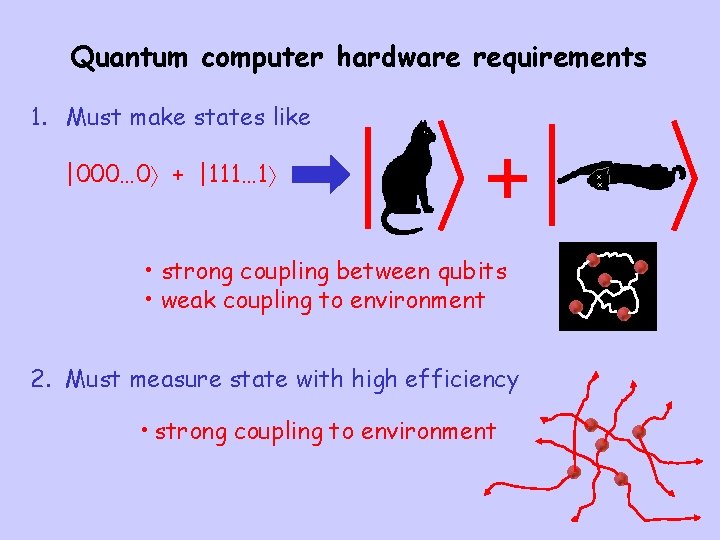
Quantum computer hardware requirements 1. Must make states like |000… 0 + |111… 1 + • strong coupling between qubits • weak coupling to environment 2. Must measure state with high efficiency • strong coupling to environment x x

Physical Implementations 1. Individual atoms and photons a. ion traps b. atoms in optical lattices c. photon downconversion and cavity-QED 2. Superconductors a. Cooper-pair boxes (charge qubits) b. rf-SQUIDS (flux qubits) 3. Semiconductors quantum dots 4. Other condensed-matter a. NMR b. electrons floating on liquid helium c. single phosphorus atoms in silicon

0. 3 mm

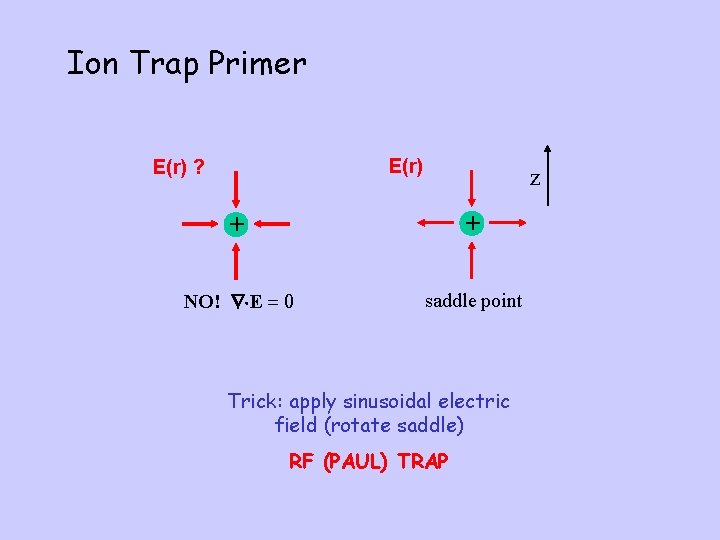
Ion Trap Primer E(r) ? z + + NO! E = 0 saddle point Trick: apply sinusoidal electric field (rotate saddle) RF (PAUL) TRAP

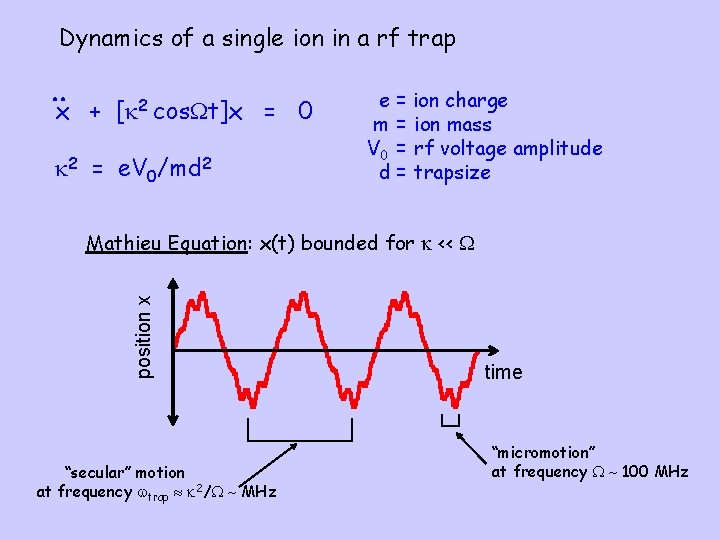
Dynamics of a single ion in a rf trap x + [k 2 cos. Wt]x = 0 k 2 = e. V 0/md 2 e = ion charge m = ion mass V 0 = rf voltage amplitude d = trapsize position x Mathieu Equation: x(t) bounded for k << W “secular” motion at frequency wtrap k 2/W MHz time “micromotion” at frequency W 100 MHz

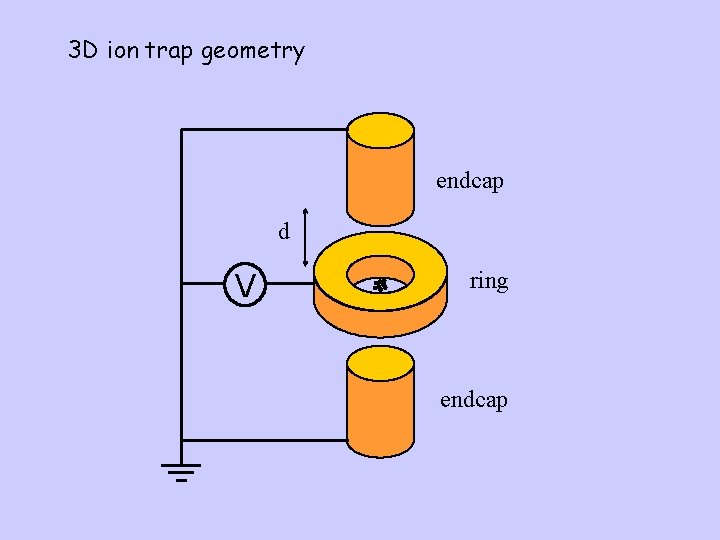
3 D ion trap geometry endcap d V ring endcap

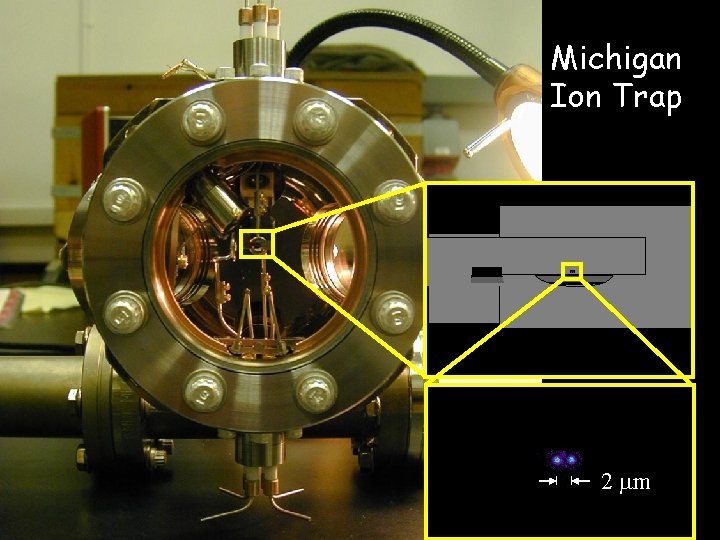
Michigan Ion Trap 2 mm

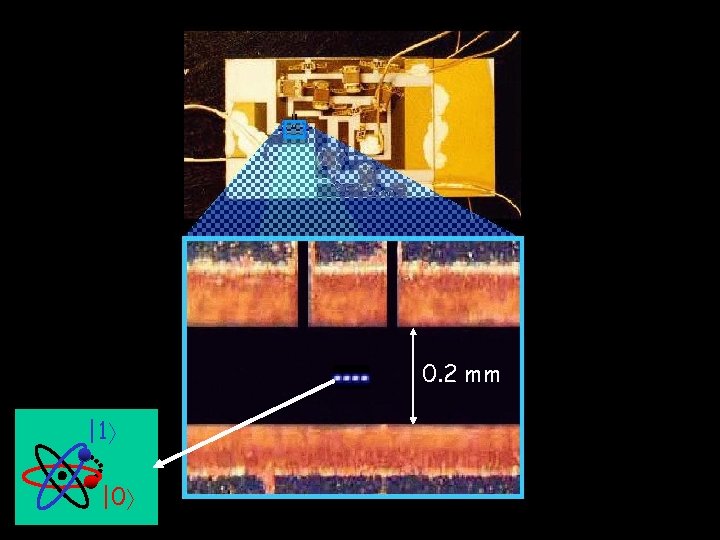
0. 2 mm |1 |0

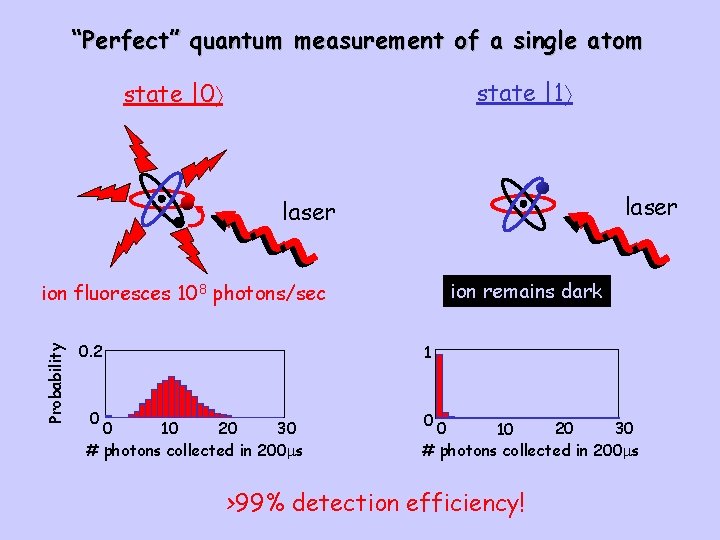
“Perfect” quantum measurement of a single atom state |1 state |0 laser ion remains dark Probability ion fluoresces 108 photons/sec 0. 2 1 0 0 0 10 20 30 # photons collected in 200 ms 0 20 30 10 # photons collected in 200 ms >99% detection efficiency!

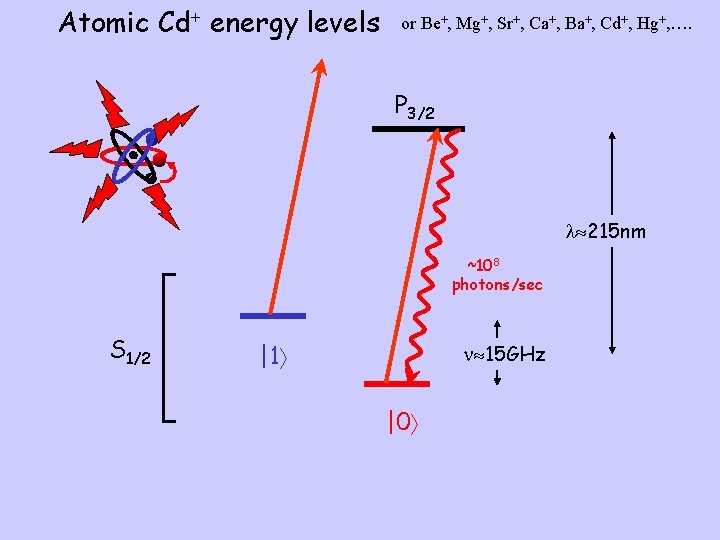
Atomic Cd+ energy levels or Be+, Mg+, Sr+, Ca+, Ba+, Cd+, Hg+, …. P 3/2 215 nm ~108 photons/sec S 1/2 |1 15 GHz |0

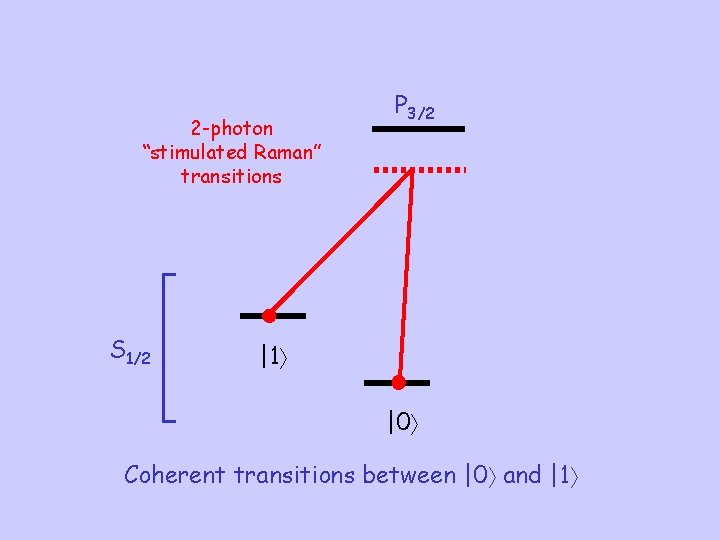
2 -photon “stimulated Raman” transitions S 1/2 P 3/2 |1 |0 Coherent transitions between |0 and |1

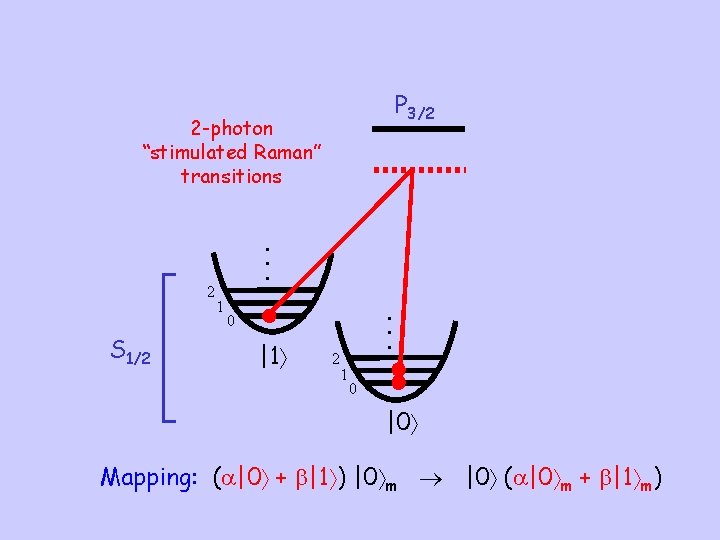
P 3/2 2 -photon “stimulated Raman” transitions 2 S 1/2 • • • 1 0 |1 2 1 • • • 0 |0 Mapping: ( |0 + |1 ) |0 m |0 ( |0 m + |1 m)

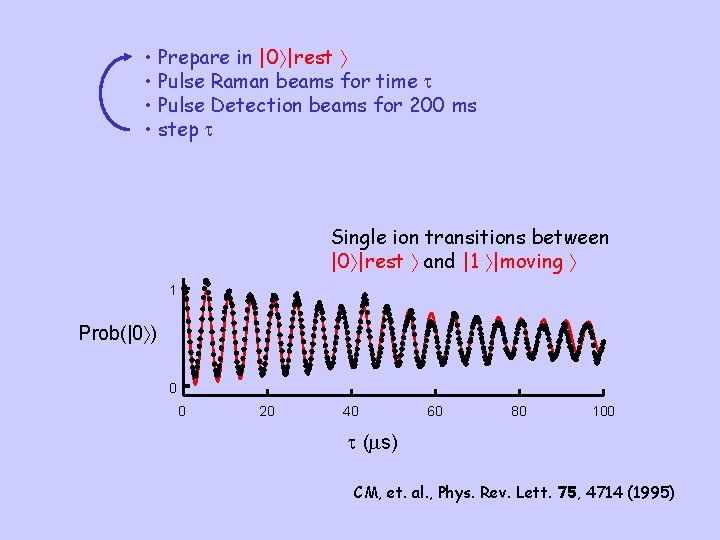
• Prepare in |0 |rest • Pulse Raman beams for time t • Pulse Detection beams for 200 ms • step t Single ion transitions between |0 |rest and |1 |moving 1 Prob(|0 ) 0 0 20 40 60 80 100 t (ms) CM, et. al. , Phys. Rev. Lett. 75, 4714 (1995)

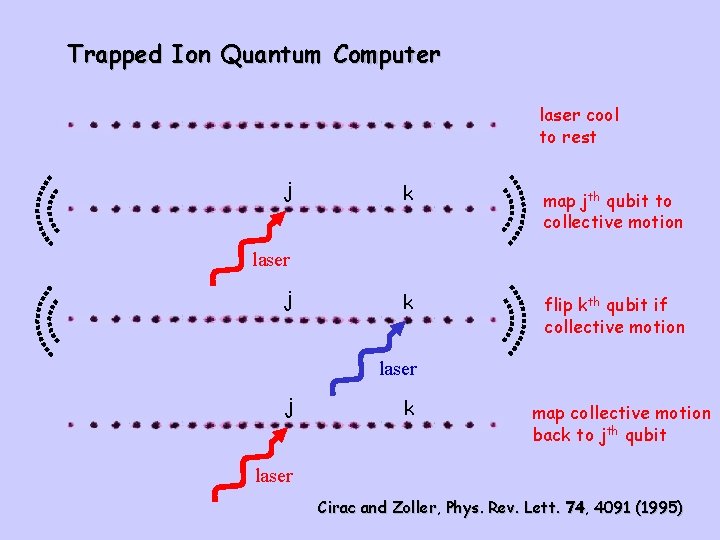
Trapped Ion Quantum Computer laser cool to rest j k map jth qubit to collective motion k flip kth qubit if collective motion laser j k map collective motion back to jth qubit laser Cirac and Zoller, Phys. Rev. Lett. 74, 4091 (1995)

State-of-the-art: Four-qubit quantum logic gate |0000 + eif|1111 Sackett, et al. , Nature 404, 256 (2000)



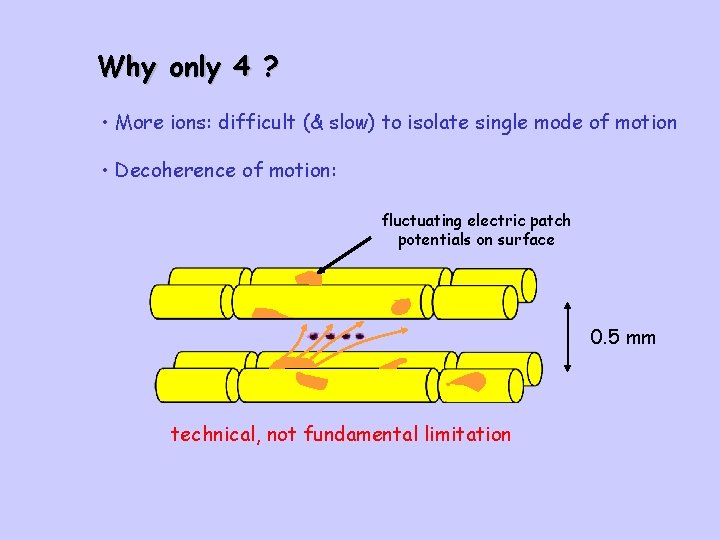
Why only 4 ? • More ions: difficult (& slow) to isolate single mode of motion • Decoherence of motion: fluctuating electric patch potentials on surface 0. 5 mm technical, not fundamental limitation

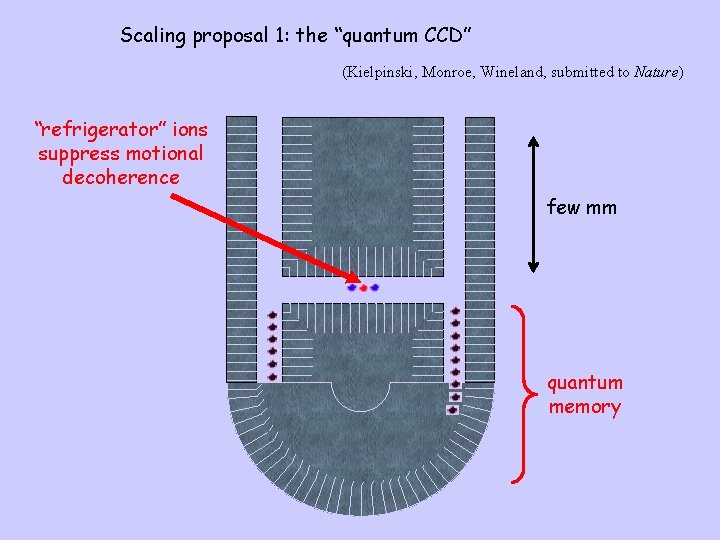
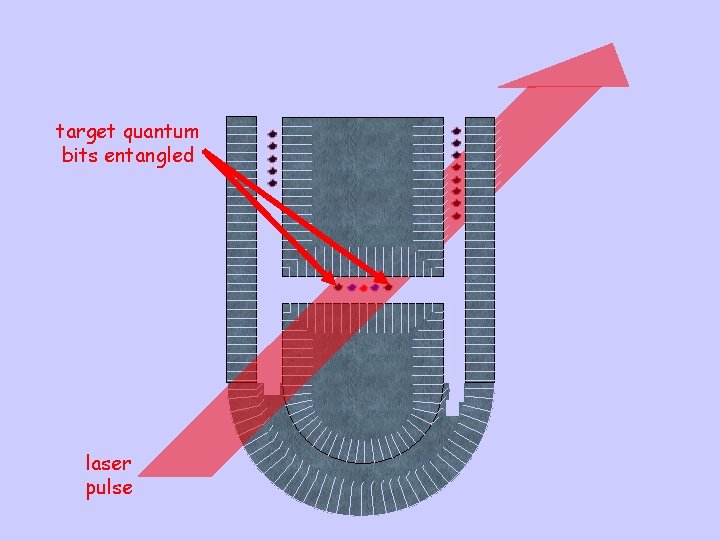
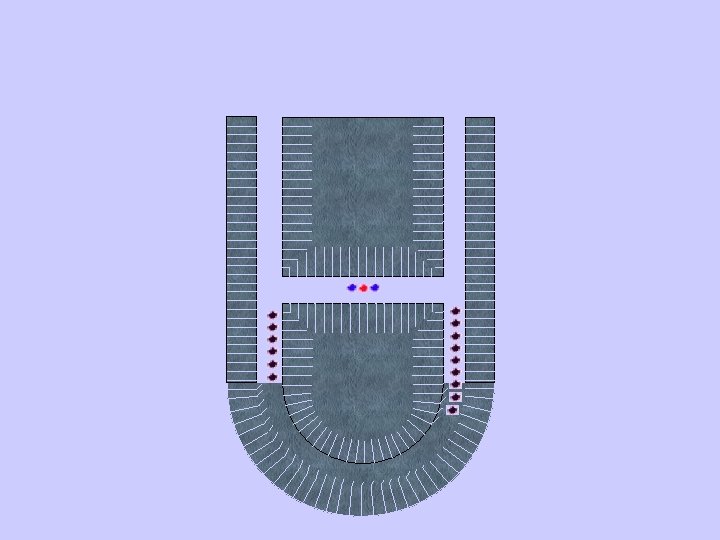
Scaling proposal 1: the “quantum CCD” (Kielpinski, Monroe, Wineland, submitted to Nature) “refrigerator” ions suppress motional decoherence few mm quantum memory

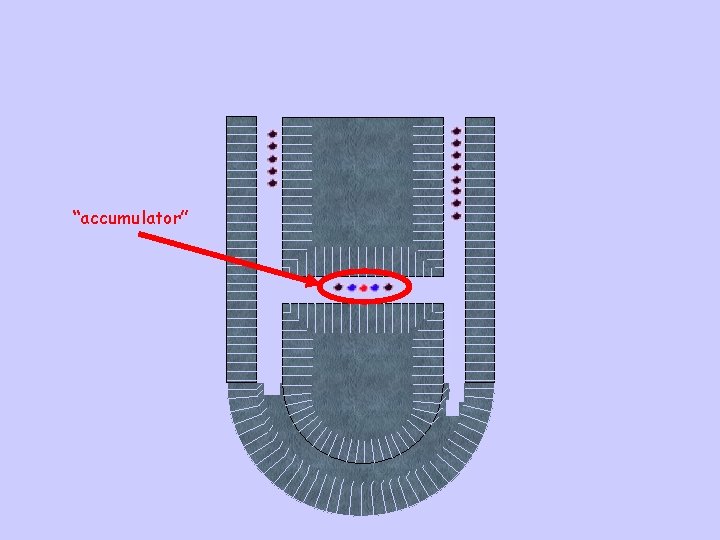
“accumulator”

target quantum bits entangled laser pulse


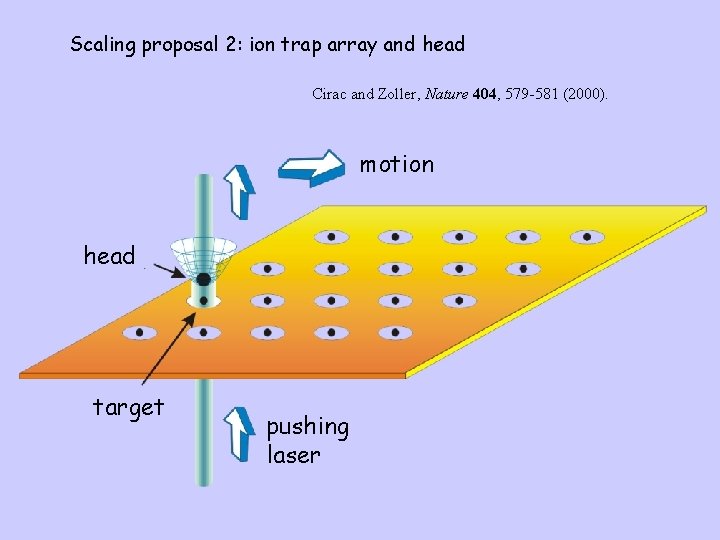
Scaling proposal 2: ion trap array and head Cirac and Zoller, Nature 404, 579 -581 (2000). motion head target pushing laser

Physical Implementations 1. Individual atoms and photons a. ion traps b. atoms in optical lattices c. photon downconversion and cavity-QED 2. Superconductors a. Cooper-pair boxes (charge qubits) b. rf-SQUIDS (flux qubits) 3. Semiconductors quantum dots 4. Other condensed-matter a. NMR b. electrons floating on liquid helium c. single phosphorus atoms in silicon

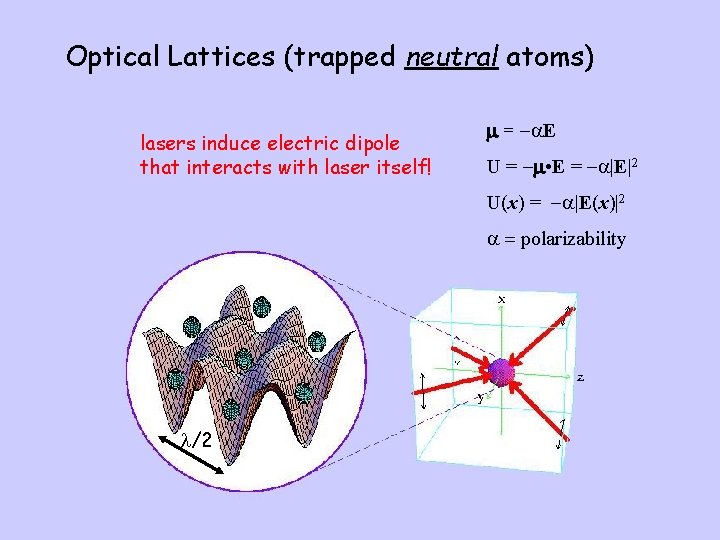
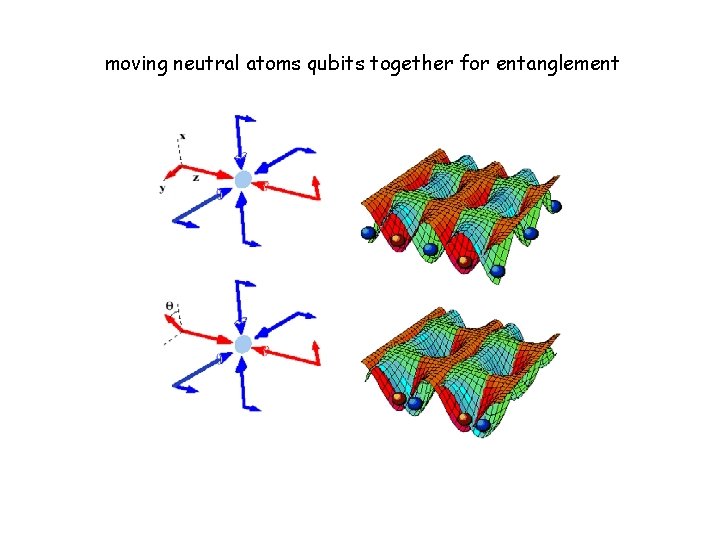
Optical Lattices (trapped neutral atoms) lasers induce electric dipole that interacts with laser itself! m = - E U = -m • E = - |E|2 U(x) = - |E(x)|2 = polarizability /2

moving neutral atoms qubits together for entanglement

Physical Implementations 1. Individual atoms and photons a. ion traps b. atoms in optical lattices c. photon downconversion and cavity-QED 2. Superconductors a. Cooper-pair boxes (charge qubits) b. rf-SQUIDS (flux qubits) 3. Semiconductors quantum dots 4. Other condensed-matter a. NMR b. electrons floating on liquid helium c. single phosphorus atoms in silicon

Individual photons qubit: |0 = zero photons |1 = one photon 50/50 weak laser A B send single photons | 1 = |0 A|1 B + |1 A|0 B Quantum Entanglement!

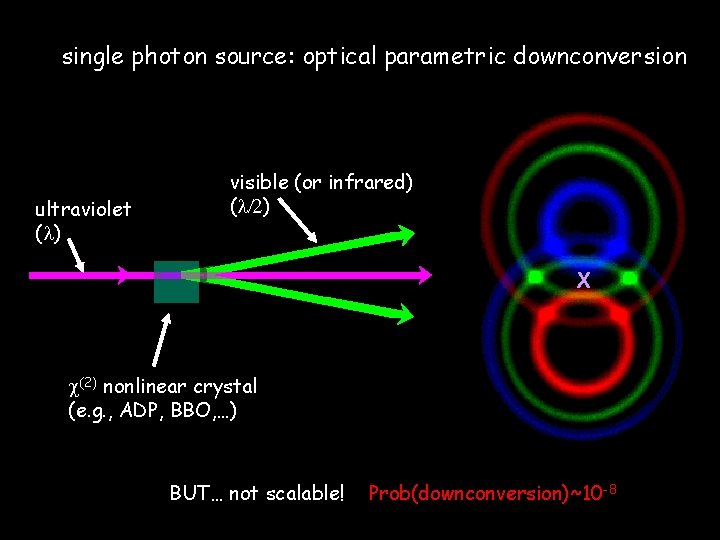
single photon source: optical parametric downconversion ultraviolet ( ) visible (or infrared) ( /2) X c(2) nonlinear crystal (e. g. , ADP, BBO, …) BUT… not scalable! Prob(downconversion)~10 -8

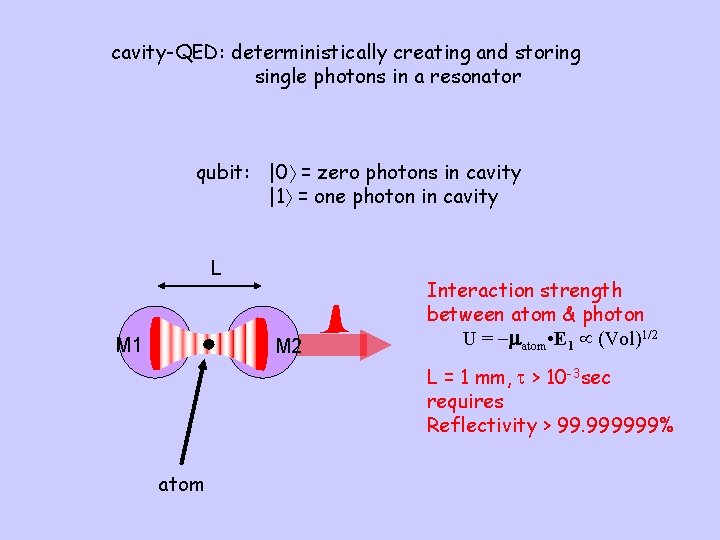
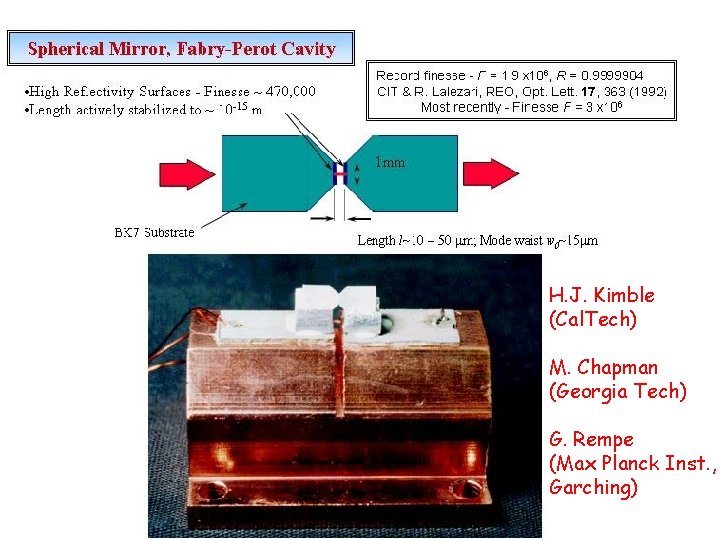
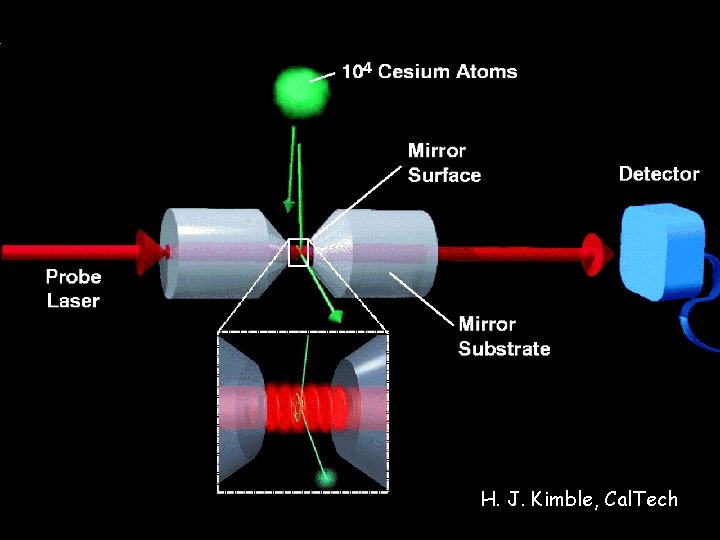
cavity-QED: deterministically creating and storing single photons in a resonator qubit: |0 = zero photons in cavity |1 = one photon in cavity L M 1 M 2 Interaction strength between atom & photon U = -matom • E 1 (Vol)1/2 L = 1 mm, t > 10 -3 sec requires Reflectivity > 99. 999999% atom

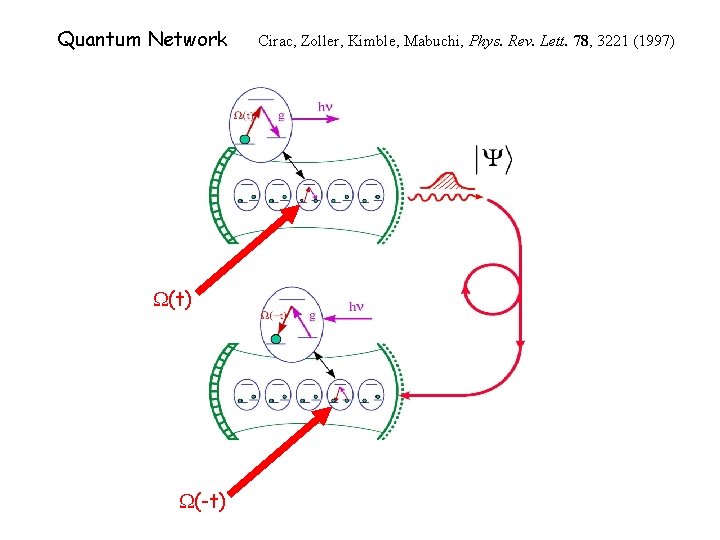
Quantum Network W(t) W(-t) Cirac, Zoller, Kimble, Mabuchi, Phys. Rev. Lett. 78, 3221 (1997)

H. J. Kimble (Cal. Tech) M. Chapman (Georgia Tech) G. Rempe (Max Planck Inst. , Garching)

H. J. Kimble, Cal. Tech

Physical Implementations 1. Individual atoms and photons a. ion traps b. atoms in optical lattices c. photon downconversion and cavity-QED 2. Superconductors a. Cooper-pair boxes (charge qubits) b. rf-SQUIDS (flux qubits) 3. Semiconductors quantum dots 4. Other condensed-matter a. NMR b. electrons floating on liquid helium c. single phosphorus atoms in silicon

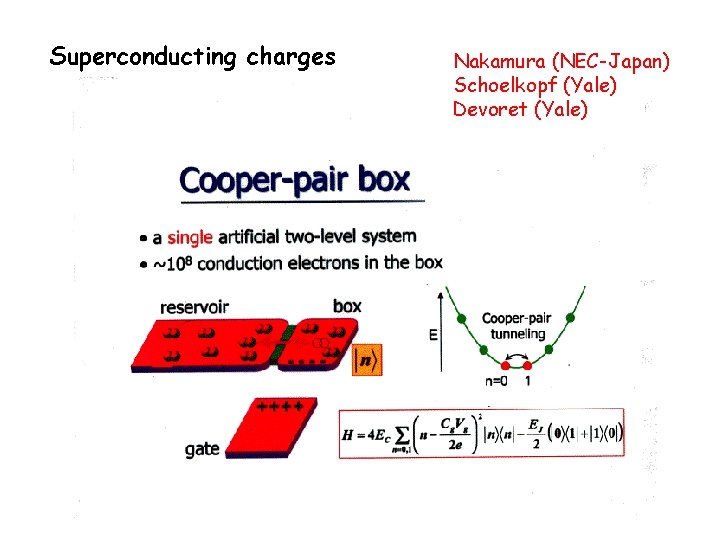
Superconducting charges Nakamura (NEC-Japan) Schoelkopf (Yale) Devoret (Yale)


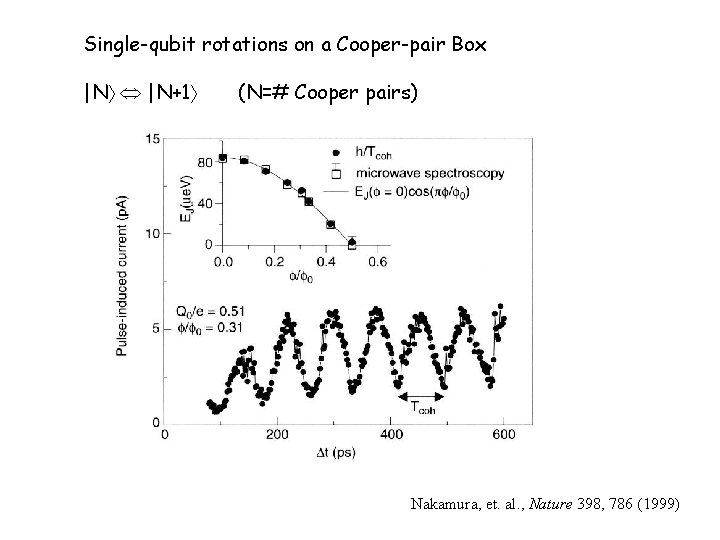
Single-qubit rotations on a Cooper-pair Box |N |N+1 (N=# Cooper pairs) Nakamura, et. al. , Nature 398, 786 (1999)

Physical Implementations 1. Individual atoms and photons a. ion traps b. atoms in optical lattices c. photon downconversion and cavity-QED 2. Superconductors a. Cooper-pair boxes (charge qubits) b. rf-SQUIDS (flux qubits) 3. Semiconductors quantum dots 4. Other condensed-matter a. NMR b. electrons floating on liquid helium c. single phosphorus atoms in silicon

Superconducting currents J. E. Mooij, … Science 285, 1036 (1999). quantized flux qubit states

Physical Implementations 1. Individual atoms and photons a. ion traps b. atoms in optical lattices c. photon downconversion and cavity-QED 2. Superconductors a. Cooper-pair boxes (charge qubits) b. rf-SQUIDS (flux qubits) 3. Semiconductors quantum dots 4. Other condensed-matter a. NMR b. electrons floating on liquid helium c. single phosphorus atoms in silicon

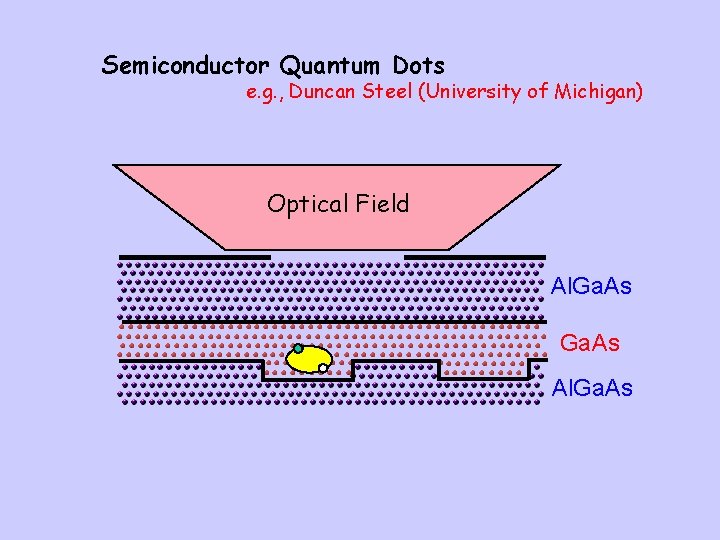
Semiconductor Quantum Dots e. g. , Duncan Steel (University of Michigan) Optical Field Al. Ga. As

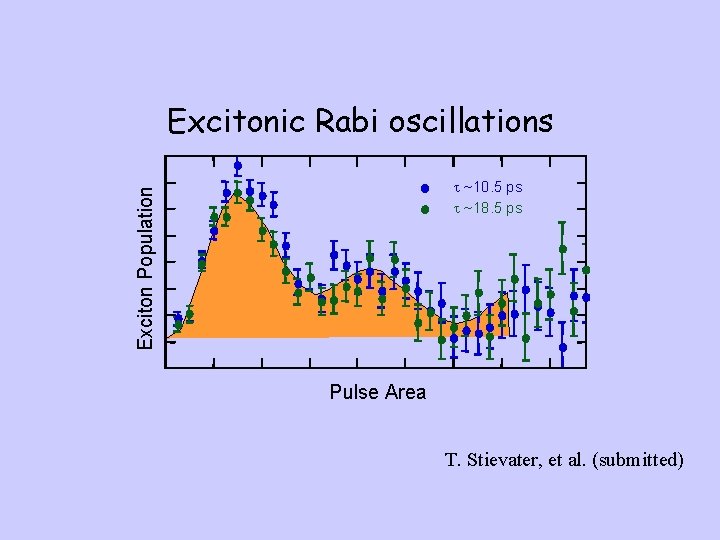
Excitonic Rabi oscillations Exciton Population t ~10. 5 ps t ~18. 5 ps Pulse Area T. Stievater, et al. (submitted)

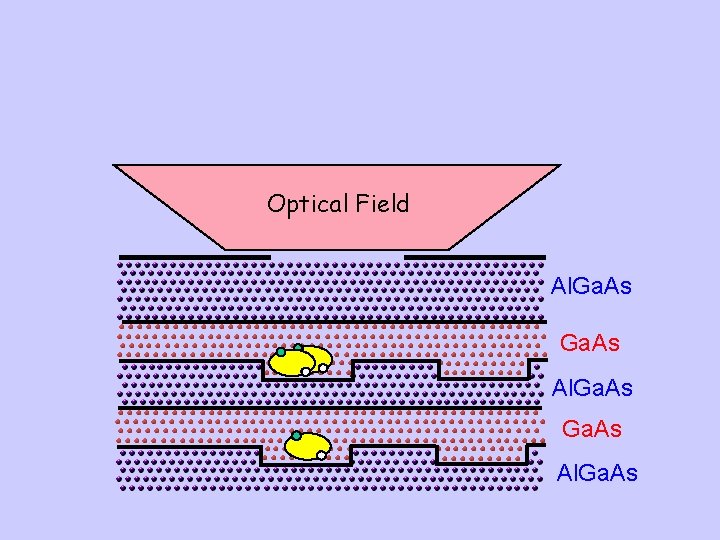
Optical Field Al. Ga. As Al. Ga. As


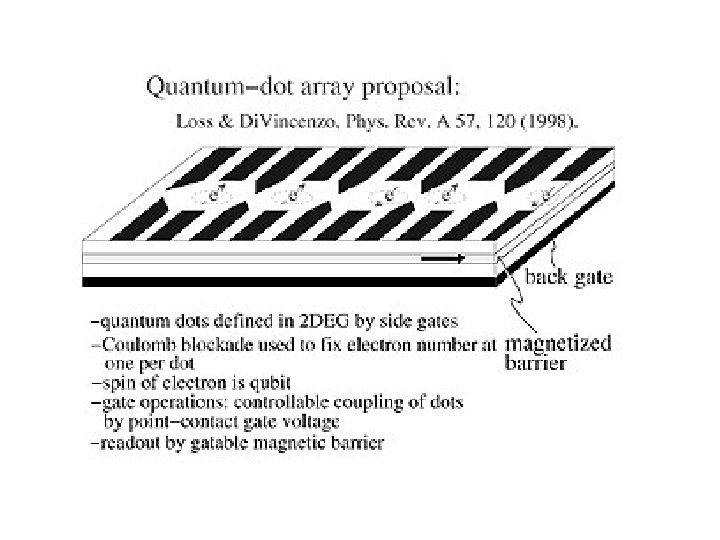
Physical Implementations 1. Individual atoms and photons a. ion traps b. atoms in optical lattices c. photon downconversion and cavity-QED 2. Superconductors a. Cooper-pair boxes (charge qubits) b. rf-SQUIDS (flux qubits) 3. Semiconductors quantum dots 4. Other condensed-matter a. NMR b. electrons floating on liquid helium c. single phosphorus atoms in silicon

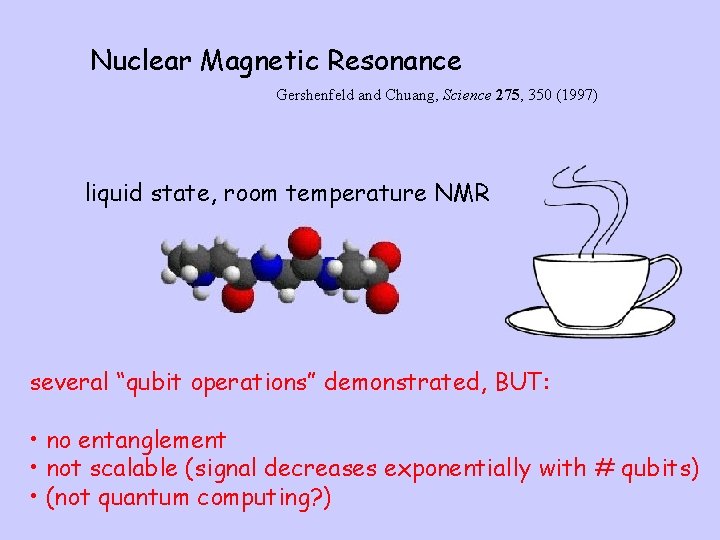
Nuclear Magnetic Resonance Gershenfeld and Chuang, Science 275, 350 (1997) liquid state, room temperature NMR several “qubit operations” demonstrated, BUT: • no entanglement • not scalable (signal decreases exponentially with # qubits) • (not quantum computing? )

Physical Implementations 1. Individual atoms and photons a. ion traps b. atoms in optical lattices c. photon downconversion and cavity-QED 2. Superconductors a. Cooper-pair boxes (charge qubits) b. rf-SQUIDS (flux qubits) 3. Semiconductors quantum dots 4. Other condensed-matter a. NMR b. electrons floating on liquid helium c. single phosphorus atoms in silicon

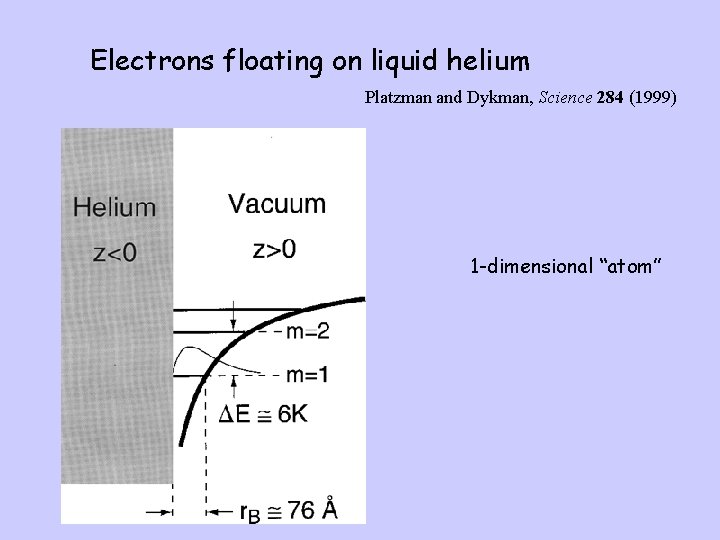
Electrons floating on liquid helium Platzman and Dykman, Science 284 (1999) 1 -dimensional “atom”

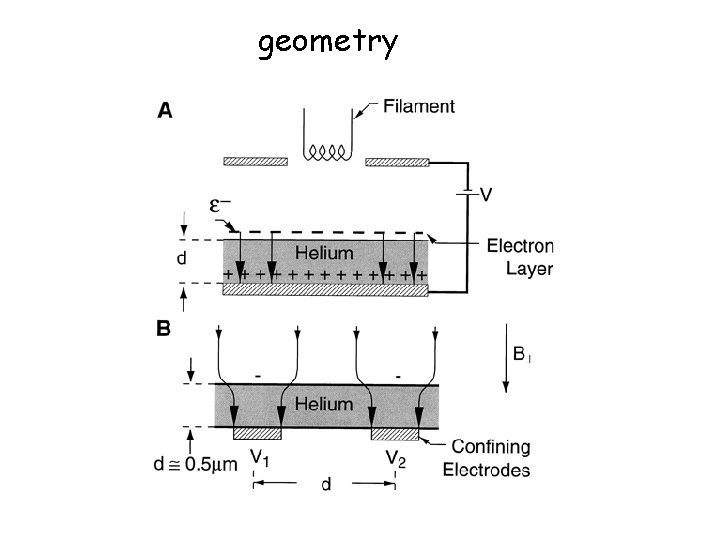
geometry

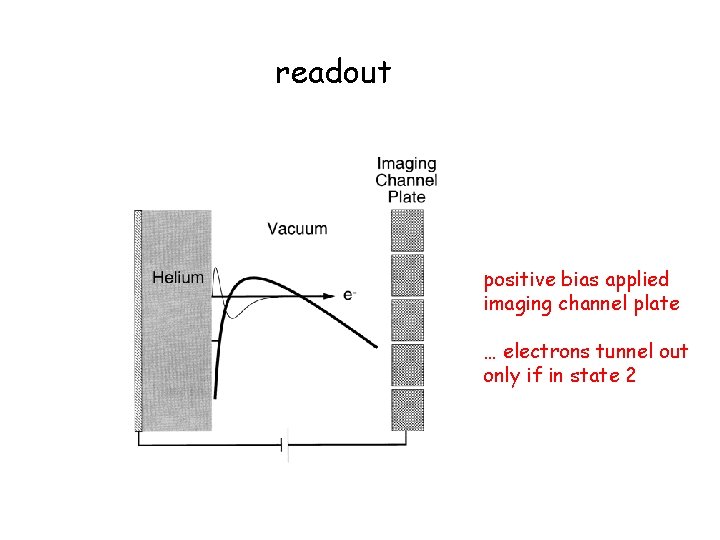
readout positive bias applied imaging channel plate … electrons tunnel out only if in state 2

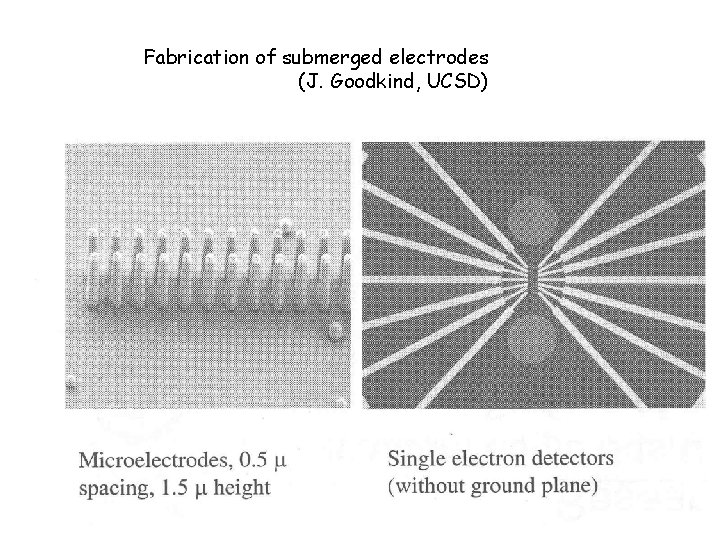
Fabrication of submerged electrodes (J. Goodkind, UCSD)

Physical Implementations 1. Individual atoms and photons a. ion traps b. atoms in optical lattices c. photon downconversion and cavity-QED 2. Superconductors a. Cooper-pair boxes (charge qubits) b. rf-SQUIDS (flux qubits) 3. Semiconductors quantum dots 4. Other condensed-matter a. NMR b. electrons floating on liquid helium c. single phosphorus atoms in silicon

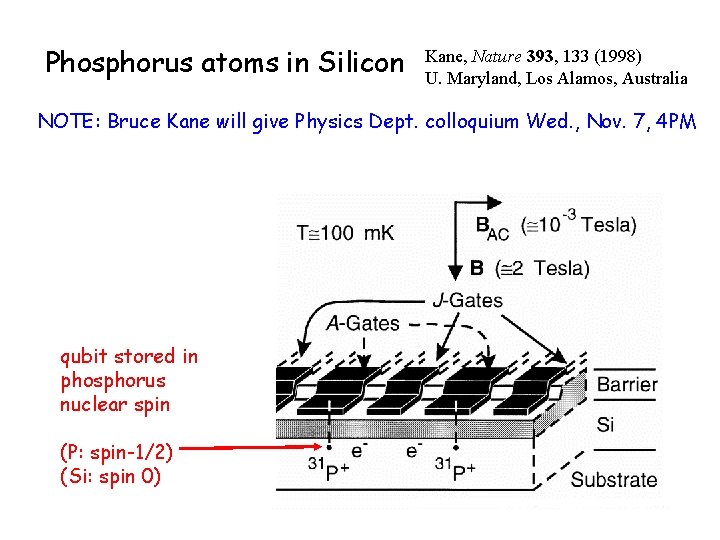
Phosphorus atoms in Silicon Kane, Nature 393, 133 (1998) U. Maryland, Los Alamos, Australia NOTE: Bruce Kane will give Physics Dept. colloquium Wed. , Nov. 7, 4 PM qubit stored in phosphorus nuclear spin (P: spin-1/2) (Si: spin 0)

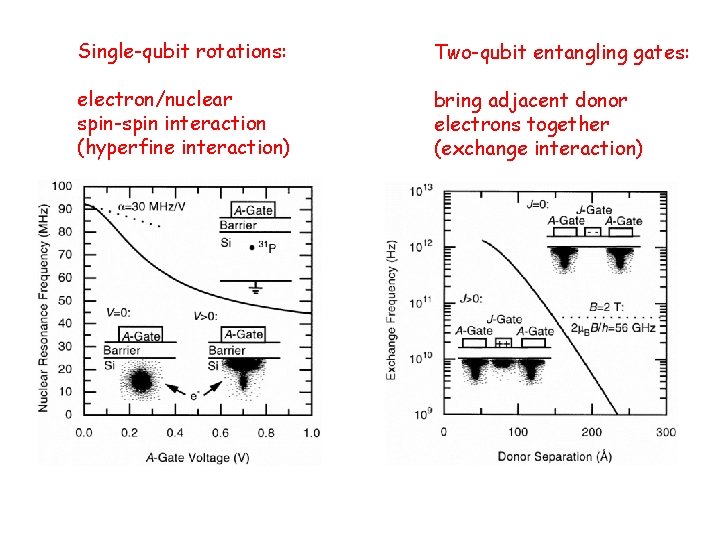
Single-qubit rotations: Two-qubit entangling gates: electron/nuclear spin-spin interaction (hyperfine interaction) bring adjacent donor electrons together (exchange interaction)

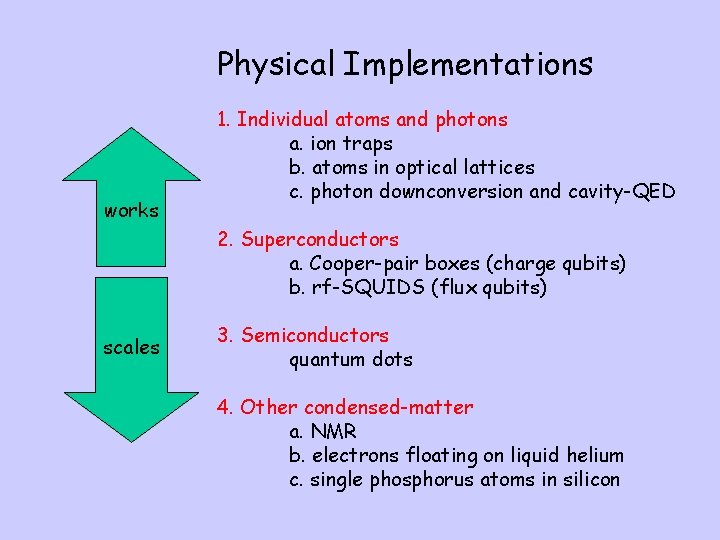
Physical Implementations works 1. Individual atoms and photons a. ion traps b. atoms in optical lattices c. photon downconversion and cavity-QED 2. Superconductors a. Cooper-pair boxes (charge qubits) b. rf-SQUIDS (flux qubits) scales 3. Semiconductors quantum dots 4. Other condensed-matter a. NMR b. electrons floating on liquid helium c. single phosphorus atoms in silicon

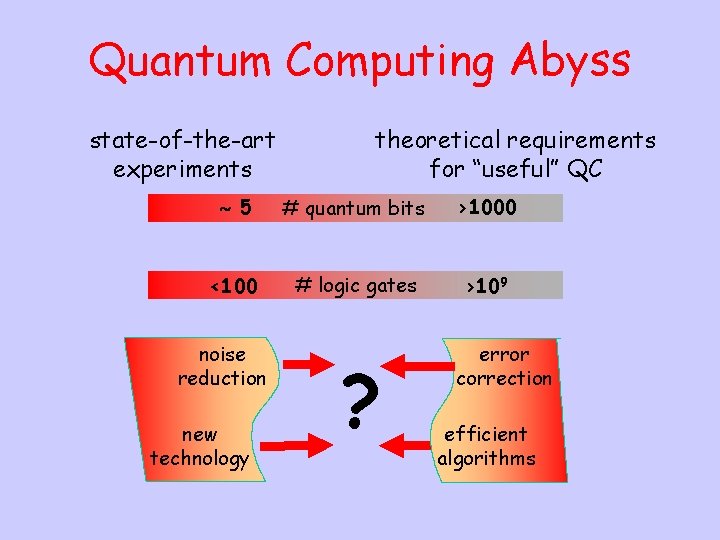
Quantum Computing Abyss state-of-the-art experiments 5 <100 noise reduction new technology theoretical requirements for “useful” QC # quantum bits # logic gates ? >1000 >109 error correction efficient algorithms
