Quantum Computer Architecture Prof Eric Rotenberg ECE 792

Quantum Computer Architecture Prof. Eric Rotenberg ECE 792 (046) Fall 2019 Topic 2: Hybrid Classical/Quantum Solvers Part A: Variational Quantum Eigensolvers

Background: eigenvectors and eigenvalues • A vector v is an eigenvector with respect to a transform (matrix) A, if multiplying A and v is the same as scaling v by a scalar value λ, which is the eigenvalue corresponding to the eigenvector v. matrix eigenvector eigenvalue for this eigenvector https: //en. wikipedia. org/wiki/Eigenvalues_and_eigenvectors ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 2

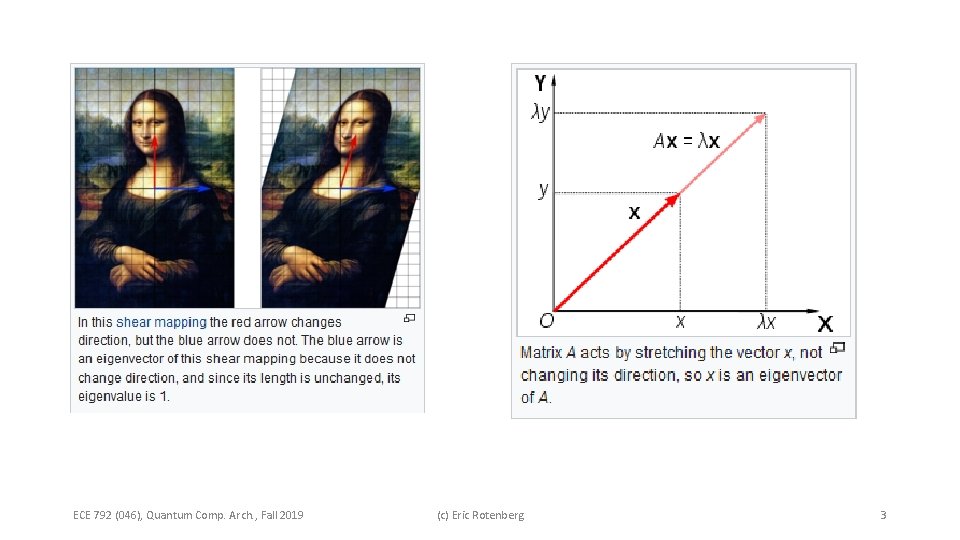
ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 3

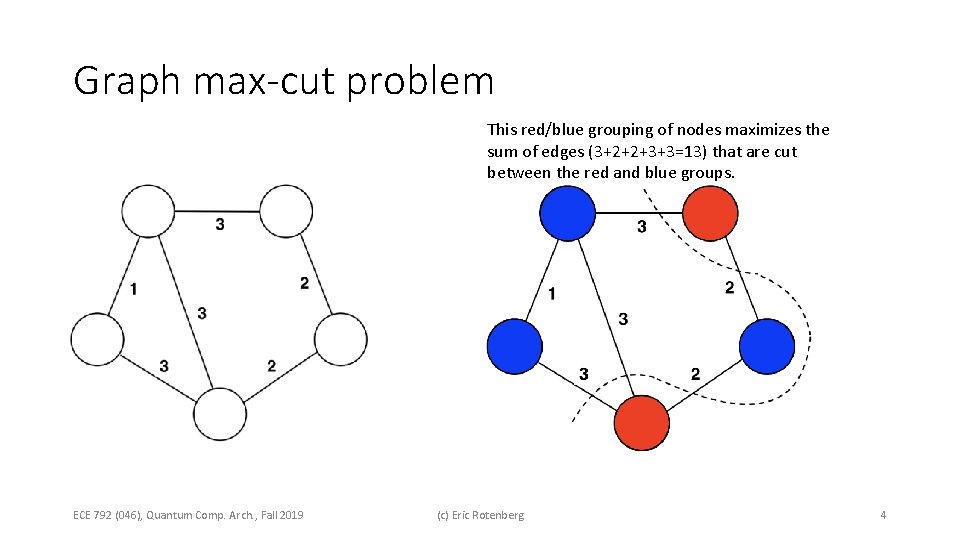
Graph max-cut problem This red/blue grouping of nodes maximizes the sum of edges (3+2+2+3+3=13) that are cut between the red and blue groups. ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 4

Analogy between max-cut and lowest-energy state (ground state) in physics ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 5

Energy states • ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 6

Energy states (cont. ) ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 7

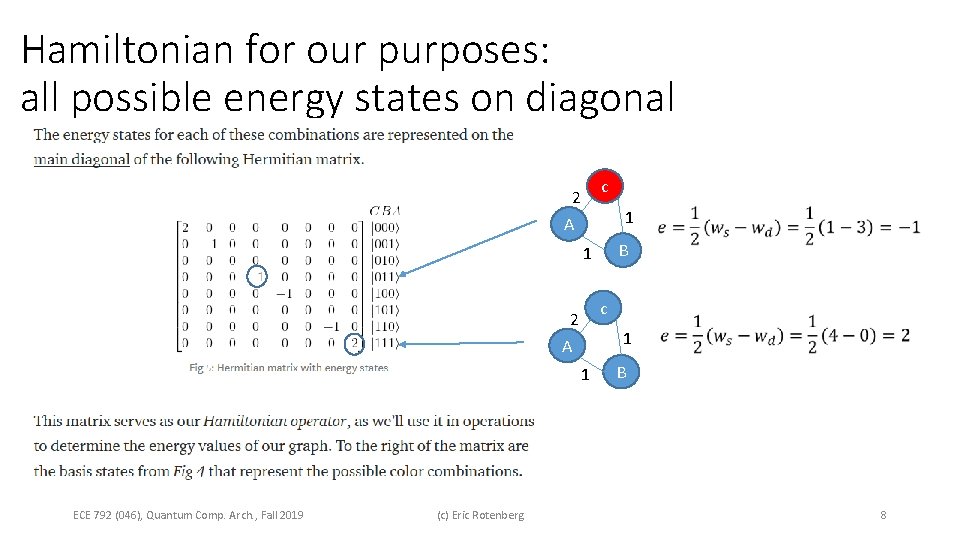
Hamiltonian for our purposes: all possible energy states on diagonal c 2 A 1 B 1 c 2 A 1 ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 1 B 8

Eigenvectors = basis states Eigenvalues = diagonal elements of Hamiltonian λ=-1 A ∙ v = λv ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 9

Expectation value • ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 10

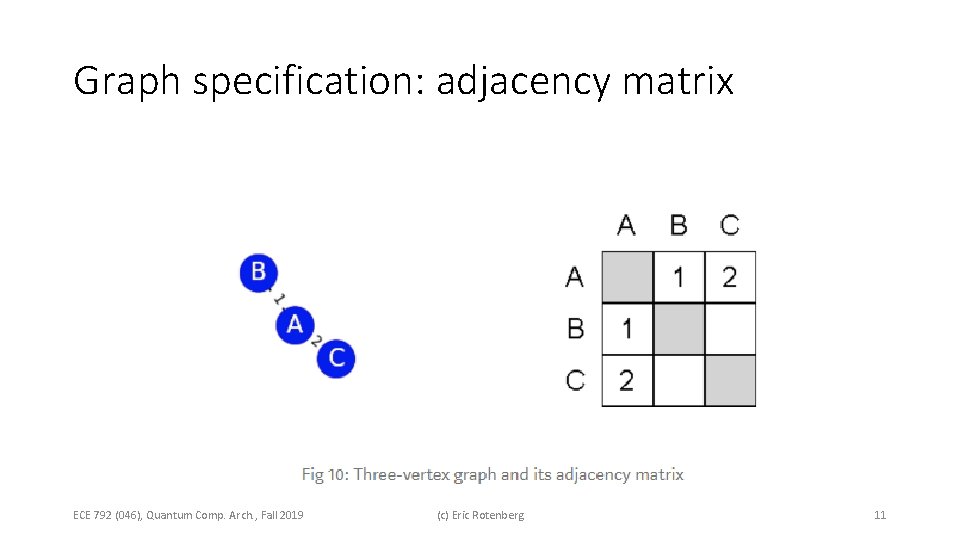
Graph specification: adjacency matrix ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 11

Computing Hamiltonian from adjacency matrix First: just AB edge ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg times 1 implied 12

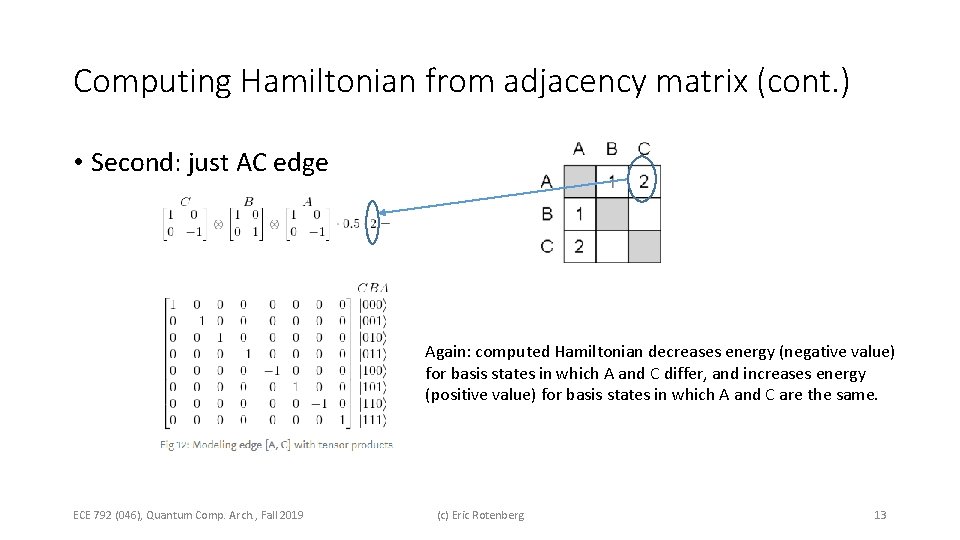
Computing Hamiltonian from adjacency matrix (cont. ) • Second: just AC edge Again: computed Hamiltonian decreases energy (negative value) for basis states in which A and C differ, and increases energy (positive value) for basis states in which A and C are the same. ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 13

Computing Hamiltonian from adjacency matrix (cont. ) And finally: take AB and AC edges together by summing the two sub-Hamiltonians = + ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 14

Computing Hamiltonian from adjacency matrix (cont. ) ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 15

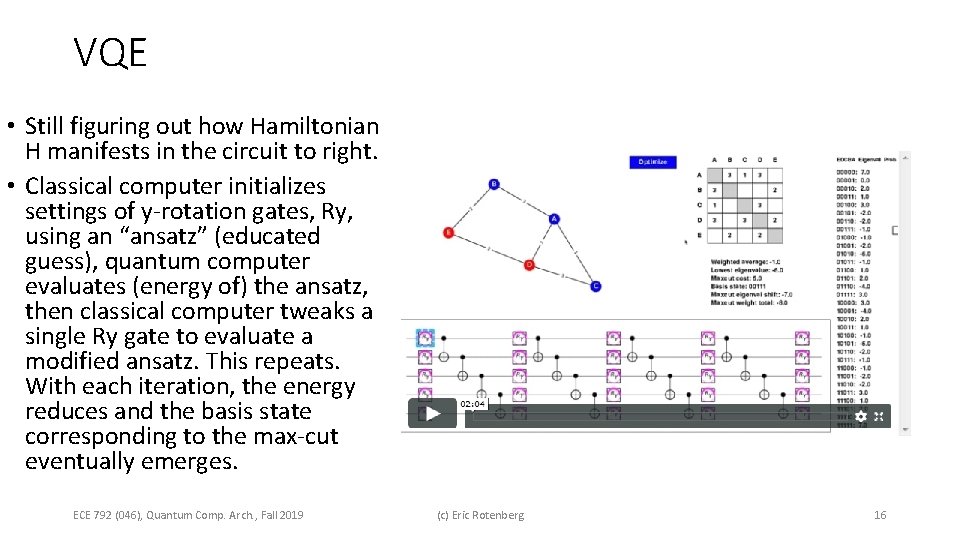
VQE • Still figuring out how Hamiltonian H manifests in the circuit to right. • Classical computer initializes settings of y-rotation gates, Ry, using an “ansatz” (educated guess), quantum computer evaluates (energy of) the ansatz, then classical computer tweaks a single Ry gate to evaluate a modified ansatz. This repeats. With each iteration, the energy reduces and the basis state corresponding to the max-cut eventually emerges. ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 16

Aside: math leading us to rotation gates • https: //en. wikipedia. org/wiki/Normal_matrix https: //en. wikipedia. org/wiki/Unitary_matrix https: //en. wikipedia. org/wiki/Hermitian_matrix ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 17

Aside: math leading us to rotation gates (cont. ) • ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 18

Aside: math leading us to rotation gates (cont. ) • Finding the eigenvalues of A: https: //en. wikipedia. org/wiki/Eigenvalues_and_eigenvectors • Determinant of a 2 x 2 matrix: https: //en. wikipedia. org/wiki/Determinant ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 19

Aside: math leading us to rotation gates (cont. ) • Exercise 2. 11, p. 69: “(Eigendecomposition of the Pauli matrices) Find the eigenvectors, eigenvalues, and diagonal representations of the Pauli matrices X, Y, and Z. ” characteristic equation eigenvectors eigenvalues ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 20

Aside: math leading us to rotation gates (cont. ) • Exercise 2. 11, p. 69: “(Eigendecomposition of the Pauli matrices) Find the eigenvectors, eigenvalues, and diagonal representations of the Pauli matrices X, Y, and Z. ” characteristic equation eigenvectors eigenvalues ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 21

Aside: math leading us to rotation gates (cont. ) • Exercise 2. 11, p. 69: “(Eigendecomposition of the Pauli matrices) Find the eigenvectors, eigenvalues, and diagonal representations of the Pauli matrices X, Y, and Z. ” characteristic equation eigenvectors eigenvalues ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 22

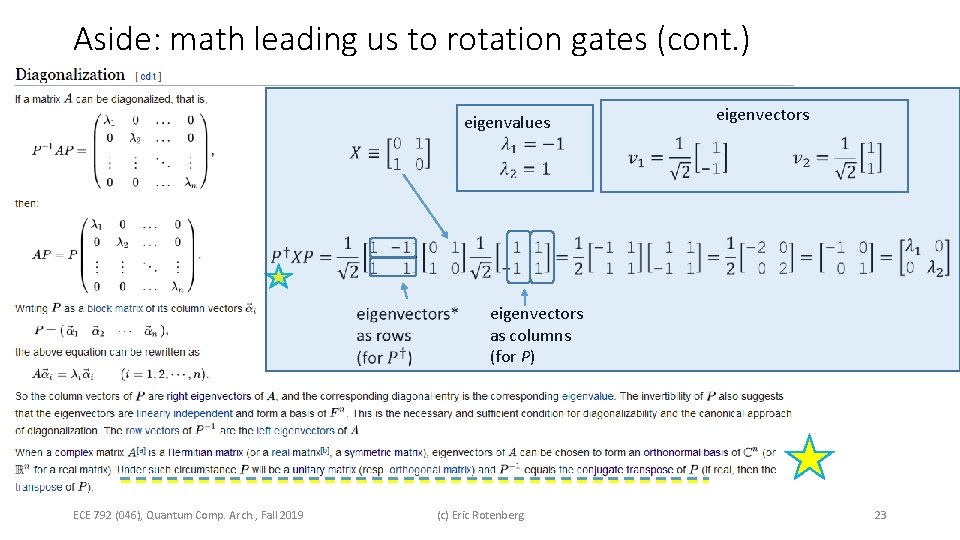
Aside: math leading us to rotation gates (cont. ) eigenvalues eigenvectors ECE 792 (046), Quantum Comp. Arch. , Fall 2019 eigenvectors as columns (for P) (c) Eric Rotenberg 23

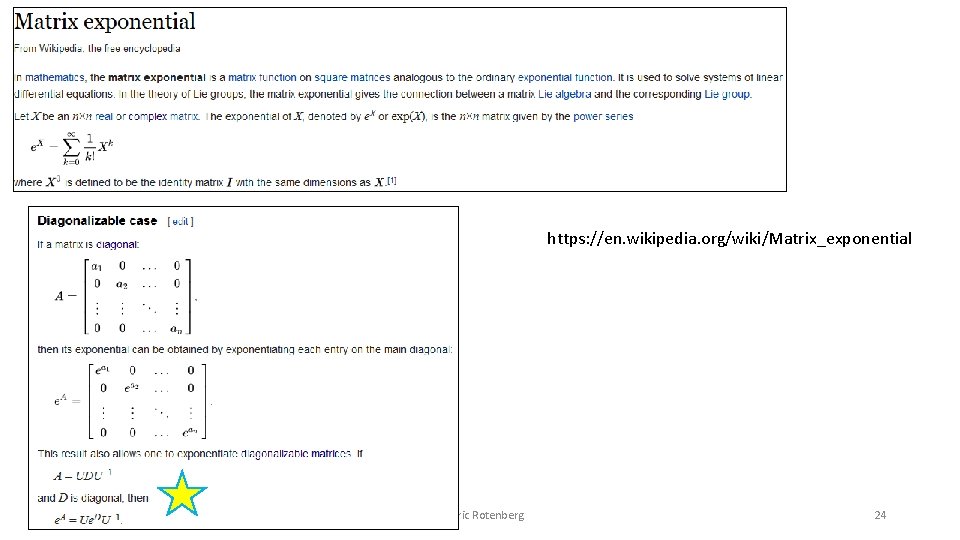
https: //en. wikipedia. org/wiki/Matrix_exponential ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 24

Rotation gates: exponentiated Pauli gates • ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 25

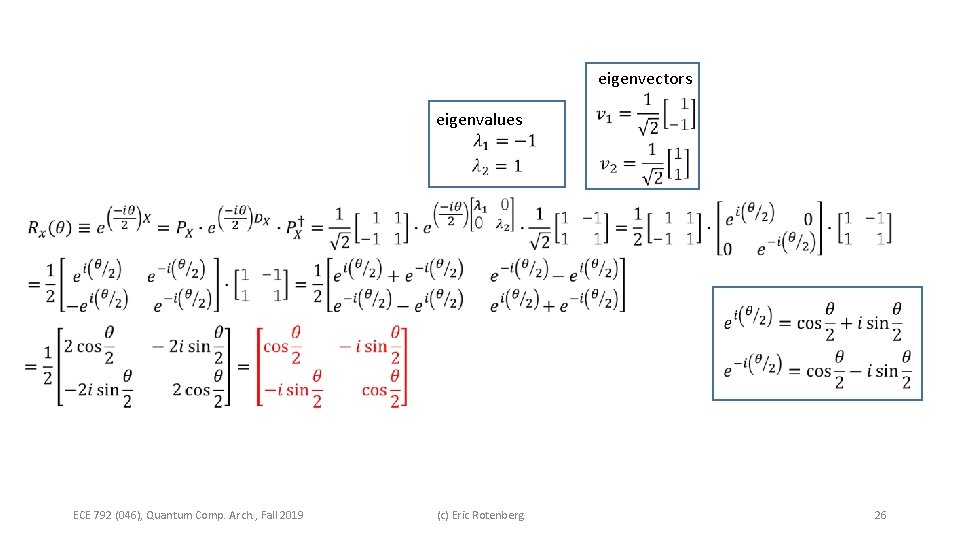
eigenvectors eigenvalues ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 26

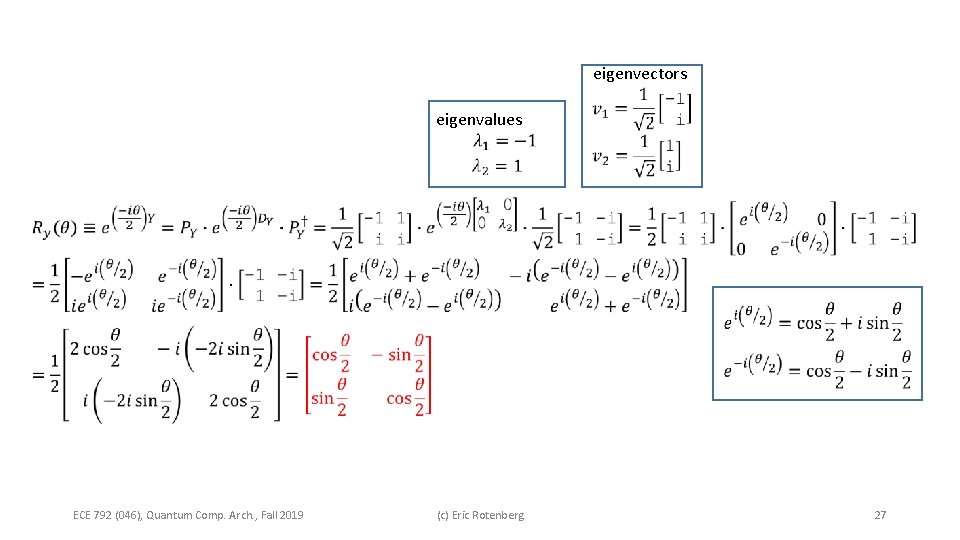
eigenvectors eigenvalues ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 27

eigenvectors eigenvalues ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 28

Identity from textbook ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 29

Revisit spectral decomposition • ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 30

Revisit spectral decomposition (cont. ) eigenvectors eigenvalues ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 31

Summing up derivation of rotation gates • Three alternate techniques that achieve the same thing (for Hermitian-and-unitary matrix) • Exploit diagonalization • Exploit spectral decomposition • Exploit this identity: ECE 792 (046), Quantum Comp. Arch. , Fall 2019 eigenvector column matrix diagonal eigenvalue matrix eigenvector row matrix (c) Eric Rotenberg 32

Understanding VQE circuits based on rotation gates (1) • https: //en. wikipedia. org/wiki/Lie_product_formula X ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 33

Understanding VQE circuits based on rotation gates (2 a) https: //vtomole. com/blog/2019/04/07/trotter • ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 34

Understanding VQE circuits based on rotation gates (2 b) https: //vtomole. com/blog/2019/04/07/trotter • ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 35

Understanding VQE circuits based on rotation gates (3) • ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 36

ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 37

Backup slides ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 38

ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 39