Quantum Computer Architecture Prof Eric Rotenberg ECE 792

Quantum Computer Architecture Prof. Eric Rotenberg ECE 792 (046) Fall 2019 Topic 1: Quantum Circuits Part C: Circuit Analysis

Outline • Unitary matrix • • • Identity matrix Inverse matrix Conjugate transpose matrix Definition of unitary matrix Significance of unitary matrices in quantum circuits • Kronecker Product • Circuit analysis • Use Kronecker product to combine unitary matrices at each step • Use matrix multiplication across all steps for circuit’s overall unitary matrix ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 2

Identity Matrix • In is the nxn identity matrix. Examples: • If A is an nxn square matrix: • Example: ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 3

Inverse of a Square Matrix https: //en. wikipedia. org/wiki/Invertible_matrix …if A-1 exists (A is invertible). ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 4

https: //en. wikipedia. org/wiki/Conjugate_transpose Conjugate Transpose Matrix • “…the conjugate transpose or Hermitian transpose of an m-by-n matrix A with complex entries is the n-by-m matrix AH obtained from A by taking the transpose and then taking the complex conjugate of each entry. (The complex conjugate of a+ib, where a and b are real numbers, is a−ib. )” ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 5

https: //en. wikipedia. org/wiki/Conjugate_transpose Conjugate Transpose Matrix (cont. ) ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 6

https: //en. wikipedia. org/wiki/Unitary_matrix Unitary Matrix • ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 7

Significance of Unitary Matrices • Elementary quantum gates are unitary matrices. • Any unitary matrix can be implemented by combining a set of universal elementary quantum gates. • Any logic function that can be expressed as a unitary matrix, can be synthesized to a quantum circuit. ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 8

https: //en. wikipedia. org/wiki/Kronecker_product Kronecker product “In mathematics, the Kronecker product, denoted by ⊗, is an operation on two matrices of arbitrary size resulting in a block matrix. It is a generalization of the outer product (which is denoted by the same symbol) from vectors to matrices, and gives the matrix of the tensor product with respect to a standard choice of basis. The Kronecker product should not be confused with the usual matrix multiplication, which is an entirely different operation. ” Note: Kronecker product is a special case of tensor product (both denoted by ⊗). So people often use the terms interchangeably when analyzing quantum circuits. ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 9

Kronecker product (cont. ) https: //en. wikipedia. org/wiki/Kronecker_product Replicate B mxn times. Each replica is scaled by a single element of A. ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 10

Kronecker product (cont. ) ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg https: //en. wikipedia. org/wiki/Kronecker_product 11

Significance of Kronecker Product • Informally, you can think of it as a way to combine smaller vector spaces (fewer dimensions) into larger vector spaces (more dimensions). • It facilitates combining the smaller unitary matrices of elementary quantum gates at a given time step, each of which operate on a subset of qubits, to derive the larger unitary matrix that operates on all the qubits as a whole. That is, it facilitates combining multiple local unitary matrices into a single global unitary matrix. ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 12

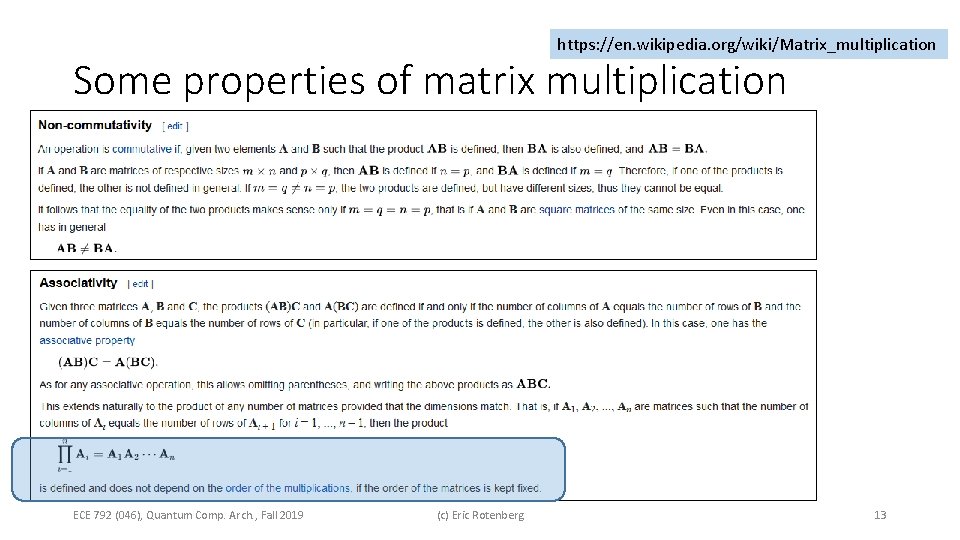
https: //en. wikipedia. org/wiki/Matrix_multiplication Some properties of matrix multiplication ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 13

Circuit Analysis • Circuit analysis, in this context, means calculating the overall unitary matrix of an entire quantum circuit. • Two tools: Kronecker product at each time step and matrix multiplication across timesteps. 1. Use the Kronecker product at each time step to calculate the global (applies to all qubits) unitary matrix at that timestep. 2. Starting with the global unitary matrix at the last time step, and working backwards to the first time step, multiply all the unitary matrices together. U 1 U 2 ECE 792 (046), Quantum Comp. Arch. , Fall 2019 U 3 (c) Eric Rotenberg Matrix multiplication is associative. In general, it is not commutative. 14

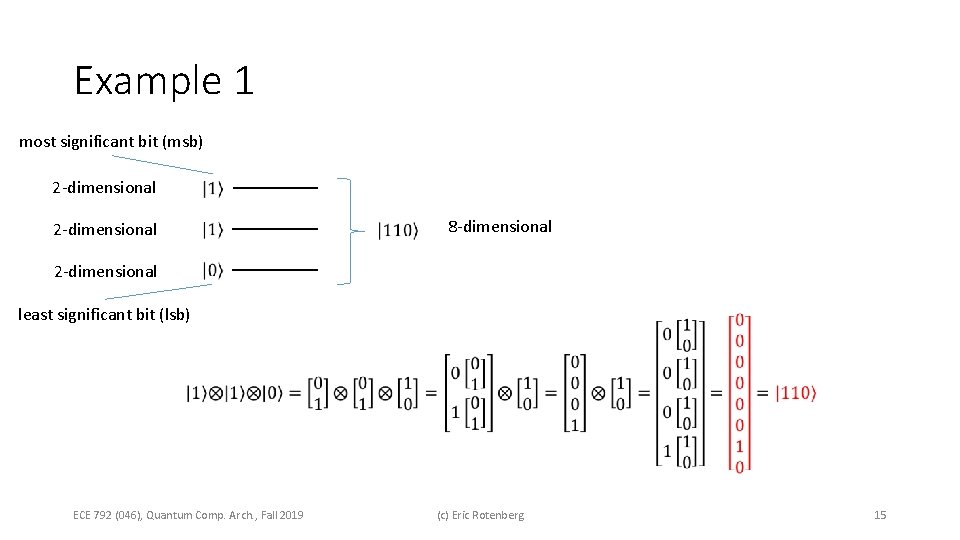
Example 1 most significant bit (msb) 2 -dimensional 8 -dimensional least significant bit (lsb) ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 15

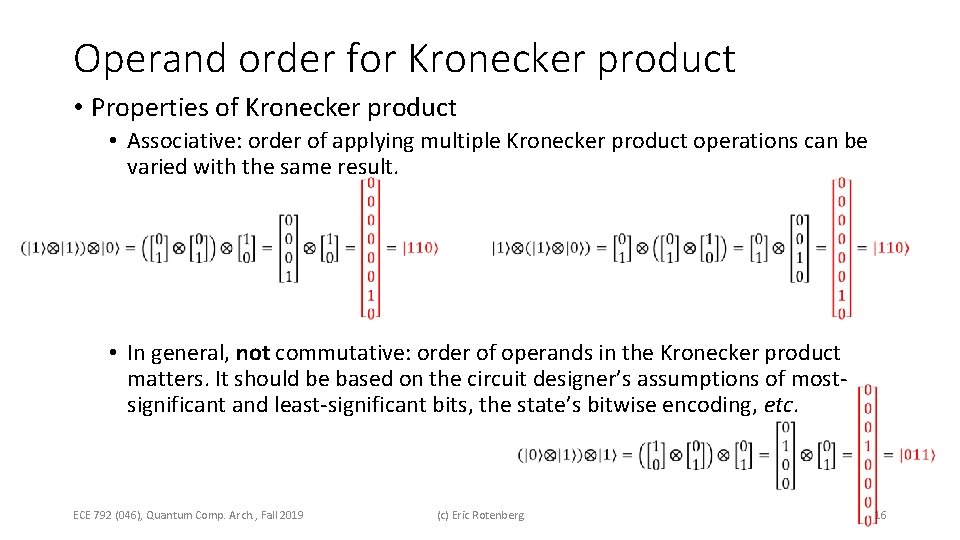
Operand order for Kronecker product • Properties of Kronecker product • Associative: order of applying multiple Kronecker product operations can be varied with the same result. • In general, not commutative: order of operands in the Kronecker product matters. It should be based on the circuit designer’s assumptions of most significant and least-significant bits, the state’s bitwise encoding, etc. ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 16

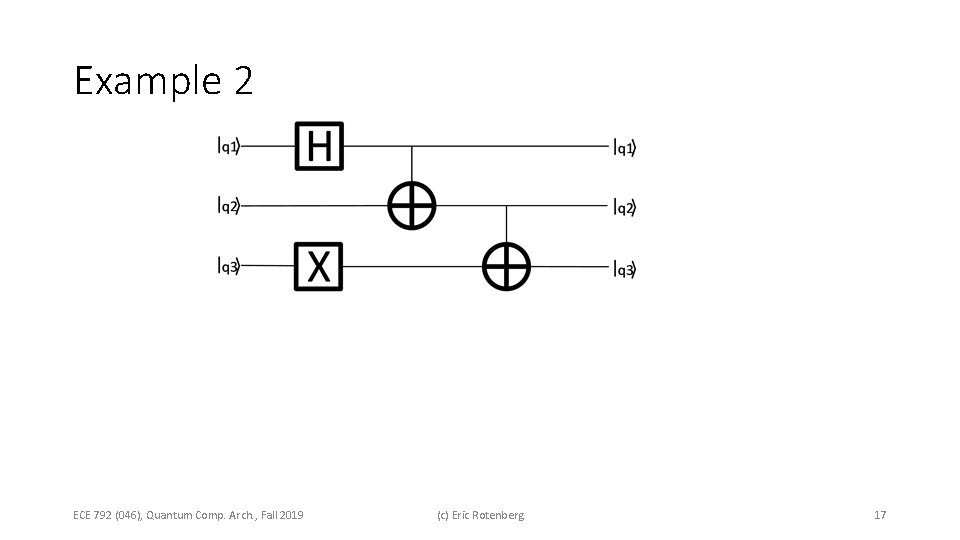
Example 2 ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 17

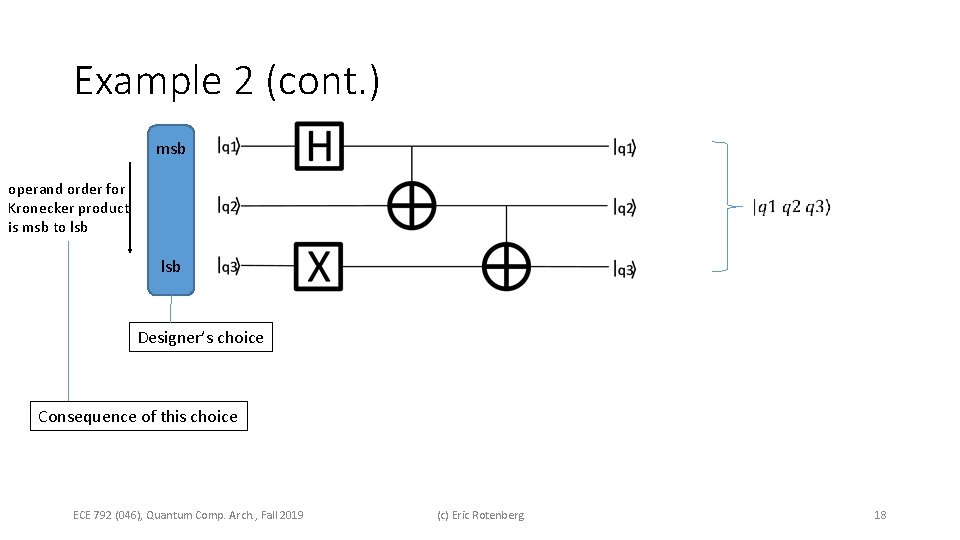
Example 2 (cont. ) msb operand order for Kronecker product is msb to lsb Designer’s choice Consequence of this choice ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 18

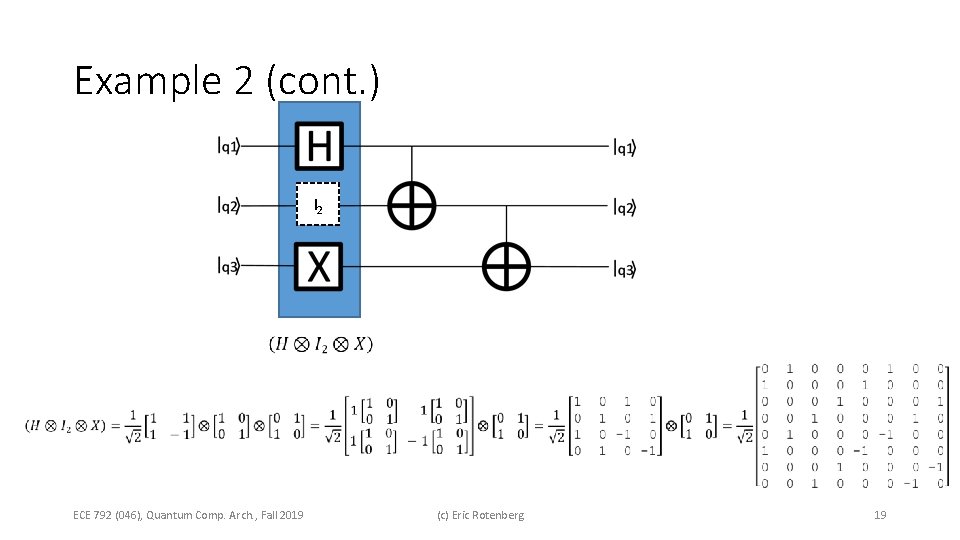
Example 2 (cont. ) I 2 ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 19

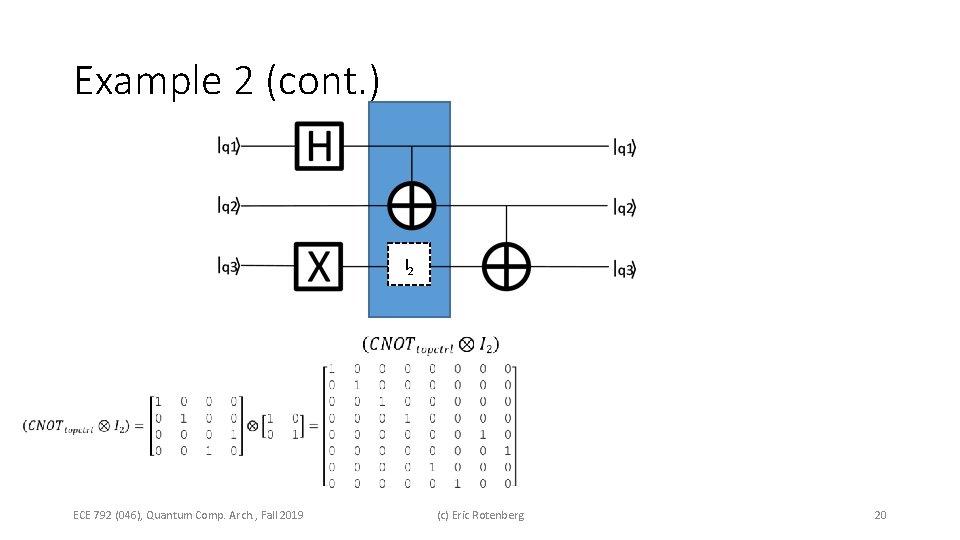
Example 2 (cont. ) I 2 ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 20

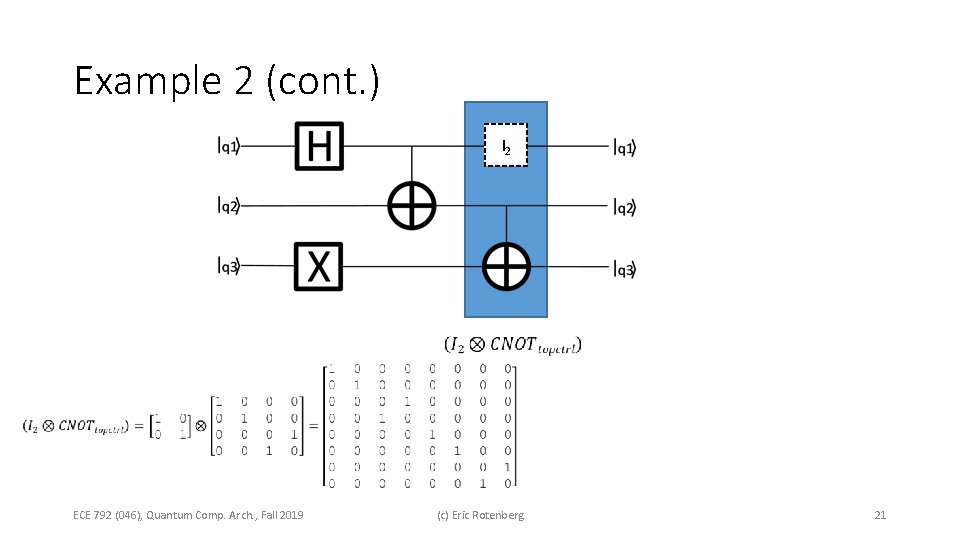
Example 2 (cont. ) I 2 ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 21

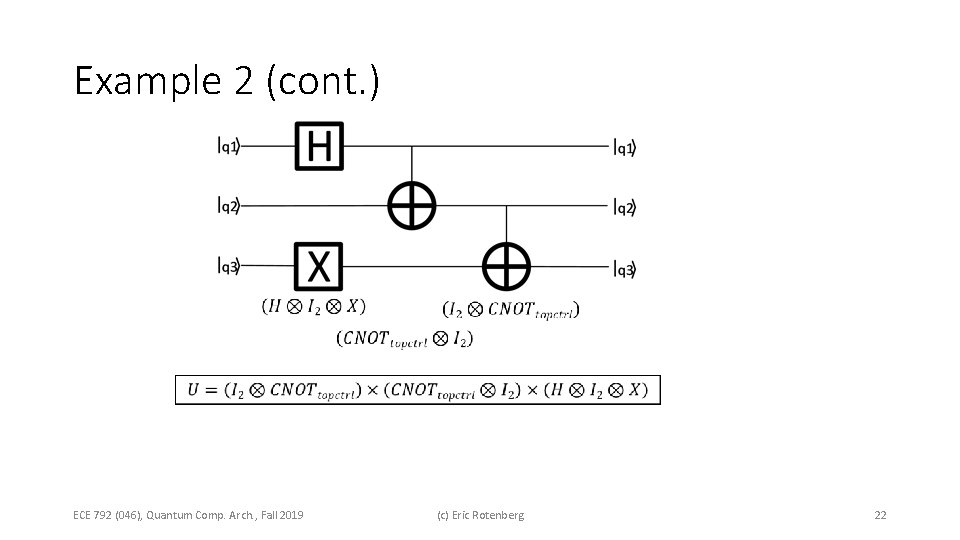
Example 2 (cont. ) ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 22

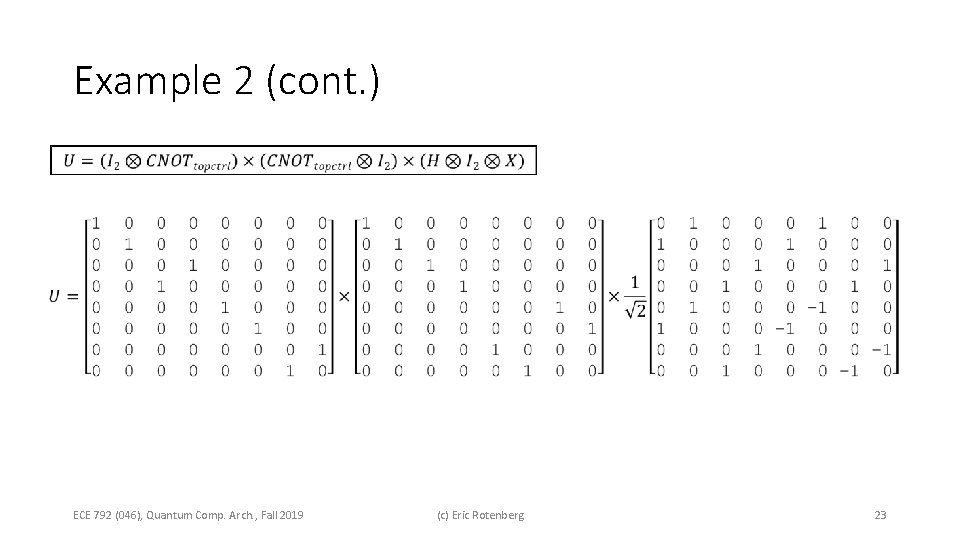
Example 2 (cont. ) ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 23

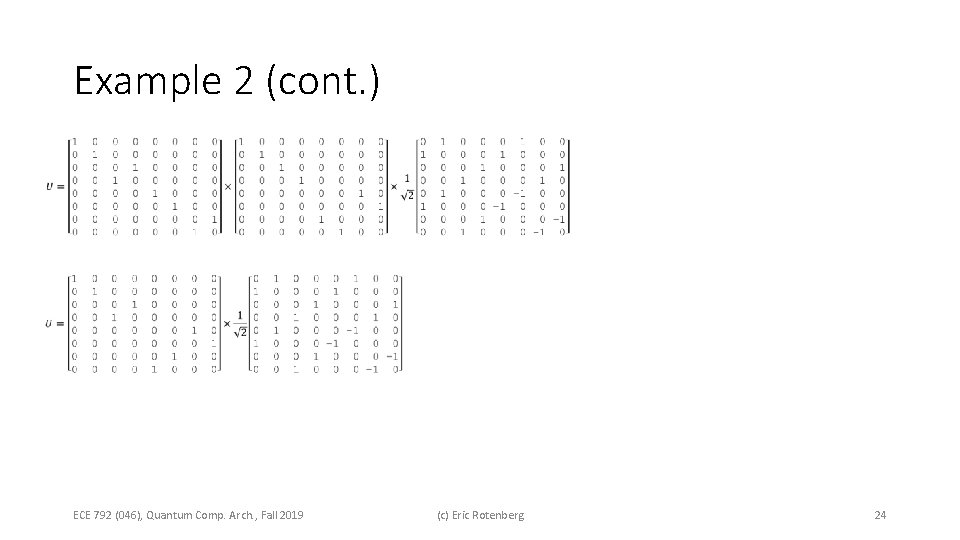
Example 2 (cont. ) ECE 792 (046), Quantum Comp. Arch. , Fall 2019 (c) Eric Rotenberg 24