Quantum Computation with coupled quantum dots 1 Two

Quantum Computation with coupled quantum dots 1

• • Two sides of a coin Two different polarization of a photon Alignment of a nuclear spin in a uniform magnetic field Two states of an electron orbiting a single atom. . . 2

Qubit Manipulation Gate form = qubit CNOT + single qubit gates a operation universal Set. Single qubit gate: Hadamard gate H Pauli gates X, Y and Z … Quantum Algorithm is a (2^N)x(2^N) unitary Two qubit gate: Swap gate Controlled-Not gate or CNOT, … 3

Physical systems actively considered for quantum computer implementation • Liquid-state NMR • NMR spin lattices • Linear ion-trap spectroscopy • Neutral-atom optical lattices • Cavity QED + atoms • Linear optics with single photons • Nitrogen vacancies in diamond • Topologically ordered materials • Electrons on liquid He • Small Josephson junctions – “charge” qubits – “flux” qubits • Spin spectroscopies, impurities in semiconductors • Coupled quantum dots – Qubits: spin, charge, excitons – Exchange coupled, cavity coupled 4

Di. Vincenzo Criteria A qubit must be ‘well characterized’ in the sense that one has a • Atheoretical scalabledescription physicalnotsystem with well good only of the qubit itself (in terms of ancharactrized internal Hamiltonian, accurate knowledge of all physical qubits parameters, etc. ), but also of all relevant mechanisms that couple • The ability toeach initialize the state of the qubits among other and to the environment. qubits to a simple fixed state • Long relevant decoherence times, role: much The word ‘scalable’ plays an important A proposal a quantum computer must at least longerfor than the gate operation timein principle be preparable or manufacturable in large numbers of qubits, • A ifuniversal set of quantum even current fundamental experimentsgates. are performed with Only few qubits. • A qubit-specific measurment capability. 5

Di. Vincenzo Criteria • A scalable physical system with well charactrized qubits • The ability to initialize the state of the to aneeds simple fixed state everyqubits computation to be started in an initially known state such as |000. . . 0>. Having also a fast initialization mechanism at • Longhand relevant decoherence times, much is crucial for quantum error correction longer than the gate operation time • A universal set of quantum gates. • A qubit-specific measurment capability. 6

Di. Vincenzo Criteria Quantum states in contact with the outside world ultimately evolve A scalable physical system with well into • a fully mixed states. By encoding information not directly into single charactrized qubits, but rather qubits into ‘logical qubits’ consisting of several single qubits, a certain amount of errors due to decoherence and • The ability initialize the state of the imperfect gates maybetocorrected, depending on what kind of code qubits a simple is used. There istohowever still afixed limit onstate how faulty elementary gates are allowed to be: The accuracy threshold theorem states that error • Long relevant decoherence correction is possible if the error probabilitytimes, per gatemuch is smaller than longer than gate value operation A certain threshold. Thethe threshold dependstime on the error models Studied and on the details of the codes considered. Typical values are • A universal set of quantum gates. in the range of to 10^(-5) to 10^(-3) , implying that decoherence times be a thousand to ameasurment hundred thousand times longer • must A qubit-specific capability. than gate operation times. 7

Di. Vincenzo Criteria • A scalable physical system with well charactrized qubits The quantum is possible in the model • generic The ability tocomputing initialize the state ofstandard the if certain one- to andatwo-qubit available. The single qubits simple gates fixedarestate gates may be either implemented directly, or can be approximated arbitrary precision using a finite settimes, of gates. The only • to Long relevant decoherence much necessary two-qubit gate operation is the controlled-not longer than the gate time gate. • A universal set of quantum gates. • A qubit-specific measurment capability. 8

Di. Vincenzo Criteria • A scalable physical system with well Measuringcharactrized qubits without disturbing qubits the rest of the quantum computer is required in the verification steps of quantum error correction and, not remarkably, in order to reveal the outcome a computation. • The ability to initialize theofstate of the A meas-urement qubits is said toto have 100% quantum if it yields, performed a simple fixed efficiency state on a state the outcome “ 0” with probability p and relevant “ 1” with probability (1 − p) independent of α, the states of • Long decoherence times, much neighboring qubits, than or anythe othergate parameters of the system. longer operation time Real measure-ments cannot have perfect quantum efficiency. • A universal set of quantum gates. • A qubit-specific measurment capability. 9

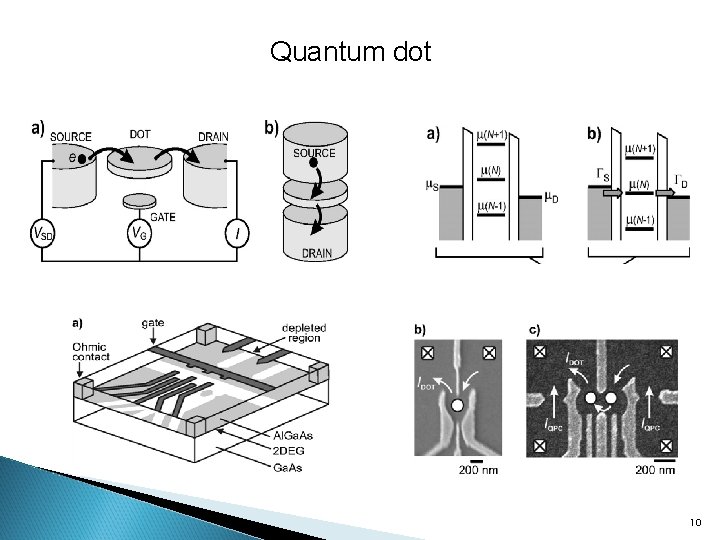
Quantum dot 10

QC with quantum dots the physical system representing a qubit is given by the localized spin state of one electron, and the computational basis states and are identified with the two spin states and , respectively. 11

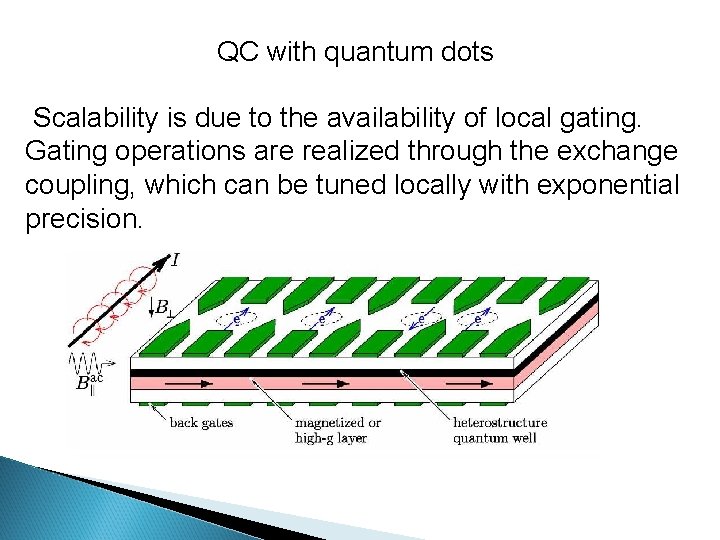
QC with quantum dots Scalability is due to the availability of local gating. Gating operations are realized through the exchange coupling, which can be tuned locally with exponential precision.

QC with quantum dots In spin qubits, initialization could be achieved by either forcing the spins to align with a strong externally applied magnetic field, or by performing a measurement on the dot followed by a subsequent rotation of the state depending on the measurement outcome. 13

QC with quantum dots Initialization of the quantum computer could be realized at low temperature T by applying an Experiments are usually performed in dilution Refrigerators with base external magnetic field B satisfying |gμB| ≫ k. T , temperature around 20 m. K, which is smaller than typical Zeeman where g is them. K g-factor, is using Bohr’s magneton, and k splittings (∼ 300 at B = 1 Tμand the bulk value g = − 0. 44). initialization time is constant. of the order of. After a few relaxation times, which in is. The the Boltzmann a sufficiently long Ga. As dots have been reported to be as high as ∼ 1 s. time, virtually all spins will have equilibrated to their thermodynamic ground state |0> = |↑>.

QC with quantum dots In quantum dots where electron spins are used as qubits, the most important mechanisms of decoherence are the spin-orbit and the hyperfine interaction

QC with quantum dots An electron moving through a solid experiences electric fields, from charged • Dresselhaus contribution atoms in the lattice. This electric fields lead to a net contribution to the spinorbit interaction. This effect is known as the Dresselhaus contribution to the spin-orbit interaction and its Hamiltonian for 2 DEG with strong confinement • Rashba contribution along growth direction (001) reads • Hyperfine interaction Where depends on the material properties and on

QC with quantum dots Electric fields associated with asymmetric confining potentials also give Dresselhaus contribution rise to a spin-orbit interaction (SIA, or structural inversion asymmetry). The spin-orbit contribution from SIA is known as the Rashba term. Assuming that the confining electric field is along the z axis, the Hamiltonian for 2 DEG of Rashba contribution the Rashba contribution reads Hyperfine interaction Where depends on the material specific and on the confining potential

QC with quantum dots The spin of an electron in an atom can interact with the spin of “its” atomic nucleus through the hyperfine coupling. An electron Dresselhaus contribution spin in a quantum dot, in contrast, may interact with many nuclear spins in the host material. The Hamiltonian for the Fermi Contact hyperfine interaction is then given by Rashba contribution Hyperfine interaction Where and are the spin operator for nucleus k and the electron spin Respectively

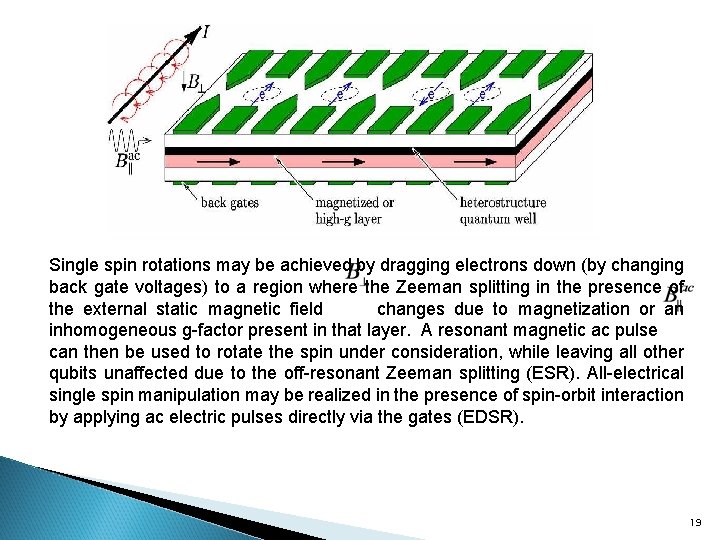
Single spin rotations may be achieved by dragging electrons down (by changing back gate voltages) to a region where the Zeeman splitting in the presence of the external static magnetic field changes due to magnetization or an inhomogeneous g-factor present in that layer. A resonant magnetic ac pulse can then be used to rotate the spin under consideration, while leaving all other qubits unaffected due to the off-resonant Zeeman splitting (ESR). All-electrical single spin manipulation may be realized in the presence of spin-orbit interaction by applying ac electric pulses directly via the gates (EDSR). 19

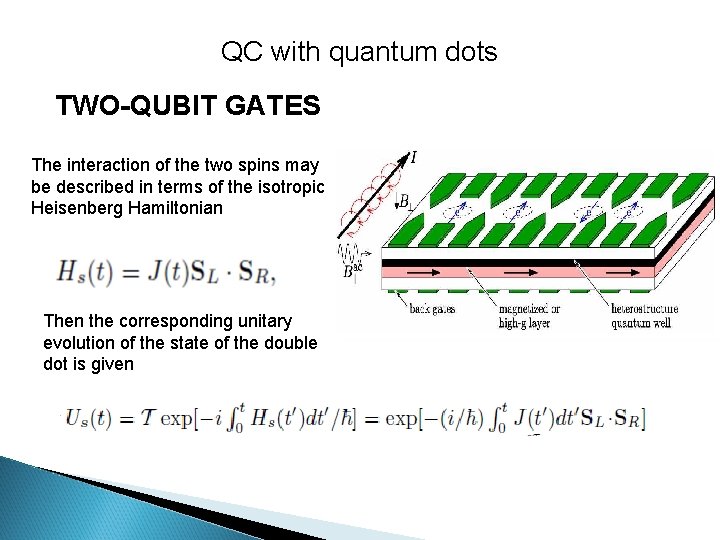
QC with quantum dots TWO-QUBIT GATES The interaction of the two spins may be described in terms of the isotropic Heisenberg Hamiltonian Then the corresponding unitary evolution of the state of the double dot is given

QC with quantum dots For the constant intraction and time s. t performs the so-called ‘square-root of swap’ denoted by This gate together with single-qubit rotations about a fixed (say, the z-) axis can be used to synthesize the cnot operation as

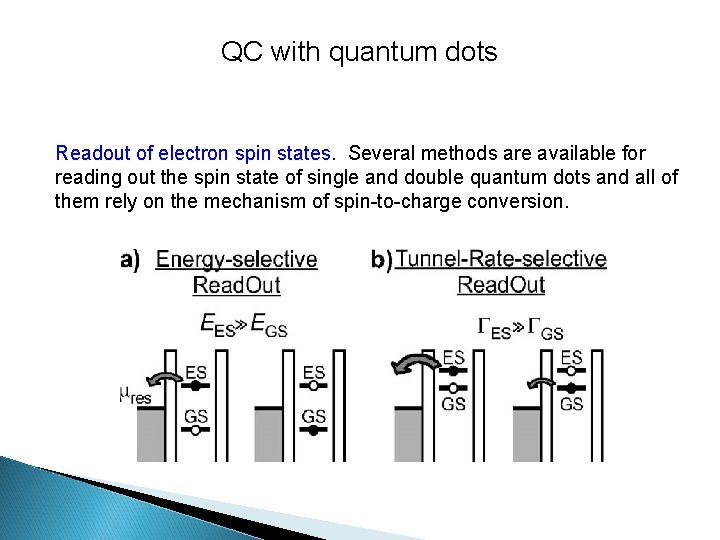
QC with quantum dots Readout of electron spin states. Several methods are available for reading out the spin state of single and double quantum dots and all of them rely on the mechanism of spin-to-charge conversion.

References: - D. Loss, D. P. Di. Vincenzo Phys. Rev. A 57, 120 -126 (1998) - R. Hanson, L. P. Kouwenhoven, J. R. Petta, S. Tarucha, L. M. K. Vandersypen, Rev. Mod. Phys, 79, 1217 (2007) 23