Quantum Computation and Quantum Information Lecture 3 Part

Quantum Computation and Quantum Information – Lecture 3 Part 1 of CS 406 – Research Directions in Computing Nick Papanikolaou

Motivation l l l Quantum computers are built from wires and logic gates, just as classical computers are The potential of such devices stems from the ability to manipulate superpositions of states Quantum algorithms solve problems which are not known to be solvable classically!

Lecture 3 Topics l l Quantum logic gates Simple quantum circuits Quantum teleportation as a circuit Deutsch’s quantum algorithm

Quantum vs. classical gates l l The simplest boolean gate is NOT, with truth table: in out 0 1 1 0 Quantum gates have to be defined not only on the equivalents of 0 and 1, but on their superpositions too!

Quantum NOT gate: Linearity l Suppose we define a quantum NOT gate as follows: l The action of the quantum NOT gate on a superposition must then be: l All quantum operations are linear

The NOT Gate as a Matrix l l Because all quantum operations have to be linear, we can represent the action of a quantum gate by a matrix The quantum NOT, or Pauli-X gate, is written:

Quantum State Vectors l l Remember that a quantum state is represented by a vector Notation:

Quantum NOT l We can express the NOT operation on a general qubit as matrix multiplication:

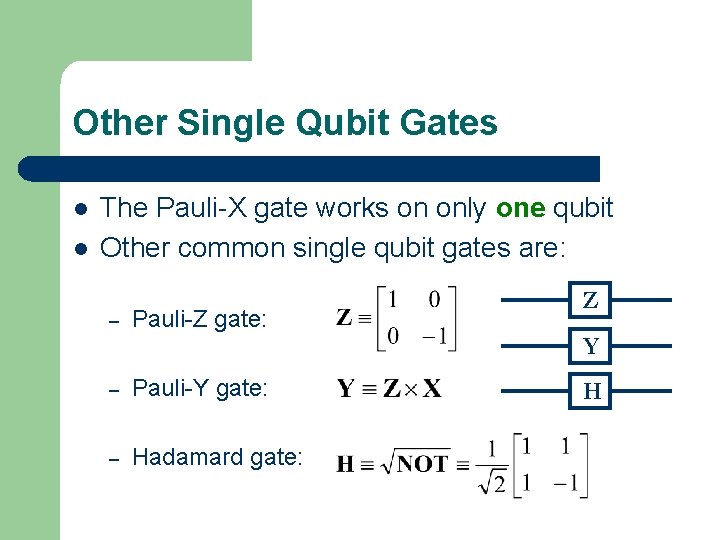
Other Single Qubit Gates l l The Pauli-X gate works on only one qubit Other common single qubit gates are: – Pauli-Z gate: – Pauli-Y gate: – Hadamard gate: Z Y H

Summary of Simple Gates X Y Z H

Reversibility Requirement l l l All quantum operations have to be reversible Boolean operations are not necessarily so A reversible operation is always given by a unitary matrix, i. e. one for which:

The Controlled NOT Gate l l The CNOT gate is the standard two-qubit quantum gate It is defined like this:

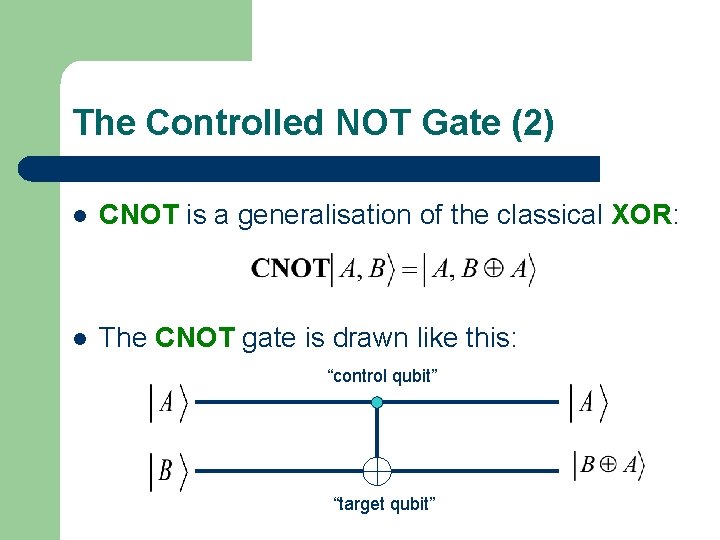
The Controlled NOT Gate (2) l CNOT is a generalisation of the classical XOR: l The CNOT gate is drawn like this: “control qubit” “target qubit”

The Controlled NOT Gate (3) l The matrix corresponding to the CNOT gate is: l The CNOT together with the single qubit gates are universal for quantum computing

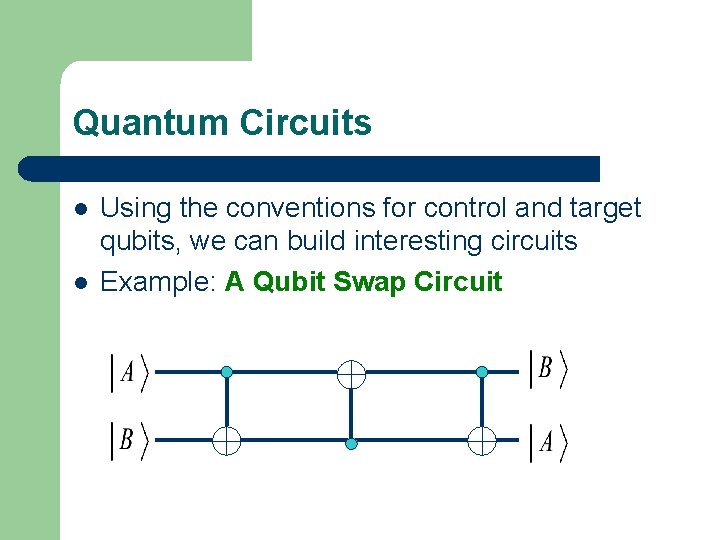
Quantum Circuits l l Using the conventions for control and target qubits, we can build interesting circuits Example: A Qubit Swap Circuit

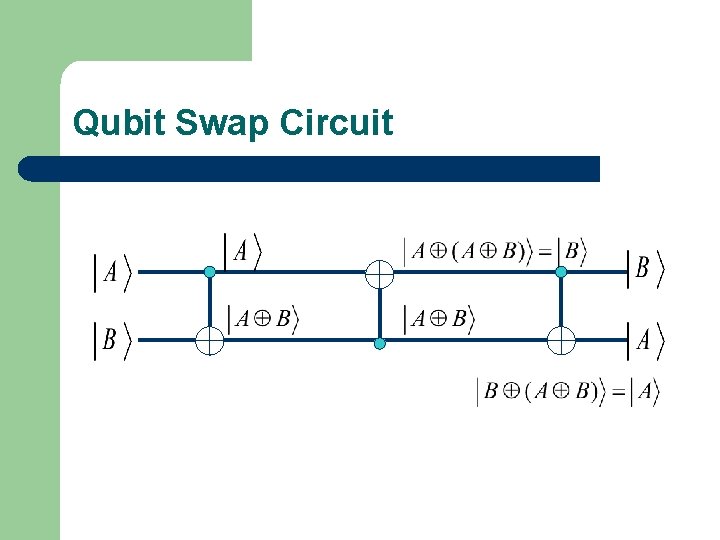
Qubit Swap Circuit

Features of Quantum Circuits 2. No loops are allowed; quantum circuits are acyclic Fan-in is not allowed: 3. Fan-out is not allowed: 1.

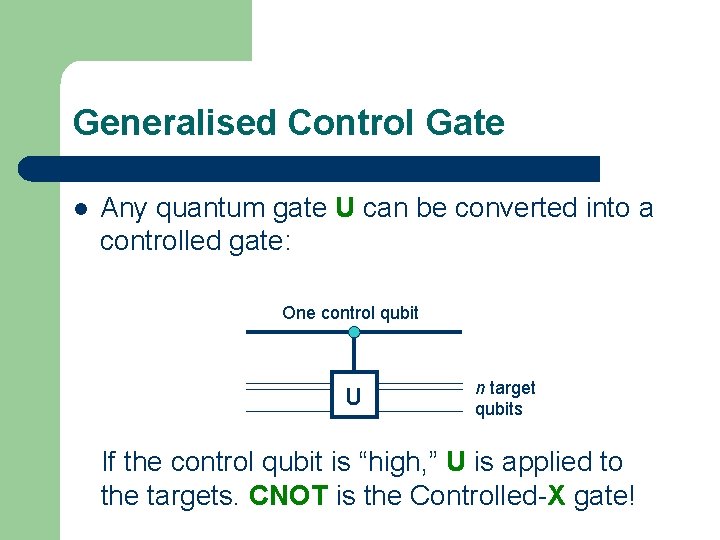
Generalised Control Gate l Any quantum gate U can be converted into a controlled gate: One control qubit U n target qubits If the control qubit is “high, ” U is applied to the targets. CNOT is the Controlled-X gate!

Quantum Measurement l Measurement in a quantum circuit is drawn as: M (classical bit representing outcome of measurement) If then: M = 0 with prob. or M = 1 with prob.

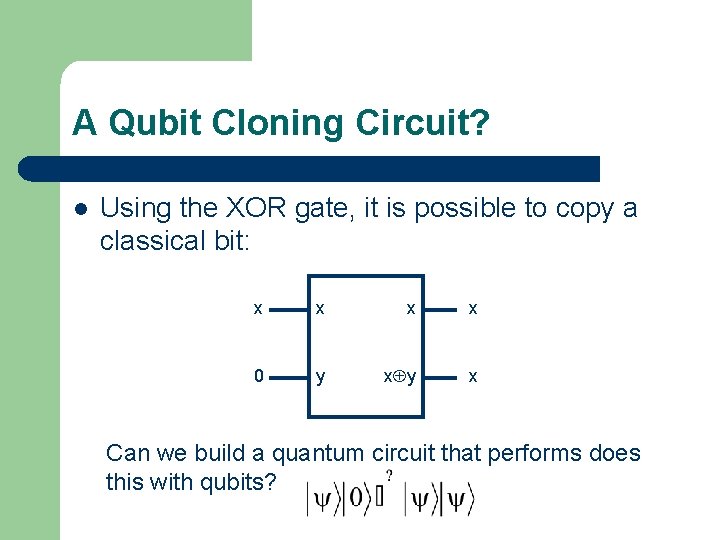
A Qubit Cloning Circuit? l Using the XOR gate, it is possible to copy a classical bit: x x 0 y xÅy x Can we build a quantum circuit that performs does this with qubits?

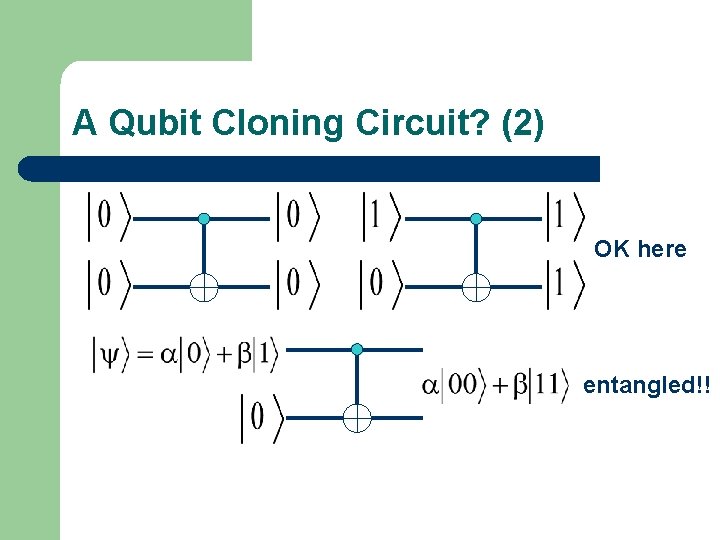
A Qubit Cloning Circuit? (2) OK here entangled!!

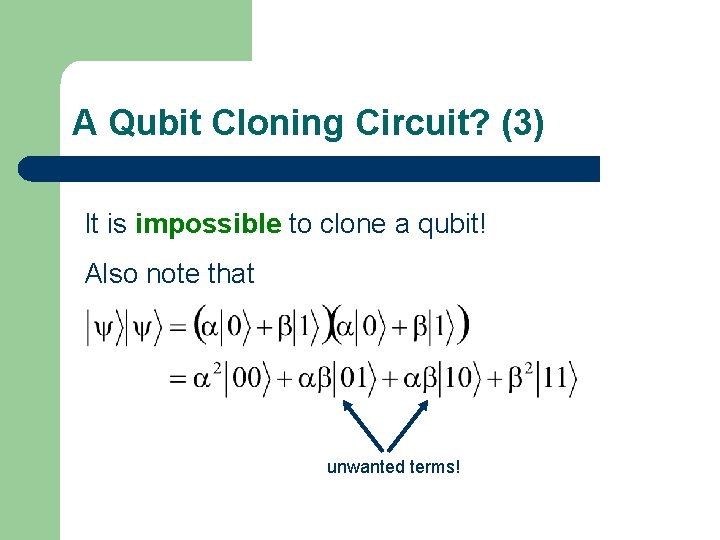
A Qubit Cloning Circuit? (3) It is impossible to clone a qubit! Also note that unwanted terms!

The Bell State Circuit x y H x y Output

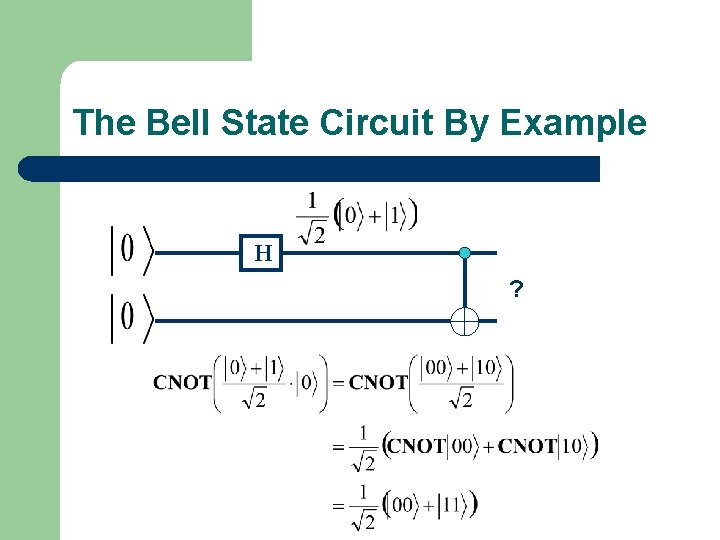
The Bell State Circuit By Example H ?

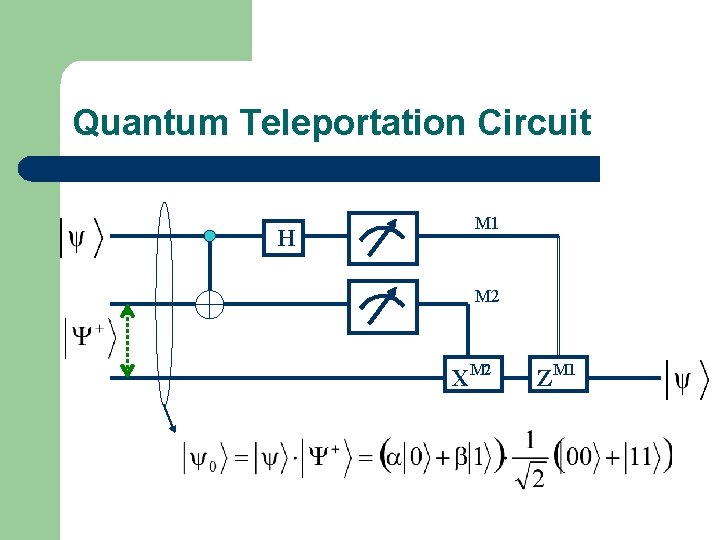
Quantum Teleportation Circuit H M 1 M 2 XM 2 ZM 1

Quantum Teleportation Circuit (2) H M 1 M 2 XM 2 ZM 1

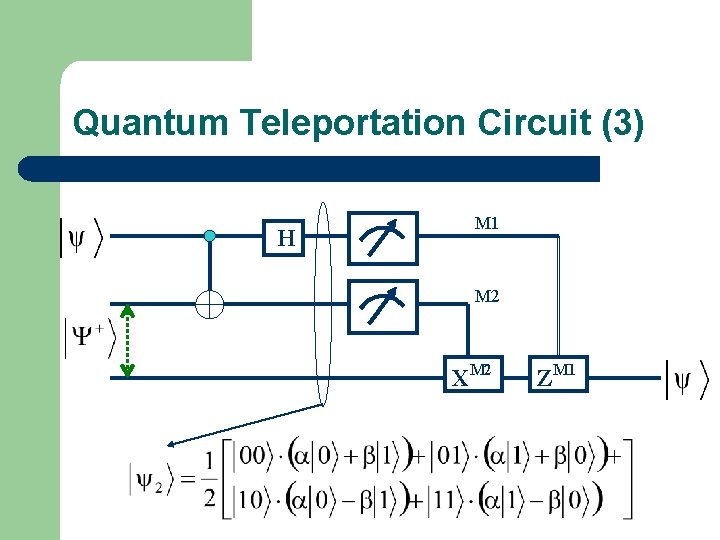
Quantum Teleportation Circuit (3) H M 1 M 2 XM 2 ZM 1

Quantum Teleportation Circuit (4) H M 1 M 2 XM 2 00, 01, 10 or 11 ZM 1

Quantum Teleportation Circuit (5) If Alice Then Bob’s obtains qubit is in state So Bob applies gate 00 I 01 X 10 Z 11 Y = ZX obtaining

What have we achieved? l l l The teleportation process makes it possible to “reproduce” a qubit in a different location But the original qubit is destroyed! Next topic: Quantum Parallelism and Deutsch’s quantum algorithm

Quantum Parallelism l l Quantum parallelism is that feature of quantum computers which makes it possible to evaluate a function f(x) on many different values of x simultaneously We will look at an example of quantum parallelism now – how to compute f(0) and f(1) for some function f all in one go!

Quantum Circuits for Boolean Functions l It is known that, for any boolean function l it is possible to construct a quantum circuit Uf that computes it Specifically, to each binary function f corresponds a quantum circuit: l binary addition

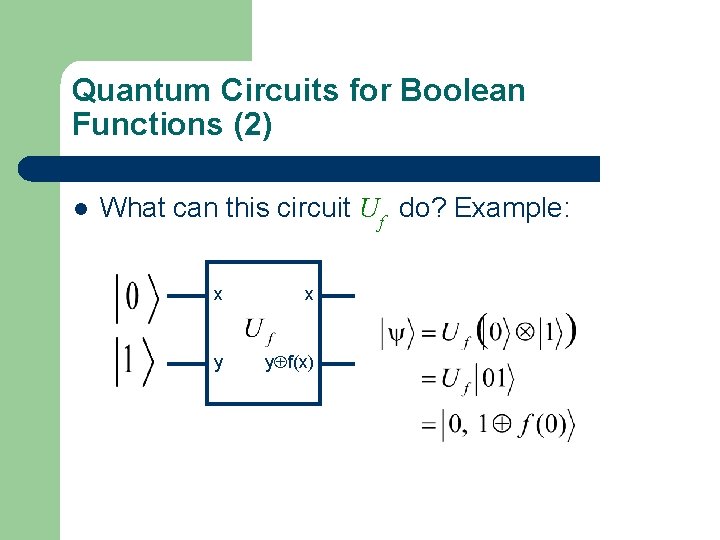
Quantum Circuits for Boolean Functions (2) l What can this circuit Uf do? Example: x x y yÅf(x)

Quantum Circuits for Boolean Functions (3) l But what if the input is a superposition? x x y yÅf(x) amazing! we’ve computed f(0) and f(1) at the same time!

Quantum Parallelism Summary l l So, a superposition of inputs will give a superposition of outputs! We can perform many computations simultaneously This is what makes famous quantum algorithms, such as Shor’s algorithm for factoring, or Grover’s algorithm for searching Simple q. algorithm: Deutsch’s algorithm

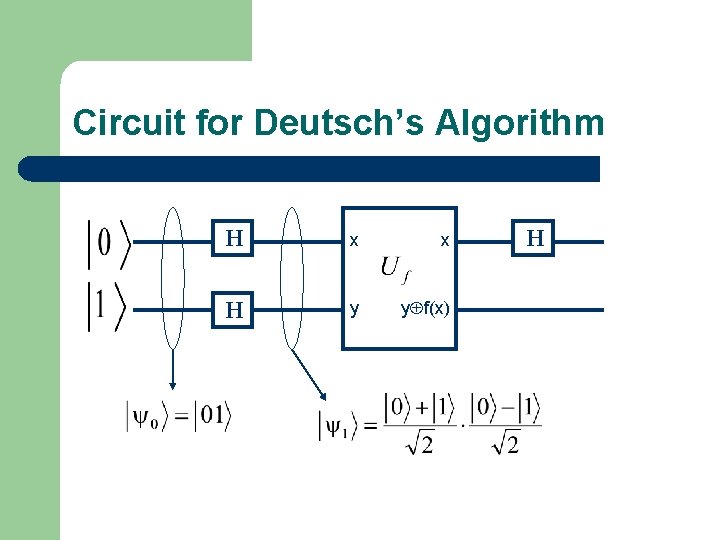
Deutsch’s Algorithm l David Deutsch: famous British physicist Deutsch’s algorithm allows us to compute, in only one step, the value of l To do this classically, you would have to: l 1. 2. 3. 1. compute f(0) compute f(1) add the two results Remember:

Circuit for Deutsch’s Algorithm H x x H y yÅf(x) H

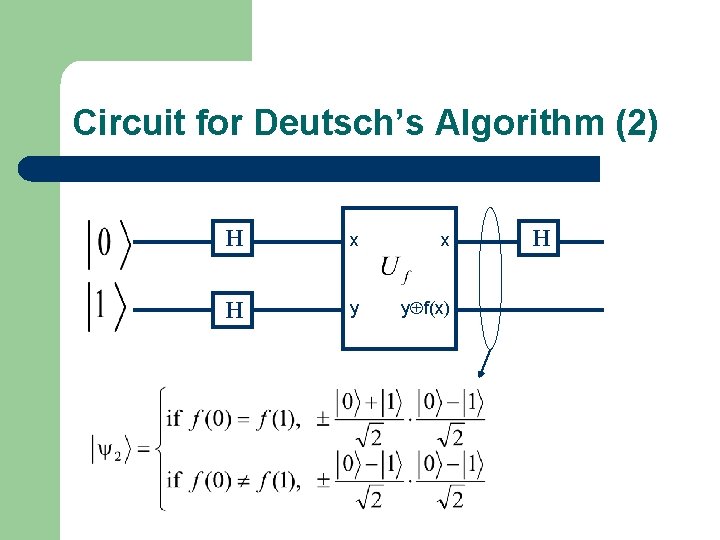
Circuit for Deutsch’s Algorithm (2) H x x H y yÅf(x) H

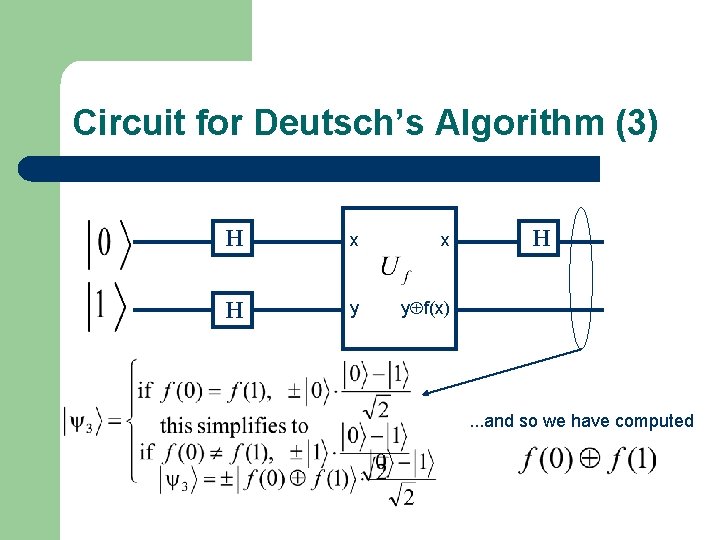
Circuit for Deutsch’s Algorithm (3) H x x H y yÅf(x) H . . . and so we have computed

End of Lecture 3 l Congratulations! If you are still awake, you have learned something about: – – – quantum gates (X, Y, Z, H, CNOT) quantum circuits (swapping, no-cloning problem) teleportation quantum parallelism and Deutsch’s algorithm