Quantum Computation and Quantum Information Lecture 2 Part

Quantum Computation and Quantum Information – Lecture 2 Part 1 of CS 406 – Research Directions in Computing Dr. Rajagopal Nagarajan Assistant: Nick Papanikolaou

Lecture 2 Topics l l l l Physical systems on the atomic scale State vectors and basis states; Qubits Systems of many qubits Quantum Measurement Entanglement Quantum gates Quantum coin-flipping and teleportation

Quantum physics and Nature l l l There exists a vast array of minute objects on the atomic scale: electrons, protons, neutrons, photons, quarks, neutrinos, … Quantum mechanics is a system of laws that describes the behaviour of such objects With computer chips getting smaller and smaller, by 2020 we will store 1 bit of data on objects of that size!

Quantum physics and Nature (2) l l Atom-sized objects behave in unusual ways; their “state” is generally unknown at any given time, and changes if you try to observe it! Several properties of these systems can be manipulated and measured.

Qubits l l A qubit is any quantum system with exactly two degrees of freedom; we use them to represent binary ‘ 0’ and ‘ 1’ Hydrogen atom: Ground state: l Excited state: Spin-1/2 electron: Spin-down (-ħ/2) state: Spin-up (+ħ/2) state:

Qubits (2) l l l In general, the state of a qubit is a combination, or superposition, of two basis states The rest state and the excited state are the basis states of the hydrogen atom The spin-up and spin-down states are basis states for the spin-1/2 particle

The State Vector l l The state of a quantum system is described by a state vector, written |yñ If the basis states for a qubit are written |0ñ and |1ñ, then the state vector for the qubit is |yñ = a |0ñ + b |1ñ where a and b are complex numbers with a 2 + b 2 = 1

Basis States l l Instead of |0ñ and |1ñ we can use any other basis states, as long as we can distinguish clearly between the two. Mathematically, basis states must be given by orthogonal vectors. |1ñ The inner product of the two vectors must be 0: |0ñ á 0 | 1ñ = 0

Basis states (2) l For example, we could use the basis {|+ñ, |-ñ} to describe the state of a qubit: |1ñ |-ñ Now: |yñ = g |+ñ + d |-ñ |+ñ |0ñ orthogonality: á+ | -ñ = 0

Systems of many qubits l If we know the individual states of the electrons in the system below: |y 1ñ = 0 |0ñ + 1 |1ñ = |1ñ 1 l 2 3 |y 2ñ = 1 |0ñ + 0 |1ñ = |0ñ |y 3ñ = 0 |0ñ + 1 |1ñ = |1ñ. . . then what is the overall state of the threeparticle system?

Systems of many qubits (2) l The state of a composite quantum system, when all the component states are known, is their tensor product: |yñ = |y 1ñ Ä |y 2ñ Ä |y 3ñ l l This is the “outer product” of vectors Note that this is different from the inner product áf½cñ

Systems of many qubits (3) l We have |yñ = |y 1ñ Ä |y 2ñ Ä |y 3ñ = (0 |0ñ + 1 |1ñ) Ä (1 |0ñ + 0 |1ñ) Ä (0 |0ñ + 1 |1ñ) = |1ñ Ä |0ñ Ä |1ñ By convention, we write |1ñ Ä |0ñ Ä |1ñ as |101ñ

Quantum Measurement l l To extract any information out of a quantum system, you have to perform a physical measurement By measuring a quantum system: – – you automatically change its state, the very state you’re trying to measure you obtain, in general, a random result, which may be different from the original state

Quantum Measurement (2) l l l When you try to measure a qubit |yñ = a |0ñ + b |1ñ. . . you will never be able to obtain the values of a and b. A measurement has to be made with respect to a particular basis.

Quantum Measurement (3) l If you measure with respect to the {|0ñ, |1ñ} basis: – – – l if |yñ = |0ñ the answer will be |0ñ with probability 100% if |yñ = |1ñ the answer will be |1ñ with probability 100% in all other cases (e. g. a 2=b 2=0. 5), the result will be probabilistic. After measurement, the value of |yñ will change permanently to the result obtained.

Quantum Measurement (4) l l l If you measure with respect to a different basis, things are worse! Measuring |yñ = a |0ñ + b |1ñ with respect to {|+ñ, |-ñ} will give one of the results |+ñ and |-ñ with particular probabilities. Also, the value of |yñ will change permanently to the result obtained.

Quantum Measurement, Formally, when you measure |yñ = a |0ñ + b |1ñ with respect to {|0ñ, |1ñ} you will get: l – – l result |0ñ with probability |a|2 result |1ñ with probability |b|2 If you use a different measurement basis, the result will be one of the basis states, with different probabilities

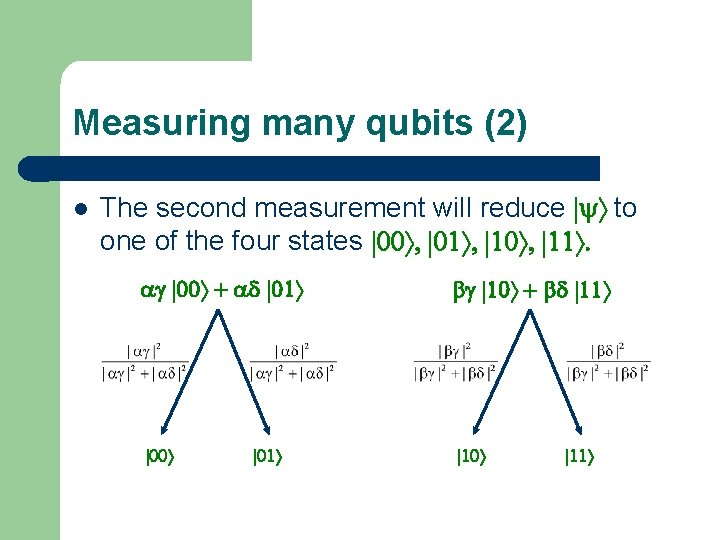
Measuring many qubits l We want to know the possible outcomes of measuring the two qubit state: |yñ = (a |0ñ + b |1ñ) Ä (g |0ñ + d |1ñ) = = ag |00ñ + ad |01ñ + bg |10ñ + bd |11ñ prob. |ag|2 + |ad|2 prob. |bg|2 + |bd|2 the first measurement will reduce |yñ to one of these smaller states

Measuring many qubits (2) l The second measurement will reduce |yñ to one of the four states |00ñ, |01ñ, |10ñ, |11ñ. ag |00ñ + ad |01ñ |00ñ |01ñ bg |10ñ + bd |11ñ |10ñ |11ñ

Measuring many qubits (3) l l By multiplying the branches in the overall tree, we can obtain the probability of each result. So for the state |yñ = ag |00ñ + ad |01ñ + bg |10ñ + bd |11ñ two consecutive measurements will give – – result |00ñ with probability |ag|2 result |01ñ with probability |ad|2 result |10ñ with probability |bg|2 result |11ñ with probability |bd|2

Entanglement l l There exist states of many-qubit systems that cannot be broken down into a tensor product E. g. : there do not exist a, b, g, d for which m |00ñ + n |11ñ = (a |0ñ + b |1ñ) Ä (g |0ñ + d |1ñ) These are termed entangled states.

The Bell states l For a two-qubit system, the four possible entangled states are named Bell states:

Measuring Entangled States l After measuring an entangled pair for the first time, the outcome of the second measurement is known 100% |0ñ 1 |0ñ 0. 5 |1ñ 1 |1ñ

Review l Thus far we have seen: – – l how qubits are represented how many qubits can be combined together what happens when you measure one or more qubits where entangled pairs come from, and what happens when you measure them Now we will take a look at quantum gates

Quantum gates l l l As in classical computing, a gate is an operation on a unit of data, here: a qubit A quantum gate is represented by a matrix that may be applied to a state vector We will talk about this in more detail next time; for now we will look at some examples of commonly used quantum gates: – – – the Hadamard gate (H) the Pauli gates (I, σx, σy, σz) the Controlled Not (CNot)

The Hadamard gate l The Hadamard gate acts on one qubit, and places it in a superposition of |0ñ and |1ñ :

The Pauli gates l The Pauli gates act on one qubit, as follows: – phase shift, σz: σz(a |0ñ + b |1ñ) = a |0ñ - b |1ñ – bit flip, σx: σx(a |0ñ + b |1ñ) = a |1ñ + b |0ñ – phase shift and bit flip, σy: σy(a |0ñ + b |1ñ) = a |1ñ - b |0ñ – identity, I, does not change the input

The Controlled Not Gate l The CNot gate acts on two qubits: CNot( |00ñ ) = |00ñ CNot( |01ñ ) = |01ñ CNot( |10ñ ) = |11ñ CNot( |11ñ ) = |10ñ

Quantum Coin Flipping l Quantum coin flipping is based on the following game: – – – l Alice places a coin, head upwards in a box. Alice and Bob then take turns to optionally turn the coin over (without looking at it). At the end of the game, the box is opened and Bob wins if the coin is head upwards. In the quantum version of the game, the coin is a quantum state

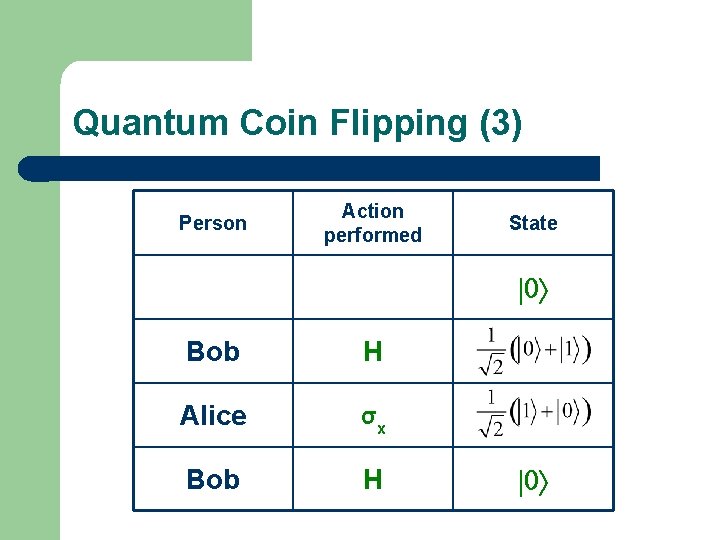
Quantum Coin Flipping (2) l Assume that Alice can only perform a flipping operation, i. e. gate σx Remember: σx(a |0ñ + b |1ñ) = a |1ñ + b |0ñ l l There is a strategy that allows Bob to win always: he must perform Hadamard operations. Thus Bob places the state of the coin in a superposition of “heads” and “tails”!

Quantum Coin Flipping (3) Person Action performed State |0ñ Bob H Alice σx Bob H |0ñ

The No-cloning principle l l It has been proved by Wootters and Zurek that it is impossible to clone, or duplicate, an unknown quantum state. However, it is possible to recreate a quantum state in a different physical location through the process of quantum teleportation.

Quantum Teleportation: The Basics l If Alice and Bob each have a single particle from an entangled pair, then: – – l It is possible for Alice to teleport a qubit to Bob, using only a classical channel The state of the original qubit will be destroyed How? – Using the properties of entangled particles

Quantum Teleportation l Alice wants to teleport particle 1 to Bob l Two particles, 2 and 3, are prepared in an entangled state l Particle 2 is given to Alice, particle 3 is given to Bob

Quantum Teleportation (2) l In order to teleport particle 1, Alice now entangles it with her particle using the CNot and Hadamard gates: l Thus, particle 1 is “disassembled” and combined with the entangled pair Alice measures particles 1 and 2, producing a classical outcome: 00, 01, 10 or 11. l

Quantum Teleportation l l l Depending on the outcome of Alice’s measurement, Bob applies a Pauli operator to particle 3, “reincarnating” the original qubit If outcome=00, Bob uses operator I If outcome=01, Bob uses operator σx If outcome=11, Bob uses operator σy If outcome=10, Bob uses operator σz Bob’s measurement produces the original state of particle 1.

Quantum Teleportation (Summary) l l l The basic idea is that Alice and Bob can perform a sequence of operations on their qubits to “move” the quantum state of a particle from one location to another The actual operations are more involved than we have presented here; see the standard texts on quantum computing for details Recommended: S. Lomonaco, “A Rosetta Stone for Quantum Computation” [see www]

Review l l Quantum gates allow us to manipulate quantum states without measuring them Quantum states cannot be cloned Teleportation allows a quantum state to be recreated by exchanging only 2 bits of classical information Quantum coin flipping is more fun than classical coin flipping!