Quantum coherence and interactions in many body systems

Quantum coherence and interactions in many body systems Eugene Demler Harvard University Collaborators: Ehud Altman, Anton Burkov, Derrick Chang, Adilet Imambekov, Vladimir Gritsev , Mikhail Lukin, Giovanna Morigi, Anatoli Polkonikov Funded by NSF, AFOSR, Harvard-MIT CUA

Condensed Atomic matter physics Quantum physics coherence Quantum optics Quantum information

Quantum Optics with atoms and Condensed Matter Physics with photons Interference of fluctuating condensates From reduced contrast of fringes to correlation functions Distribution function of fringe contrast Non-equilibrium dynamics probed in interference experiments Luttinger liquid of photons Can we get “fermionization” of photons? Non-equilibrium coherent dynamics of strongly interacting photons

Interference experiments with cold atoms

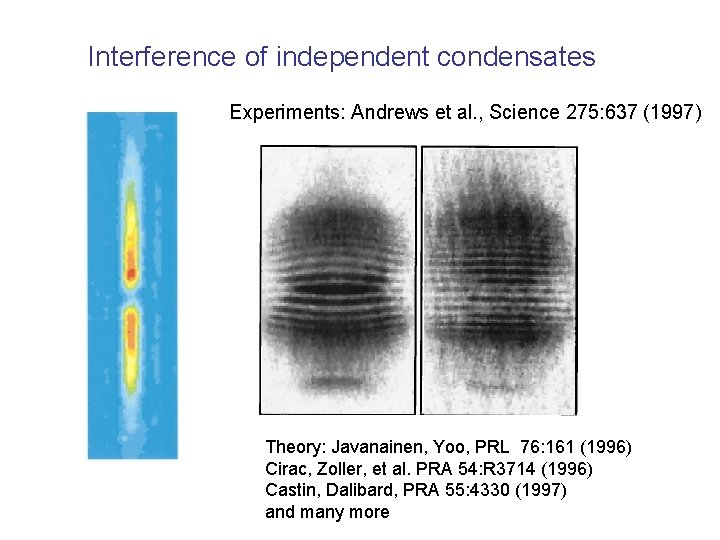
Interference of independent condensates Experiments: Andrews et al. , Science 275: 637 (1997) Theory: Javanainen, Yoo, PRL 76: 161 (1996) Cirac, Zoller, et al. PRA 54: R 3714 (1996) Castin, Dalibard, PRA 55: 4330 (1997) and many more

Interference of two independent condensates r’ r 1 r+d d 2 Clouds 1 and 2 do not have a well defined phase difference. However each individual measurement shows an interference pattern

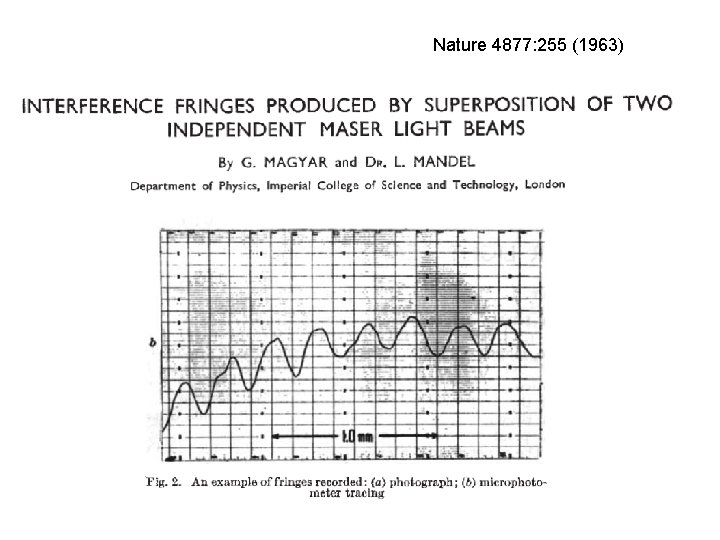
Nature 4877: 255 (1963)

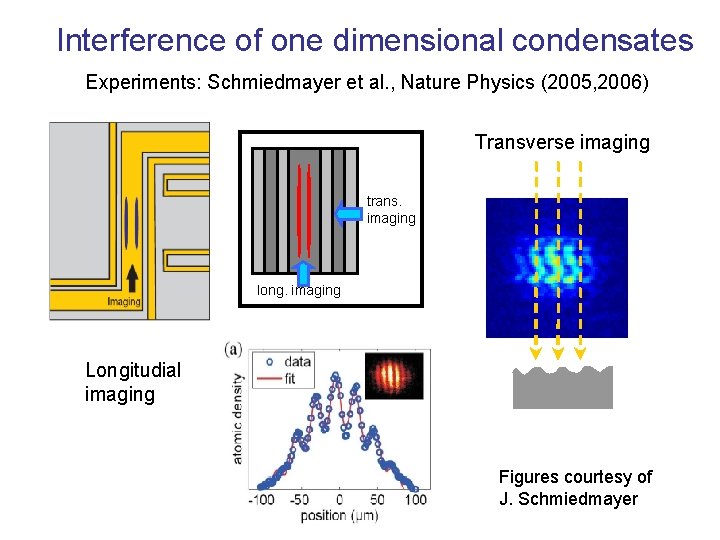
Interference of one dimensional condensates Experiments: Schmiedmayer et al. , Nature Physics (2005, 2006) Transverse imaging trans. imaging long. imaging Longitudial imaging Figures courtesy of J. Schmiedmayer

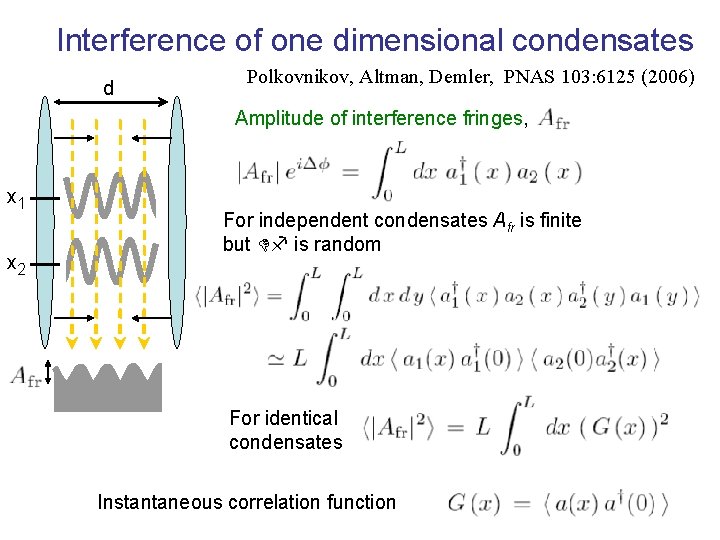
Interference of one dimensional condensates d Polkovnikov, Altman, Demler, PNAS 103: 6125 (2006) Amplitude of interference fringes, x 1 x 2 For independent condensates Afr is finite but Df is random For identical condensates Instantaneous correlation function

Interference of two dimensional condensates Experiments: Hadzibabic et al. Nature (2006) Gati et al. , PRL (2006) Ly Lx Lx Probe beam parallel to the plane of the condensates

Interference of two dimensional condensates. Quasi long range order and the KT transition Ly Lx Above KT transition Below KT transition

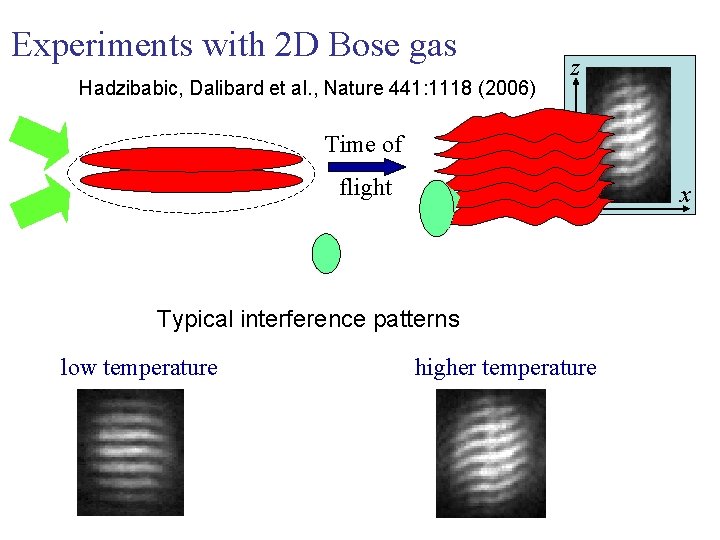
Experiments with 2 D Bose gas Hadzibabic, Dalibard et al. , Nature 441: 1118 (2006) z Time of flight x Typical interference patterns low temperature higher temperature

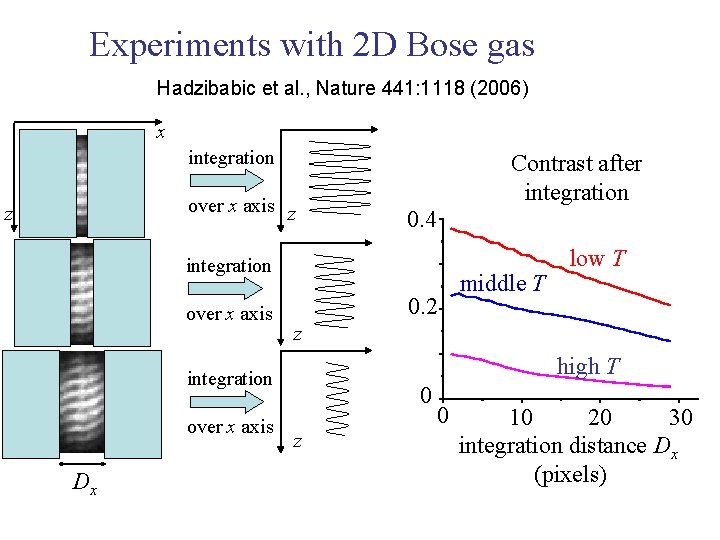
Experiments with 2 D Bose gas Hadzibabic et al. , Nature 441: 1118 (2006) x integration over x axis z z Contrast after integration 0. 4 integration over x axis 0. 2 z high T integration over x axis Dx middle T low T 0 z 0 10 20 30 integration distance Dx (pixels)

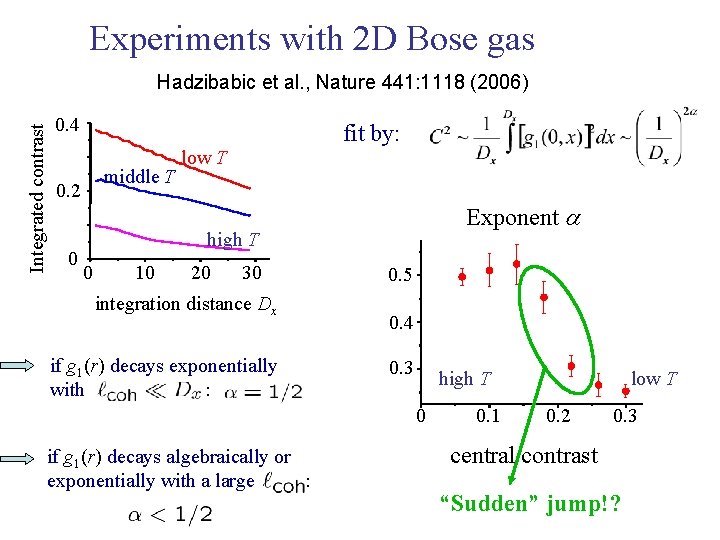
Experiments with 2 D Bose gas Integrated contrast Hadzibabic et al. , Nature 441: 1118 (2006) 0. 4 fit by: middle T 0. 2 0 low T Exponent a high T 0 10 20 30 integration distance Dx if g 1(r) decays exponentially with : 0. 5 0. 4 0. 3 high T 0 if g 1(r) decays algebraically or exponentially with a large : 0. 1 low T 0. 2 0. 3 central contrast “Sudden” jump!?

Fundamental noise in interference experiments Amplitude of interference fringes is a quantum operator. The measured value of the amplitude will fluctuate from shot to shot. We want to characterize not only the average but the fluctuations as well.

Shot noise in interference experiments Interference with a finite number of atoms. How well can one measure the amplitude of interference fringes in a single shot? One atom: No Very many atoms: Exactly Finite number of atoms: ? Consider higher moments of the interference fringe amplitude , , and so on Obtain the entire distribution function of

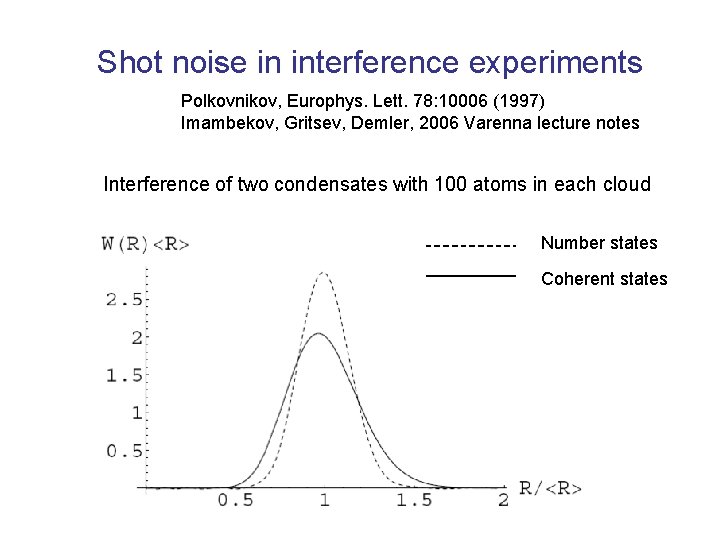
Shot noise in interference experiments Polkovnikov, Europhys. Lett. 78: 10006 (1997) Imambekov, Gritsev, Demler, 2006 Varenna lecture notes Interference of two condensates with 100 atoms in each cloud Number states Coherent states

Distribution function of fringe amplitudes for interference of fluctuating condensates Gritsev, Altman, Demler, Polkovnikov, Nature Physics (2006) Imambekov, Gritsev, Demler, cond-mat/0612011 L is a quantum operator. The measured value of will fluctuate from shot to shot. Higher moments reflect higher order correlation functions We need the full distribution function of

Interference of 1 d condensates at T=0. Distribution function of the fringe contrast Narrow distribution for. Approaches Gumbel distribution. Width Wide Poissonian distribution for

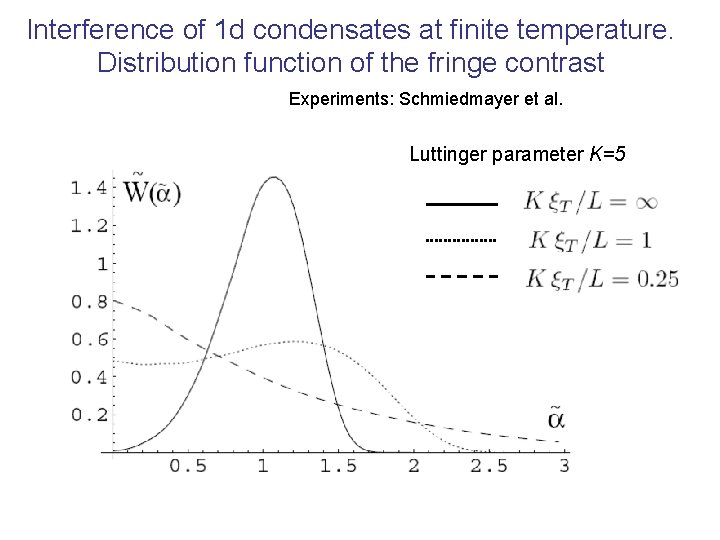
Interference of 1 d condensates at finite temperature. Distribution function of the fringe contrast Experiments: Schmiedmayer et al. Luttinger parameter K=5

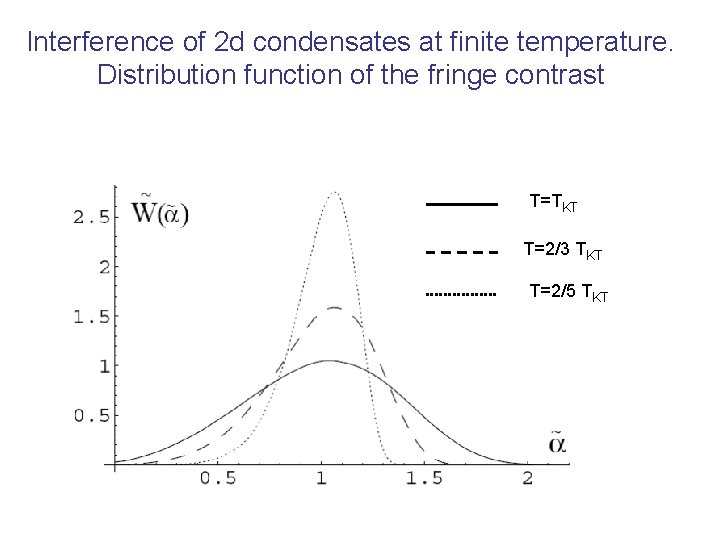
Interference of 2 d condensates at finite temperature. Distribution function of the fringe contrast T=TKT T=2/3 TKT T=2/5 TKT

From visibility of interference fringes to other problems in physics

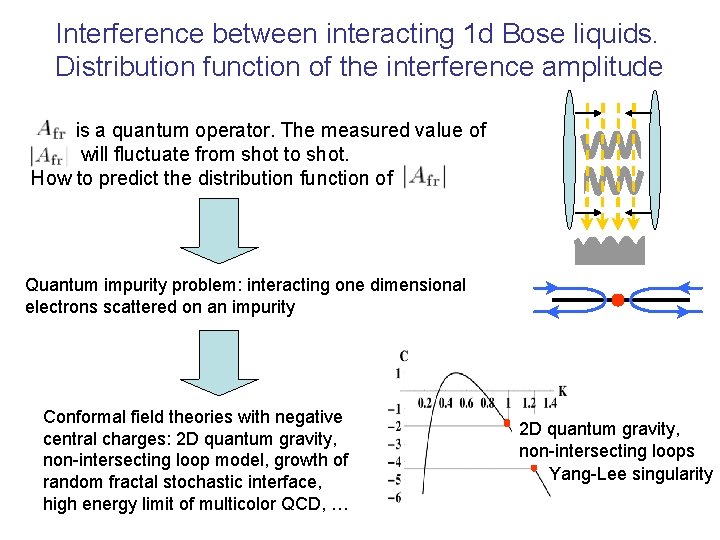
Interference between interacting 1 d Bose liquids. Distribution function of the interference amplitude is a quantum operator. The measured value of will fluctuate from shot to shot. How to predict the distribution function of Quantum impurity problem: interacting one dimensional electrons scattered on an impurity Conformal field theories with negative central charges: 2 D quantum gravity, non-intersecting loop model, growth of random fractal stochastic interface, high energy limit of multicolor QCD, … 2 D quantum gravity, non-intersecting loops Yang-Lee singularity

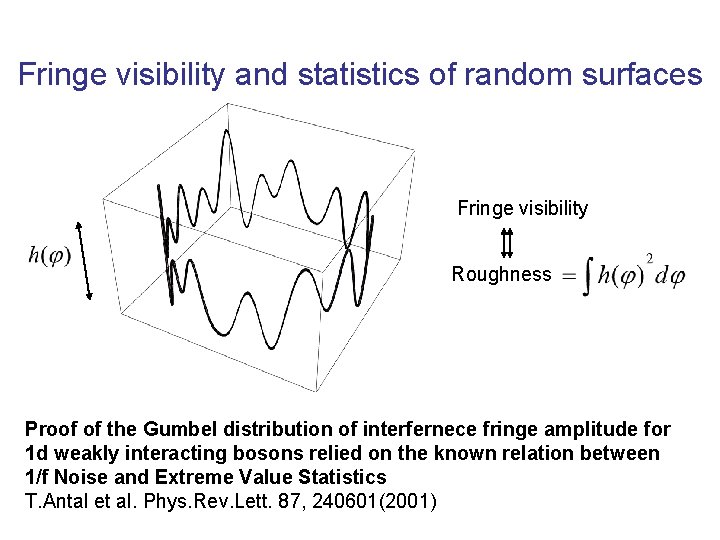
Fringe visibility and statistics of random surfaces Fringe visibility Roughness Proof of the Gumbel distribution of interfernece fringe amplitude for 1 d weakly interacting bosons relied on the known relation between 1/f Noise and Extreme Value Statistics T. Antal et al. Phys. Rev. Lett. 87, 240601(2001)

Non-equilibrium coherent dynamics of low dimensional Bose gases probed in interference experiments

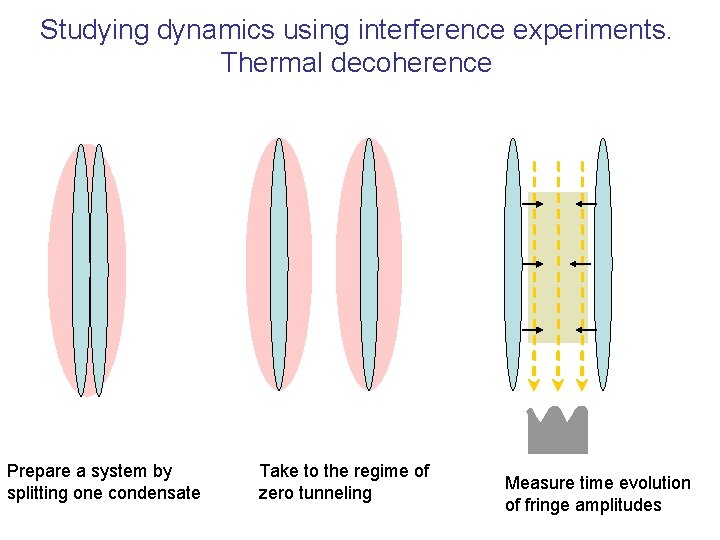
Studying dynamics using interference experiments. Thermal decoherence Prepare a system by splitting one condensate Take to the regime of zero tunneling Measure time evolution of fringe amplitudes

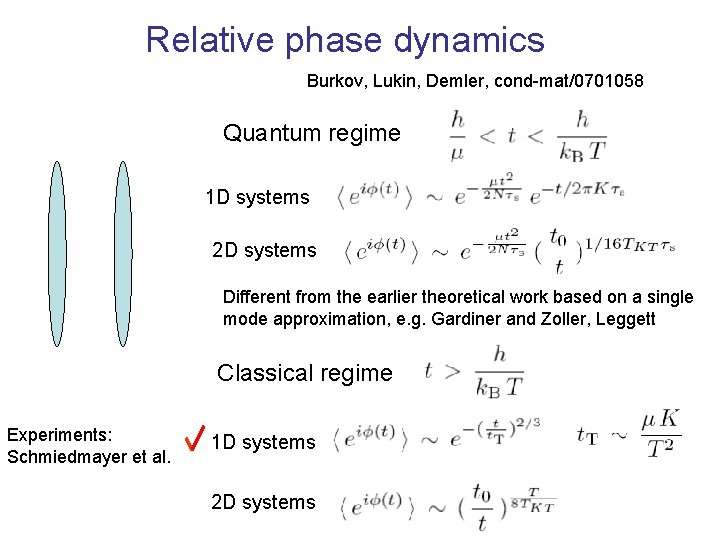
Relative phase dynamics Burkov, Lukin, Demler, cond-mat/0701058 Quantum regime 1 D systems 2 D systems Different from the earlier theoretical work based on a single mode approximation, e. g. Gardiner and Zoller, Leggett Classical regime Experiments: Schmiedmayer et al. 1 D systems 2 D systems

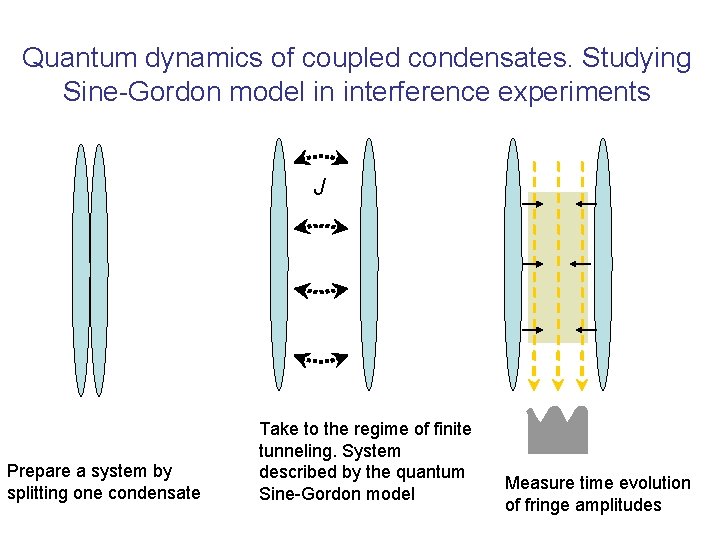
Quantum dynamics of coupled condensates. Studying Sine-Gordon model in interference experiments J Prepare a system by splitting one condensate Take to the regime of finite tunneling. System described by the quantum Sine-Gordon model Measure time evolution of fringe amplitudes

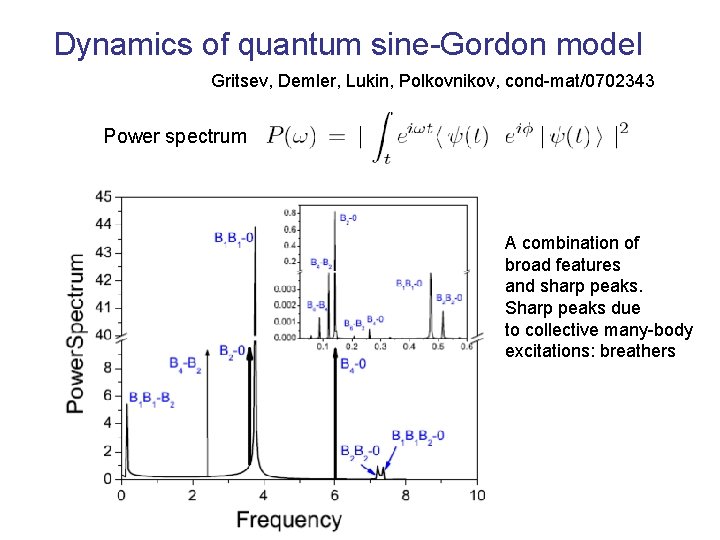
Dynamics of quantum sine-Gordon model Gritsev, Demler, Lukin, Polkovnikov, cond-mat/0702343 Power spectrum A combination of broad features and sharp peaks. Sharp peaks due to collective many-body excitations: breathers

Condensed matter physics with photons

Luttinger liquid of photons Tonks gas of photons: photon “fermionization” Chang, Demler, Gritsev, Lukin, Morigi, unpublished

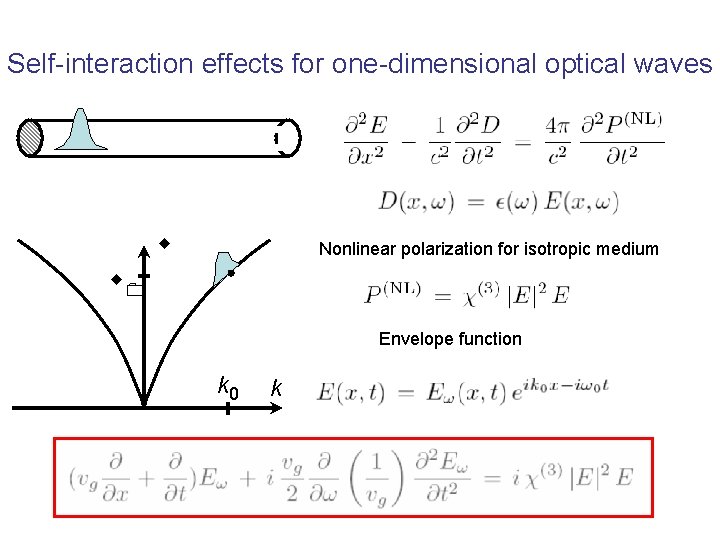
Self-interaction effects for one-dimensional optical waves w Nonlinear polarization for isotropic medium w 0 Envelope function k 0 k

Self-interaction effects for one-dimensional optical waves Frame of reference moving with the group velocity Gross-Pitaevskii type equation for light propagation Nonlinear Optics, Mills Competition of dispersion and non-linearity

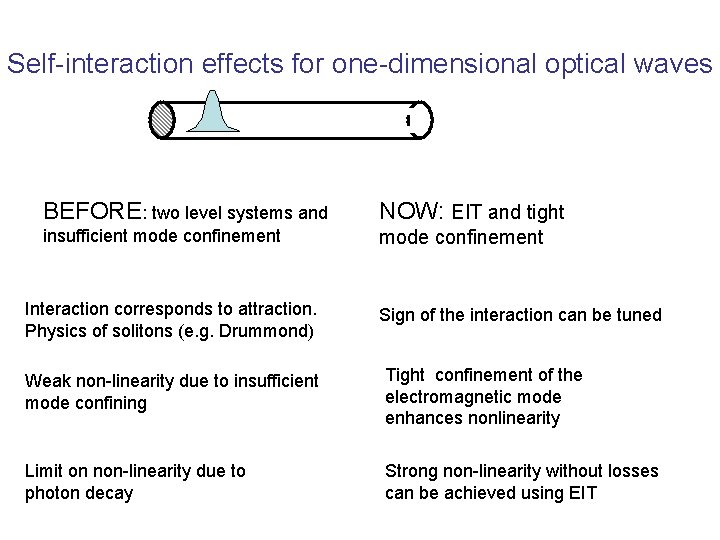
Self-interaction effects for one-dimensional optical waves BEFORE: two level systems and NOW: EIT and tight insufficient mode confinement Interaction corresponds to attraction. Physics of solitons (e. g. Drummond) Sign of the interaction can be tuned Weak non-linearity due to insufficient mode confining Tight confinement of the electromagnetic mode enhances nonlinearity Limit on non-linearity due to photon decay Strong non-linearity without losses can be achieved using EIT

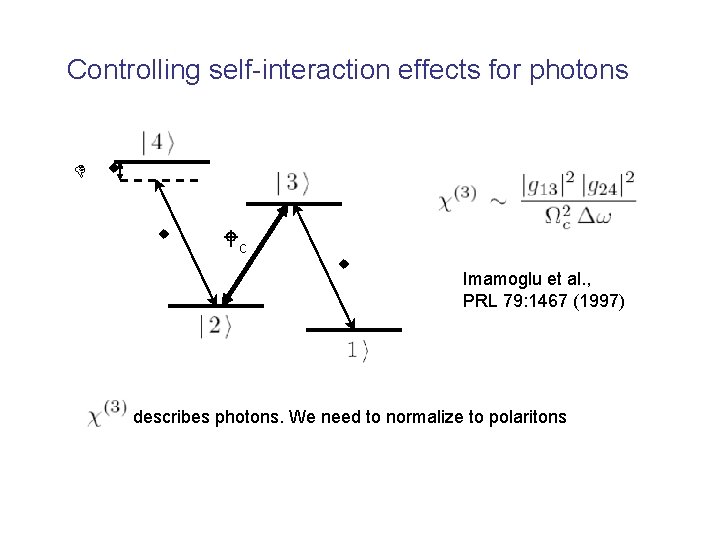
Controlling self-interaction effects for photons D w w Wc w Imamoglu et al. , PRL 79: 1467 (1997) describes photons. We need to normalize to polaritons

Tonks gas of photons Photon fermionization Crystal of photons Is it realistic? Experimental signatures

Tonks gas of atoms Small g – weakly interacting Bose gas Large g – Tonks gas. Fermionized bosons Additional effects for photons: Photons are moving with the group velocity Limit on the cross section of photon interacting with one atom

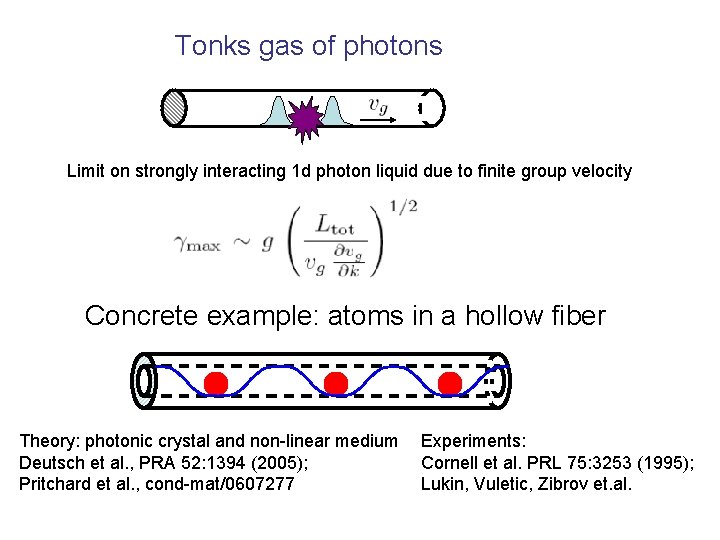
Tonks gas of photons Limit on strongly interacting 1 d photon liquid due to finite group velocity Concrete example: atoms in a hollow fiber Theory: photonic crystal and non-linear medium Deutsch et al. , PRA 52: 1394 (2005); Pritchard et al. , cond-mat/0607277 Experiments: Cornell et al. PRL 75: 3253 (1995); Lukin, Vuletic, Zibrov et. al.

Atoms in a hollow fiber w A – cross section of e-m mode Typical numbers l=1 mm A=10 mm 2 Ltot=1 cm k Without using the “slow light” points

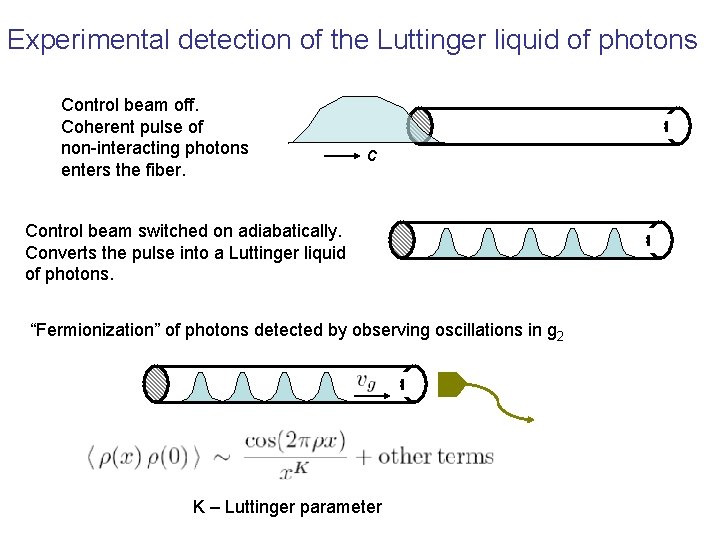
Experimental detection of the Luttinger liquid of photons Control beam off. Coherent pulse of non-interacting photons enters the fiber. c Control beam switched on adiabatically. Converts the pulse into a Luttinger liquid of photons. “Fermionization” of photons detected by observing oscillations in g 2 K – Luttinger parameter

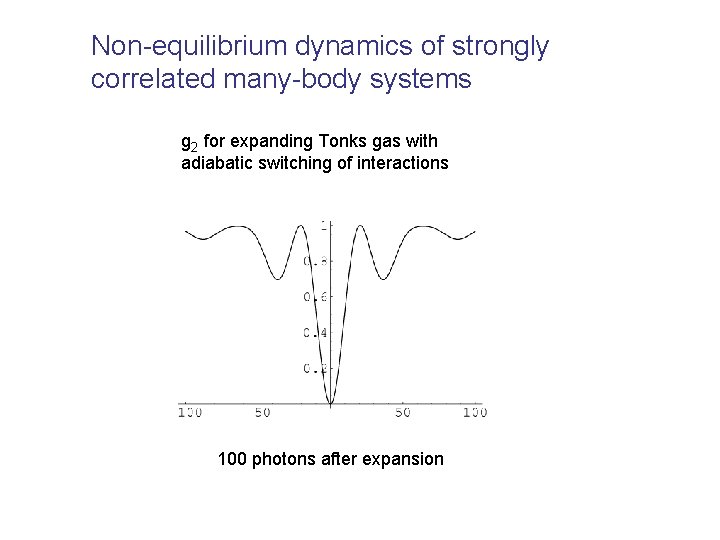
Non-equilibrium dynamics of strongly correlated many-body systems g 2 for expanding Tonks gas with adiabatic switching of interactions 100 photons after expansion

Outlook Next challenge in studying quantum coherence: understand non-equilibrium coherent quantum dynamics of strongly correlated many-body systems Atomic physics and quantum optics traditionally study non-equilibrium coherent quantum dynamics of relatively simple systems. Condensed matter physics analyzes complicated electron system but focuses on the ground state and small excitations around it. We will need the expertise of both fields “…The primary objective of the JQI is to develop a world class research institute that will explore coherent quantum phenomena and thereby lay the foundation for engineering and controlling complex quantum systems…” From the JQI web page http: //jqi. umd. edu/