Quantum Circuit Decomposition from unitary matrices into elementary

Prologue l l l In classical logic synthesis, one may trivially decompose any boolean

Objectives l Introduce the “controlled-U” gate – l l Exhibit a decomposition of a

References l The A. Barenko et. Al. paper, and how to write a controlled-U

The “controlled-U” l The block-matrix form of a “controlled-U” gate l These can be

One Qubit Rotations l Let U be a SU(2) matrix. U must take the

Some Quick Facts l R takes sums to products (R=Rz or Ry) l R(0)=I.

Circuit Decompositions l The A. Barenko et. Al. paper, and how to write a

Controlled-U Gates l Consider the “controlled-U” gate U l Claim: this circuit is equivalent

A B C Controlled-U Gates l Check this circuit on basis states l One

A B C Controlled-U Gates l Check this circuit on basis states l By

Controlled-U Gates l If U’ is in U(2) (as opposed to SU(2)), – l

Higher Order Controlled-U Gates l Recall (from two weeks ago) = U V V*

QR-Decomposition l Given a vector (a, b), this SU(2) matrix kills the second coordinate

QR-Decomposition l The vector (a, b) might be sitting inside a matrix: l Think

Making it a Circuit l The matrix used to kill coordinates in the bottom

QR-Decomposition l One may iterate this process

QR-Decomposition l This yields the formula – Where X was the original matrix, the

QR-Decomposition l l l If X is unitary, then R is the product of

Making it a Circuit l Need to make other planar rotations controlled-U gates l

Making it a Circuit l l Built the operator out of NOT and CNOT

Making it a Circuit l The general case is not much harder – –

Conclusion l l A unitary matrix can be written as a product of planar

Epilogue l l l The number of gates in this decomposition is exponential in

Reduction l l l Could try to shrink a long circuit by local optimization

Reduction l Could apply classical techniques…

Slides: 49

Download presentation

Quantum Circuit Decomposition from unitary matrices into elementary gates

Prologue l l l In classical logic synthesis, one may trivially decompose any boolean function into an OR of ANDs (sum of products) Local optimizations may then be applied to shrink the resulting circuit Can the same be done in the quantum case?

Objectives l Introduce the “controlled-U” gate – l l Exhibit a decomposition of a controlled-U into CNOT gates and 1 -qubit rotation gates Introduce the QR-decomposition Use QR to decompose a unitary matrix into controlled-U gates – Conclude that any operator can be built of CNOT gates and 1 -qubit rotations

References l The A. Barenko et. Al. paper, and how to write a controlled-U gate in elementary gates – – l U(2) and SU(2) matrices Controlled-U gates The Cybenko paper, and how to write an arbitrary unitary matrix in elementary gates – – QR decomposition Making it a circuit

The “controlled-U” l The block-matrix form of a “controlled-U” gate l These can be decomposed into – – CNOT gates 1 -qubit rotations

One Qubit Rotations l Let U be a SU(2) matrix. U must take the form l Where

One Qubit Rotations l Define l So that

Some Quick Facts l R takes sums to products (R=Rz or Ry) l R(0)=I. So: l Finally,

Circuit Decompositions l The A. Barenko et. Al. paper, and how to write a controlled-U gate in elementary gates – – l U(2) and SU(2) matrices Controlled-U gates The Cybenko paper, and how to write an arbitrary unitary matrix in elementary gates – – QR decomposition Making it a circuit

Controlled-U Gates l Consider the “controlled-U” gate U l Claim: this circuit is equivalent A B C

A B C Controlled-U Gates l Check this circuit on basis states l One observes

A B C Controlled-U Gates l Check this circuit on basis states l One observes l And similarly,

A B C Controlled-U Gates l Check this circuit on basis states l By linearity, this circuit performs “controlled-U”

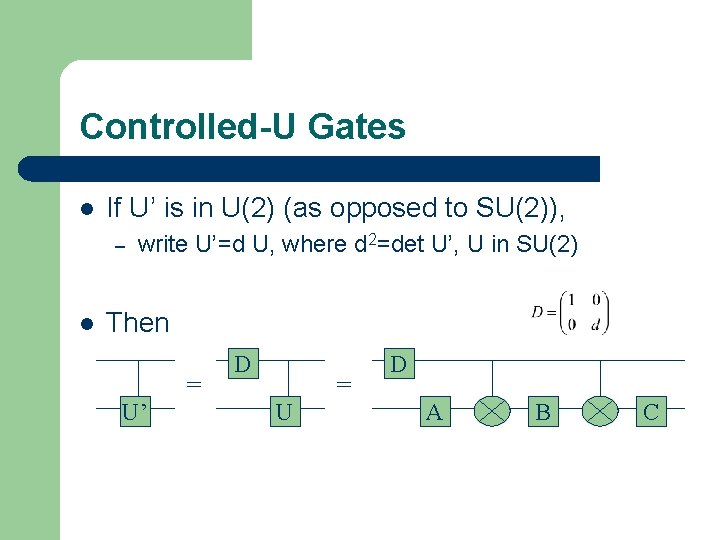
Controlled-U Gates l If U’ is in U(2) (as opposed to SU(2)), – l write U’=d U, where d 2=det U’, U in SU(2) Then = U’ D = U D A B C

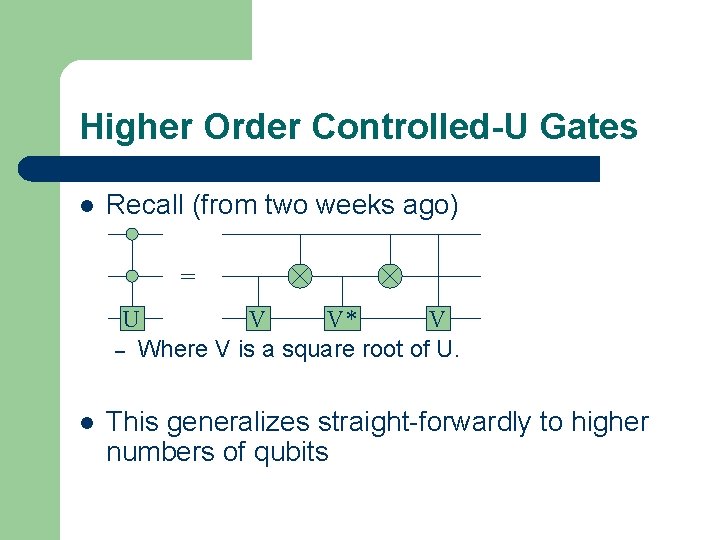
Higher Order Controlled-U Gates l Recall (from two weeks ago) = U V V* V – Where V is a square root of U. l This generalizes straight-forwardly to higher numbers of qubits

QR-Decomposition l Given a vector (a, b), this SU(2) matrix kills the second coordinate

QR-Decomposition l The vector (a, b) might be sitting inside a matrix: l Think of this as a rotation of the plane in which the 3 rd and 4 th coordinates live l Note that this matrix is unitary

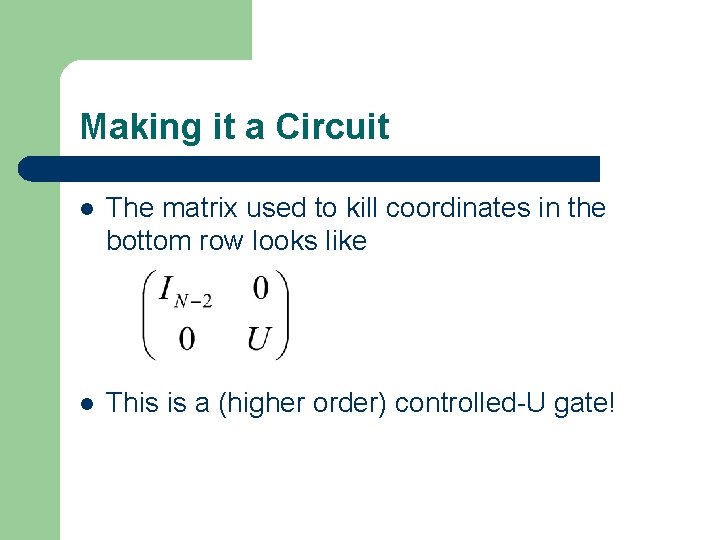
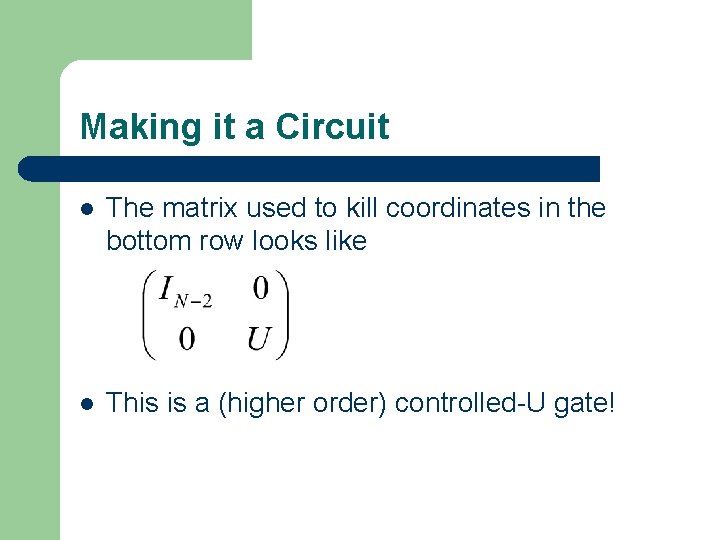
Making it a Circuit l The matrix used to kill coordinates in the bottom row looks like l This is a (higher order) controlled-U gate!

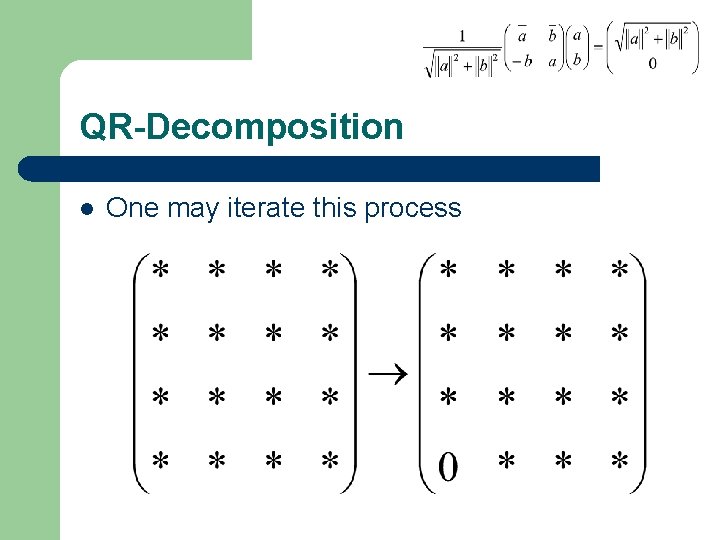
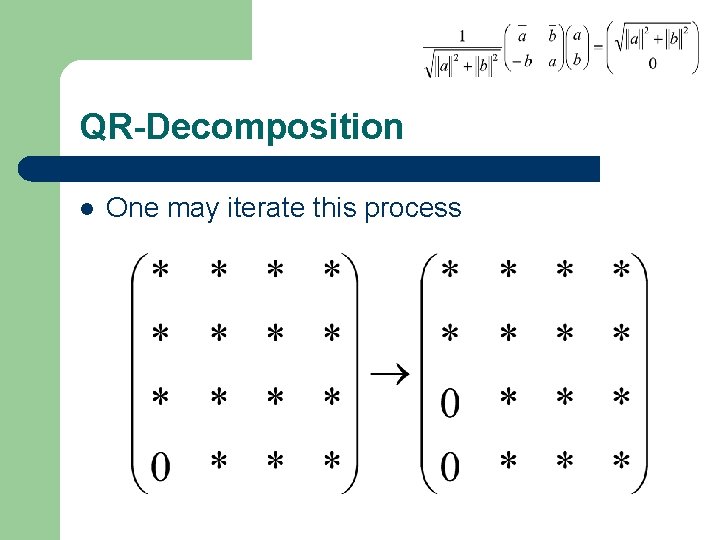
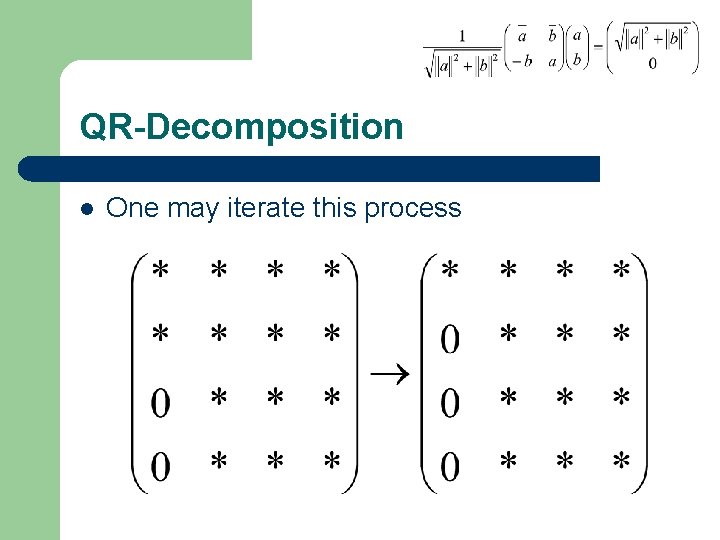
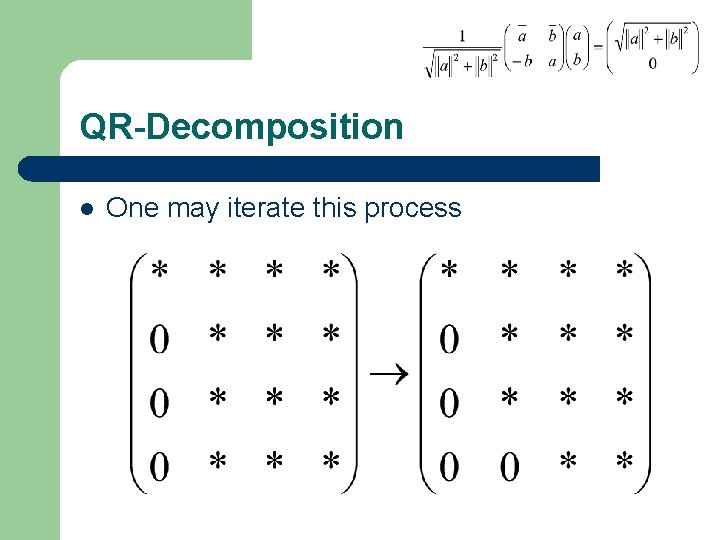
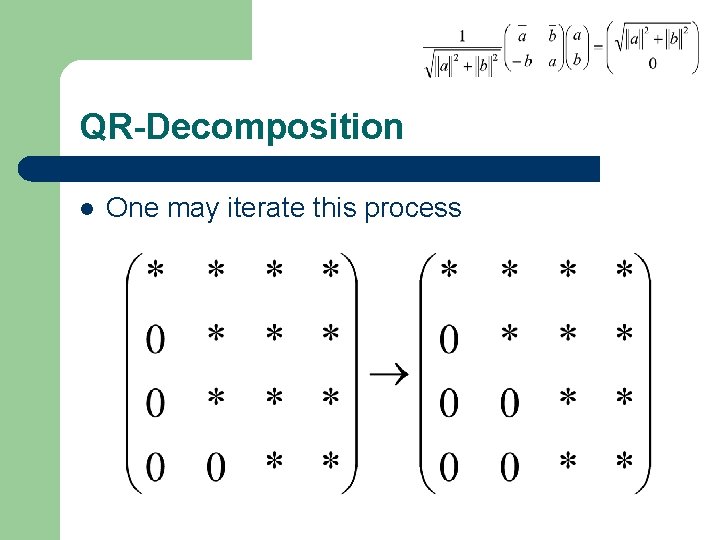
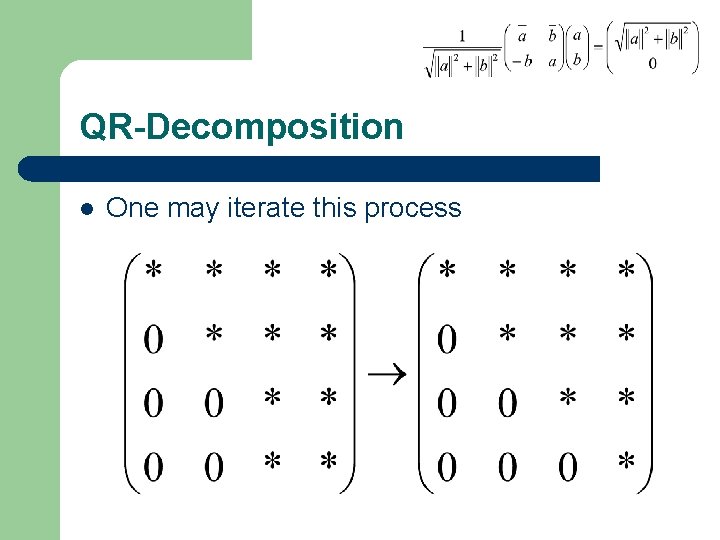
QR-Decomposition l One may iterate this process

QR-Decomposition l This yields the formula – Where X was the original matrix, the Ui are planar rotations, and R is upper triangular with nonnegative real entries on the diagonal

QR-Decomposition l Inverting the Q,

QR-Decomposition l l l If X is unitary, then R is the product of unitary matrices and hence unitary. A triangular unitary matrix must be diagonal A diagonal unitary matrix with nonnegative real entries must be the identity

Making it a Circuit l The matrix used to kill coordinates in the bottom row looks like l This is a (higher order) controlled-U gate!

Making it a Circuit l Need to make other planar rotations controlled-U gates l For some j, given an operator Pj l Pj. UPj-1 is a rotation in the j, j+1 plane. (where U is a rotation in the n-2, n-1 plane)

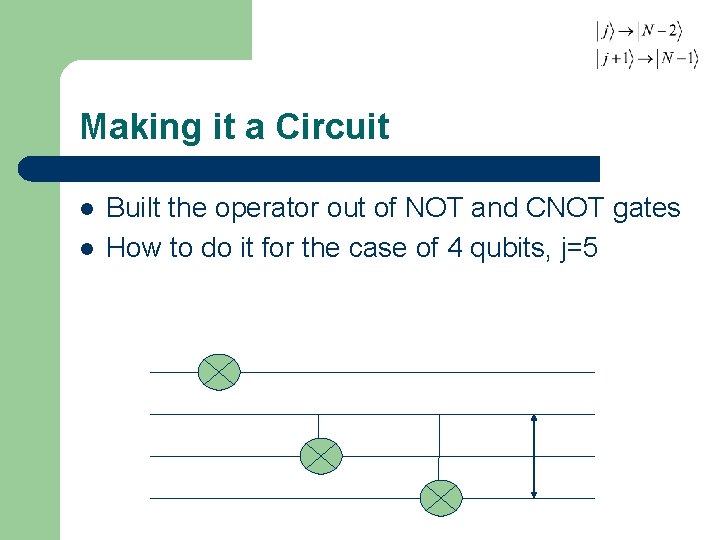
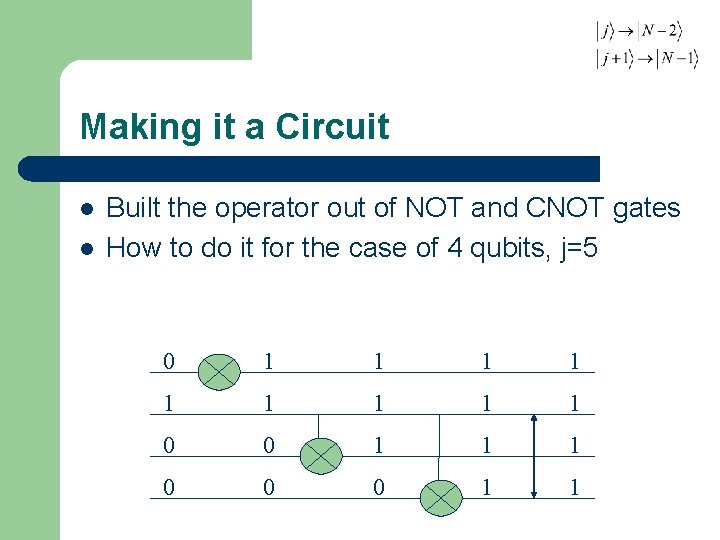
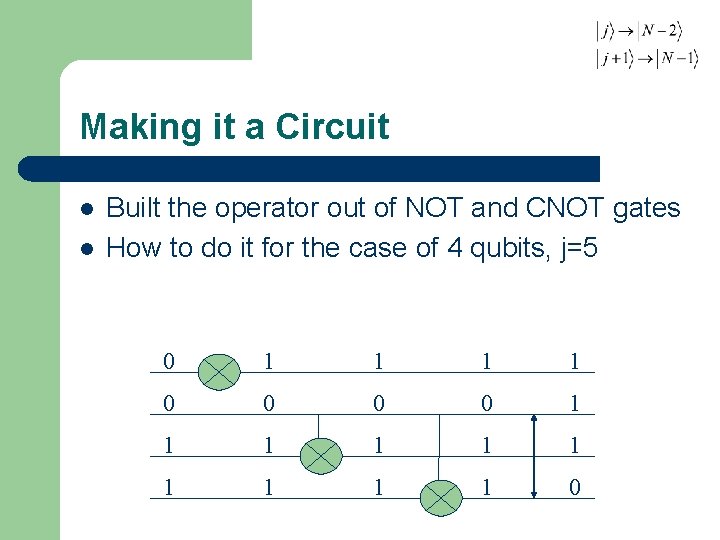
Making it a Circuit l l Built the operator out of NOT and CNOT gates How to do it for the case of 4 qubits, j=5

Making it a Circuit l l Built the operator out of NOT and CNOT gates How to do it for the case of 4 qubits, j=5 0 1 1 1 1 1 0 0 0 1 1

Making it a Circuit l l Built the operator out of NOT and CNOT gates How to do it for the case of 4 qubits, j=5 0 1 1 0 0 1 1 1 1 1 0

Making it a Circuit l The general case is not much harder – – – First, flip all bits that are 0 in both j, j+1 Then, CNOT every remaining bit that is zero in j+1, controlling by the unique bit that is 1 in j+1 and 0 in j Finally, switch this unique bit with the low bit

Conclusion l l A unitary matrix can be written as a product of planar rotations A planar rotation can be written as ZUZ-1, where Z can be decomposed into CNOT and NOT gates, and U is a (higher order) controlled-U gate A higher order controlled-U gate can be written as a sequence of CNOT gates and singly controlled-U gates A controlled-U gate can be written as a sequence of CNOT gates and one-qubit rotations

Epilogue l l l The number of gates in this decomposition is exponential in the number of qubits For certain operators, much smaller circuits are known to exist Can we automate the process of moving towards these?

Reduction l l l Could try to shrink a long circuit by local optimization techniques One experimentally observed obstacle: long chains of CNOT gates These long chains of CNOTs result from certain identities

Reduction l Could apply classical techniques…