Quantum angular momentum matrices eigenvalues and SVs Peter

Quantum angular momentum matrices – eigenvalues and SVs Peter Loly Department of Physics and Astronomy, University of Manitoba, Winnipeg WCLAM 14 -15 May 2016

Abstract • Replace “matrix norms” by “integer measures”.

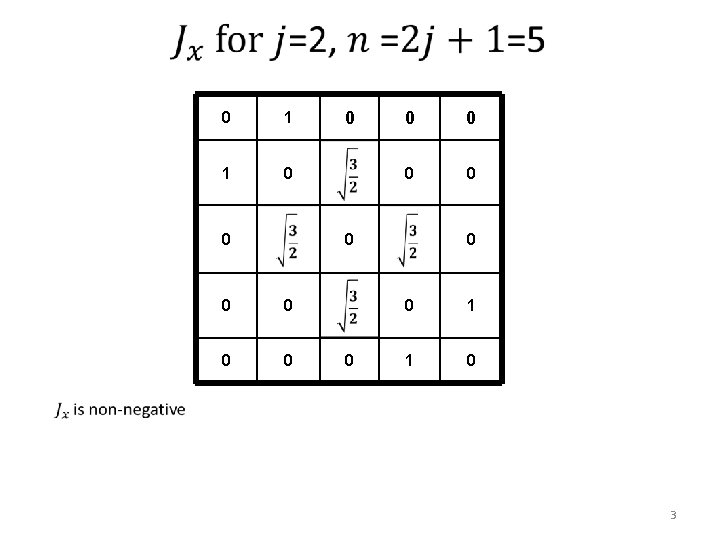
0 1 1 0 0 0 0 1 1 0 3

Google Search • • matrix mechanics -> IMAGES Many of these matrices appear there. Contemporary context includes “qubits”.

1925 Werner Heisenberg 91 st anniversary! Niels Bohr, “Copenhagen” – 1912 electron orbits June 1925 Heisenberg’s “matrix mechanics”, Uncertainty Principle. Paul Dirac 1925 November 7; and 16 th : Born, H and Jordan Wolfgang Pauli 1926/27 – spin 1/2 matrices, Exclusion Principle. 1926 Erwin Schrӧdinger’s “wave mechanics”, his “cat”. 1972 B. L. van der Waerden, Notices of the AMS, Nov. 1997, 323 -8. Note remarks on C. Lanczos. • Heisenberg just one of several students of Arnold Sommerfeld (Munich) - to win Nobel Prize. • Fritz London NOT! His student R. K. Eisenshitz, “Matrix Algebra for Physicists”, c. 1972, supervised my undergraduate dissertation on “The Theory of Measurement in Quantum Mechanics” in 1963. • • •

Spin ½ 1921 Stern-Gerlach experiment; • 1927 Pauli matrices

Background • Ph. D. – Interacting spin waves in Heisenberg’s model of ferromagnetism using many-body techniques (Green’s functions, quantum field theory at finite temperatures) for boson and spin models. • Much later teaching “Introduction to Theoretical Physics” with a chapter on matrices … numerical examples of simple matrices from MATLAB’s magic(n) function.

Overview My interest in these fundamental square matrices is in obtaining integer characteristic polynomials from which integer sums of eigenvalue and singular value powers follow. They include imaginary matrices, and matrices with no eigenvalues (j+, j-) where singular value analysis becomes essential. Previous work on integer matrices, especially Latin squares and magic squares.

Matrix sums • 1629 Albert Girard – powers of roots of polynomials • Later Newton’s identities • G. A. Miller 1909, and 1916, 1927

Girard’s identities 1629 •

Vector Model

General formulae (ħ =h/2π) (J. J. Sakurai, Modern Quantum Mechanics) •

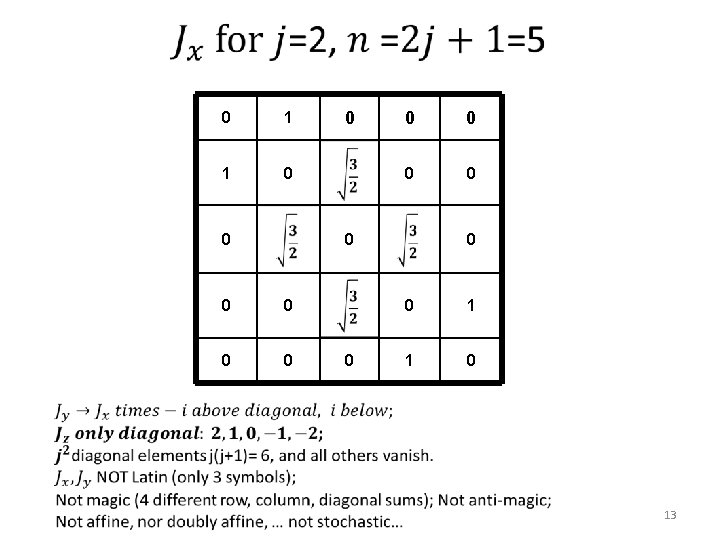
0 1 1 0 0 0 0 1 1 0 13

Sums •

n=2 j+1 j r EVs SVs 2 ½ 2 1, 1 2 2 3 1 2 2, 2, 0 8 32 4 3/2 4 3, 3, 1, 1 20 164 5 2 4 4, 4, 2, 2, 0 40 544 6 5/2 6 5, 5, 3, 3, 1, 1 70 1414 7 3 6 6, 6, 4, 4, 2, 2, 0 112 3136

EV 2 and SV 2 sums •

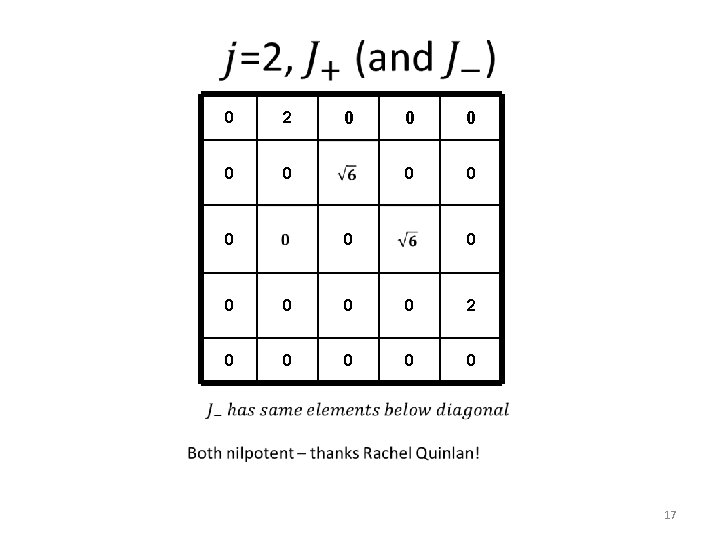
0 2 0 0 0 0 2 0 0 0 17

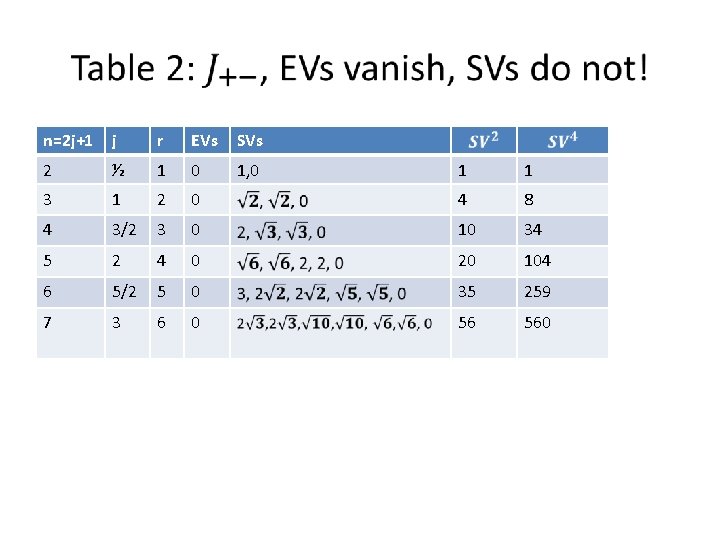
n=2 j+1 j r EVs SVs 2 ½ 1 0 1, 0 3 1 2 4 3/2 5 1 1 0 4 8 3 0 10 34 2 4 0 20 104 6 5/2 5 0 35 259 7 3 6 0 56 560

OEIS •

DISCLAIMER! • https: //en. wikipedia. org/wiki/Magic_number _(physics) • The seven most widely recognized magic numbers as of 2007 are 2, 8, 20, 28, 50, 82, and 126 (sequence A 018226 in OEIS).

End • Thanks to Andrew Senchuk, Adam Rogers • 12 May - Conjugate transpose used for jy… • Question: Are there other physics topics where singular values, sums of EVs and SVs, … might be useful?

LINSTAT-2012, IWMS-21 at Bedlewo, Poland http: //home. cc. umanitoba. ca/~loly/ -> NEWS 2013 in LATEST NEWS… • "Signatura of magic and Latin integer squares: isentropic clans and indexing. ” by Ian Cameron, Adam Rogers and Peter D. Loly, from 2012 conference published in Discussiones Mathematicae Probability and Statistics, 33(1 -2) (2013) 121 -149, from http: //www. discuss. wmie. uz. zgora. pl/ps" • “plain version of 2012 conference paper published in Discussiones Mathematicae Probability and Statistics, 33(1 -2) (2013) 121 -149. [DMPS] • “Data Appendix for Signatura”: Ian Cameron, Adam Rogers and Peter D. Loly

Some talks and papers on “magical squares” • • • LOLY, The Invariance of the Moment of Inertia of Magic Squares , The Mathematical Gazette, 88, March 2004, 151 -153. Daniel Schindel, Matthew Rempel and Peter LOLY, Enumerating the bent diagonal squares of Dr Benjamin Franklin FRS, Proceedings of the Royal Society A: Physical, Mathematical and Engineering, 462 (2006) 2271 -2279. LOLY, Franklin Squares: A Chapter in the Scientific Studies of Magical Squares, Complex Systems 17 (2007) 143 -161 from NKS 2006 (Wolfram-Mathematica). Eigenvalues in the Universe of Matrix Elements 1. . n-squared. IWMS-16 2007 – Introductory Keynote Talk (with Ian Cameron and Adam Rogers) – SVDs: Peter LOLY, Ian Cameron, Walter Trump and Daniel Schindel, Magic square spectra, Linear Algebra and its Applications, 430 (2009) WCLAM 2008 Winnipeg – Compound MS - Adam Rogers with Loly and Styan – Discussion - Loly: some are matrices with only the linesum EV of doubly stochastics. Cameron, Adam Rogers & Peter Loly, Signatura of magic and Latin integer squares: isentropic clans and indexing. , IWMS 2012 Bedlewo, Poland – VIDEO http: //www. physics. umanitoba. ca/~icamern/Poland 2012/ Discussiones Mathematicae Probability and Statistics, 33(1 -2) (2013) 121 -149. CMS 2014 Winnipeg – Multimagic (Knut Vik) Latin Squares with Cameron and Rogers WCLAM 2016 - now

Shannon Entropy and Magical Squares • Newton, P. K. & De. Salvo, S. A. (2010) [“NDS”] “The Shannon entropy of Sudoku matrices”, Proc. R. Soc. A 466: 1957 -1975 [Online Feb. 2010. ] • Immediately clear to us that we could extend NDS using our studies of the singular values of magic squares at IWMS 16 in 2007, published in Lin. Alg. Appl. 430 (10) 2659 -2680, 2009. • DMPS • http: //home. cc. umanitoba. ca/~loly/

Shannon Entropy •

Magic squares, Morse—Hedlund sequence, Hilbert-Kamke and Waring problems • Sergeyev, Y. D. , “Generation of symmetric exponential sums”, ar. Xiv: 1103. 2043 v 1 [math. NT] 10 Mar 2011

“Almost All Integer Matrices Have No Integer Eigenvalues”, Greg Martin and Erick B. Wong, UBC: • www. math. ubc. ca/~gerg/papers/downloads/ AAIMHNIE. pdf