Quantization Trac D Tran ECE Department The Johns

Quantization Trac D. Tran ECE Department The Johns Hopkins University Baltimore, MD 21218

Outline u u Review Quantization § Nonlinear mapping § Forward and inverse quantization § Quantization errors § Clipping error § Approximation error § Error model § Optimal scalar quantization § Examples

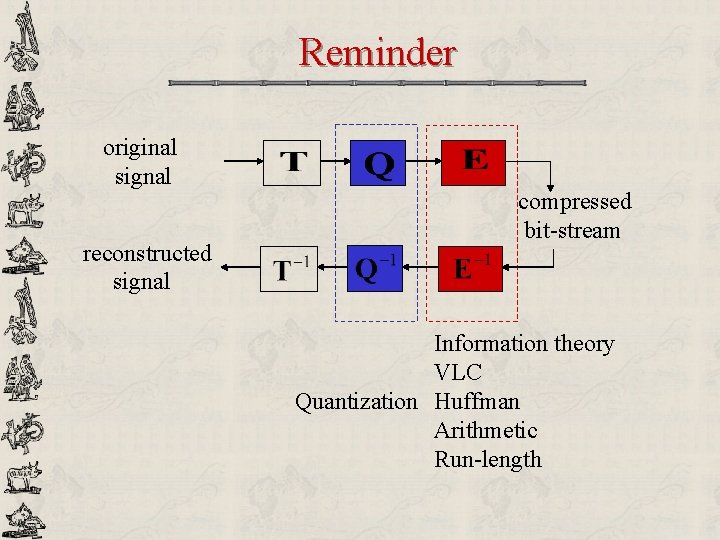
Reminder original signal reconstructed signal compressed bit-stream Information theory VLC Quantization Huffman Arithmetic Run-length

Quantization u Entropy coding techniques § Perform lossless coding § No flexibility or trade-off in bit-rate versus distortion u Quantization § Lossy non-linear mapping operation: a range of amplitude is mapped to a unique level or codeword § Approximation of a signal source using a finite collection of discrete amplitudes § Controls the rate-distortion trade-off § Applications § A/D conversion § Compression

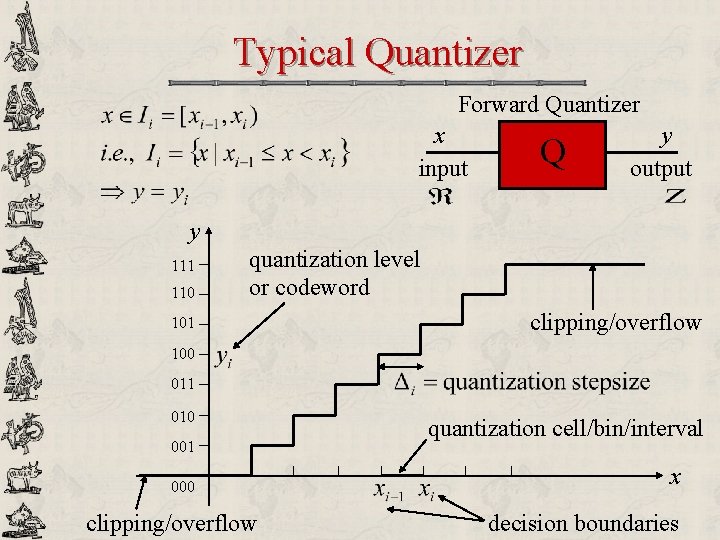
Typical Quantizer Forward Quantizer x input Q y output y 111 110 quantization level or codeword 101 clipping/overflow 100 011 010 001 000 clipping/overflow quantization cell/bin/interval x decision boundaries

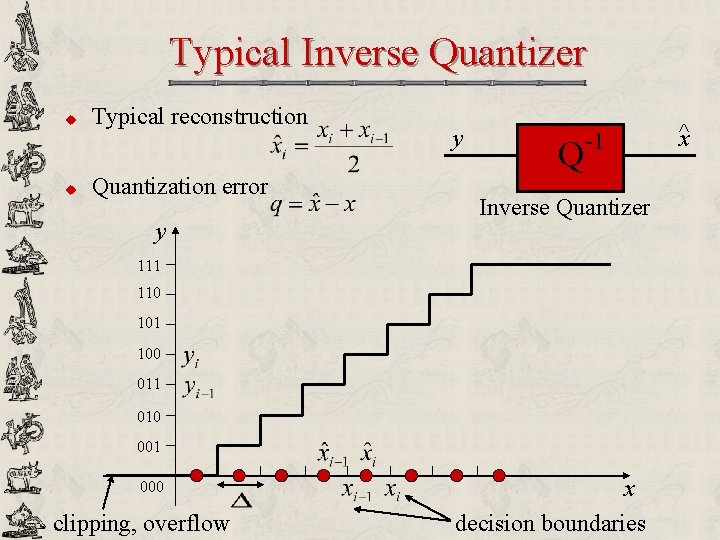
Typical Inverse Quantizer u u Typical reconstruction Quantization error y y Q -1 Inverse Quantizer 111 110 101 100 011 010 001 000 clipping, overflow x decision boundaries ^x

Mid-rise versus Mid-tread y y x Uniform Midrise Quantizer u u Popular in ADC For a b-bit midrise x Uniform Midtread Quantizer u u Popular in compression For a b-bit midtread

Quantization Errors u Approximation error § Lack of quantization resolution, too few quantization levels, too large quantization step-size § Causes staircase effect § Solution: increases the number of quantization levels, and hence, increase the bit-rate u Clipping error § Inadequate quantizer range limits, also known as overflow § Solution § Requires knowledge of the input signal § Typical practical range for a zero-mean signal

Quantization: Error Model x x Q Q + -1 u Assumptions: u Quantization error: u Mean-squared distortion measure: ^x x^

Quantization Error Variance x + would like to minimize ^x

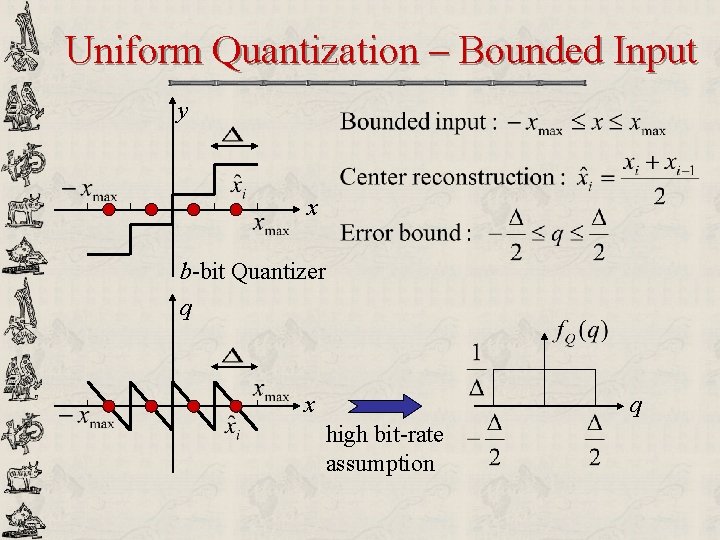
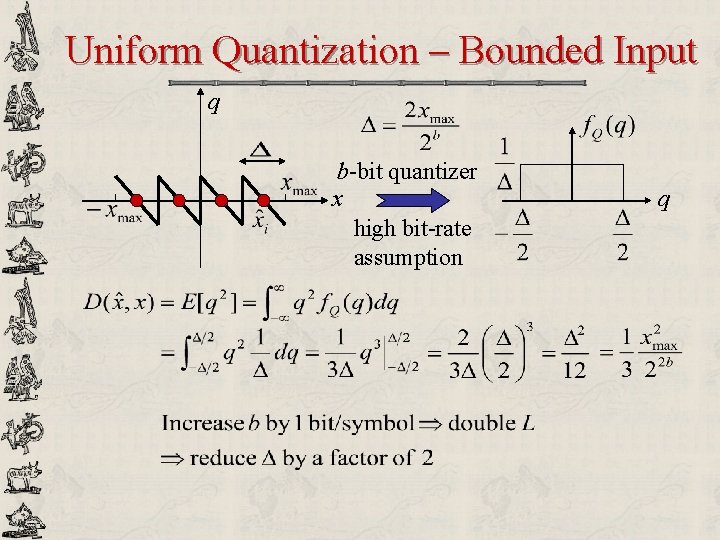
Uniform Quantization – Bounded Input y x b-bit Quantizer q x q high bit-rate assumption

Uniform Quantization – Bounded Input q b-bit quantizer x high bit-rate assumption q

Signal-to-Noise Ratio u Definition of SNR in decibel (d. B) power of the signal power of the noise u For quantization noise Suppose that we now add 1 more bit to our Q resolution:

Example Design a 3 -bit uniform quantizer for a signal with range [0, 128] u Maximum possible number of levels: u Quantization stepsize: u Quantization levels: u Reconstruction levels: u Maximum quantization error:

Example of Popular Quantization u Round u Floor u Ceiling y x Uniform midtread quantizer from Round and Floor

Quantization from Rounding y – 14 – 10 – 6 – 2 2 6 10 14 x Uniform Quantizer, step-size=4

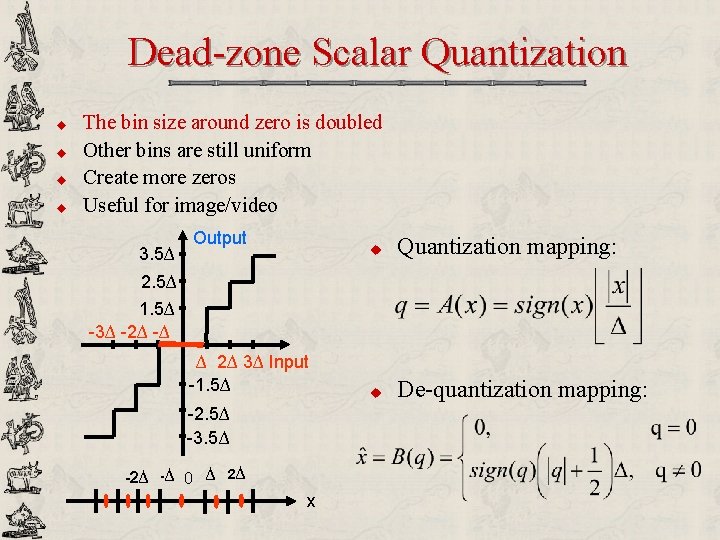
Dead-zone Scalar Quantization u u The bin size around zero is doubled Other bins are still uniform Create more zeros Useful for image/video 3. 5∆ Output u Quantization mapping: u De-quantization mapping: 2. 5∆ 1. 5∆ -3∆ -2∆ -∆ ∆ 2∆ 3∆ Input -1. 5∆ -2. 5∆ -3. 5∆ -2∆ -∆ 0 ∆ 2∆ x

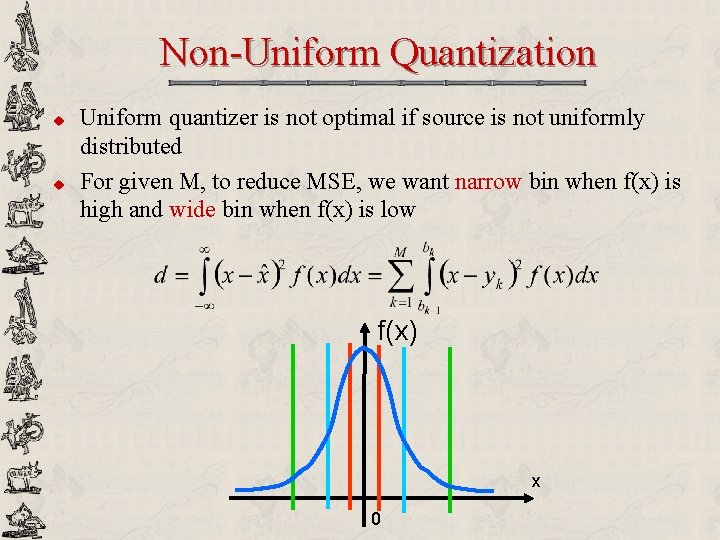
Non-Uniform Quantization u u Uniform quantizer is not optimal if source is not uniformly distributed For given M, to reduce MSE, we want narrow bin when f(x) is high and wide bin when f(x) is low f(x) x 0

Optimal Scalar Quantization u Problem Statement: u Optimal Encoder for a Given Decoder: u Notes: § Non-uniform quantizer under consideration § Reconstruction can be anywhere, not necessarily the center of the interval

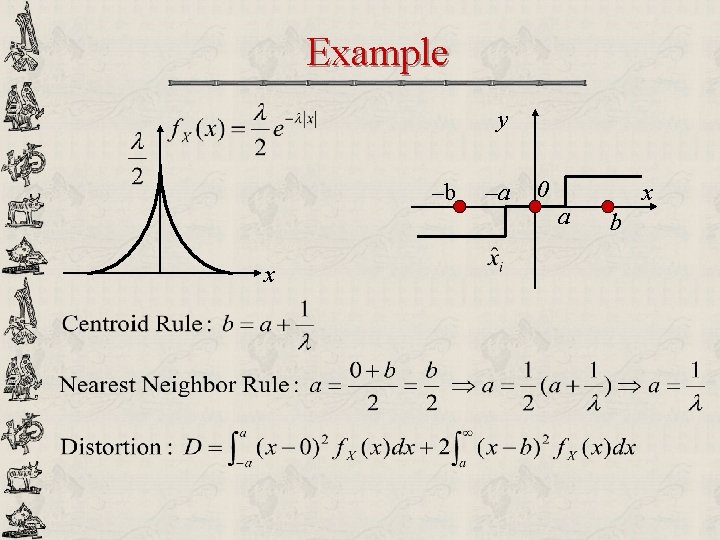
Optimal Scalar Quantization Fundamental Theorem of Calculus Nearest Neighbor Rule

Optimal Scalar Quantization u Optimal Decoder for a Given Encoder: Centroid Rule

Lloyd-Max Quantizer u u Main idea [Lloyd 1957] [Max 1960] § solving these 2 equation iteratively until D converges Input Codebook Nearest Neighbor Partitioning Centroid Computation index of m-th iteration u Assumptions § Input PDF is known and stationary § Entropy has not been taken into account Updated Codebook

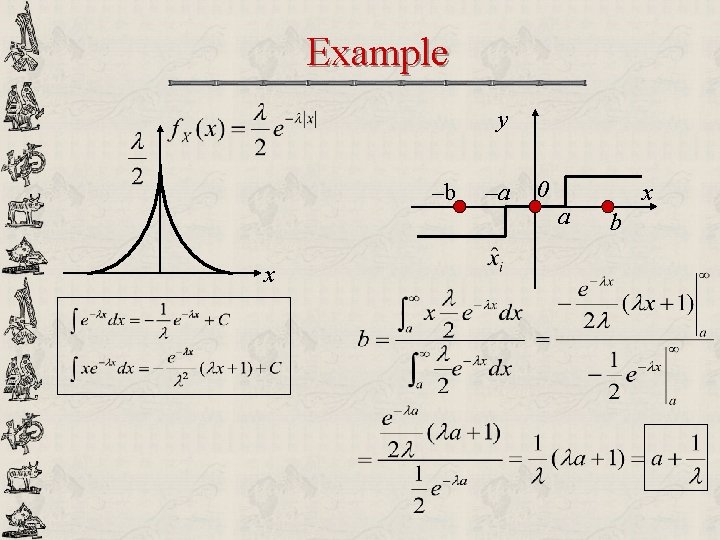
Example y –b x –a 0 a x b

Example y –b x –a 0 a x b

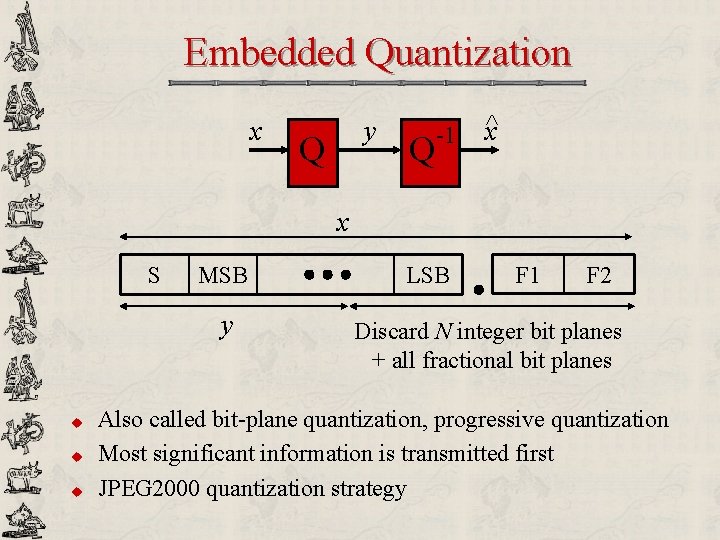
Embedded Quantization x y Q Q -1 ^x x S MSB y u u u LSB F 1 F 2 Discard N integer bit planes + all fractional bit planes Also called bit-plane quantization, progressive quantization Most significant information is transmitted first JPEG 2000 quantization strategy

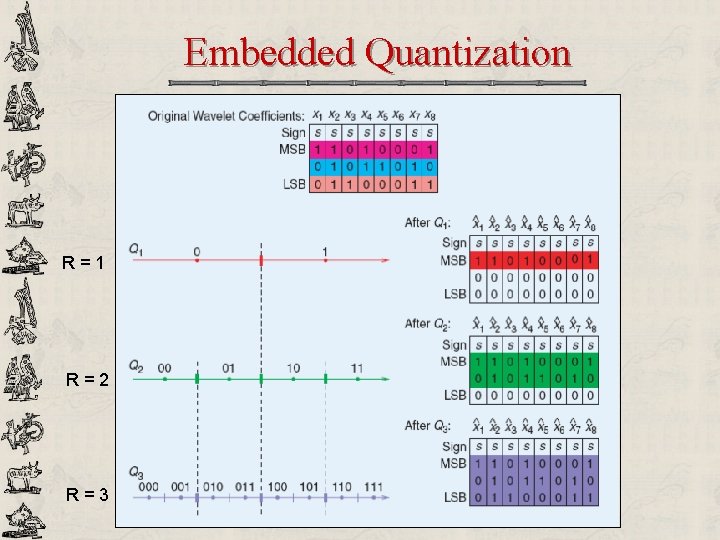
Embedded Quantization R=1 R=2 R=3

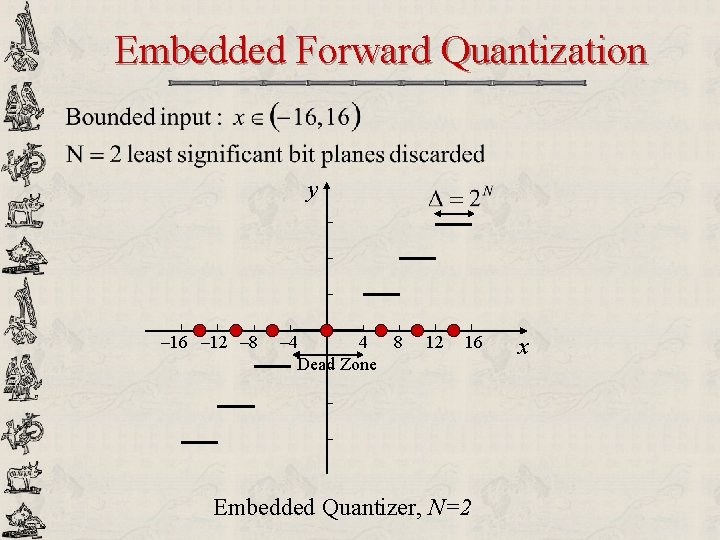
Embedded Forward Quantization y – 16 – 12 – 8 – 4 4 8 Dead Zone 12 16 Embedded Quantizer, N=2 x

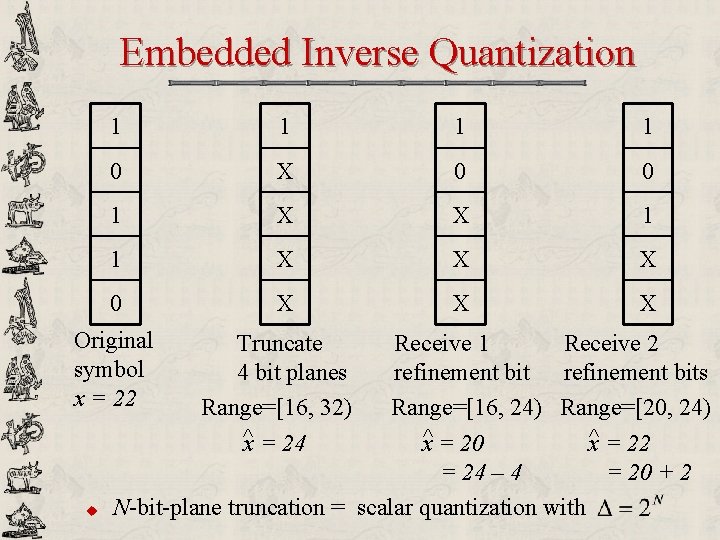
Embedded Inverse Quantization 1 1 0 X 0 0 1 X X 1 1 X X X 0 X X X Original symbol x = 22 u Truncate 4 bit planes Range=[16, 32) ^x = 24 Receive 1 Receive 2 refinement bits Range=[16, 24) Range=[20, 24) x^ = 20 x^ = 22 = 24 – 4 = 20 + 2 N-bit-plane truncation = scalar quantization with

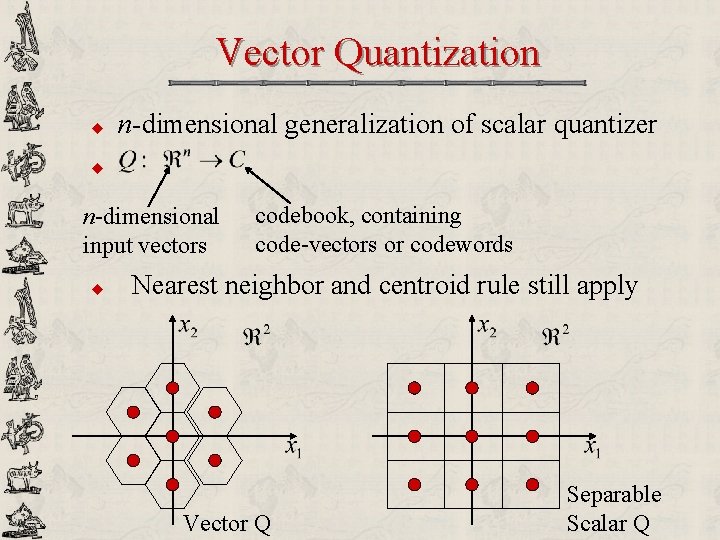
Vector Quantization u n-dimensional generalization of scalar quantizer u n-dimensional input vectors u codebook, containing code-vectors or codewords Nearest neighbor and centroid rule still apply Vector Q Separable Scalar Q