Quantities in Chemical Reactions Stoichiometry Quantities in Chemical

Quantities in Chemical Reactions: Stoichiometry

Quantities in Chemical Reactions • Balanced Chem Equation gives MOLE ratio • In a chemical reaction, amount of every substance used or made is related to the amounts of all the other substances üLaw of Conservation of Mass • Reaction Stoichiometry: the study of the numerical relationship between chemical quantities in a chemical reaction 2

Chapter Objectives • ***Use the balanced equation to solve mole-tomole and mass-to-mass stoichiometry problems • **Understand limiting reagent/reactant vs. excess reactant • Understand theoretical yield and percent yield 3

About Bunsen Burner Robert Bunsen: the Burner, the spectroscopy Recall how you would adjust the flame in a Bunsen Burner: • Small flame: more gas, more air • Yellow “fluffy”: more air • Noisy unsteady: less air 4 Conclusion: Chemical reaction follows certain ratio

Recipe: Making Pancakes • The number of pancakes you can make depends on the amount of the Ingredients you use 1 cup Flour + 2 Eggs + ½ tsp Baking Powder 5 Pancakes • Mathematically (as Conversion Factor) 1 cu flour 2 eggs ½ tsp baking powder 5 pancakes 5

More Pancakes? More Everything! 1 cu flour 2 eggs ½ tsp baking powder 5 pancakes Make more than 5 pancakes? • The number of eggs, and baking power too, determines the number of pancakes you can make Conversion Factor, again! Example: To make 20 pancakes, how many eggs we need? assuming you have enough everything else 20 pancakes x ----------- = eggs 6

Balanced Equation: Mole-to-Mole Conversions • Balanced equation = “recipe” for a chemical reaction, providing Conversion Factors for calculation. • Equation 3 H 2(g) + N 2(g) 2 NH 3(g) means: ___ molecules of H 2 react with ____ molecule of N 2, make ____ molecules of NH 3 or __ molecules H 2 __ molecule N 2 __ molecules NH 3 • since we count molecules by moles ___ moles H 2 ___ mole N 2 ___ moles NH 3 7

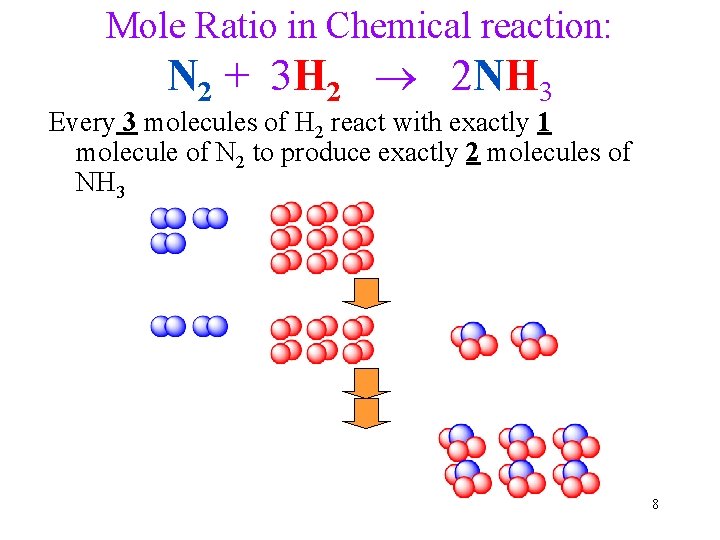
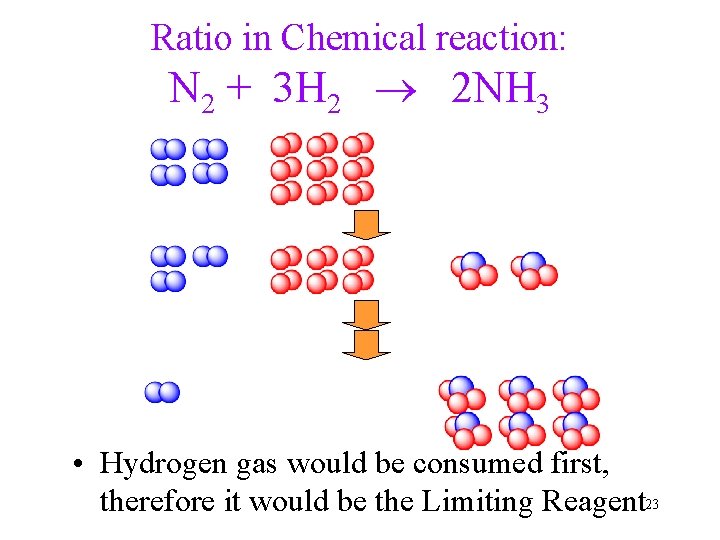
Mole Ratio in Chemical reaction: N 2 + 3 H 2 2 NH 3 Every 3 molecules of H 2 react with exactly 1 molecule of N 2 to produce exactly 2 molecules of NH 3 8

Example: Mole-to-Mole Conversions

Example: How many moles of H 2 O result from the complete combustion of 3. 4 mol of CH 4 in the reaction below? CH 4 + 2 O 2 CO 2 + 2 H 2 O • Write down the quantity to find and/or its units. Find: ? moles water • Collect Needed Conversion Factors: 1 mole CH 4 2 moles H 2 O • Start with non-Converion factor: 3. 4 mol CH 4 x ------------ = mol H 2 O 6. 8 moles H 2 O 10

Group Practice – For the following equation, find how many mole of 2 nd product will be produced when 1. 23 mole of 1 st reactant is consumed. 2 HBr(aq) + K 2 SO 3(aq) H 2 O(l) + SO 2(g) + 2 KBr(aq) 3 K 2 CO 3(aq) + 2(NH 4)3 PO 4(aq) 3(NH 4)2 CO 3(aq) + 2 K 3 PO 4(aq) Ba(OH)2(aq) + H 2 SO 4(aq) Ba. SO 4(s) + 2 H 2 O(l) Stoichiometry: http: //www. sciencegeek. net/Chemistry/taters/Unit 4 Stoichiometry. htm Stoichiometry: http: //www. lsua. us/chem 1001/stoichiometry. html 11 Tro: Chemistry: A Molecular Approach, 2/e 11

Stoichiometry: Mass-to-Mass Conversions • Relationship between Mass and Number of Moles of a chemical: Molar Mass 1 mole = Molar Mass in grams • Molar Mass of the chemicals in the reaction + Balanced chemical equation : convert from the Mass of any chemical in the reaction to the Mass of any other 12

Example: Mass-to-Mass Conversions Balanced equation: a. A + b. B c. C + d. D Mass A _____ A ____ B Mass B _____ B ____ D Mass D

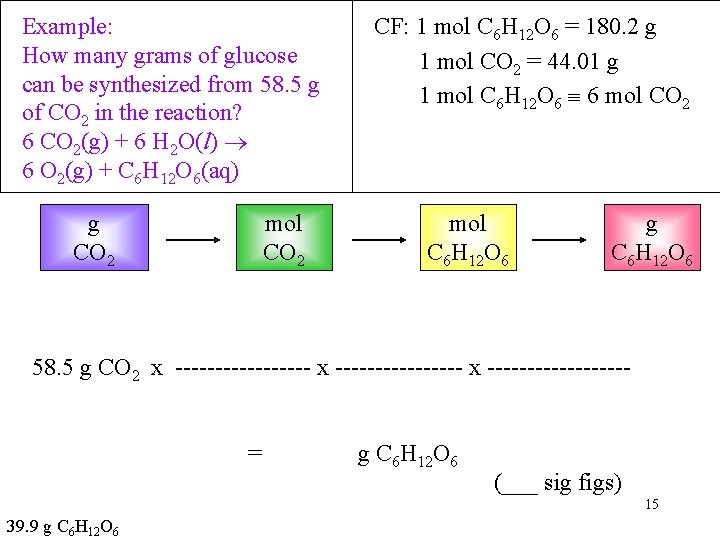
Example: How many grams of glucose (C 6 H 12 O 6) can be synthesized from 58. 5 g of CO 2 in the photosynthesis? 6 CO 2(g) + 6 H 2 O(l) 6 O 2(g) + C 6 H 12 O 6(aq) Information Given: 55. 4 g CO 2 Find: g C 6 H 12 O 6 • Collect Needed Conversion Factors: Molar Mass C 6 H 12 O 6 = 180. 2 g/mol Molar Mass CO 2 = 44. 01 g/mol From the equation: 1 mole C 6 H 12 O 6 ______ mol CO 2 14

Example: How many grams of glucose can be synthesized from 58. 5 g of CO 2 in the reaction? 6 CO 2(g) + 6 H 2 O(l) 6 O 2(g) + C 6 H 12 O 6(aq) g CO 2 mol CO 2 CF: 1 mol C 6 H 12 O 6 = 180. 2 g 1 mol CO 2 = 44. 01 g 1 mol C 6 H 12 O 6 6 mol CO 2 mol C 6 H 12 O 6 g C 6 H 12 O 6 58. 5 g CO 2 x -----------------= g C 6 H 12 O 6 (___ sig figs) 15 39. 9 g C 6 H 12 O 6

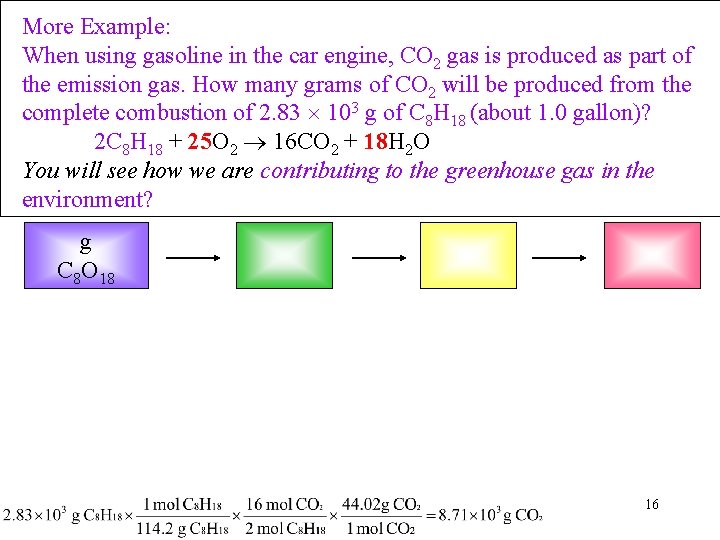
More Example: When using gasoline in the car engine, CO 2 gas is produced as part of the emission gas. How many grams of CO 2 will be produced from the complete combustion of 2. 83 103 g of C 8 H 18 (about 1. 0 gallon)? 2 C 8 H 18 + 25 O 2 16 CO 2 + 18 H 2 O You will see how we are contributing to the greenhouse gas in the environment? g C 8 O 18 16

Group Practice – For the following equation, how many grams of 2 nd product can be produced when 1. 23 g of 1 st reactant is consumed? 2 HBr(aq) + K 2 SO 3(aq) H 2 O(l) + SO 2(g) + 2 KBr(aq) 3 K 2 CO 3(aq) + 2(NH 4)3 PO 4(aq) 3(NH 4)2 CO 3(aq) + 2 K 3 PO 4(aq) Ba(OH)2(aq) + H 2 SO 4(aq) Ba. SO 4(s) + 2 H 2 O(l) Stoichiometry: http: //www. sciencegeek. net/Chemistry/taters/Unit 4 Stoichiometry. htm Stoichiometry: http: //www. lsua. us/chem 1001/stoichiometry. html 17 Tro: Chemistry: A Molecular Approach, 2/e 17

Making Pancakes: What if …. ? • Same receipe: 1 cup Flour + 2 Eggs + ½ tsp Baking Powder 5 Pancakes • How many pancakes we can make if we had 3 cups of flour, 10 eggs, and 4 tsp of baking powder? 18

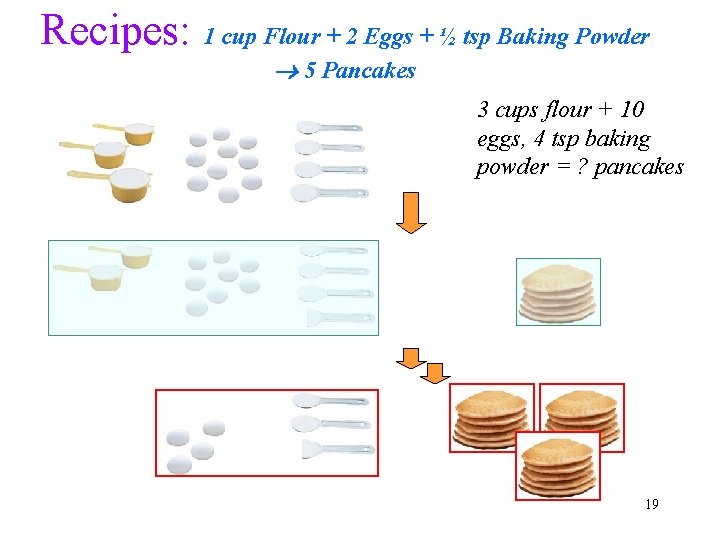
Recipes: 1 cup Flour + 2 Eggs + ½ tsp Baking Powder 5 Pancakes 3 cups flour + 10 eggs, 4 tsp baking powder = ? pancakes 19

Given certain amount of each ingredient, The actual number of pancakes is the ______ amount of pancakes as calculated below. 3 cups flour + 10 eggs, 4 tsp baking powder let’s find out #pancakes from each ingredient: 20

What we learned from making pancakes? • Each ingredient could potentially make a different number of pancakes • but all the ingredients have to work together, following the right ratio! • The maximal amount of pancakes depends on the ingredient that gives the least amount of pancakes. Here as flour àOnce we make 15 pancakes, the flour runs out, no more pancakes can be made! 21

From making pancakes to Chemical Reaction • According to the balanced equation, all the reactants have to work together, following the right MOLE ratio! • The amount of products depends on the reactant that runs out the first, since if one reactant runs out, no more products can be made. • The reactant that rans out the first is the Limiting Reactant (also known as “Limiting Reagent”) 22

Ratio in Chemical reaction: N 2 + 3 H 2 2 NH 3 • Hydrogen gas would be consumed first, therefore it would be the Limiting Reagent 23

How to find the Limiting Reactant (L. R. ) When the amount of all reactants are given (either as MOLE or as Mass), the actual amount of products depends on the L. R. • To find the L. R. , calculate the amount of ONE product from each reactant (assuming there are enough OTHER reactants) • The REACTANT that gives the LEAST amount of product is the L. R. • Theoretical yield: The maximum amount of products we can make from the reaction. It depends on the limiting reactant. 24

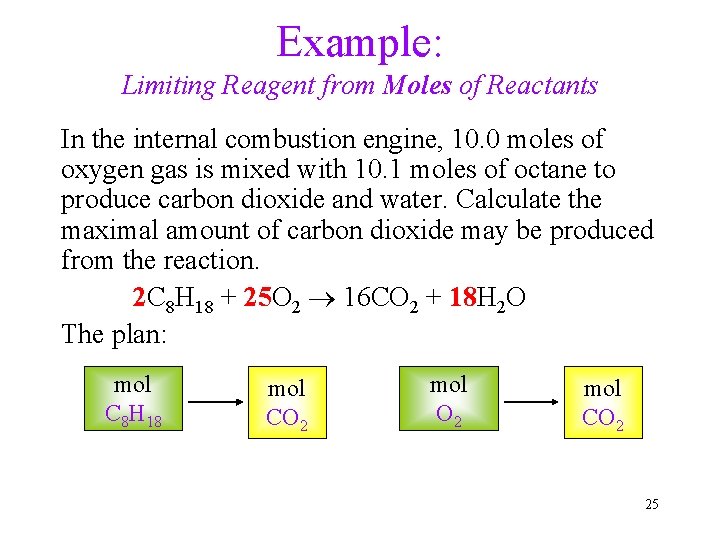
Example: Limiting Reagent from Moles of Reactants In the internal combustion engine, 10. 0 moles of oxygen gas is mixed with 10. 1 moles of octane to produce carbon dioxide and water. Calculate the maximal amount of carbon dioxide may be produced from the reaction. 2 C 8 H 18 + 25 O 2 16 CO 2 + 18 H 2 O The plan: mol C 8 H 18 mol CO 2 25

In the internal combustion engine, 10. 0 moles of oxygen gas is mixed with 10. 1 moles of octane to produce carbon dioxide and water. The reaction is as follows: 2 C 8 H 18 + 25 O 2 16 CO 2 + 18 H 2 O Calculate the maximal amount of carbon dioxide may be produced from the reaction. 10. 1 mol C 8 H 18 x -------- = _____ mol CO 2 10. 0 mol O 2 x -------- = _____ mol CO 2 From octane: 80. 8 mol. Answer: 6. 40 mol CO 2 From oxygen, 6. 40 mol. Oxygen as L. R. 26

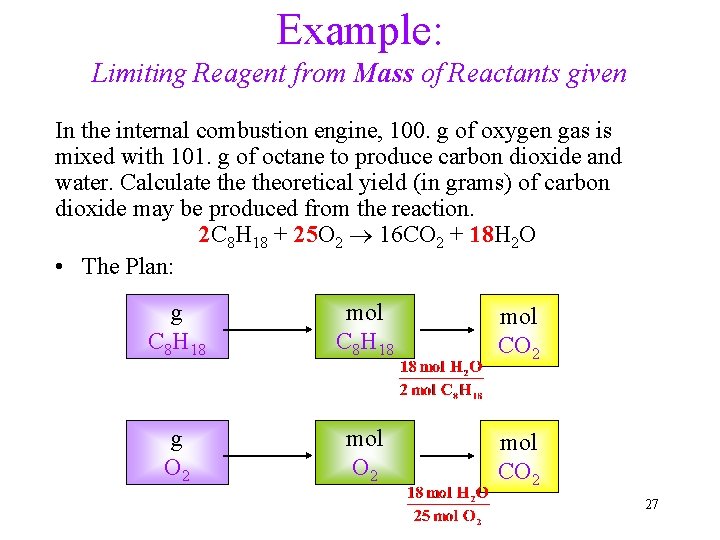
Example: Limiting Reagent from Mass of Reactants given In the internal combustion engine, 100. g of oxygen gas is mixed with 101. g of octane to produce carbon dioxide and water. Calculate theoretical yield (in grams) of carbon dioxide may be produced from the reaction. 2 C 8 H 18 + 25 O 2 16 CO 2 + 18 H 2 O • The Plan: g C 8 H 18 mol CO 2 g O 2 mol CO 2 27

In the internal combustion engine, 100. g of oxygen gas is mixed with 101. g of octane to produce carbon dioxide and water: 2 C 8 H 18 + 25 O 2 16 CO 2 + 18 H 2 O Calculate theoretical yield (in grams) of carbon dioxide from the reaction. Oxygen as L. R. 2. 00 mol CO 2. Answer: 88. 0 g CO 2 28

Group Practice: Limiting Reactant A. when 1. 23 g each of reactant are mixed, calculate theoretical yield (in grams) of 2 nd product. B. Which reagent is in excess? 2 HBr(aq) + K 2 SO 3(aq) H 2 O(l) + SO 2(g) + 2 KBr(aq) 3 K 2 CO 3(aq) + 2(NH 4)3 PO 4(aq) 3(NH 4)2 CO 3(aq) + 2 K 3 PO 4(aq) Ba(OH)2(aq) + H 2 SO 4(aq) Ba. SO 4(s) + 2 H 2 O(l) 29 29

Actual Yield vs. Percent Yield Actual yield: The actual amount of product made in a chemical reaction (due to Controllable/Uncontrollable factors that results in less product. Such as during making pancakes, spill some of the batter, burn a pancake, drop one on the floor or else so that finally 11 pancakes are made out of 15. • Actual yield can NOT be calculated, only from experiment. • Percent yield : the efficiency of production during chemical reactions. 30

Theoretical and Actual Yield To determine theoretical yield, • Use reaction stoichiometry to determine the amount of product EACH reactants could make. • The theoretical yield will always be the least possible amount of product. ü The theoretical yield will always come from the _______ reactant. • Because of both controllable and uncontrollable factors, Actual yield < Theoretical yield, so percent yield is no more than 100%. 31

In the internal combustion engine, 100. g of oxygen gas is mixed with 101. g of octane to produce carbon dioxide and water: 2 C 8 H 18 + 25 O 2 16 CO 2 + 18 H 2 O If 80. 0 g carbon dioxide is actually produced in the reaction, calculate the percent yield of carbon dioxide. Oxygen as L. R. 2. 00 mol CO 2. Theoretical yield: 88. 0 g CO 2 32

Example: Most people believe that exercise helps “burning” carbohydrates and prevents weight gain. When a person drinks two cans of soda (100. 0 g of sugar, C 12 H 22 O 11) per day. Meanwhile, he didn’t work out, neither did he eat any other carbohydrates, nor protein or fat. Measurement showed he released 144. 0 g CO 2 during this day through this reaction: C 12 H 22 O 11 + 12 O 2 12 CO 2 + 11 H 2 O Question: • What is the Theoretical Yield of CO 2 from complete “burning sugar” in his body? • How much of the sugar was “burned” into CO 2? • What is the Percent Yield of CO 2? 33

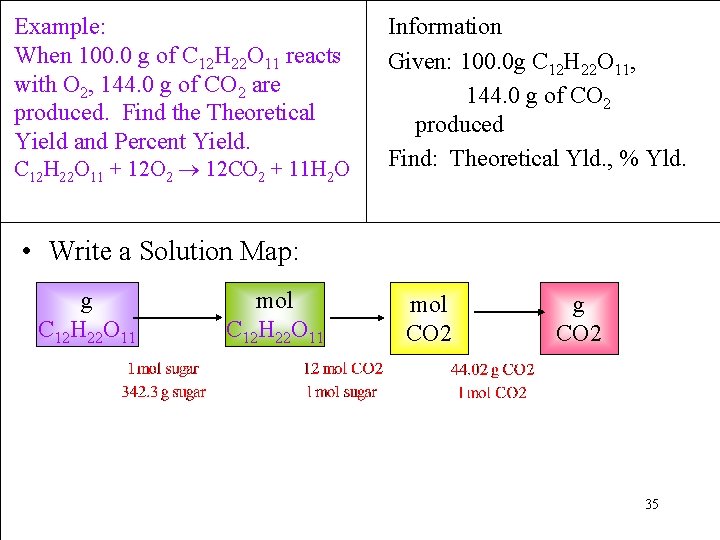
Example: When 100. 0 g of C 12 H 22 O 11 reacts with O 2, 144. 0 g of CO 2 are produced. Find the Theoretical Yield and Percent Yield. Information Given: 100. 0 g C 12 H 22 O 11, 144. 0 g of CO 2 produced Find: Theor. Yld. , % Yld. C 12 H 22 O 11 + 12 O 2 12 CO 2 + 11 H 2 O • Collect Needed Conversion Factors: Molar Mass C 12 H 22 O 11 = 342. 4 g/mol Molar Mass CO 2 = 44. 02 g/mol 1 mole C 12 H 22 O 11 12 mol CO 2 (from the chem. equation) 34

Example: When 100. 0 g of C 12 H 22 O 11 reacts with O 2, 144. 0 g of CO 2 are produced. Find the Theoretical Yield and Percent Yield. C 12 H 22 O 11 + 12 O 2 12 CO 2 + 11 H 2 O Information Given: 100. 0 g C 12 H 22 O 11, 144. 0 g of CO 2 produced Find: Theoretical Yld. , % Yld. • Write a Solution Map: g C 12 H 22 O 11 mol CO 2 g CO 2 35

Example: When 100. 0 g of C 12 H 22 O 11 reacts with O 2, 144. 0 g of CO 2 are produced. Find the Theoretical Yield and Percent Yield. C 12 H 22 O 11 + 12 O 2 12 CO 2 + 11 H 2 O Apply the Solution Map: • Theoretical yield of CO 2 (“total burn out of carbs”) • Percent yield = 144. 0 g/154. 3 g x 100% = 93. 32% 36

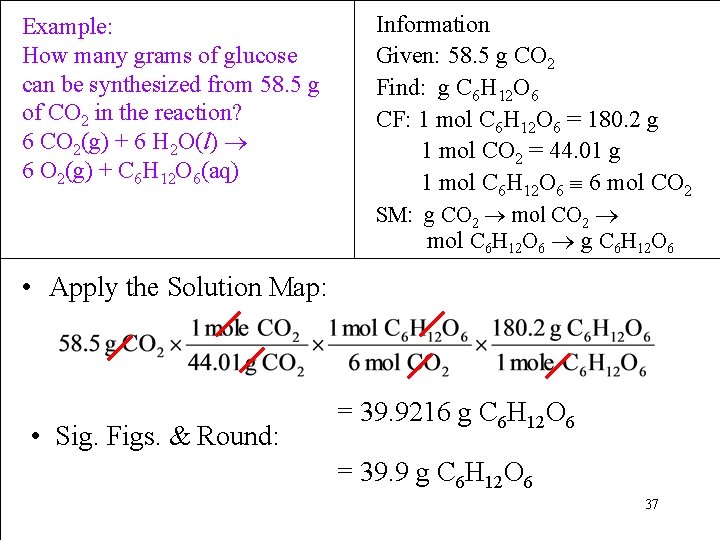
Example: How many grams of glucose can be synthesized from 58. 5 g of CO 2 in the reaction? 6 CO 2(g) + 6 H 2 O(l) 6 O 2(g) + C 6 H 12 O 6(aq) Information Given: 58. 5 g CO 2 Find: g C 6 H 12 O 6 CF: 1 mol C 6 H 12 O 6 = 180. 2 g 1 mol CO 2 = 44. 01 g 1 mol C 6 H 12 O 6 6 mol CO 2 SM: g CO 2 mol C 6 H 12 O 6 g C 6 H 12 O 6 • Apply the Solution Map: • Sig. Figs. & Round: = 39. 9216 g C 6 H 12 O 6 = 39. 9 g C 6 H 12 O 6 37

How to find the Limiting Reactant (L. R. ): An alternative method • Starting from the mole of 1 st reactant in the equation, calculate the mole of 2 nd reactant required for complete reaction (use mole ratio); ü If calculated mol 2 nd reactant is smaller than actual (given), 2 nd reactant is more than enough, thus 1 st reactant is L. R. ; ü If calculated mol 2 nd reactant is larger than given, 2 nd reactant is not enough, thus 2 nd reactant is L. R. • If more than two reactants in the equation, decide “L. R. ” (pseudo. LR) between 1 st and 2 nd reactants first; then compare pseudo. LR with 3 rd reactant. • If pseudo. LR is the 38