Quantitative Research in Education Sohee Kang Ph D

Quantitative Research in Education Sohee Kang Ph. D. , lecturer Math and Statistics Learning Centre

Outline • Analyzing Educational Research Data • Collecting data • Using R (R commander) for describing and testing hypotheses

Analyzing Research Data • Example: a high school research team was interested in increasing student achievement by implementing a study skills program. • The first thing this team did was develop a survey, which all students completed. • Representing data made it quite easy to see what study skills students were already using and which ones they would like to learn more about.

Collecting Data • Observational Data Ex) survey data • Design of Experiments Ex) Classroom experiments

Let’s look at Survey questionnaire • Census at School Canada • Website link: http: //www. censusatschool. ca/

Census at School – Canada Questionnaire – Grades 9 to 12 2010/201 (selected questions)

Random Data Selector • • http: //rds. censusatschool. org. uk/ Country: Canada Email: ex)spollanen@gmail. com School/institution: University of Toronto Scarborough • Type the number on the screen

Select a sample size = 200

Which software to use to analyze data? R is a language and environment for statistical computing and graphics. R can be used for: data manipulation, data analysis, creating graphs, designing and running computer simulations.

Why R? • R is FREE: As an open-source project, you can use R free of charge. • R is POWERFUL: Leading academics and researches from around the world use R to develop the latest methods in statistics, machine learning, and predictive modeling.

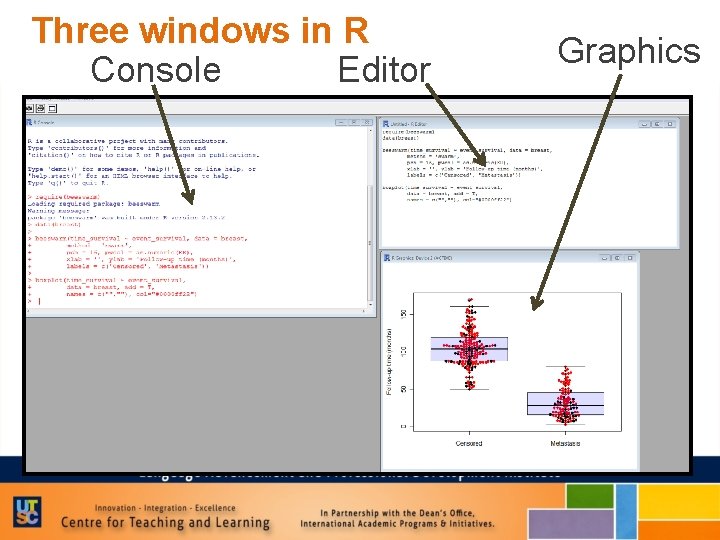
Three windows in R Console Editor Graphics

Writing in R is like writing in English Jump three times forward Action Modifiers

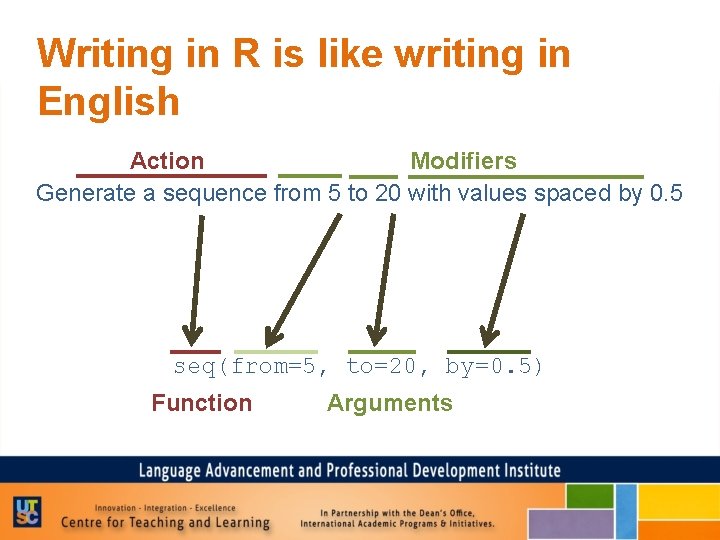
Writing in R is like writing in English Generate a sequence from 5 to 20 with values spaced by 0. 5 Action Modifiers

Writing in R is like writing in English Action Modifiers Generate a sequence from 5 to 20 with values spaced by 0. 5 seq(from=5, to=20, by=0. 5) Function Arguments

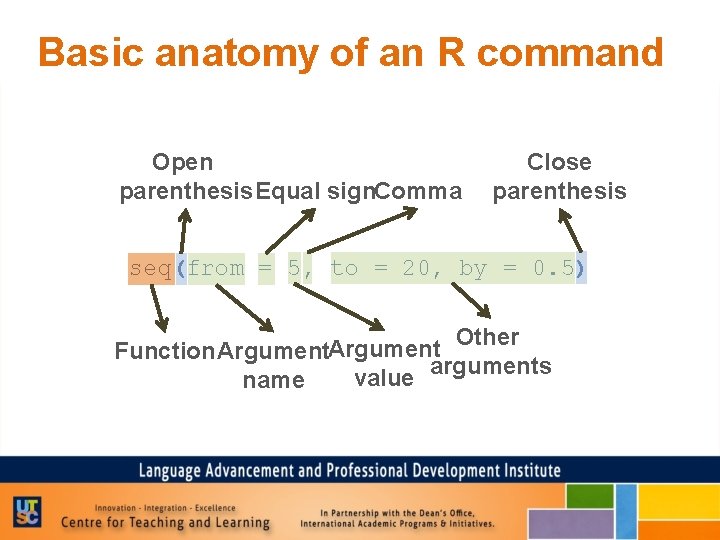
Basic anatomy of an R command Open parenthesis Equal sign. Comma Close parenthesis seq(from = 5, to = 20, by = 0. 5) Other Function Argument value arguments name

Writing R code: 1. Read a downloaded file 2. Choose the selected Variables: Province, Gender, Language, Height, Physical Days, Smoke, Favorite Subject, Pressure, Travel, Communication

Descriptive Statistics • Categorical Variables: Province, Gender, Favorite Subject, Travel, Pressure, Communication • Quantitative Variables: Language, Height, Physical Days, Smoke

Graphs • For Categorical variables: Bar plot and Pie chart • For Quantitative variables: Histogram and boxplot

Summary Statistics • For Categorical variables: Frequency, relative frequency • For Quantitative variables: Mean, Median, SD (Standard deviation)

Relationship between Two Variables • Categorical vs Categorical: Contingency Tables • Categorical vs Quantitative: Tables of Statistics (side by side boxplot) • Quantitative vs Quantitative Correlation (Scatter plot)

Pre-Post Test: Paired T-test • Research question type: Difference between two related (paired or matched) variables. • What kind of variables? Quantitative (Continuous) • Common Applications: Comparing the means of data from two related samples; say, observations before and after an intervention on the same participant.

Example: Research question: Is there a difference in mark following a teaching intervention? Example Data Student Before Mark 1 18 2 21 3 16 4 22 5 19 6 24 7 17 8 21 9 23 10 18 11 14 12 16 13 16 14 19 15 18 16 20 17 12 18 22 19 15 After Mark 22 25 17 24 16 29 20 23 19 20 15 15 18 26 18 24 18 25 19 20 16 17

Hypotheses: • Null hypothesis H 0: There is no difference in mean pre-post marks • Alternative hypothesis Ha: There is a difference in mean pre-post marks

Steps in R • Create a data file, “pre-post. txt” • Read data from R • Statistics > Means > Paired t-test data: prepost$Aftermark and prepost$Beforemark t = 3. 2313, df = 19, p-value = 0. 004395 alternative hypothesis: true difference in means is not equal to 0 95 percent confidence interval: 0. 7221251 3. 3778749 sample estimates: mean of the differences 2. 05

Results: • t test statistic value is t=3. 2313 and p-value is 0. 0004; there is very small probability to observe this t-test statistic value or more extreme values under the assumption that there is no mean difference. • Conclusion: There is a statistically significant, strong evidence that teaching intervention improved marks.