Quantitative phase estimation with a bright field microscope

Quantitative phase estimation with a bright field microscope Sri Rama Prasanna Pavani, Ariel Libertun, Sharon King, and Carol Cogswell Micro Optical – Imaging Systems Laboratory, ECE, University of Colorado at Boulder http: //moisl. colorado. edu Pavani et al - Univ. of Colorado, Boulder Frontiers in Optics 1 9/18/2007

Phase imaging – What? How? q q Transparent (phase) objects modulate only the phase of light Convert phase modulations into detectable intensity modulations Bright field X No quantitative phase Phase contrast DIC Digital Holography ü Quantitative phase for weak phase objects after reconstruction ü Quantitative phase after reconstruction ü No phase wrapping ü Thick phase objects X Halo and shading-off X Polarization sensitive ü Single image X Only for thin objects X Vibration sensitive X Multiple images X Phase wrapping Pavani et al - Univ. of Colorado, Boulder 2

Our method n Amplitude mask in the field diaphragm n Pattern is imaged on the sample n Phase object distorts the pattern n Record the distorted pattern n Vs 0. 2 (mm) 0. 1 0. 4 0 (m. 2 m) Analytical formula calculates phase Pavani et al - Univ. of Colorado, Boulder 0 0. 4 ) mm 0. 2 ( 3

Our method – 1 D No rm a l o Analytically relate deformation to the optical path length Tan gen t n 2 o Consider a 1 D phase object p(x) o Ray R from point A, after refraction, appears as if it originated from B o Deformation t(x) is the distance between A and B n 1 A t(x) B Pavani et al, “Quantitative structured-illumination phase microscopy”, submitted to Applied Optics, June 07 4 Pavani et al - Univ. of Colorado, Boulder. CMB 4, COSI 2007 Pavani et al, “Structured-illumination quantitative phase microscopy”,

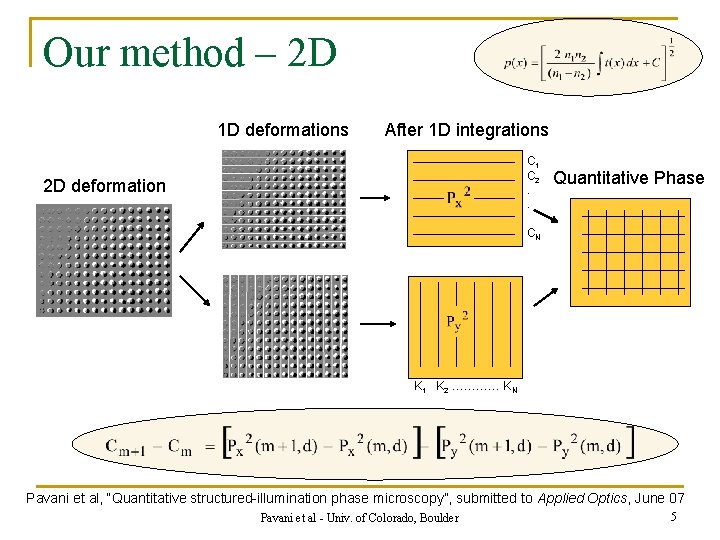
Our method – 2 D 1 D deformations After 1 D integrations C 1 C 2. . 2 D deformation Quantitative Phase CN K 1 K 2 ………… KN Pavani et al, “Quantitative structured-illumination phase microscopy”, submitted to Applied Optics, June 07 Pavani et al - Univ. of Colorado, Boulder 5

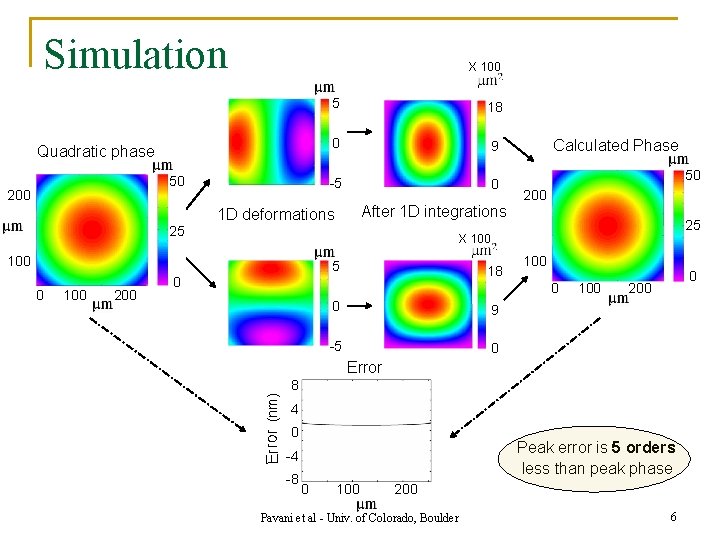
Simulation X 100 Quadratic phase 50 200 5 18 0 9 -5 0 After 1 D integrations 1 D deformations 25 5 200 18 0 200 25 100 0 0 9 -5 0 100 0 200 Error 8 Error (nm) 100 50 X 100 0 Calculated Phase 4 0 Peak error is 5 orders less than peak phase -4 -8 0 100 200 Pavani et al - Univ. of Colorado, Boulder 6

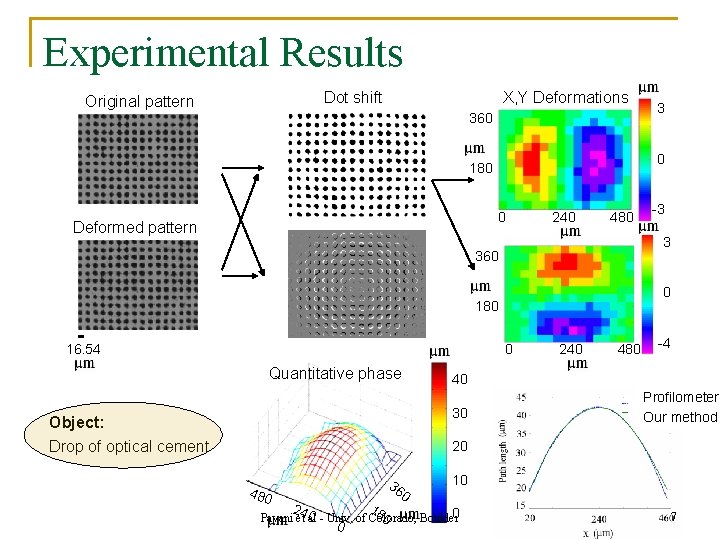
Experimental Results Dot shift Original pattern X, Y Deformations 360 0 180 0 Deformed pattern 240 480 0 180 0 Quantitative phase 240 480 -4 40 30 Object: Drop of optical cement -3 3 360 16. 54 3 Profilometer Our method 20 480 36 1 2 0 10 80 0 Pavani et 40 al - Univ. of Colorado, Boulder 0 7

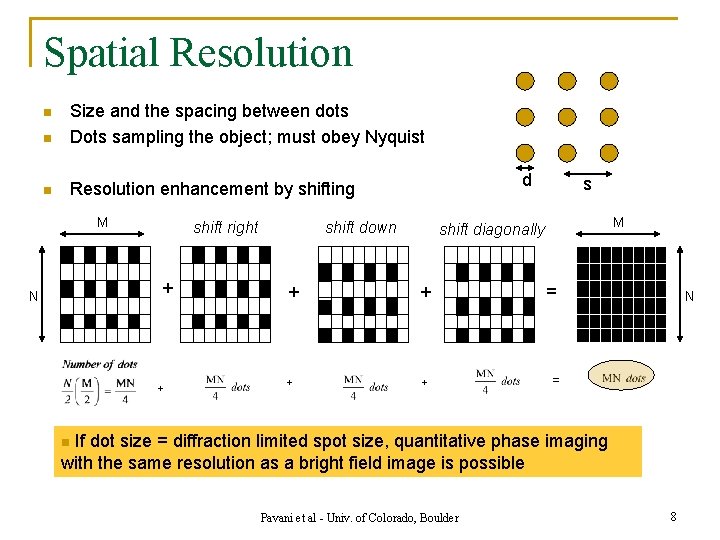
Spatial Resolution n Size and the spacing between dots Dots sampling the object; must obey Nyquist n Resolution enhancement by shifting n M shift right + N + d shift down s M shift diagonally + + = N If dot size = diffraction limited spot size, quantitative phase imaging with the same resolution as a bright field image is possible n Pavani et al - Univ. of Colorado, Boulder 8

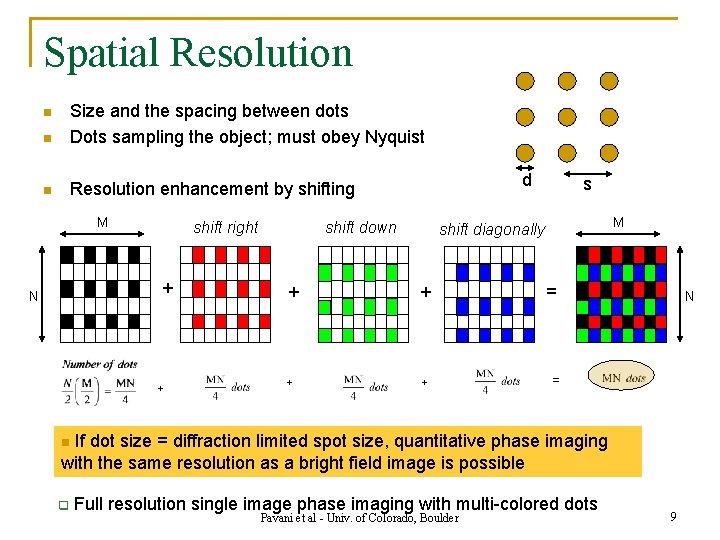
Spatial Resolution n Size and the spacing between dots Dots sampling the object; must obey Nyquist n Resolution enhancement by shifting n M shift right + N + d shift down s M shift diagonally + + = N If dot size = diffraction limited spot size, quantitative phase imaging with the same resolution as a bright field image is possible n q Full resolution single image phase imaging with multi-colored dots Pavani et al - Univ. of Colorado, Boulder 9

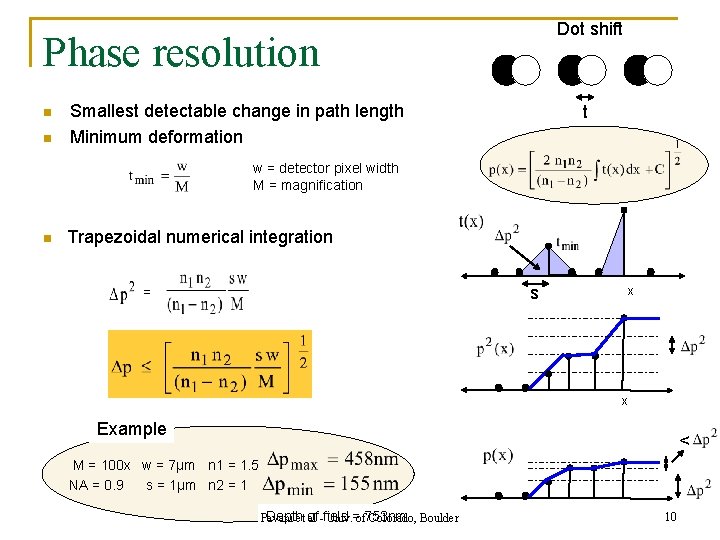
Dot shift Phase resolution n n Smallest detectable change in path length Minimum deformation t w = detector pixel width M = magnification n Trapezoidal numerical integration s = x x Example < M = 100 x w = 7µm n 1 = 1. 5 NA = 0. 9 s = 1µm n 2 = 1 Depth Pavani et of al -field Univ. =of 753 nm Colorado, Boulder 10

Conclusion q Described wide field, full resolution quantitative phase imaging in a bright field microscope q Phase is calculated from deformation using an analytical formula q Conservative calculations with a 100 x objective predict a phase resolution of 155 nm Pavani et al - Univ. of Colorado, Boulder 11

Acknowledgements n n n Prof. Rafael Piestun Prof. Gregory Beylkin Vaibhav Khire CDMOptics Ph. D Fellowship National Science Foundation Grant No. 0455408 Pavani et al - Univ. of Colorado, Boulder 12

References n J. W. Goodman, Introduction to Fourier Optics, (Roberts & Company, 2005) n M Pluta, Advanced Light Microscopy, vol 2: Specialised Methods, (Elsevier, 1989) n M. R. Arnison, K. G. Larkin, C. J. R. Sheppard, N. I. Smith, C. J. Cogswell, “Linear phase imaging using differential interference contrast microscopy” Journal of Microscopy 214 (1), 7– 12 (2004) n C. Preza, "Rotational-diversity phase estimation from differential-interference-contrast microscopy images, " J. Opt. Soc. Am. A 17, 415 -424 (2000) n Sharon V. King, Ariel R. Libertun, Chrysanthe Preza, and Carol J. Cogswell, “Calibration of a phase-shifting DIC microscope for quantitative phase imaging, ” Proc. SPIE 6443, 64430 M (2007) n E. Cuche, F. Bevilacqua, and C. Depeursinge, “Digital holography for quantitative phase-contrast imaging, ” Opt. Lett. 24, 291 -293 (1999) n P. Marquet, B. Rappaz, P. J. Magistretti, E. Cuche, Y. Emery, T. Colomb, and C. Depeursinge, “Digital holographic microscopy: a noninvasive contrast imaging technique allowing quantitative visualization of living cells with subwavelength axial accuracy, ” Opt. Lett. 30, 468 -470 (2005) n M. Born and E. Wolf, Principles of Optics, ed. 7, (Cambridge University Press, Cambridge, U. K. , 1999). n A. C. Kak, M. Slaney, Principles of Computerized Tomographic Imaging, (IEEE Press, New York, NY, 1988) n A. C. Sullivan, Department of Physics, University of Colorado, Campus Box 390, Boulder, CO 80309, USA and R. Mc. Leod are preparing a manuscript to be called “Tomographic reconstruction of weak index structures in volume photopolymers. ” n Huang D, Swanson EA, Lin CP, Schuman JS, Stinson WG, Chang W, Hee MR, Flotte T, Gregory K, Puliafito CA, et al. , “Optical coherence tomography, ” Science 1991 Nov 22; 254(5035): 1178 -81. n A. F. Fercher, C. K. Hitzenberger, “Optical coherence tomography, ” Chapter 4 in Progress in Optics 44, Elsevier Science B. V. (2002) n A. F. Fercher, W. Drexler, C. K. Hitzenberger and T. Lasser, “Optical coherence tomography - principles and applications, ” Rep. Prog. Phys. 66 239– 303 (2003) n M. R. Ayres and R. R. Mc. Leod, "Scanning transmission microscopy using a position-sensitive detector, " Appl. Opt. 45, 8410 -8418 (2006) n Barone-Nugent, E. , Barty, A. & Nugent, K. “Quantitative phase-amplitude microscopy I: optical microscopy, ” J. Microsc. 206, 194– 203 (2002). n J. Hartmann, "Bemerkungen uber den Bau und die Justirung von Spektrographen, " Z. Instrumentenkd. 20, 47 (1900). n I. Ghozeil, “Hartmann and other screen tests, ” in Optical Shop Testing, D. Malacara, second edition Wiley, New York, 1992, pp. 367– 396. n R. V. Shack and B. C. Platt, “Production and use of a lenticular Hartmann screen, ” J. Opt. Soc. Am. 61, 656 (1971). n V. Srinivasan, H. C. Liu, and M. Halioua, “Automated phase-measuring profilometry of 3 -D diffuse objects, ” Appl. Opt. 23, 3105 - (1984) n M. G. L. Gustafsson, “Surpassing the lateral resolution limit by a factor of two using structured illumination microscopy, ” Journal of Microscopy 198 (2), 82– 87 (2000) n M. D. Feit and J. A. , J. Fleck, "Light propagation in graded-index optical fibers (T), " Appl. Opt. 17, 3990 - (1978) n Haralick, Robert M. , and Linda G. Shapiro. Computer and Robot Vision, Volume I. Addison-Wesley, 1992. pp. 28 -48. Pavani et al - Univ. of Colorado, Boulder 13

Applications and Future work n Industrial inspection, biological imaging n Extracting information from axial deformation n Extending the depth of field of the system n Fabrication of an amplitude mask with higher spatial resolution Pavani et al - Univ. of Colorado, Boulder 14

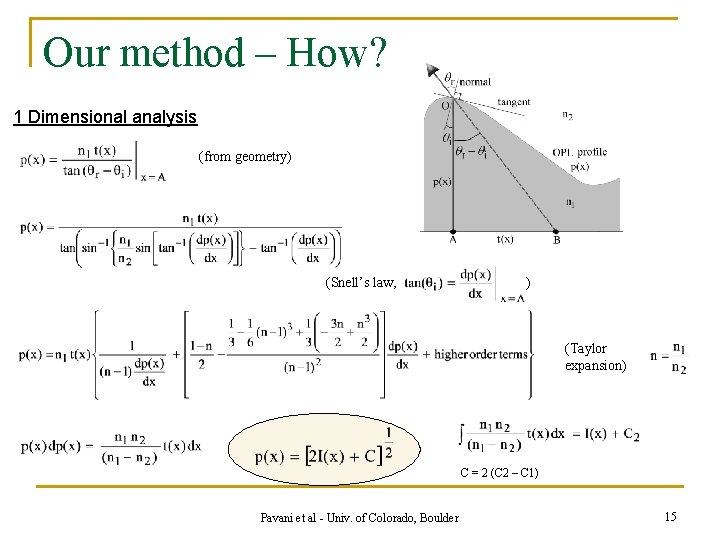
Our method – How? 1 Dimensional analysis (from geometry) (Snell’s law, ) (Taylor expansion) C = 2 (C 2 – C 1) Pavani et al - Univ. of Colorado, Boulder 15

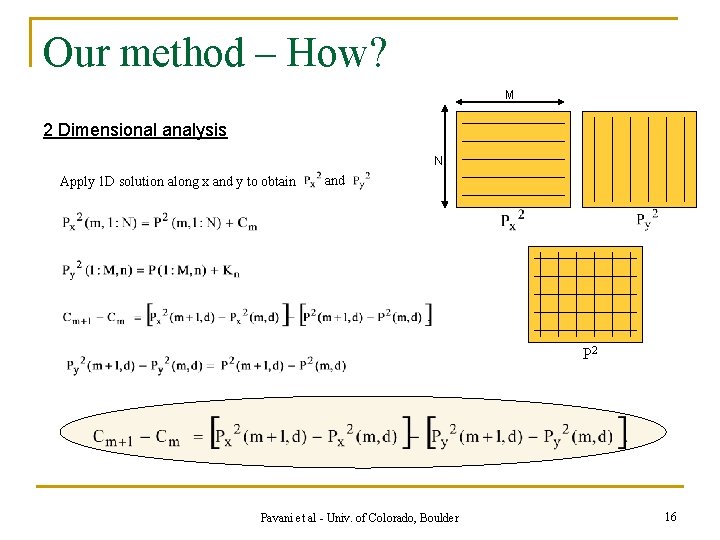
Our method – How? M 2 Dimensional analysis N Apply 1 D solution along x and y to obtain and P 2 Pavani et al - Univ. of Colorado, Boulder 16

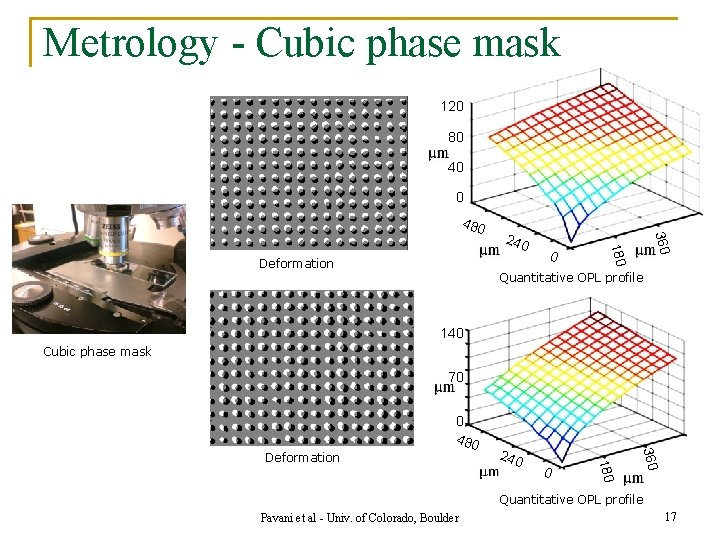
Metrology - Cubic phase mask 120 80 40 0 0 180 Deformation 240 360 480 Quantitative OPL profile 140 Cubic phase mask 70 0 360 240 180 Deformation 0 480 Quantitative OPL profile Pavani et al - Univ. of Colorado, Boulder 17