Quantitative Methods Regression Regression Examples for linear regression

Quantitative Methods Regression

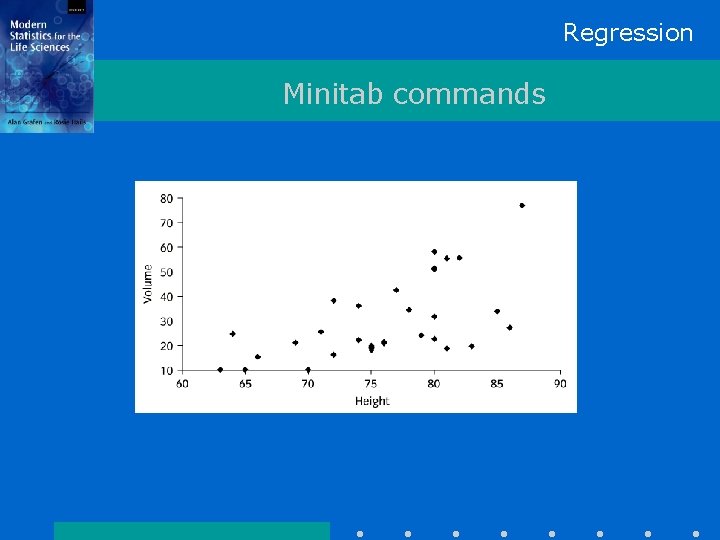
Regression Examples for linear regression • Do more brightly coloured birds have more parasites? • How should we estimate merchantable volume of wood from the height of a living tree? • How is pest infestation late in the season affected by the concentration of insecticide applied early in the season?

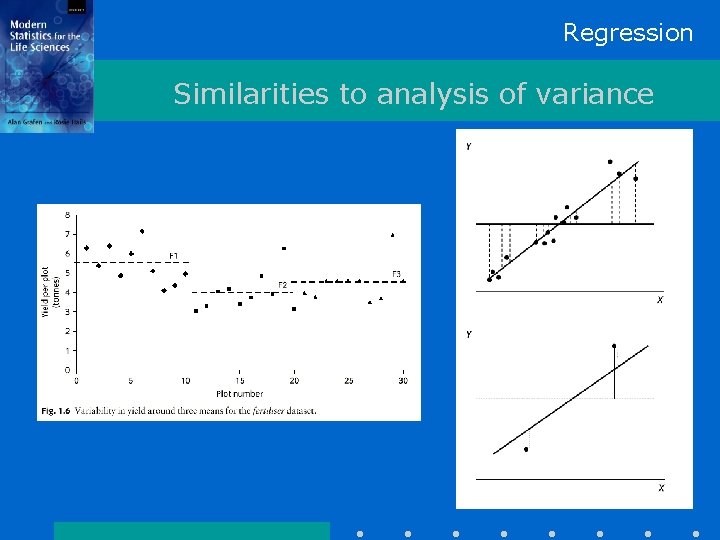
Regression Similarities to analysis of variance

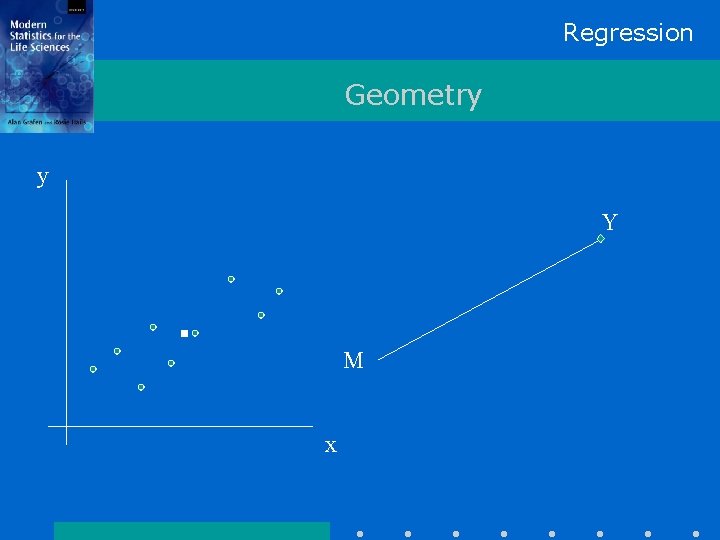
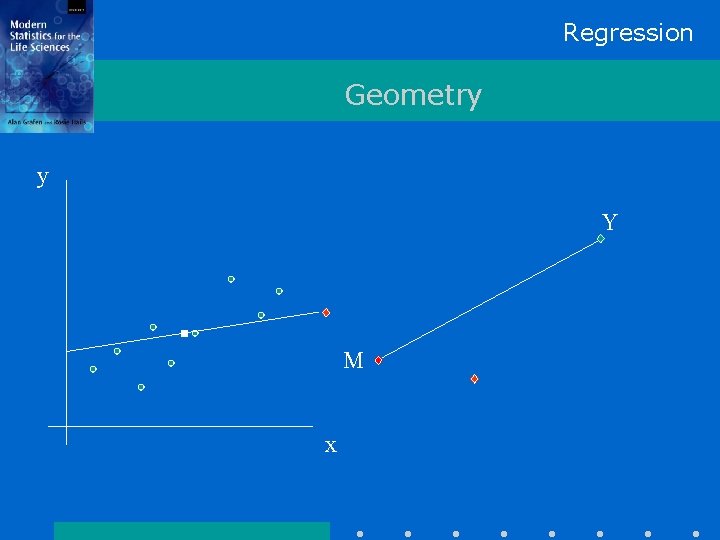
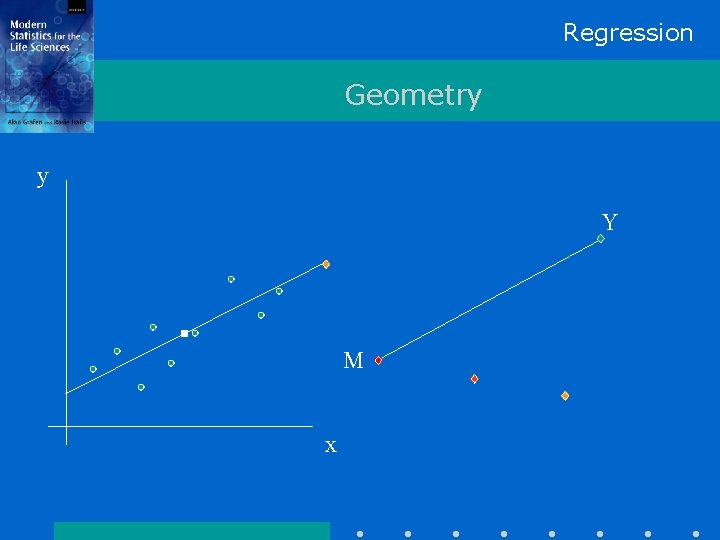
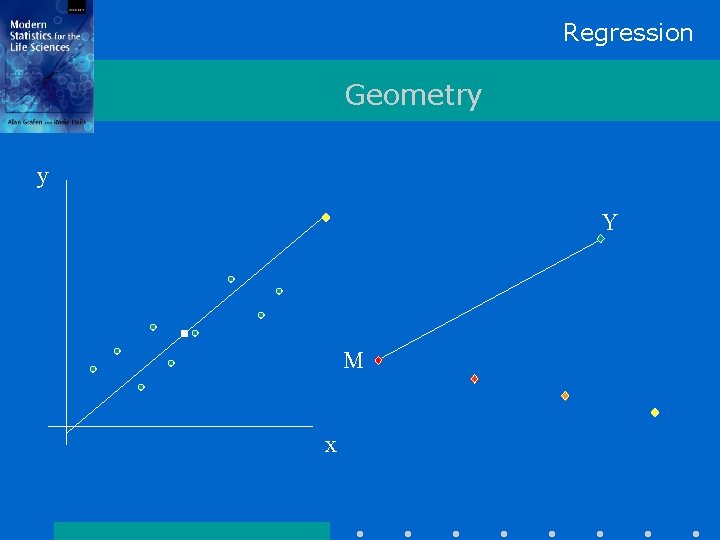
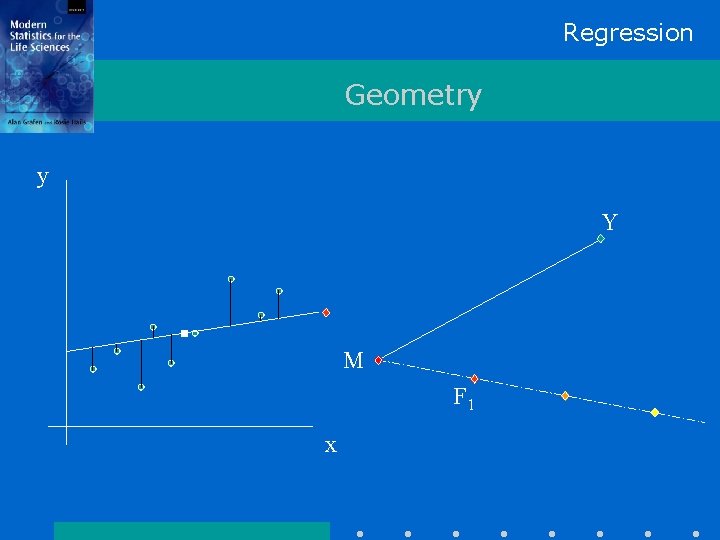
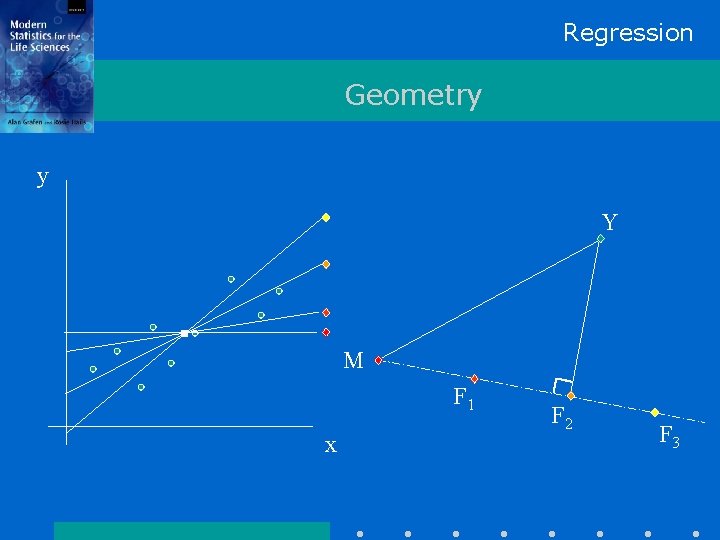
Regression Geometry y Y M x

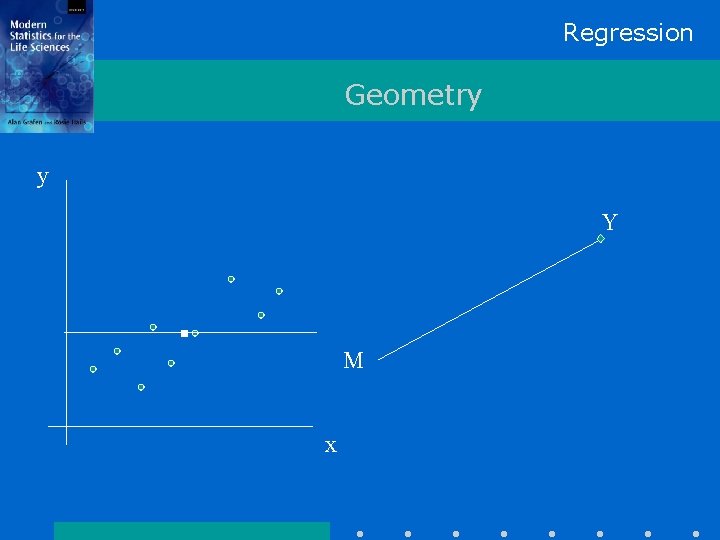
Regression Geometry y Y M x

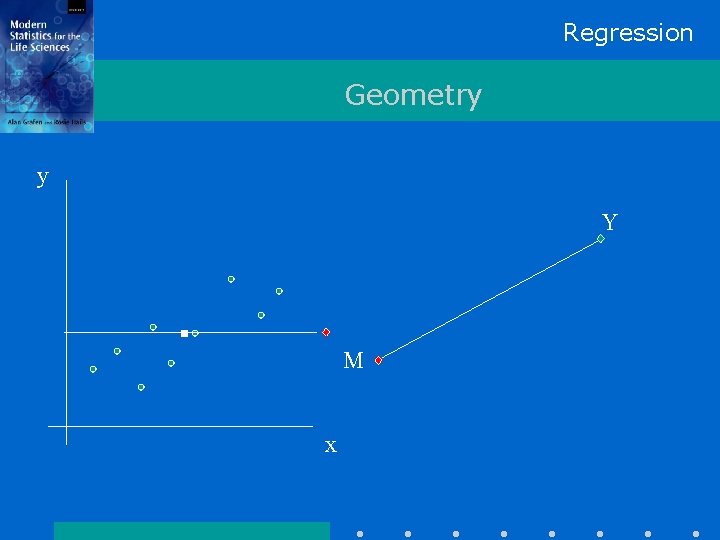
Regression Geometry y Y M x

Regression Geometry y Y M x

Regression Geometry y Y M x

Regression Geometry y Y M x

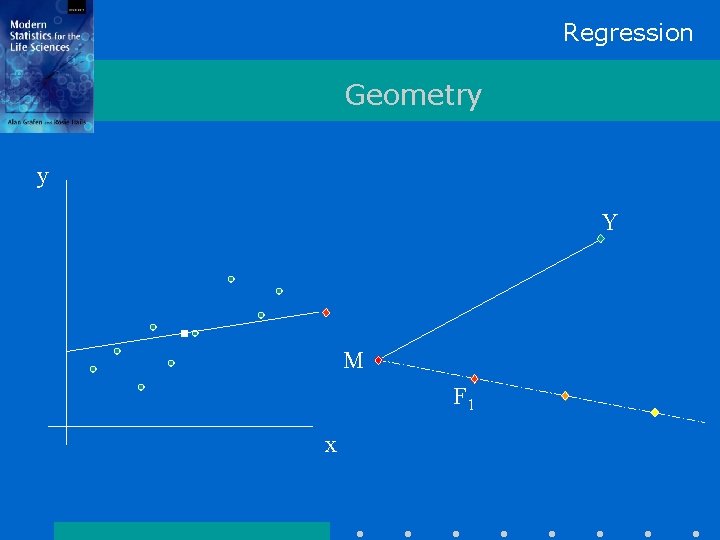
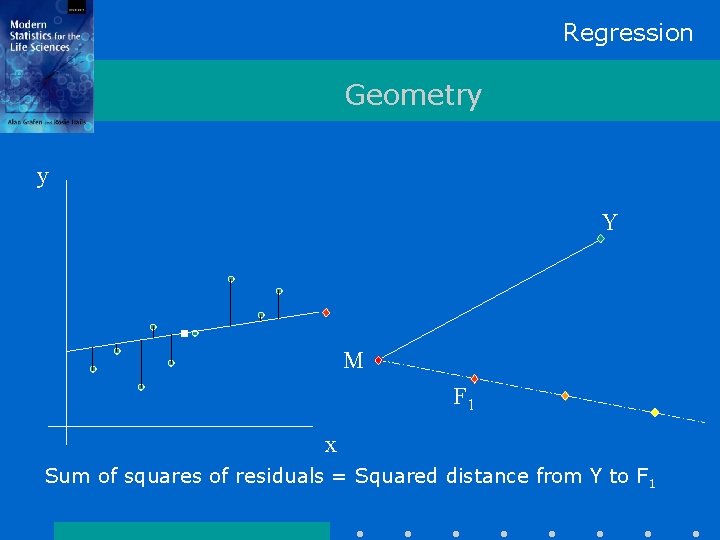
Regression Geometry y Y M F 1 x

Regression Geometry y Y M F 1 x

Regression Geometry y Y M F 1 x Sum of squares of residuals = Squared distance from Y to F 1

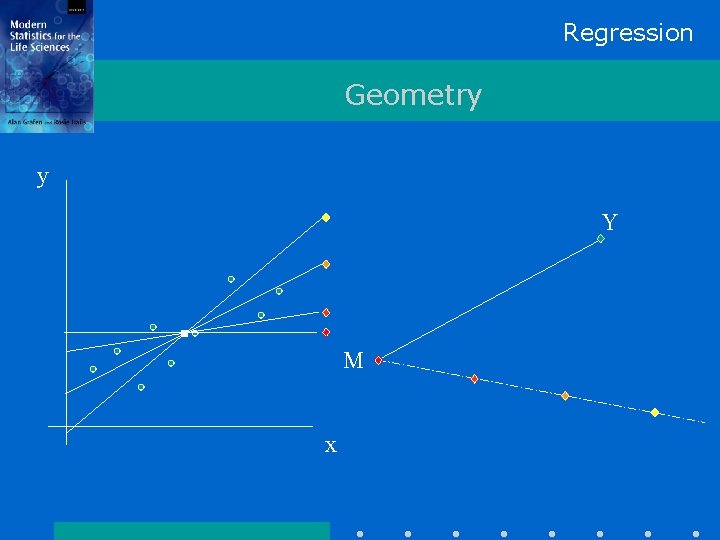
Regression Geometry y Y M x

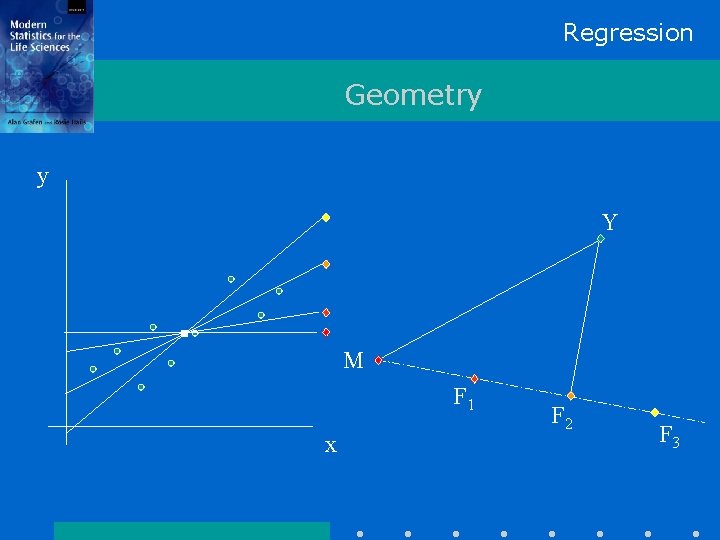
Regression Geometry y Y M F 1 x F 2 F 3

Regression Geometry y Y M F 1 x F 2 F 3

Regression Geometry

Regression Geometry

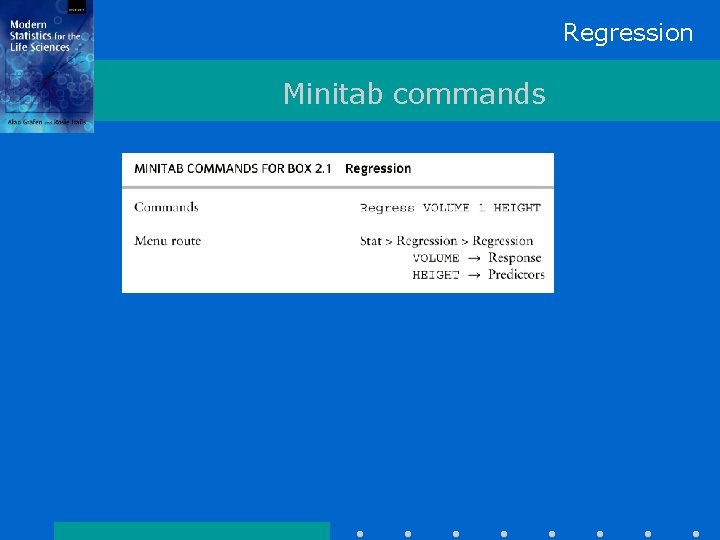
Regression Minitab commands

Regression Minitab commands

Regression Minitab commands

Regression Minitab commands Minitab Supplement is in a PDF file in the same directory as the dataset.

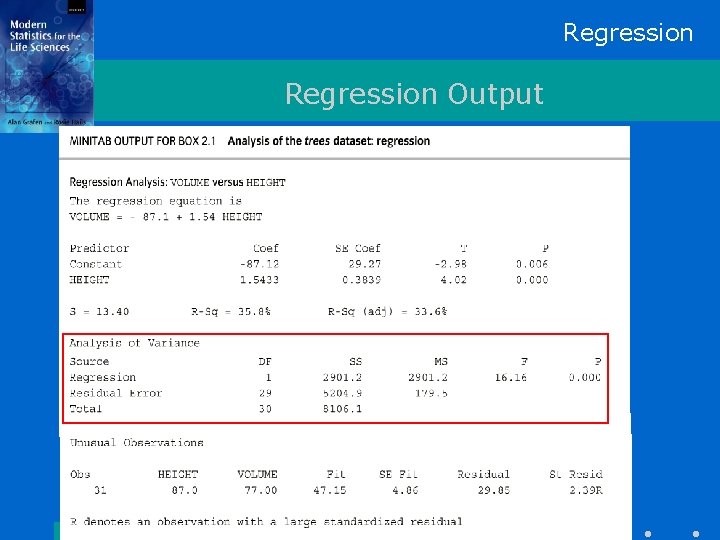
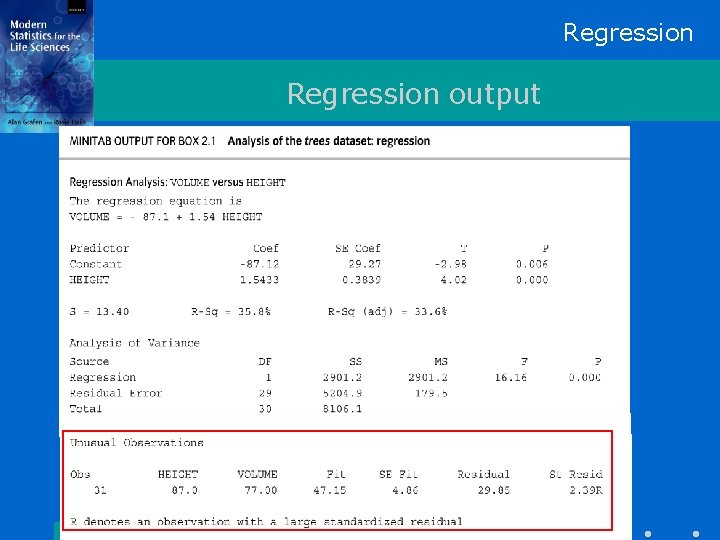
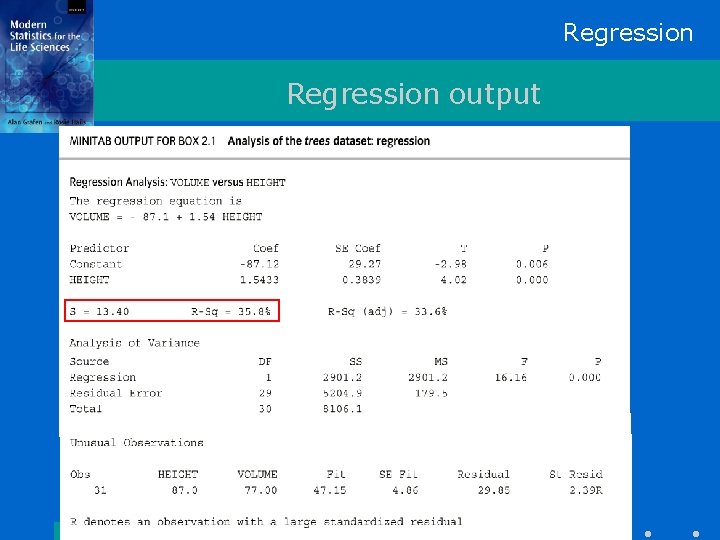
Regression Output

Regression Output

Regression Output

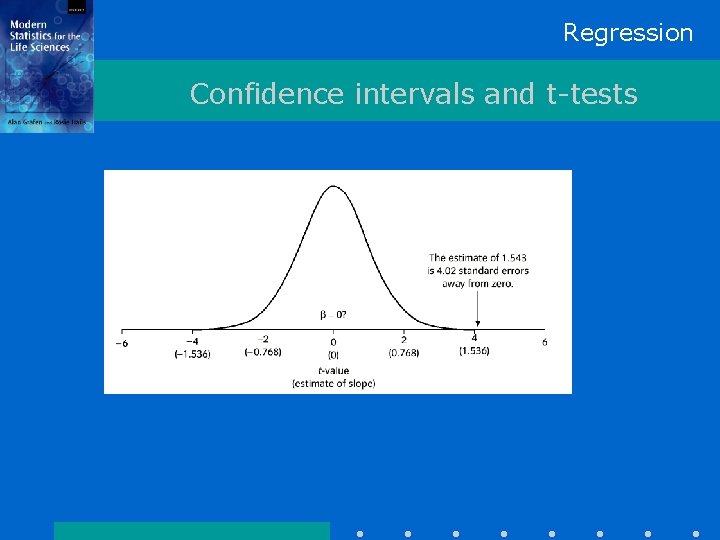
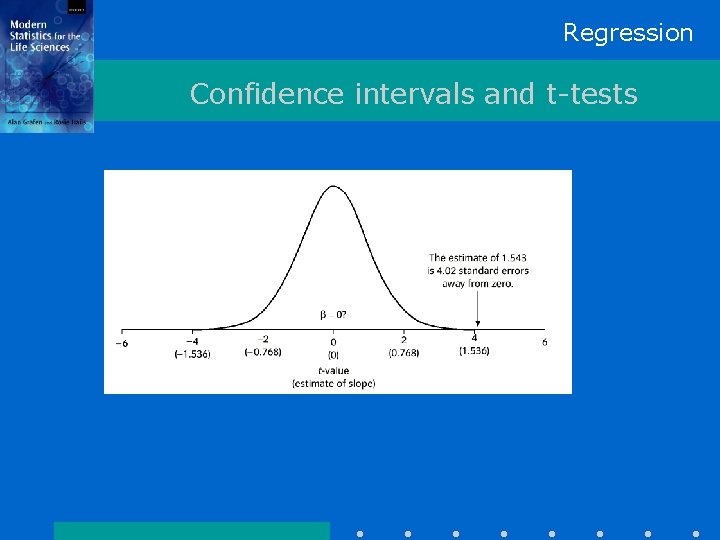
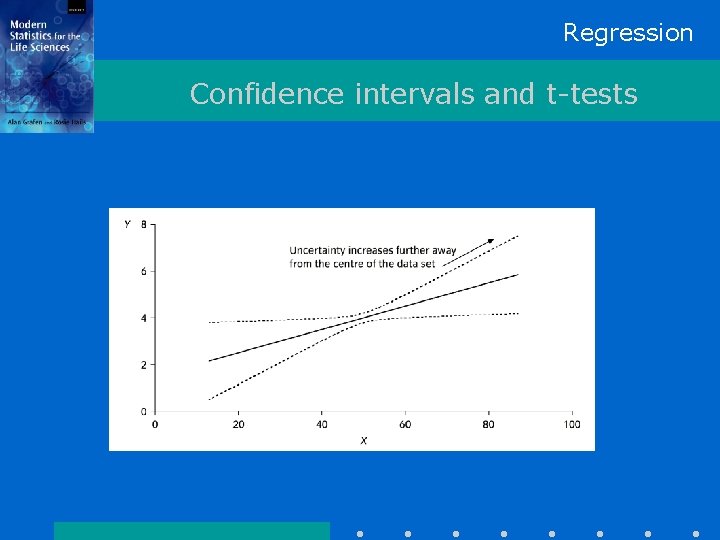
Regression Confidence intervals and t-tests

Regression Confidence intervals and t-tests estimate ± tcrit Standard Error of estimate Coef ± tcrit (on 29 DF) SECoef 1. 5433 ± 2. 0452 0. 3839 = (0. 758, 2. 328) tcrit is always on Error degrees of freedom

Regression Confidence intervals and t-tests

Regression Confidence intervals and t-tests t = distance between estimate and hypothesised value, in units of standard error vs

Regression Confidence intervals and t-tests

Regression Confidence intervals and t-tests

Regression output

Regression output

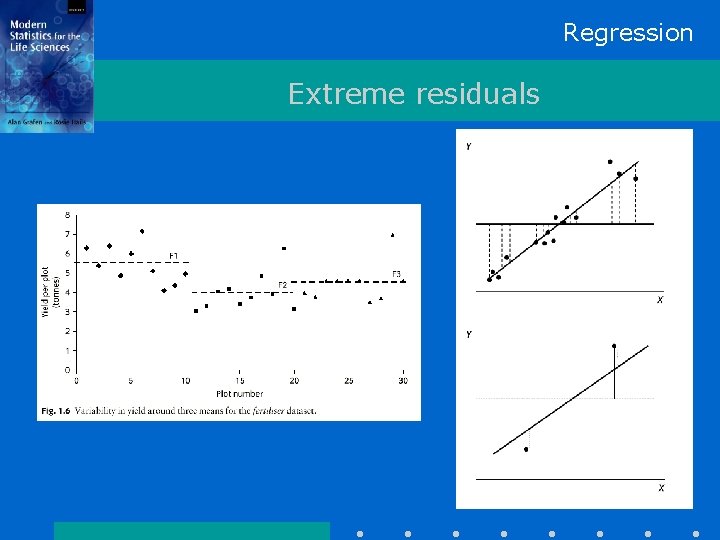
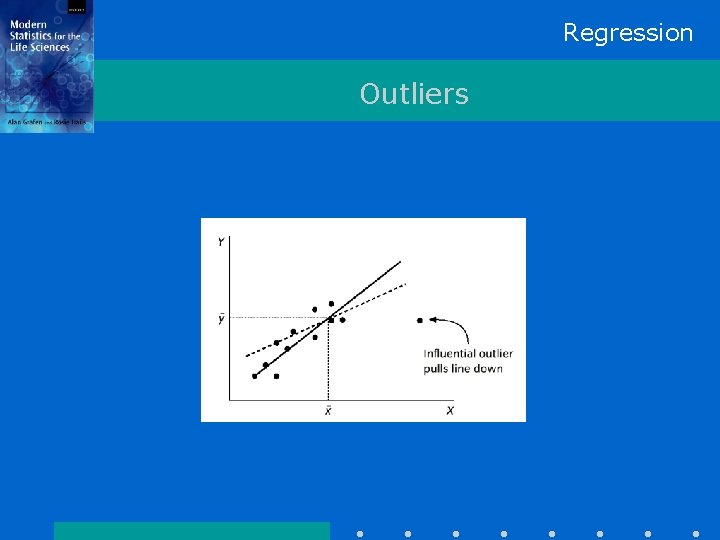
Regression Extreme residuals

Regression Outliers

Regression output

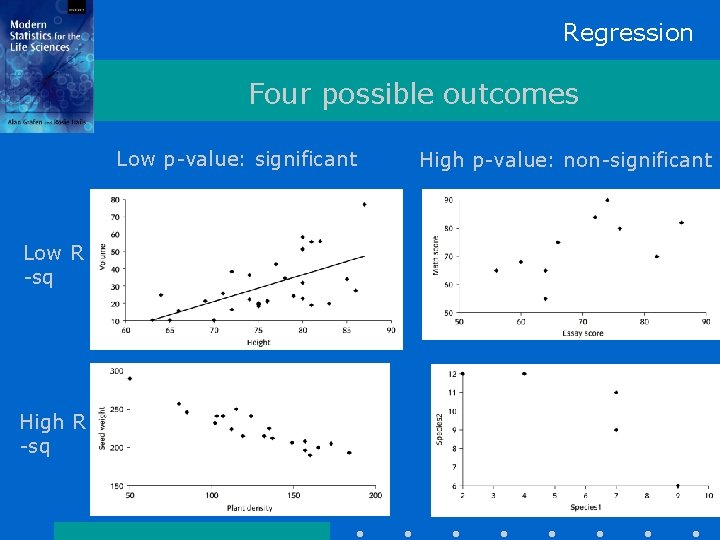
Regression Four possible outcomes Low p-value: significant Low R -sq High p-value: non-significant

Regression Difference from analysis of variance Continuous vs Categorical • Continuously varying • Values have meaning as numbers • Values are ordered • Interpolation makes sense • Examples: – height – concentration – duration • Discrete values • Values are just “names” that define subsets • Values are unordered • Interpolation is meaningless • Examples – drug – breed of sheep – sex

Regression Why linear? • Not because relationships are linear • Good simple starting point - cf recipes • Approximation to a smoothly varying curve

Regression Last words… • Regression is a powerful and simple tool, very commonly used in biology • Regression and ANOVA have deep similarities • Learn the numerical skills of calculating confidence intervals and testing for non-zero slopes.

Regression Last words… • Regression is a powerful and simple tool, very commonly used in biology • Regression and ANOVA have deep similarities • Learn the numerical skills of calculating confidence intervals and testing for non-zero slopes. Next week: Models, parameters and GLMs Read Chapter 3