Quantifying measurement error Blake Laing Southern Adventist University

I uncertainty Measurements have no meaning without a quantified experimental error/uncertainty

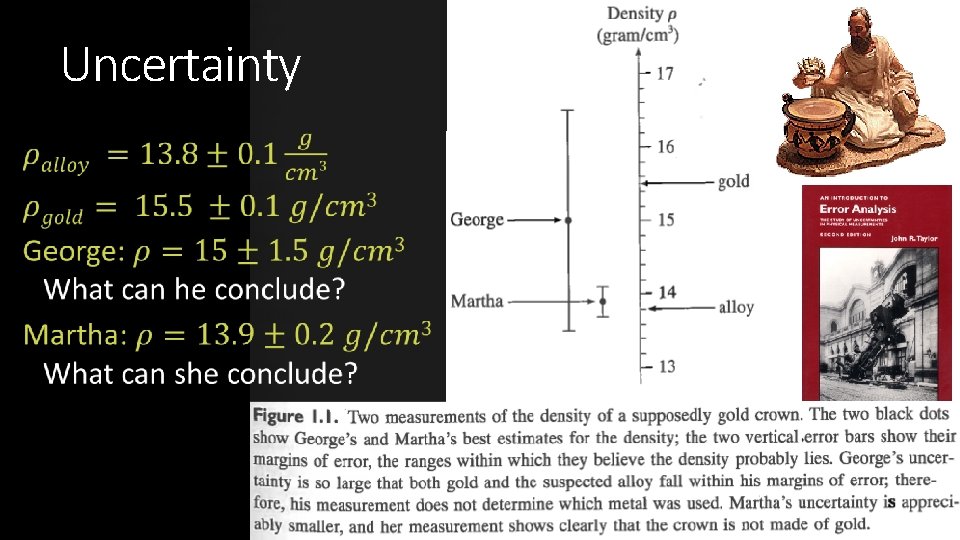
Uncertainty

Uncertainty due to measurement error A personal error is a mistake. No need to quantify, but we should be able to recognize mistaken data Two other measurement errors which are not accidental Random error Causes repeated measurements to be different Causes wide “margin of error” Systematic error Repeated measurements are consistent All measurements are shifted in a predictable way Can be recognized and corrected by “shifting back”

Precision “how close to each other” Accuracy “how close to expected” Random error Different error every time Limits precision Systematic error Same error every time Limits accuracy Precision Accuracy is not precision Accuracy

Random error Quantified by statistics

Statistics in real life If weekly average > 120 mg/d. L, must take insulin Same breakfast: toast with almond butter Morning blood glucose mass concentration glucose day (mg/d. L) 1 110 2 119 Different results 3 7 13 129 90 Summary Max: 129 mg/d. L Min: 90 mg/d. L Mean: 109. 5 mg/d. L

Random or systematic error? 4 Frequency 3 2 1 0 85 2 2 1 1 0 90 95 100 105 110 115 120 125 Blood glucose (mg/d. L) (bin maximum) 0 135

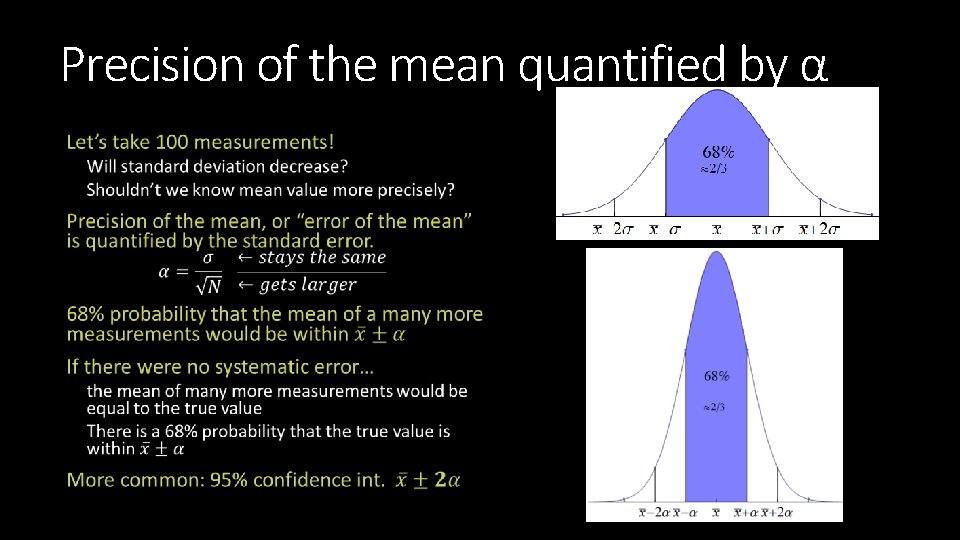
Precision of the mean quantified by α

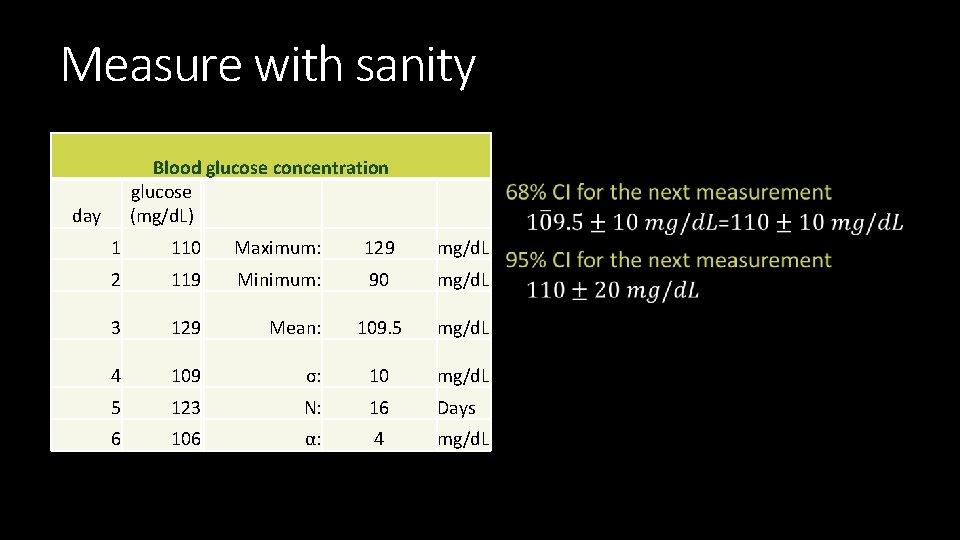
Measure with sanity Blood glucose concentration glucose (mg/d. L) day 1 110 Maximum: 129 mg/d. L 2 119 Minimum: 90 mg/d. L 3 129 Mean: 109. 5 mg/d. L 4 109 σ: 10 mg/d. L 5 123 N: 16 Days 6 106 α: 4 mg/d. L

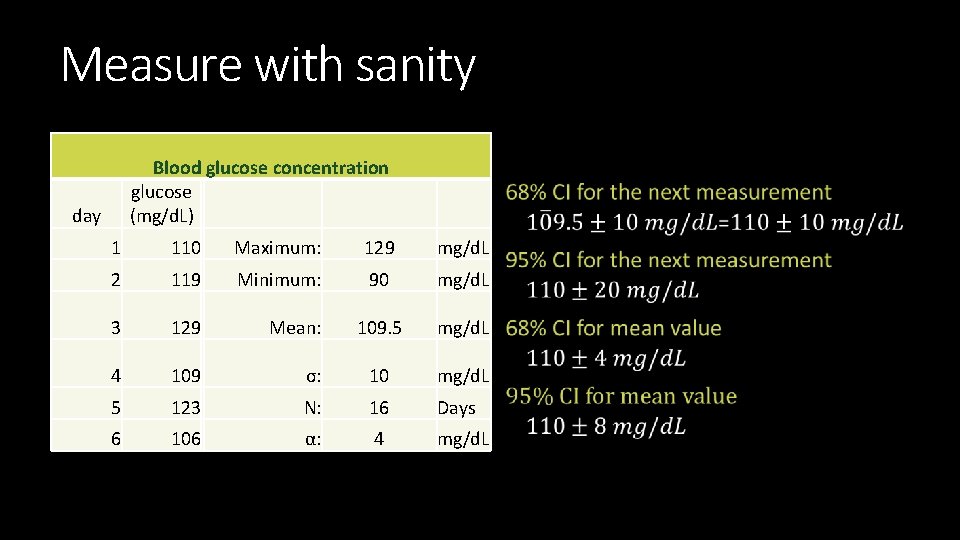
Measure with sanity Blood glucose concentration glucose (mg/d. L) day 1 110 Maximum: 129 mg/d. L 2 119 Minimum: 90 mg/d. L 3 129 Mean: 109. 5 mg/d. L 4 109 σ: 10 mg/d. L 5 123 N: 16 Days 6 106 α: 4 mg/d. L

Systematic error Comparison to expectation

Systematic error: compare to “known”

Compared to what? COMPARE ABS. ERR. TO EXPECTATION COMPARE TO RANDOM ERROR IN HOME DEVICE

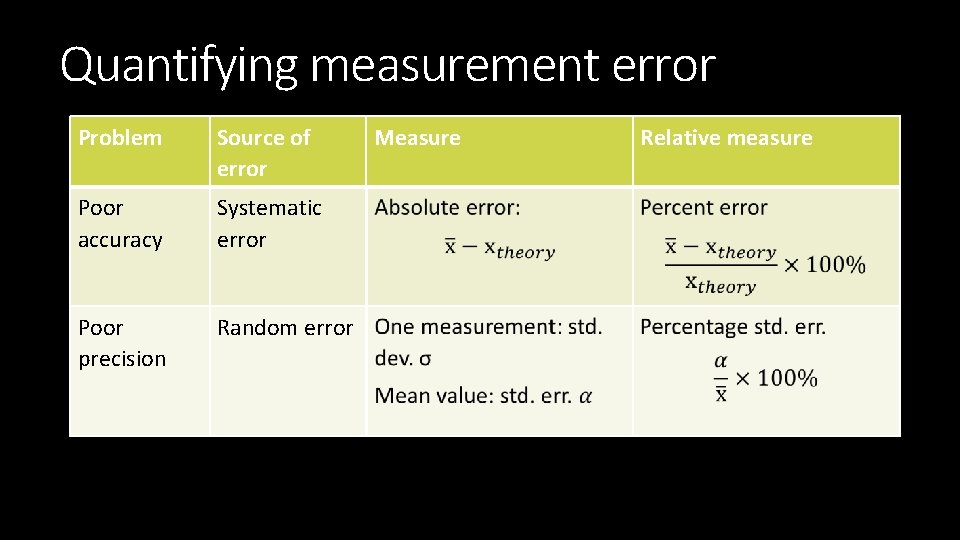
Quantifying measurement error Problem Source of error Poor accuracy Systematic error Poor precision Random error Measure Relative measure

Notes

Experimental notes

Advice from previous students “Take the time to get well acquainted with standard deviation and standard error on your first few labs. . . you'll be seeing them all year!” “Learn how to quantify measurements in the beginning - believe me. I didn't fully learn how to use the tools of the trade till the beginning of the second semester, and it would have paid to learn it first. ” “Know the significant figures for sure: locking in the understanding at the start of the semester saves you A LOT of points. ”

Notes from the reader Need precise, quantitative answers to questions Less wordy “fluff”, more equations/numbers. In every questions it is implied to use or refer to the appropriate “tool for the job”, such as percent error. Need careful articulation of words to be able to have a carefully-articulated understanding. Common mistakes on significant figures use calculated standard error to determine correct sig figs on the mean When calculating percent error, watch for the loss of sig figs when subtracting

Because I always back up my argument with an incisive quantitative analysis.

Quantifying measurement error necessary to form quantitative conclusions

See Dr. Laing bleed for science

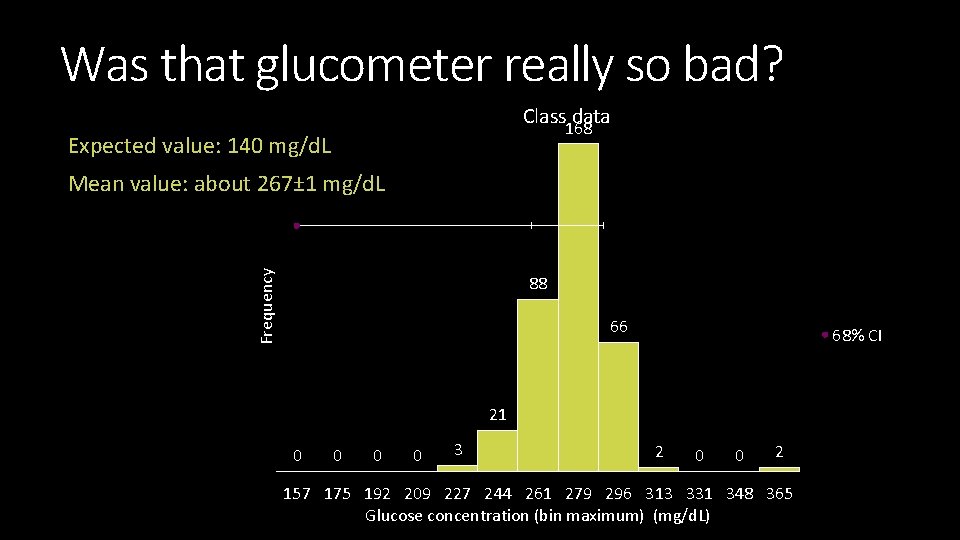
Was that glucometer really so bad? Class data 168 Expected value: 140 mg/d. L Frequency Mean value: about 267± 1 mg/d. L 88 66 68% CI 21 0 0 3 2 0 0 2 157 175 192 209 227 244 261 279 296 313 331 348 365 Glucose concentration (bin maximum) (mg/d. L)

A faulty assumption is a systematic error Two hours after breakfast concentration (mg/d. L) Trial 1 104 N= 32 2 99 Max= 110 mg/d. L 3 106 Min= 83 mg/d. L 4 102 5 99 Mean= 6 94 σ= 6 mg/d. L 7 94 α= 1 mg/d. L 94. 41 mg/d. L Aqueous glucose vs whole blood has a p. H of about 7. 4 (basic) Distilled water has a p. H < 7 (acidic) Different density Standard deviation about half of aqueous glucose solution What is the 95% CI for each measurement? What is the 95% CI for mean?

Reader notes

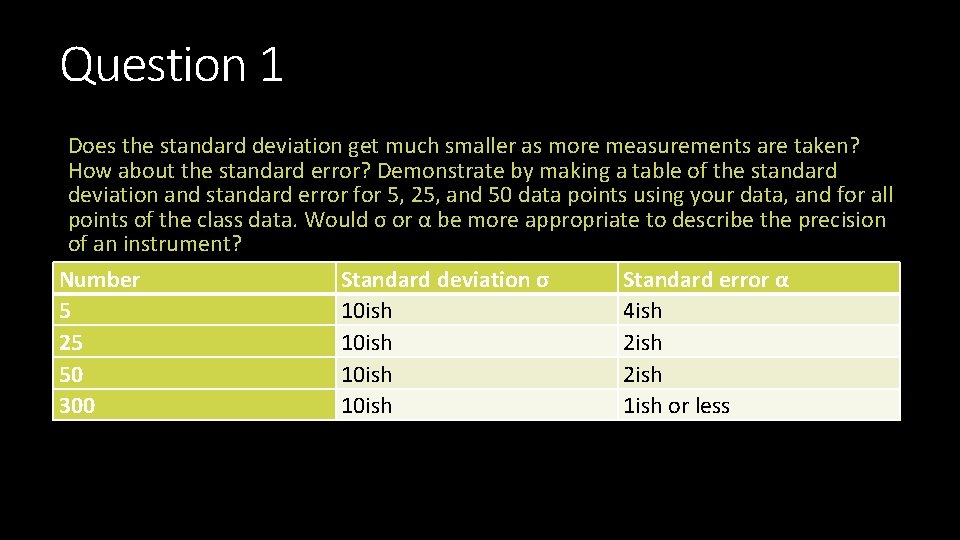
Question 1 Does the standard deviation get much smaller as more measurements are taken? How about the standard error? Demonstrate by making a table of the standard deviation and standard error for 5, 25, and 50 data points using your data, and for all points of the class data. Would σ or α be more appropriate to describe the precision of an instrument? Number Standard deviation σ Standard error α 5 10 ish 4 ish 25 10 ish 2 ish 50 10 ish 2 ish 300 10 ish 1 ish or less

Notes

Post-analysis