Quantifier Elimination via Functional Composition JieHong Roland Jiang

Quantifier Elimination via Functional Composition Jie-Hong Roland Jiang Dept. of Electrical Eng. / Grad. Inst. of Electronics Eng. National Taiwan University Taipei 10617, Taiwan 2009/6/30 CAV 2009 1

Outline l Motivations l Prior work l Quantifier elimination by functional composition l l Propositional logic Predicate logic l Experimental results l Conclusions 2009/6/30 CAV 2009 2

Introduction l Quantifier elimination transforms a quantified formula, e. g. , x 1 x 2 x 3 xn , into an equivalent quantifier-free formula l can be preferable to x 1 x 2 x 3 xn E. g. , l Properties of can be reasoned more easily l can be treated as a synthesis result for implementation 2009/6/30 CAV 2009 3

Introduction l QE examples l Gauss elimination for systems of linear equalities l Fourier-Motzkin elimination for systems of linear inequalities l Cylindrical algebraic decomposition for systems of polynomial inequalities 2009/6/30 CAV 2009 4

Motivations l QE arises in many contexts, including computation theory, mathematical logic, optimization, … Constraint reduction l Quantified Boolean Formula (QBF) solving l 2009/6/30 CAV 2009 5

Main focus l Propositional l 2009/6/30 logic Quantifier elimination for QBFs CAV 2009 6

Prior work l Formula expansion l l l y (x, y) = (x, 0) (x, 1) BDD, AIG based image-computation [Coudert 90][Pigorsch 06] Normal-form conversion l Existential (universal) quantification is computationally trivial for disjunctive (conjunctive) normal formulas l l l Formula conversion between CNF and DNF [Mc. Millan 02] Solution enumeration l l l Simply remove from the formula the literals of variables to be quantified E. g. , x 1[(x 1 x 2 x 3)( x 1 x 3)(x 2 x 4)] = (x 2 x 3)(x 2 x 4) Compute (x) = y (x, y) by enumerating all satisfiable assignments on x SAT-based image computation, e. g. , [Ganai 04] Yet another way? 2009/6/30 CAV 2009 7

Question a quantified formula y (x, y), what should a function f be such that (x, f(x)) = y (x, y)? l Given l I. e. , 2009/6/30 QE by functional composition CAV 2009 8

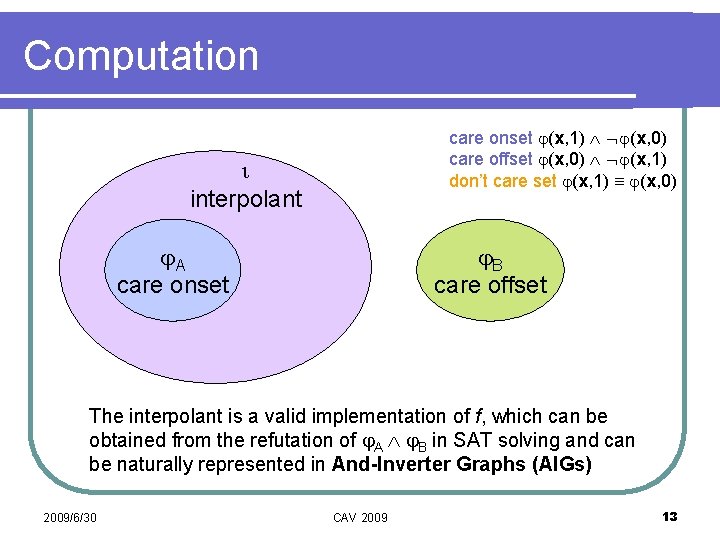
Answer l (x, f(x)) = y (x, y) if and only if l f has care onset (x, 1) (x, 0) care offset (x, 0) (x, 1) don’t care set (x, 1) (x, 0) l In other words, ( (x, 1) (x, 0)) f ( (x, 0) (x, 1)) l Such f always exists 2009/6/30 CAV 2009 9

Problem formulation l For universal quantification y (x, y) = y (x, y) = (x, f(x)) = (x, f(x)) l l f has care onset (x, 1) (x, 0) care offset (x, 0) (x, 1) don’t care set (x, 1) (x, 0) So by computing composite functions f, one can iteratively eliminate the quantifiers of any QBF 2009/6/30 CAV 2009 10

Computation lf can be computed by l Binary decision diagrams (BDDs) l l 2009/6/30 Not scalable for large Craig interpolation CAV 2009 11

Craig interpolation l (Propositional logic) For A B unsatisfiable, there exists an interpolant of A w. r. t. B such that 1. A 2. B is unsatisfiable 3. refers only to the common variables of A and B 2009/6/30 CAV 2009 12

Computation care onset (x, 1) (x, 0) care offset (x, 0) (x, 1) don’t care set (x, 1) (x, 0) interpolant A care onset B care offset The interpolant is a valid implementation of f, which can be obtained from the refutation of A B in SAT solving and can be naturally represented in And-Inverter Graphs (AIGs) 2009/6/30 CAV 2009 13

Composition vs. expansion l Is (x, f(x)) better than (x, 0) (x, 1) ? f x x in terms of AIGs, where structurally identical nodes are merged 2009/6/30 CAV 2009 14

Composition vs. expansion l [ ] Consider simplifying (x, 1) in (x, 0) (x, 1) using (x, 0) as don’t care onset (x, 1) (x, 0) care offset (x, 1) (x, 0) In contrast to f with care onset (x, 1) (x, 0) care offset (x, 0) (x, 1) For existential quantification, composition can be much better than expansion for sparse (due to simple interpolants) 2009/6/30 CAV 2009 15

Composition vs. expansion l [ ] Consider simplifying (x, 1) in (x, 0) (x, 1) using (x, 0) as don’t care onset (x, 1) (x, 0) care offset (x, 1) (x, 0) In contrast to f with care onset (x, 1) (x, 0) care offset (x, 0) (x, 1) For universal quantification, composition can be much better than expansion for dense (due to simple interpolants) 2009/6/30 CAV 2009 16

Generalization to predicate logic l For a language L in predicate logic under structure (interpretation) I, |=I x( y (x, y) = F (x, Fx)) l QE is possible if such function F is finitely expressible in the language l l l 2009/6/30 If y (x, y) = (x, fx), then (a, b) y (a, y) is satisfied for any a, b with f(a)=b If for any a, b with f(a)=b satisfies (a, b) y (a, y), then y (x, y) = ( i (x, fix)), where f = fi if i holds {(a, b) | (a, b) y (a, y)} characterizes the flexibility of f, which can be exploited to simplify QE CAV 2009 17

Generalization to predicate logic Example x(a x 2+c=0) over the real number f(a, c) = (–c/a)1/2 – if c/a 0 if c/a > 0 Taking f(a, c) = (((–c/a)2)1/2, this quantified formula is equivalent to a ((((–c/a)2)1/2)2+c=0 2009/6/30 CAV 2009 18

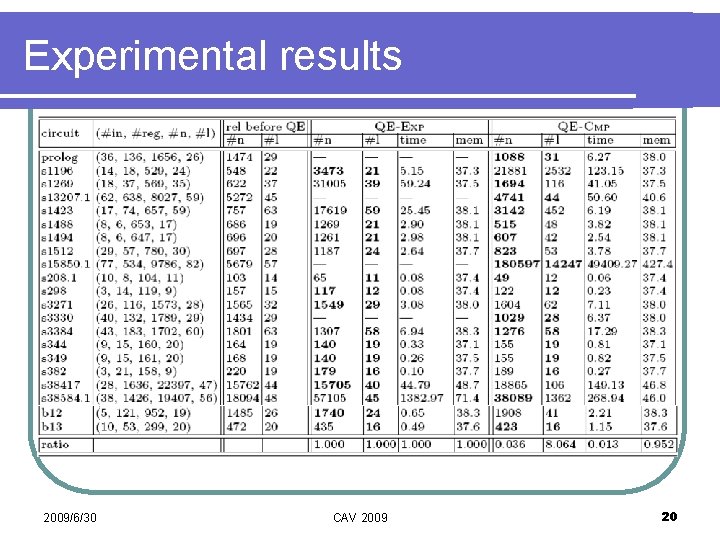
Experiments l Given a sequential circuit, we compute its transition relation with input variables being quantified out, i. e. , x [ i (si' i(x, s))] Simple quantification scheduling applied l AIG minimization applied l 2009/6/30 CAV 2009 19

Experimental results 2009/6/30 CAV 2009 20

Discussion l Expansion l vs. composition based QE Analogy with two-level vs. multi-level circuit minimization l Relaxing level constraints admits more compact circuit representation l Sparsity may play an essential role in the effectiveness of composition-based QE 2009/6/30 CAV 2009 21

Conclusions l Quantifier elimination with functional composition can be effective at least for some applications (where the sparsity condition holds) l Future work Find more applications l QE in predicate logic l 2009/6/30 CAV 2009 22

Thanks for your attention! 2009/6/30 CAV 2009 23

Questions? 2009/6/30 CAV 2009 24