Quality Control Quality Assurance QUALITY ASSURANCE Quality Assurance

Quality Control & Quality Assurance

QUALITY ASSURANCE • Quality Assurance (QA): the practice which encompasses all activities, procedures, formats of activities directed towards ensuring that a specified quality or product is achieved or maintained. • QA involves in every step in the analysis process from the initial ordering of a test and the collection of the patient sample (pre analytic), analysis of the sample (analytic), and finally the distribution of result to the proper destination. • QA program involves every person in the lab. From the director to the lab helpers, also includes everyone who has contributed to the enterprise such as the phlebotomy team and data processors.

Roles of QA: 1. Select the most accurate and precise analytical methods, in a time period that is most helpful to the physician. 2. Adequately train and supervise the activities of the lab personnel and conduct them with continuing education sessions. 3. Good instruments and institute a regular maintenance program. 4. Good quality control program, which is concerned with the analytical phase of QA. 5. Make available printed procedures for each method, with explicit directions, an explanation of the chemical principles and a listing of the reference values.

Quality Control (QC) • Statistical QC is concerned with the analytical phase of quality assurance. • It monitors the overall reliability of lab results in terms of accuracy and precision according to the criteria specified for each measurement.

WHY IS QUALITY CONTROL NECESSARY? • Proper validation and standardization of the assay. • A reliable endocrine monitoring program. Subsequent assessment of assay quality and consistency is absolutely necessary to assure the biological relevance of results. • For every assay system there is an inherent level of error which must be accepted. A quality control program indicates when that level of error becomes unacceptable.

Control specimens q The simplest, most straight forward way to check the reproducibility of a method is by including control specimens in the run. q If control serum or urine are included with patient's samples, and observed results are the expected results, we can feel confident about the assay and can probably safely assume that the results on the patient's samples are also correct. q Control specimens are often consisting of lyophilized pooled sera, urine or pituitary extracts…. . , which may be in the normal rang or abnormal when reconstituted. q The test results are valid only if all controls are within the specified ranges

q It is recommended to do the test sample duplicate. q The controls should be treated as unknowns and values determined in every test procedure performed. q QC specimens may be commercial prepared or by the laboratory By pooling plasma, freezing, then to be used when needed. q A quality control product usually contains many different analytes. For example a general endocrine control can contain any number of hormone analytes including TSH, FSH, LH, Testosterone and others.

q How to prepare a control? o prepare a large pool projected to last for several years. o divide the material into small aliquots to avoid repeated freeze-thawing. o keep the aliquots in a safe freezer (preferably one with a temperature alarm). o store all materials, including samples, in a no frost-freezer. o do not allow controls to run out before making up new controls.

characteristics of good control: 1. The composition should be as similar to the patient sample. 2. The concentration should be stable under storage for long period of time. 3. Material should be low vial-to- vial variability. 4. After vial has been opened and material prepared, it should remain stable for the period of use. 5. The material should be reasonably priced (Not expensive). 6. The material should be available in large quantities.

• QC can be divided into two major types: 1. Internal QC (intra laboratory QC): This primarily monitors the day to-day performance of laboratory results, precision. 2. External QC (inter laboratory QC): which primarily monitors the accuracy of the results

The statistical process requires: • Regular testing of quality control products along with patient samples. • Comparison of quality control results to specific statistical limits (ranges). • Note: The result may be – quantitative (a number) or – qualitative, (positive or negative) or – semi-quantitative (limited to a few different values).

• Systematic error or Analytical: Which is usually due to an analytical factor (instrumental, operational or errors of method) this bias (inaccuracy) can be determined and corrected. • Random error: Lab also subjected to imprecision or random variability

Some Quality Control Techniques • Shift: Is defined as a drift of values from one level of the control chart to another, which may be sudden or gradual and may be due to failure to recalibrate when changing lot numbers of reagent during an analytical process.

• Trend: Is the continuous movements in one direction over six or more consecutive values. Trends are difficult to detect without continual charting, and may start on one side of the mean and move across it or it can occur entirely on one side of the mean this problem is usually due to deterioration of reagents or light source of the instrumentations.

• Dispersion: Values may be within the acceptable range (2 s and 3 s) but are unevenly distributed outside the ± 1 s limits. This is indicating a loss of precision and due to random error.

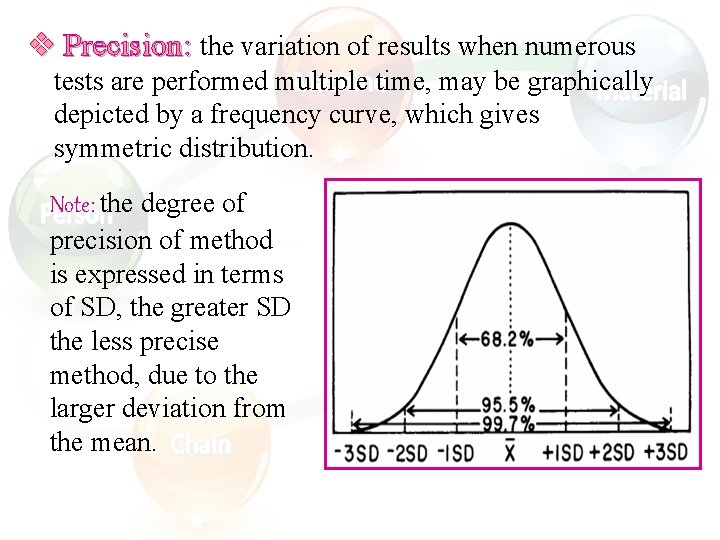
Accuracy and Precision v Accuracy: is defined as the extent to which the mean measurement is close to the true value. The accuracy of a method is generally reflected by it is ability to produce the values of reference samples of known concentration.

v Precision: the variation of results when numerous tests are performed multiple time, may be graphically depicted by a frequency curve, which gives symmetric distribution. Note: the degree of precision of method is expressed in terms of SD, the greater SD the less precise method, due to the larger deviation from the mean.

• Standard deviation: X is the mean Xi is an individual measurement ∑ is the operation of summation • Mean: the average values (the central point). • Median: the middle value within the range. • Mode: the most frequency occurring value.

The coefficient of variation (CV) Ø Is the SD expressed as a percentage of the mean (average) and is more reliable means for comparing the precision at different concentration level of units. • The precision of method varies inversely with the CV; the lower the CV the greater the Precision. • Range of CV < 5 -10% to consider the method is precise. • Variance: less used to express precision, equal squared of SD= (SD)2

• Fluctuations in CV can be caused by: Ø Inaccurate pippeting (ensure pipette tips are sealed to the pipette before use so they draw up to correct volume of liquid) Ø Splashing of reagents between wells Ø Bacterial of fungal contamination of either screen samples or reagents Ø Cross contamination between reagents Ø Temperature variations across the plate. Ensure the plates are incubated in a stable temperature environment away from drafts. Ø Some of the wells dry out. Ensure the plates are always covered at incubation steps

Types of variation(CV) Ø intra-assay CV(<10) • determines the within assay error (the error associated with running the sample in one assay). Most accurately determined by calculating the variation in assaying multiple replicates of one sample throughout the assay (e. g. , n = 10 replicates). • More typically, the average intra-assay CV is calculated from the internal controls assayed at the beginning of the assay.

• A third method is to calculate the average CV of all unknowns run in an assay. If more than one assay has been run for a particular study, then the mean intraassay CVs for those assays should be averaged. Ø inter-assay CV: (<15) • determines the between assay error (the error observed when the sample is run in different assays). • Determined by calculating the variation in values for samples run in every assay. • Within a study can calculate the individual inter-assay CVs for each internal control and then average those numbers.

Causes of variation: • intra-assay CV: generally is the result of the presence of unequal amounts of sample, tracer or antibody (i. e. , poor pipetting, or incomplete mixing of sample or reagents), but also can be due to inconsistencies in counting or decanting. • inter-assay CV: caused by system-related problems like reagent instability, procedural variation or changes in standards (do not allow old standards to run out before making up new standards!).

• rules of thumb for defining acceptable levels of error – Fixed percentage of the CV- often designated as 10% such that all samples with a CV >10% are re-analyzed. – Assay rejection criteria- often subjective, but can involve exclusions based on control values falling within 2 SD of the mean of previous values, or a set proportion of sample CVs being below 10%.

Ø Standard specimen – A substance that can be accurately weighed or measured to produce a solution of an exactly known concentration. – It is used to calculate the concentration of an analyte/s in the sample – Standard vs. calibrator.

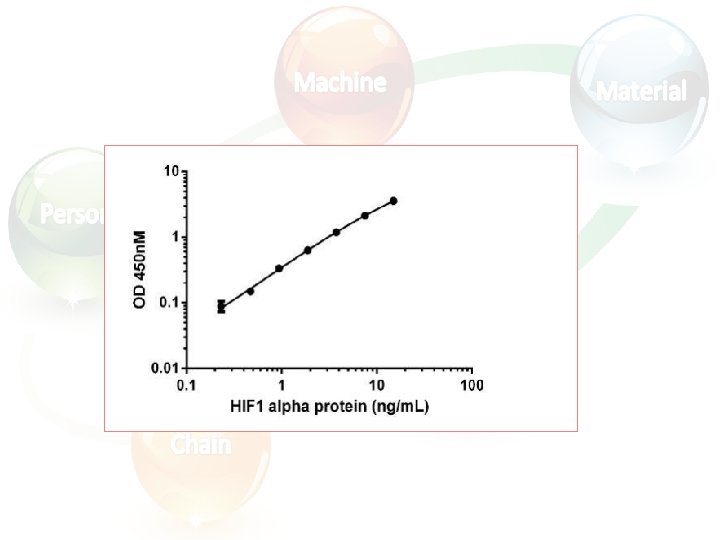
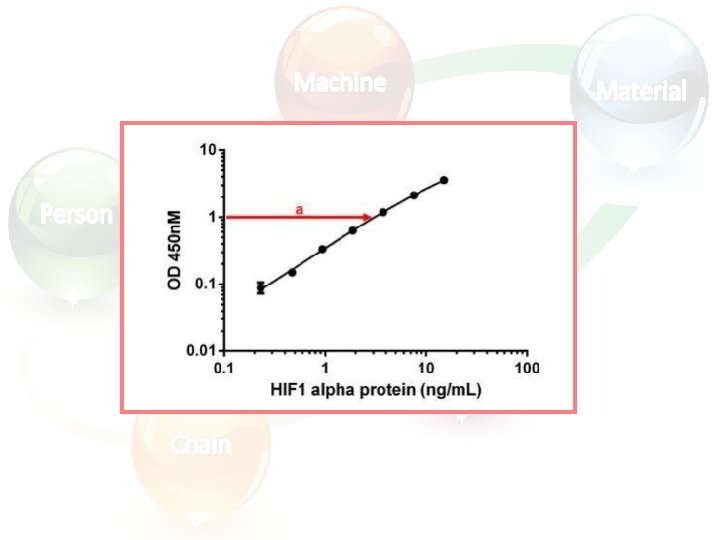
Calculating and evaluating ELISA data • Always run ELISA samples in duplicate or triplicate. This will provide enough data for statistical validation of the results. Many computer programs are now available to help process ELISA results in this way: 1. Calculate the average absorbance values for each set of duplicate standards and duplicate samples. Duplicates should be within 20% of the mean. 2. Standard curve : Create a standard curve by plotting the mean absorbance for each standard concentration (x axis) against the target protein concentration (y axis). Draw a best fit curve through the points in the graph (we suggest that a suitable computer program be used for this).

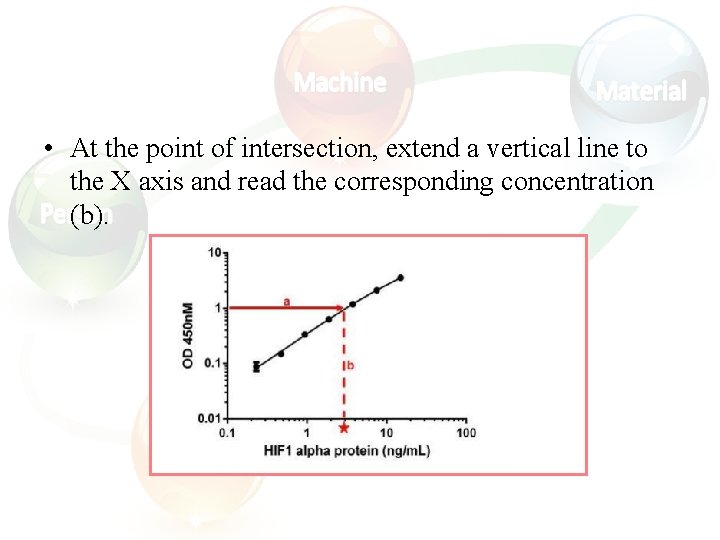
• At the point of intersection, extend a vertical line to the X axis and read the corresponding concentration (b).

Samples that have an absorbance value falling out of the range of the standard curve? ? ? !! For example, samples in the image above where the standard curve has a plateau, are too concentrated and will provide an inaccurate quantification. To obtain an accurate result, these samples should be diluted before proceeding with the ELISA staining. For these samples, the concentration obtained from the standard curve when analyzing the results must be multiplied by the dilution factor.

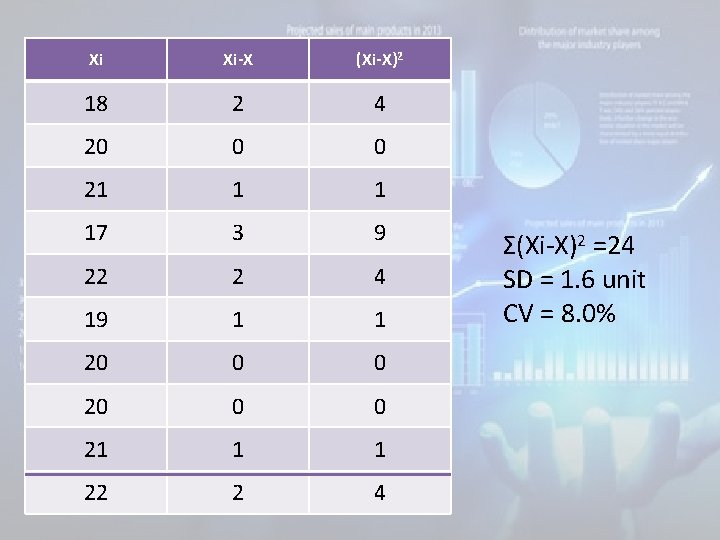
Example (use manual method and computer program – Excel) • The following results was obtained for a sample when assayed several times, 17, 18, 19, 20, 20, 21, 22 Find the mean, SD, CV, Variance?

• Solution: 1. Calculate mean= Σ xn= Σ (18+20+21+17+22+19+20+20+21+22)/10=20. 2. Calculate the difference of each result from the mean. 3. Square the difference. 4. Σ Of squares.

Xi Xi-X (Xi-X)2 18 2 4 20 0 0 21 1 1 17 3 9 22 2 4 19 1 1 20 0 0 21 1 1 22 2 4 Σ(Xi-X)2 =24 SD = 1. 6 unit CV = 8. 0%

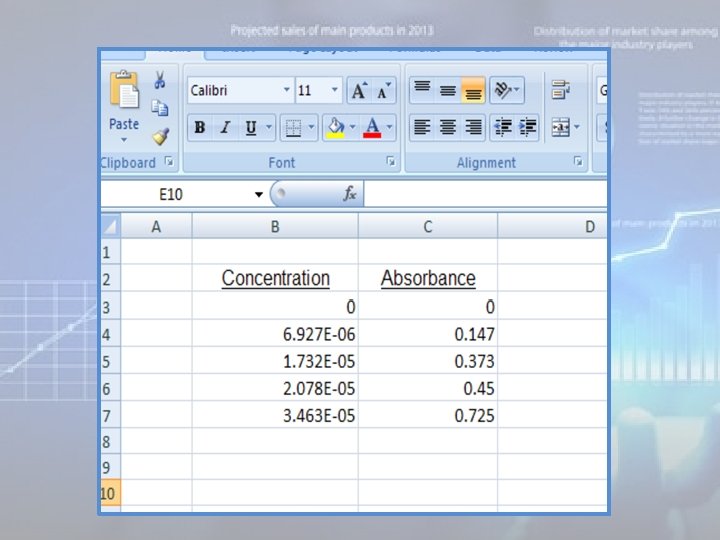
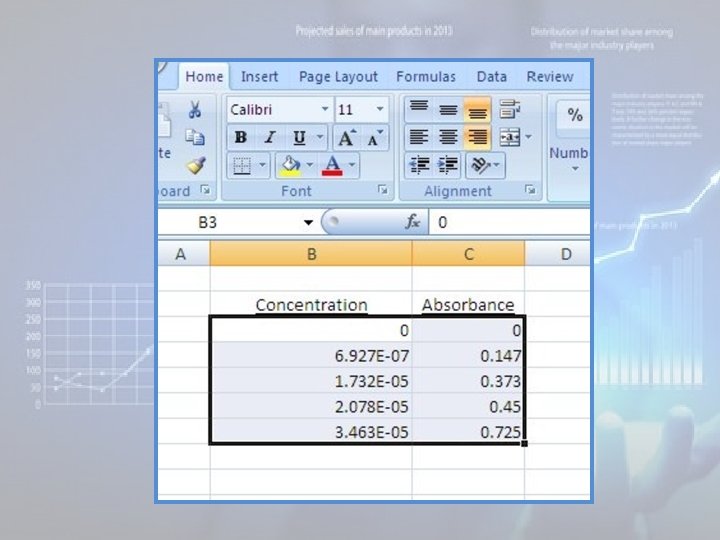
Using Microsoft Excel to plot calibration curve: • There are many different versions of MS Excel, and these instructions may vary slightly in different versions! 1. The first step in creating a graph using Microsoft Excel is entering the data. The data should be in two adjacent columns with the x data in the left column. In the figure below, I have labeled the columns but this is not necessary to create the graph. Note that your absorbance data should include the origin {concentration = zero, absorbance = zero}:

2. Position the cursor on the first X value (i. e. , at the top of the column containing the x values, or "Concentration” values), hold down the left mouse button and drag the mouse cursor to the bottom Y value (i. e. , at the bottom of the column containing the y values, or "Absorbance" values). All of the X-Y values should now be highlighted (do NOT highlight the labels!):

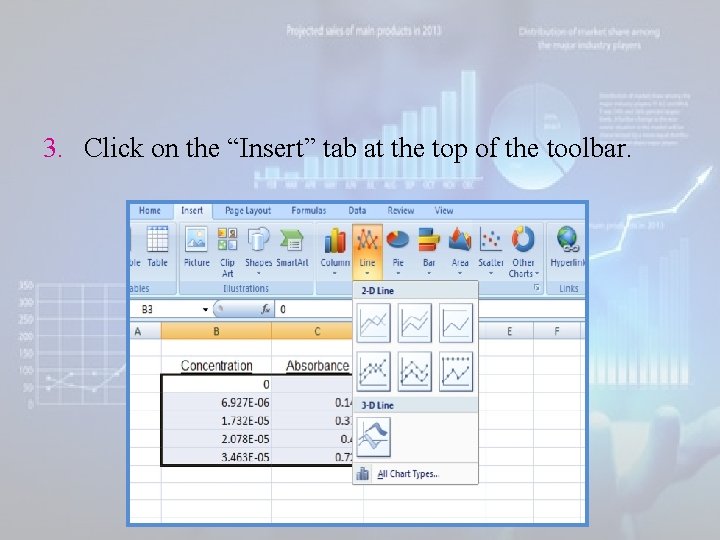
3. Click on the “Insert” tab at the top of the toolbar.

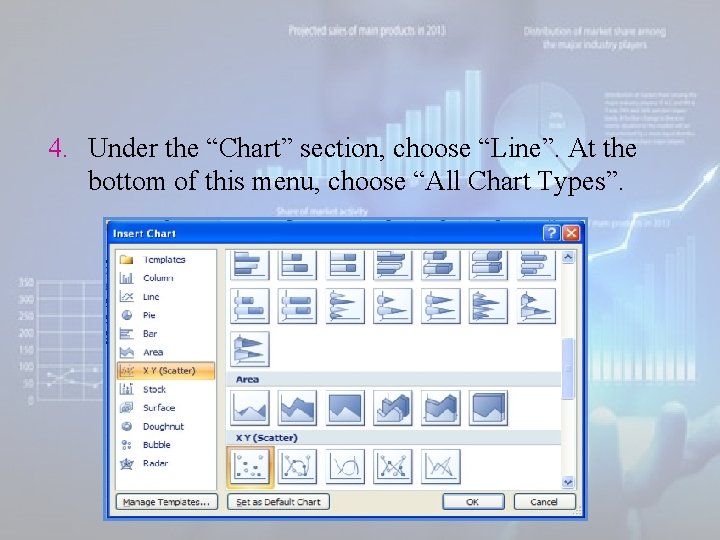
4. Under the “Chart” section, choose “Line”. At the bottom of this menu, choose “All Chart Types”.

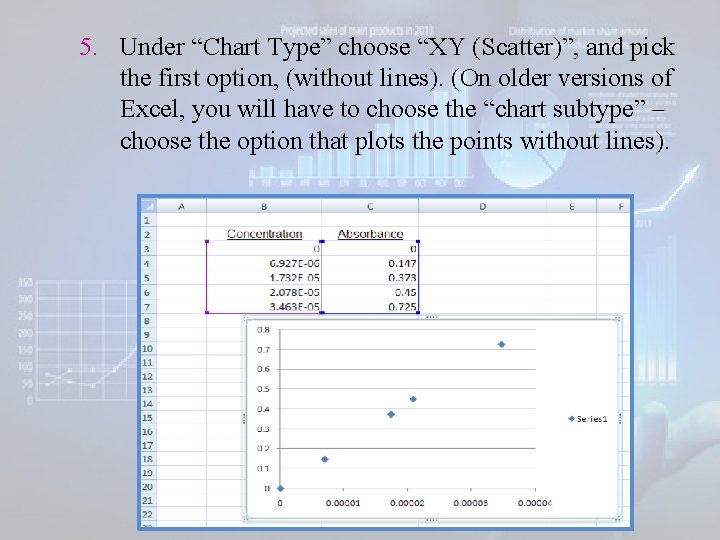
5. Under “Chart Type” choose “XY (Scatter)”, and pick the first option, (without lines). (On older versions of Excel, you will have to choose the “chart subtype” – choose the option that plots the points without lines).

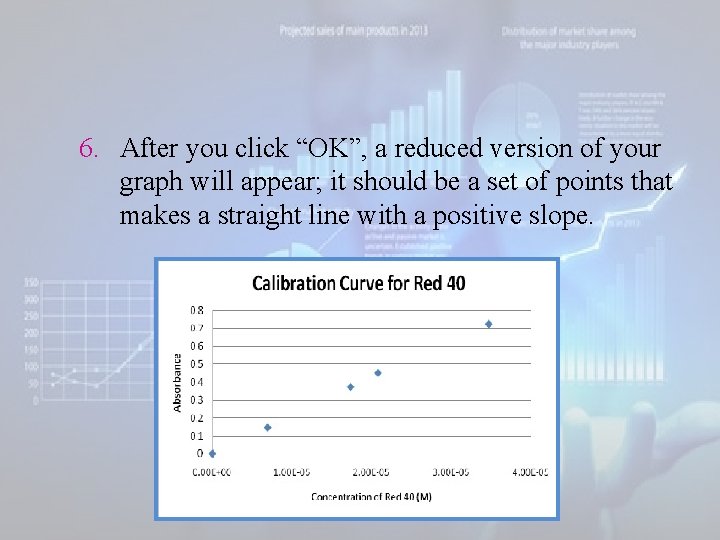
6. After you click “OK”, a reduced version of your graph will appear; it should be a set of points that makes a straight line with a positive slope.

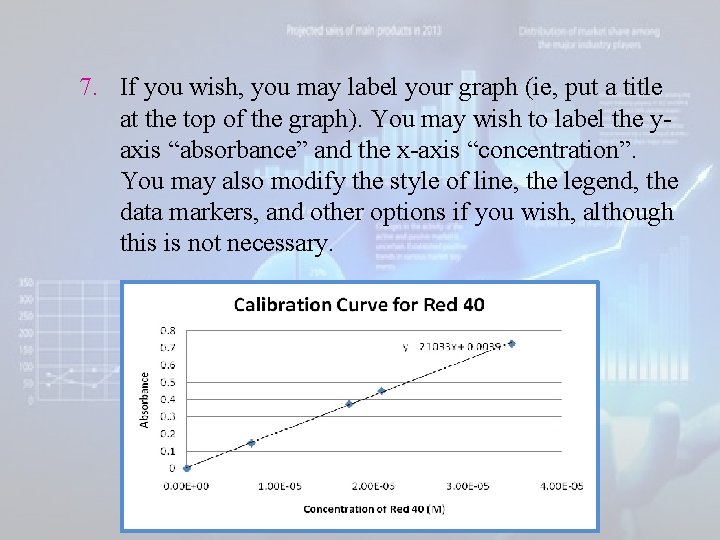
7. If you wish, you may label your graph (ie, put a title at the top of the graph). You may wish to label the yaxis “absorbance” and the x-axis “concentration”. You may also modify the style of line, the legend, the data markers, and other options if you wish, although this is not necessary.

8. Next you want to determine the slope and intercept of your line. Move the mouse cursor to any data point and press the left mouse button. All of the data points should now be highlighted. Now, while the mouse cursor is still on any one of the highlighted data points, press the right mouse button, and click on “Add Trendline” from the menu that appears. 9. From within the "Trendline" window, select the type of “Trend / Regression Type” you want – for a Beer’s Law plot the function should be “Linear”.

10. Click “OK”. A line and an equation should appear on the graph, as shown below. Notice that this equation is in the format {y = mx + b}, and numerical values are provided for the slope and intercept. The value of the intercept should be close to zero, a small number, but it may not be exactly zero. In my example, the slope is 21033 and the intercept is 0. 0039. The data points may be difficult to see on the standard axes that Graph provides. To zoom in on the data, select the menu “Zoom” and click on the choice “Fit”; this will rescale your graph so that all the data points fit nicely on the screen and can be easily read. Now you want to determine the slope and intercept of your line. Select the “Function” menu and click on the choice “Insert Trendline”.

• Several choices will appear (linear, logarithmic, polynomial, exponential, etc. ); choose the “linear” fit and click “OK”. When your graph reappears, you will see a line that fits your data, and the function appears in the upper left corner of the screen, like this: f(x) = mx + b where, of course, m is the slope and b is the intercept. The program will provide numerical values for m and b; the value of the intercept should be close to zero, a small number, but it may not be exactly zero. You may print the graph, or save it as a bitmap or jpg image, by selecting the appropriate choice from the “File” menu.

• You may also save the data set, from the “File” menu, so you can recall it later without entering the numbers again. Using a graphing calculator to plot calibration curve: Almost all scientific calculators (e. g. TI-83, TI-84, TI-89) will calculate slopes and y-intercepts for linear data sets. Please note that you don’t necessarily need a graphing calculator; almost any scientific calculator will calculate slope and intercept for a data set of x, y data. Refer to the documentation for your calculator if you want to determine your slope and intercept directly, using your calculator. (This will require you to plot and print the calibration curve separately).

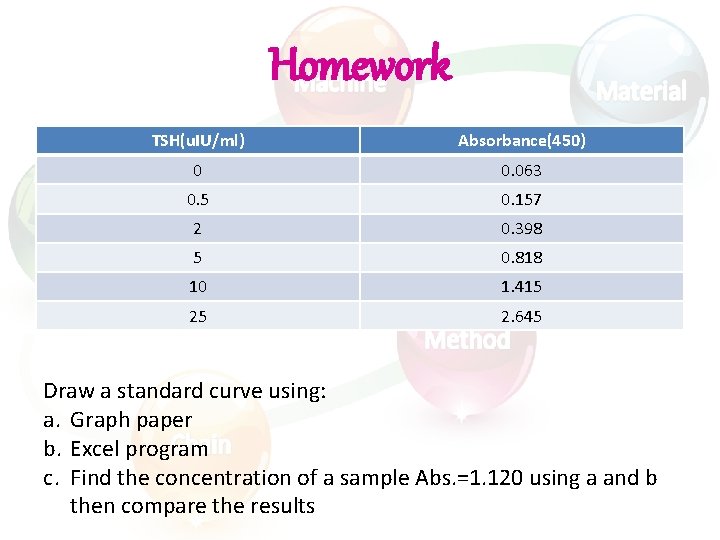
Homework TSH(u. IU/ml) Absorbance(450) 0 0. 063 0. 5 0. 157 2 0. 398 5 0. 818 10 1. 415 25 2. 645 Draw a standard curve using: a. Graph paper b. Excel program c. Find the concentration of a sample Abs. =1. 120 using a and b then compare the results

Definition of Terms • Accuracy: The degree to which the measured concentration corresponds to the true concentration of a substance. This is related in part to the specificity of the assay. • Precision: Refers to the repeatability of a measured value or the consistency of results. It is a measure of random error defined as the variation among replicate measurements of a defined sample. It is expressed as the Coefficient of Variation (%CV) which is the(Standard Deviation/Mean)*100.

• Sensitivity: method sensitivity refers simply the lowest level of analyte that can be detected by a given method with low CVs. • Specificity: refers to how specific a test is for a certain substance without interferences. • Bias: the difference between the true value and value obtained. • Concentration: a measure of the amount of dissolved substance per unit of volume. • Lyophilized: freeze-dried. • Reproducibility: Reproducibility of results can be assessed by calculating CV values to compare mean concentrations. to

• Analyte: the constituent or characteristic of the sample to be measured. • Assay: to analyze a sample of a specimen to determine the amount, activity, or potency of a specific analyte or substance. • Out of control: indicates that the analysis of patient samples is unreliable. • Run: a period to time or series of measurements within which accuracy and precision of the measuring system are expected to be stable. • Range: the difference between the largest and smallest observed value of a quantitative characteristic or statistical limits.

Thank You