Quali sono le necessit della Crittografia moderna o
























- Slides: 24


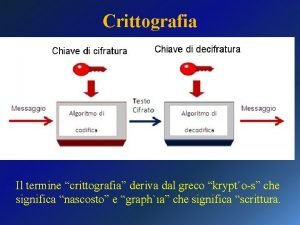
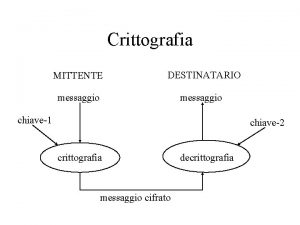
Quali sono le necessità della Crittografia moderna o Crittografìa a chiave pubblica? • Non deve essere richiesto nessuno scambio di chiave • Decifrare deve essere un'operazione enormemente più difficile che cifrare, a meno che non si disponga di ulteriori informazioni specifiche

La Matematica sa fornire idee e strumenti per rispondere alle esigenze della Crittografia moderna Sono i settori della Matematica come l’ Informatica Teorica che hanno offerto numerosi spunti e fonti di ispirazione per la costruzione di funzioni a senso unico e quindi di criptosistemi a chiave pubblica

Un’idea per soddisfare queste esigenze potrebbe essere quella di usare funzioni a senso unico: • funzioni di cifratura che siano facilmente computabili (in modo che chiunque possa velocemente criptare un messaggio per un dato utente A) • siano invertibili (in modo da permettere la decifratura) • abbiano un'inversa il cui calcolo è proibitivo in assen - za di ulteriori informazioni (che costituiscono la chiave privata di A, che solo A deve conoscere e senza la quale nessun pirata potrà infrangere in tempi rapidi un messaggio eventualmente intercettato)

Niente assicura che simili funzioni esistano La difficoltà di calcolare l'inversa potrebbe essere soltanto transitoria e passeggera, legata allo stato attuale delle conoscenze scientifiche

Ad una famosa questione di Informatica Teorica e ad alcune sue applicazioni alla Teoria dei Numeri è legata parte della Crittografia moderna P = NP ? {problemi che hanno un algoritmo P = di soluzione rapido} {problemi che ammettono un algoritmo NP = rapido di verifica delle soluzioni} Quindi P = NP domanda se tutti i problemi che ammettono un procedimento rapido di verifica delle soluzioni hanno anche un algoritmo veloce di soluzione

Una questione di cui si cerca, se esiste, la soluzione Un problema matematico, o comunque riconducibile a un modello matematico, si deve esprimere nel linguaggio matematico, che si compone di simboli specifici come le cifre decimali 0, 1, 2, …, 8, 9 oppure le lettere x, y, z, . . . Quei simboli matematici necessari a esprimere il contesto di un particolare problema formano l'alfabeto di quel problema

Consiste nel riconoscere, tra tutte le sequenze finite di simboli (o parole) del suo alfabeto, quelle che soddisfano una prefissata condizione ESEMPIO: Stabilire se un dato numero naturale N 2 è primo Consiste nel calcolare, per ogni parola dell'alfabeto, la sua immagine in una qualche funzione ESEMPIO: Per ogni naturale N 2 composto, decomporre N nei suoi fattori primi

Insieme S di parole su un alfabeto finito A La questione da risolvere è per ogni parola w su A, se w è in S o no (per ogni naturale N 2, si vuole decidere se N è primo o no) calcolare la sua immagine in una determinata funzione (per ogni naturale N 2, si vuole determinare la sequenza dei fattori primi di N)

Si chiama algoritmo una successione finita di istruzioni, seguendo le quali, sui dati assegnati (input), si possono eseguire le operazioni che producono i risultati (output) L’algoritmo tratta parole sull’alfabeto (finito) del problema e porta a scegliere quelle che soddisfano determinate condizioni, oppure a calcolare la loro immagine in determinate funzioni Per certi problemi la procedura risolutiva si trova facilmente, per altri si raggiunge con maggior difficoltà, per altri ancora resta incerta e misteriosa: anzi, in questi ultimi casi si può addirittura dubitare che un algoritmo di soluzione si possa realmente scoprire

Come possiamo allora sviluppare un trattamento astratto uniforme di queste situazioni così diverse? Come possiamo dare una definizione teorica generale di esistenza di un algoritmo? Tesi di Turing: Turing Un problema ha un "algoritmo" che lo risolve se e solo se c'è una Macchina di Turing che è capace di farlo Se accettiamo la Tesi di Turing, disponiamo di una precisa identificazione dei problemi che hanno procedimento di soluzione

L’esistenza di un procedimento che fornisce le risposte di un problema, talvolta, non è sufficiente a garantire una trattazione adeguata e soddisfacente del problema stesso Bisogna caratterizzare la nozione di algoritmo rapido e stabilire quali problemi hanno un procedimento rapido di risposta e quali no Tesi di Edmonds – Cook - Karp: Un algoritmo è efficiente (= rapido) se e solo se lavora in tempo al più polinomiale rispetto alla lunghezza dell'input

Ø P NP perché ogni algoritmo rapido di soluzione costituisce implicitamente anche una verifica Ø Se P NP esistono problemi i cui tempi di soluzione sono significativamente più lunghi di quelli di verifica, ovvero esistano problemi privi di un algoritmo rapido di dimostrazione ma dotati di un algoritmo veloce di verifica Ø Ci sono forti argomenti che sembrano avvalorare la congettura negativa P NP

Ø Un problema S si dice NP-completo se a) S ammette un algoritmo rapido di verifica, e dunque sta in NP b) ogni problema S' in NP si può ricondurre a S in tempo polinomiale Ø Un problema S si dice NP- intermedio se appartiene allo spazio in NP P Ø Tornando alla crittografia, la disparità di tempo tra gli algoritmi di verifica e quelli di soluzione di un problema NP- completo o NP- intermedio può fornire spunti per la costruzione di funzioni F a senso unico: - legare la computazione di F (codifica del criptosistema) alla procedura (rapida) di verifica - legare la computazione dell'inversa di F (decodifica) alla difficoltà di ottenere algoritmi veloci di soluzione

Un'altra copiosa fonte di ispirazione per le funzioni a senso unico è la Teoria dei Numeri Naturali Il sistema RSA si basa sostanzialmente sulla differenza che attualmente si rileva tra i tempi di soluzione di due famosi problemi sui naturali: (a) riconoscere i numeri primi, (b) decomporre un numero composto nei suoi fattori primi Ø Si sa che (a) appartiene a P Ø Si congettura che (b) sia NP- intermedio, comunque sta in NP e non è nota alcuna procedura classica che lo sappia risolvere in tempo rapido

Il Problema della Primalità chiede di determinare un algoritmo che sappia decidere, per ogni intero positivo N 2, (dispari) se N è primo oppure no Capaci di raggiungere la risposta corretta in modo diretto e privo di dubbi ed errori in un numero finito di passi Procedimenti di decisione che ammettono errori, purché di bassa probabilità, cioè si accetta di sacrificare la precisione pur di accelerare i tempi di lavoro

Algoritmo elementare di primalità (noto agli antichi Greci) Consiste nel considerare ogni numero naturale (anzi primo) a da 2 a N e verificare se a divide oppure no N; Ø se la divisione per un qualche a è precisa (cioè dà resto nullo), allora N è composto, ed a è un suo divisore; Ø se nessuna divisione si dimostra esatta, N è primo Crivello di Eratostene Consiste nel determinare i numeri primi N: Ø Ø Ø si scrivono i numeri da 2 a N, disposti su righe; si segna 2 e si cancellano i suoi multipli > 2; si segna il minimo sopravvissuto 3 e si cancellano i suoi multipli > 3; si segna il minimo sopravvissuto 5 e si cancellano i suoi multipli > 5; si prosegue fino a superare √N; I numeri sopravvissuti sono i primi N. N è primo se è uno di loro

Nel 1801 Gauss scriveva così del problema di primalità: "dobbiamo confessare che tutti i metodi che sono stati proposti finora si restringono a casi molto speciali, oppure sono talmente faticosi e prolissi da non applicarsi ai numeri più grandi" Quello che si cerca non è tanto un algoritmo di primalità, quanto piuttosto un procedimento che risolva il problema lavorando in tempo rapido (cioè polinorniale rispetto alla lunghezza dell'input N, ovvero rispetto al logaritmo di N) Il procedimento elementare dei Greci non è utile nella pratica: può richiedere troppe divisioni (un numero comparabile a N) e dunque tempi proibitivi (esponenziali) prima di dare la risposta La ricerca di un algoritmo efficiente di primalità ha richiesto altri due secoli di lavoro dal tempo di Gauss, non è stata facile e si è conclusa solo nel 2002, quando i tre ricercatori indiani Agrawal, Kayal e Saxena sono riusciti a mettere a punto un procedimento (denominato AKS dalle loro iniziali) che risolve il problema della primalità di N in tempo al più polinomiale nella lunghezza di N

Hanno la seguente caratteristica: su ogni input N danno la loro risposta, magari scorretta, fornendo comunque la probabilità di errore. Risposte probabilmente vere in tempi certamente rapidi Hanno la seguente caratteristica: la risposta a un dato input N, quando arriva, è sempre corretta, ma è ammessa la facoltà di non rispondere Risposte certamente vere in tempi probabilmente rapidi

L'algoritmo probabilistico più famoso (ed adoperato) è quello di Miller e Rabin È un algoritmo probabilistico di tipo Montecarlo, che risolve il problema di primalità in tempo polinomiale con una possibilità di errore relativamente trascurabile L’algoritmo di Miller - Rabin si dimostra: Ø pienamente affidabile quando dichiara un numero N COMPOSTO Ø fallibile altrimenti

Si basa sul Piccolo Teorema di Fermat, combinato con l'osservazione che, per , N primo (dispari), la congruenza x 2 1 (mod N) ha le due uniche soluzioni x 1 (mod N) Sia N un primo dispari. Sia poi a un intero primo con N, allora si ha Ma N - 1 è pari, quindi possiamo scrivere N 1 = 2 s t con s e t naturali opportuni, s positivo e t dispari e ottenere:

da cui deriviamo Se poi abbiamo e anche è pari (cioè s 2), quindi e si può ripetere ancora il ragionamento. In generale, ripercorrendo a ritroso modulo N, le potenze di a • incontriamo 1 • oppure concludiamo at 1 (mod. N)

Sulla base delle precedenti considerazioni, organizziamo il test probabilistico di primalità di Miller-Rabin Sia N un intero dispari > 2. Poniamo N 1 = 2 s t per s, t naturali, s e t dispari. Scegliamo un intero a con 1 < a < N e calcoliamo prima (a, N) e poi, se necessario, le potenze modulo N (per r < s naturale) • Se (a, N) 1, dichiariamo N COMPOSTO • Se (a, N) = 1 ma a. N l ≡ 1 (mod N), dichiariamo N COMPOSTO • Se (a, N) = 1, a. N l 1 (mod N) ma at ≡ 1 (mod N) e, per ogni naturale r < s, (mod. N), dichiariamo N COMPOSTO • Se (a, N) = 1, a. N l 1 (mod. N) e at 1 (mod. N) oppure, per qualche naturale r < s, (mod. N), dichiariamo N PROBABILMENTE PRIMO

PROPOSTE DI LAVORO 1. Dimostrazione della variante al piccolo teorema di Fermat: N primo, a intero primo con N a. N-1 1 (mod N) 2. Dimostrare che per N primo x 2 1 (mod N) x ± 1 (mod N) 3. Se a primo con N e a. N-1 1 (mod N) N primo ? 4. (Es. N=341, N=561) 4. Applichiamo l’algoritmo di Miller-Rabin a N=29 e N=341
 Quali sono i paradigmi della comunicazione
Quali sono i paradigmi della comunicazione Elementi costitutivi del testo narrativo
Elementi costitutivi del testo narrativo Storia della crittografia
Storia della crittografia Necessit
Necessit Le macchine semplici mappa concettuale
Le macchine semplici mappa concettuale Tipi di giurisdizione
Tipi di giurisdizione I 5 regni viventi
I 5 regni viventi Quali sono le sostanze pure
Quali sono le sostanze pure Insetto con chele
Insetto con chele Le piante spermatofite
Le piante spermatofite Scheletro vertebrati
Scheletro vertebrati I solidi di rotazione
I solidi di rotazione I glucidi sono detti anche
I glucidi sono detti anche Stile cognitivo verbale analitico
Stile cognitivo verbale analitico Differenza tra forze endogene e esogene
Differenza tra forze endogene e esogene Pronomi relativi indefiniti
Pronomi relativi indefiniti Quali sono i sette sacramenti
Quali sono i sette sacramenti Quali sono le fasi del salto in lungo
Quali sono le fasi del salto in lungo Esempi di facilitatori
Esempi di facilitatori Quali sono gli elementi fondamentali di uno stato
Quali sono gli elementi fondamentali di uno stato Organi di garanzia costituzionale
Organi di garanzia costituzionale Uovo dittongo o iato
Uovo dittongo o iato Fasi del ciclo cliente in albergo
Fasi del ciclo cliente in albergo Che cosa sono i numeri interi
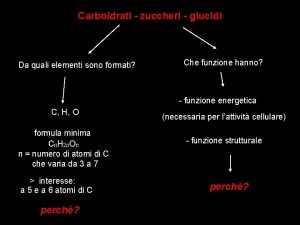
Che cosa sono i numeri interi Carboidrati funzione
Carboidrati funzione