Quadrats ANOVA Quadrat shape 1 Edge effects worst










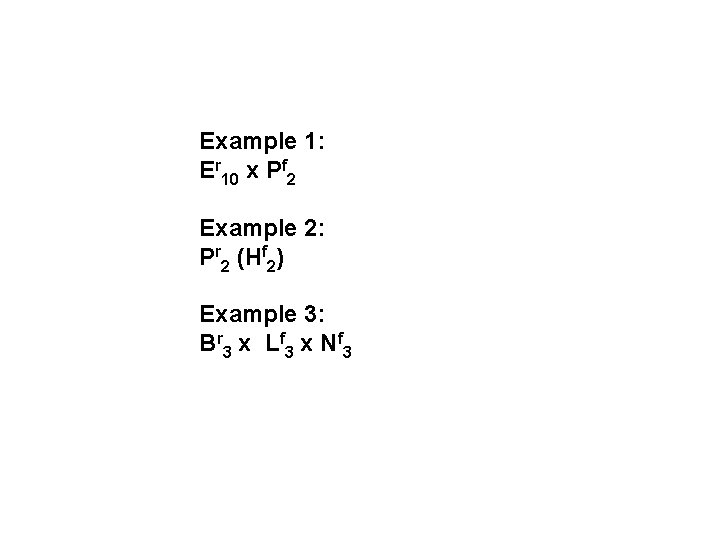
- Slides: 21

Quadrats, ANOVA

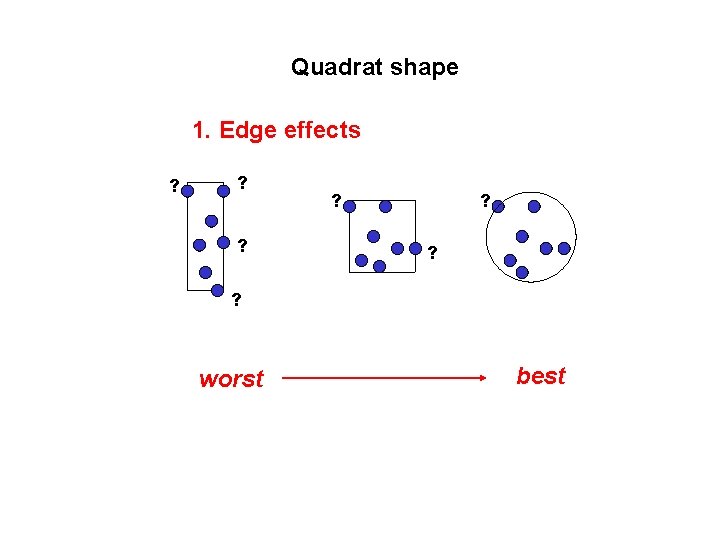
Quadrat shape 1. Edge effects ? ? worst best

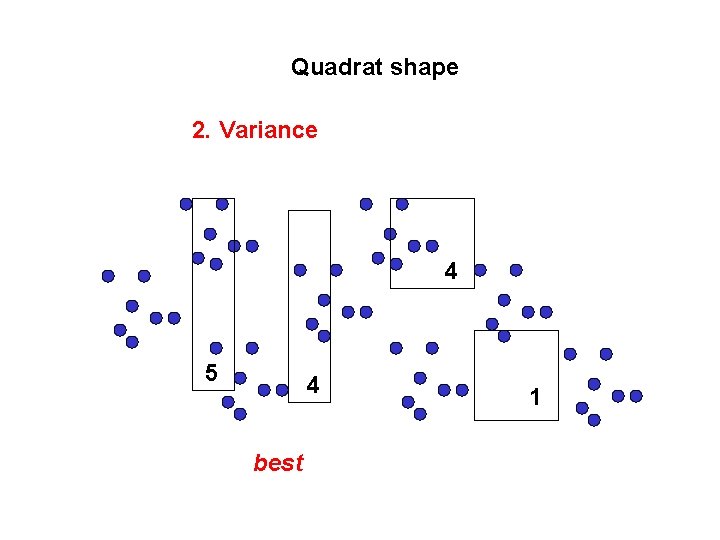
Quadrat shape 2. Variance 4 5 4 best 1

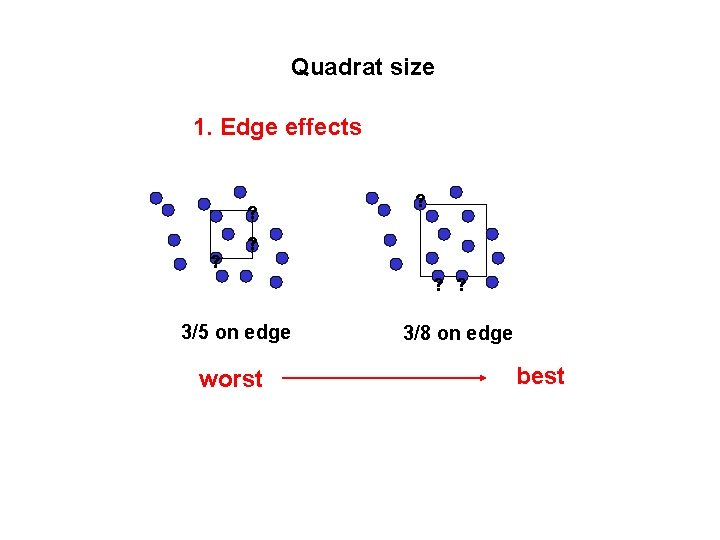
Quadrat size 1. Edge effects ? ? ? ? ? ? 3/5 on edge worst 3/8 on edge best

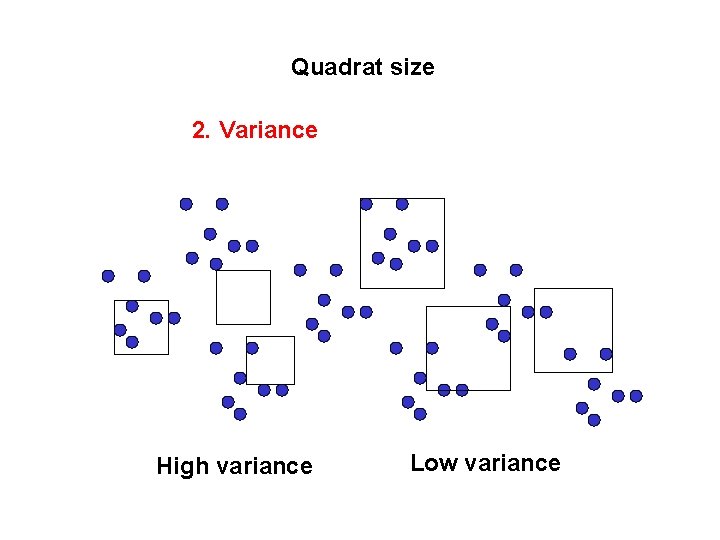
Quadrat size 2. Variance High variance Low variance

Quadrat size So should we always use as large a quadrat as possible? Tradeoff with cost (bigger quadrats take l o n g e r to sample)

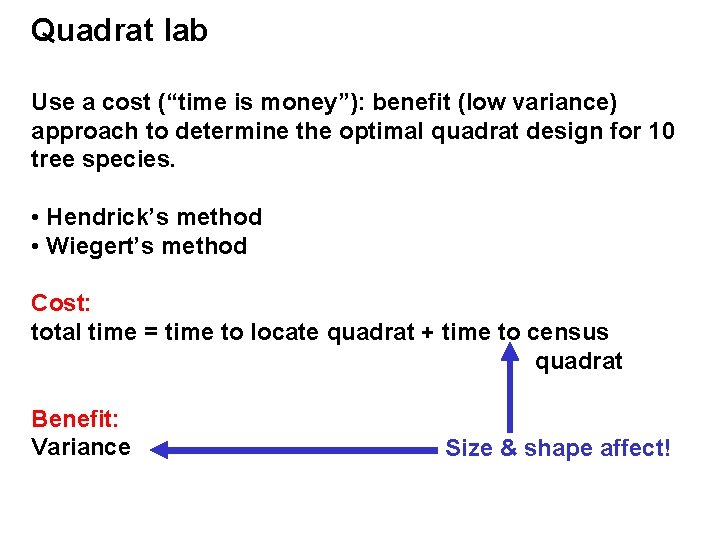
Quadrat lab Use a cost (“time is money”): benefit (low variance) approach to determine the optimal quadrat design for 10 tree species. • Hendrick’s method • Wiegert’s method Cost: total time = time to locate quadrat + time to census quadrat Benefit: Variance Size & shape affect!

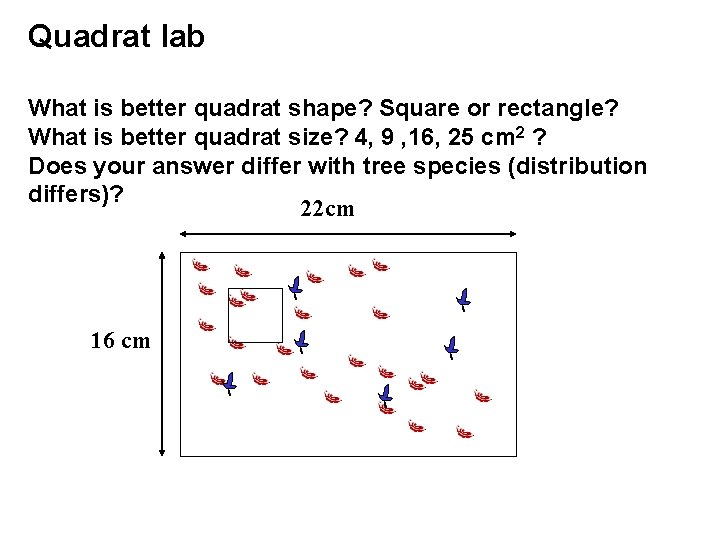
Quadrat lab What is better quadrat shape? Square or rectangle? What is better quadrat size? 4, 9 , 16, 25 cm 2 ? Does your answer differ with tree species (distribution differs)? 22 cm 16 cm

ANOVA Example: formal notation Example 1 Ecologists: Er 10 Papers: Pf 2 Example 2: Populations: Pr 2 Herbivory: Hf 2 Example 3: Light: Lf 3 Nutrients: Nf 3 Blocks: Br 3

Fixed-effects ANOVA (Model I) • All factors are fixed Random-effects ANOVA (Model II) • All factors are random Mixed-model ANOVA (Model III) • Contains both fixed and random effects, e. g. randomized block!

Two-way factorial ANOVA How to calculate “F” Fixed effect (factors A & B fixed) Random effect (factors A & B random) Mixed model (A fixed, B random) Factor A MS Error MS A x B Factor B MS Error MS B MS A x B MS Error Ax. B MS A x B MS Error

Factorial design: All levels of one factor crossed by all levels of another factor, i. e. all possible combinations are represented. If you can fill in a table with unique replicates, it’s factorial! Ambient CO 2 Double CO 2 Pea plant Bean plant Corn plant

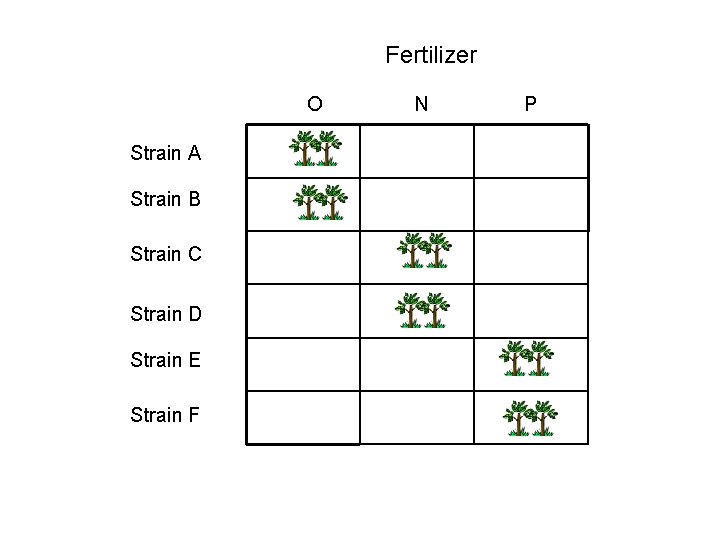
Nested design In this example, strain type is “nested within” fertilizer. Fertilizer is often called “group”, strain “subgroup” The nested factor is always random No fertilizer Strain A Strain B Nitrogen fertilizer Strain C Strain D Phosphorus fertilizer Strain E Strain F

Fertilizer O Strain A Strain B Strain C Strain D Strain E Strain F N P

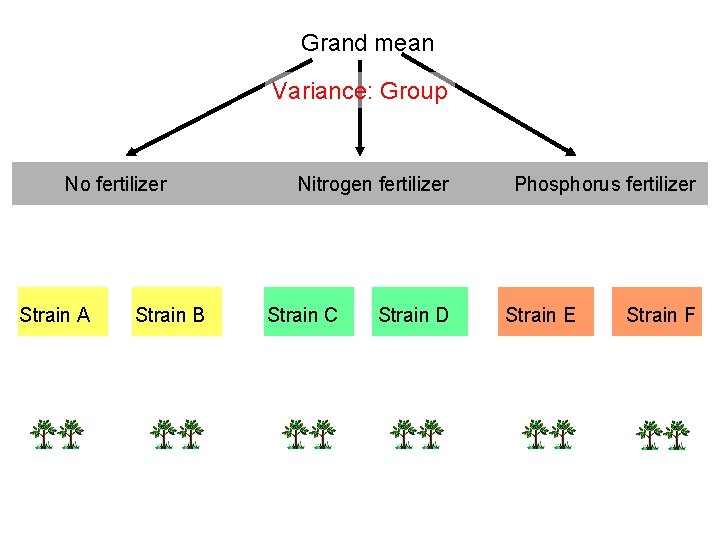
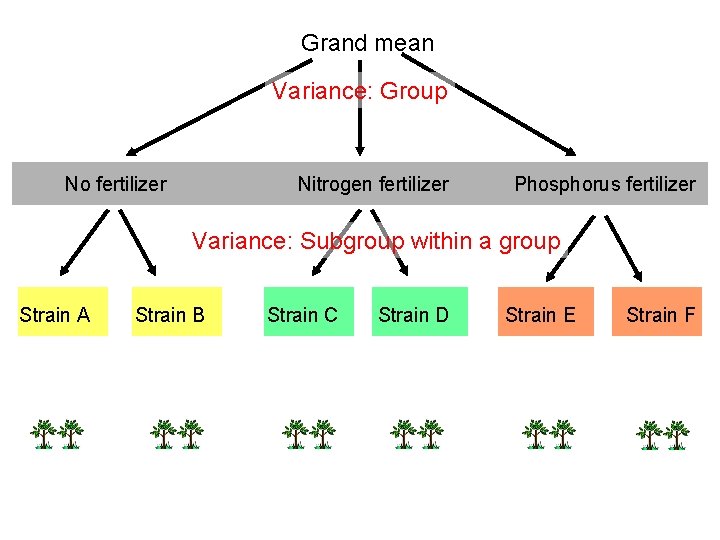
Grand mean Variance: Group No fertilizer Strain A Strain B Nitrogen fertilizer Strain C Strain D Phosphorus fertilizer Strain E Strain F

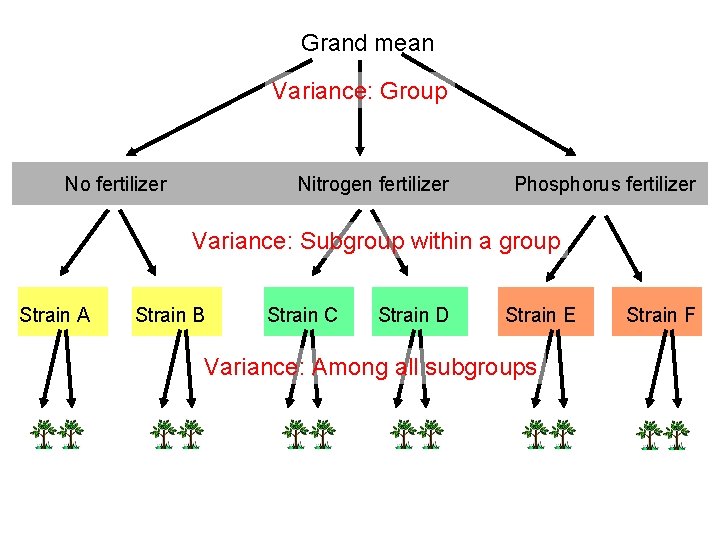
Grand mean Variance: Group No fertilizer Nitrogen fertilizer Phosphorus fertilizer Variance: Subgroup within a group Strain A Strain B Strain C Strain D Strain E Strain F

Grand mean Variance: Group No fertilizer Nitrogen fertilizer Phosphorus fertilizer Variance: Subgroup within a group Strain A Strain B Strain C Strain D Strain E Variance: Among all subgroups Strain F

Nested ANOVA: “A” Subgroups nested within “B” Groups, with n replicates In our example, A=2, B=3 and n=2 df F Groups B-1 MS Groups MS Subgroups within groups B(A-1) MS Subgroups within groups MS Among all subgroups AB(n-1) Total ABn-1

Formal notation cont. Af 6 x Br 5 tells us that this is a factorial design with factor A “crossed” with factor B Af 6 (Br 5) tells us that this is a nested design with factor A “nested within” with factor B. In other words, A is subgroup, B is group.

Group exercise (groups of 3) Experimental design handout Ø Write out the factors and levels using formal notation
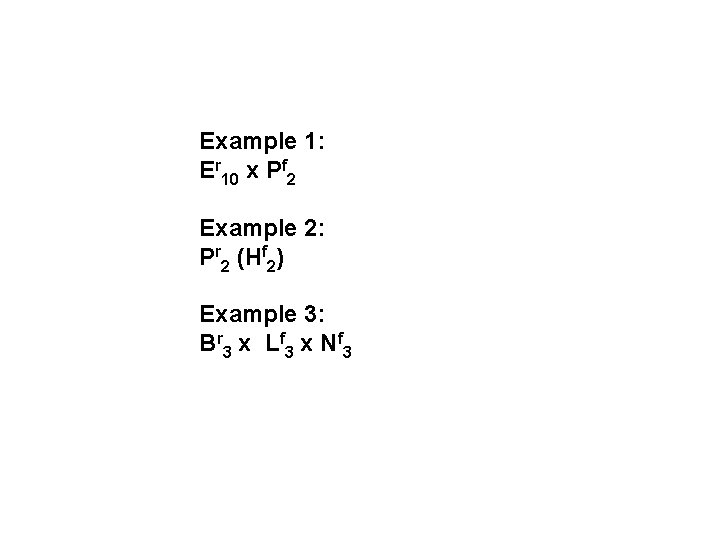
Example 1: Er 10 x Pf 2 Example 2: Pr 2 (Hf 2) Example 3: B r 3 x L f 3 x N f 3