QUADRATICS THE MATH OF NUMBERS CREATED BY CHARLOTTE

QUADRATICS: THE MATH OF NUMBERS ✎ CREATED BY CHARLOTTE, JOY, RACHEL, AND PARKER

THE FORMULA……✄

FACTORING ☜☞

HOW TO FACTOR • Set up an X • Put b on the top and c on the bottom • Find 2 numbers that add and equal b • And when they multiply, they equal c

FACTORING THROUGH THE FORMULA ✰

DISCRIMINANT ◈ v The discriminant is the equation inside the square root brackets v The discriminant tells us how many solutions we can get v A negative discriminant means no solutions v A positive discriminant means two solutions v If the discriminant equals 0, this means one solution

TRANSLATIONS OF QUADRATICS ☟ • Y= a(x-h)^2 +k • -h shifts right, +h shifts left • When k is positive it shifts up, and when its negative it shifts down • 0< |a|>1 it compresses vertically • |a|>1 it stretches vertically • When a is negative, it is reflected across the x axis

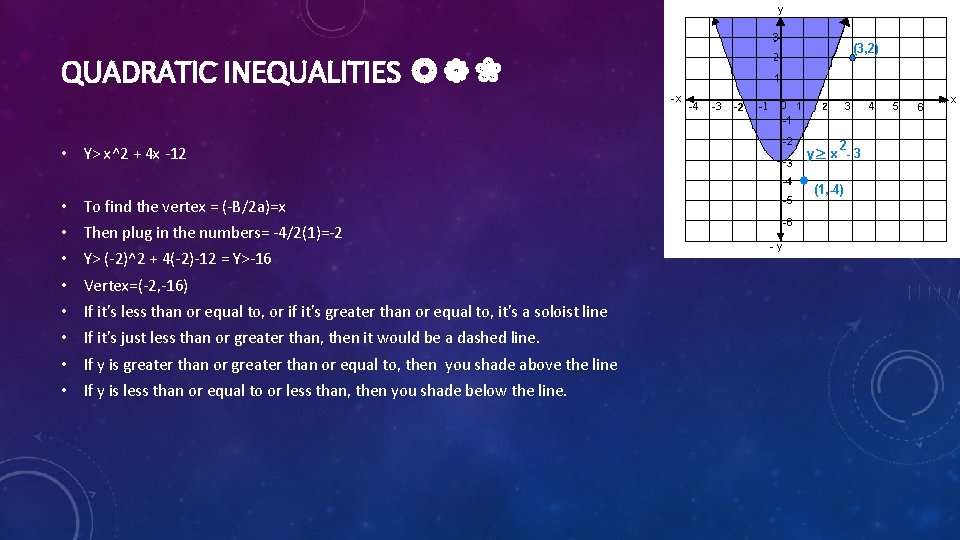
QUADRATIC INEQUALITIES ❂❁❀ • Y> x^2 + 4 x -12 • To find the vertex = (-B/2 a)=x • Then plug in the numbers= -4/2(1)=-2 • Y> (-2)^2 + 4(-2)-12 = Y>-16 • Vertex=(-2, -16) • If it's less than or equal to, or if it's greater than or equal to, it's a soloist line • If it's just less than or greater than, then it would be a dashed line. • If y is greater than or equal to, then you shade above the line • If y is less than or equal to or less than, then you shade below the line.

Sample problems❃ ❂ Solve for x by factoring. X^2 + 5 x -24 = 0 X^2 - 3 x -28 = 0 X^2 + 3 x = 18

SOLVE USING THE FORMULA ◕ • 9 x^2 -3 x -8 = -10 • 9 x^2 +6 x + 6 = 5 • -2 x^2 -8 x - 14 = -6

SOLVE FOR X. ♛ • X^2 = 81 • X^2 = 25 • X^2 = 64 • X^2 = 36

THE END