Quadratics Review y x 2 Quadratics Review y










- Slides: 27

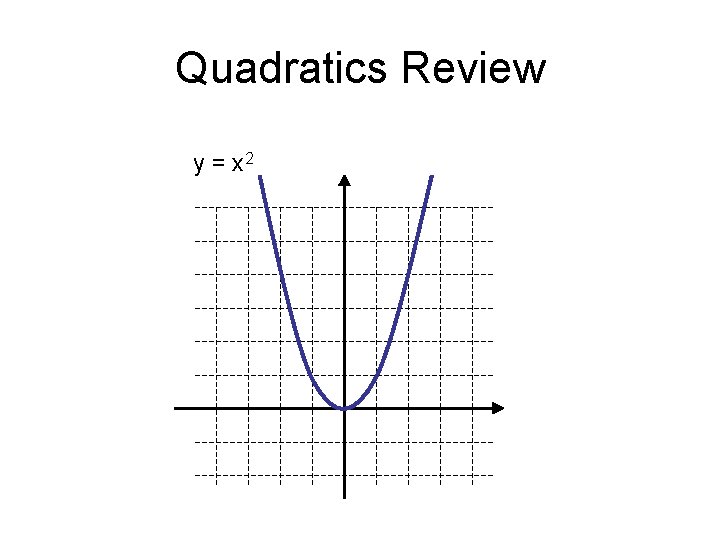
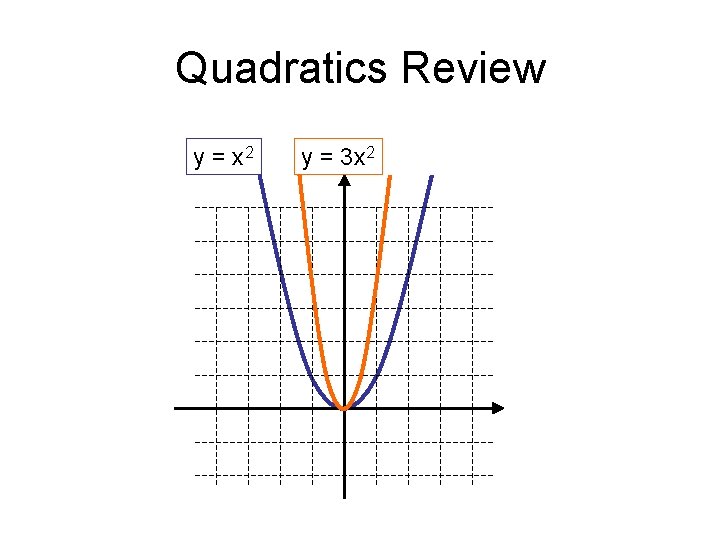
Quadratics Review y = x 2

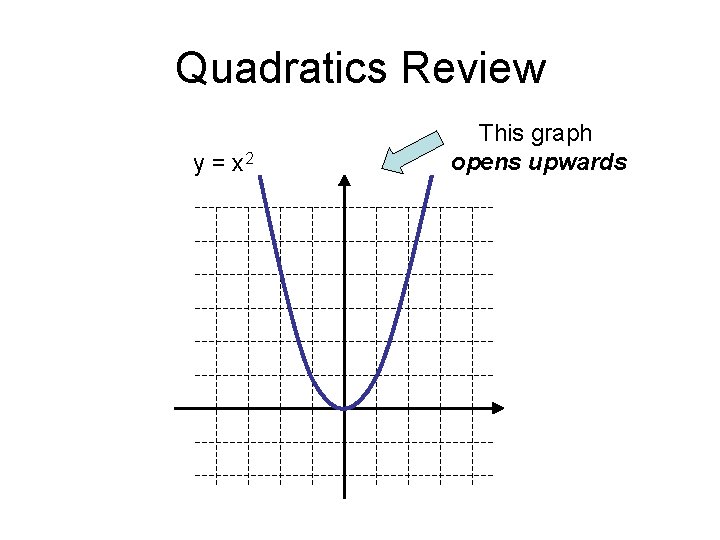
Quadratics Review y = x 2 This graph opens upwards

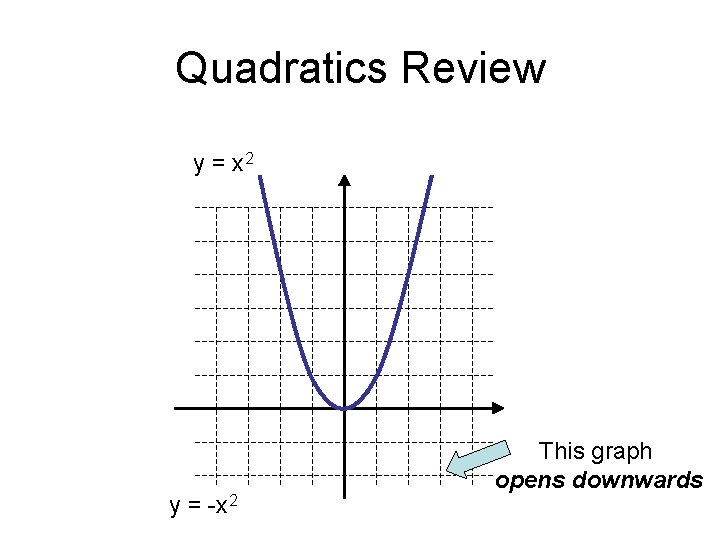
Quadratics Review y = x 2 y = -x 2 This graph opens downwards

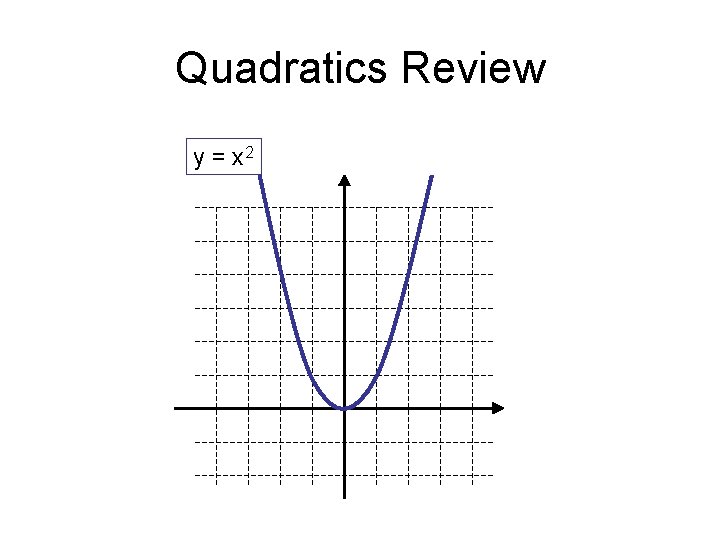
Quadratics Review y = x 2

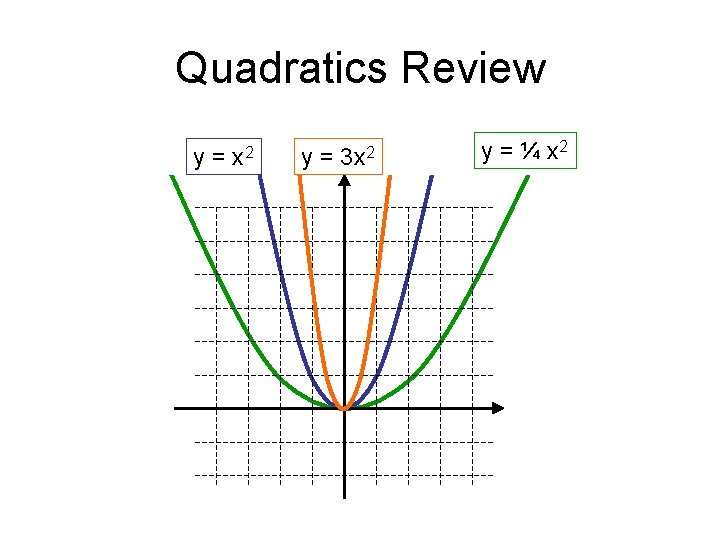
Quadratics Review y = x 2 y = 3 x 2

Quadratics Review y= x 2 y= 3 x 2 y = ¼ x 2

Quadratics Review

Projectile Motion Graphing and manipulating linear and quadratic functions.

Setting up our equations:

Setting up our equations: • In general, we take our initial x-position as x=0

Setting up our equations: • In general, we take our initial x-position as x=0 • And we take GROUND LEVEL as y = 0

Setting up our equations: • In general, we take our initial x-position as x=0 • And we take GROUND LEVEL as y = 0 • This means that our initial yposition is often not zero!

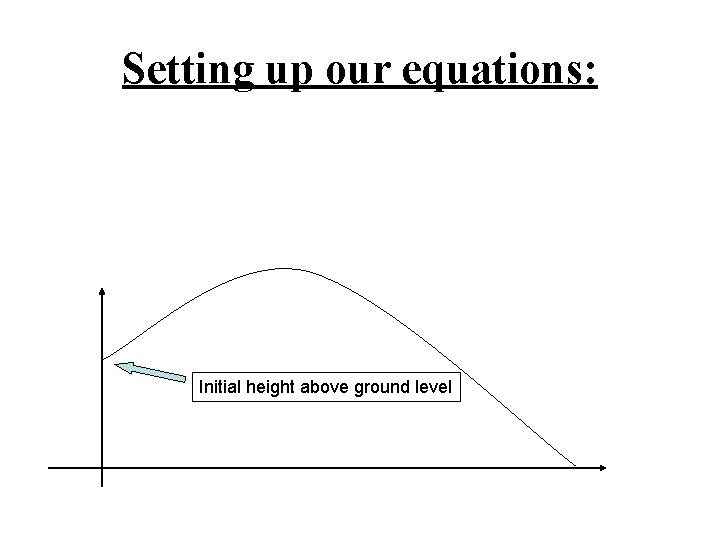
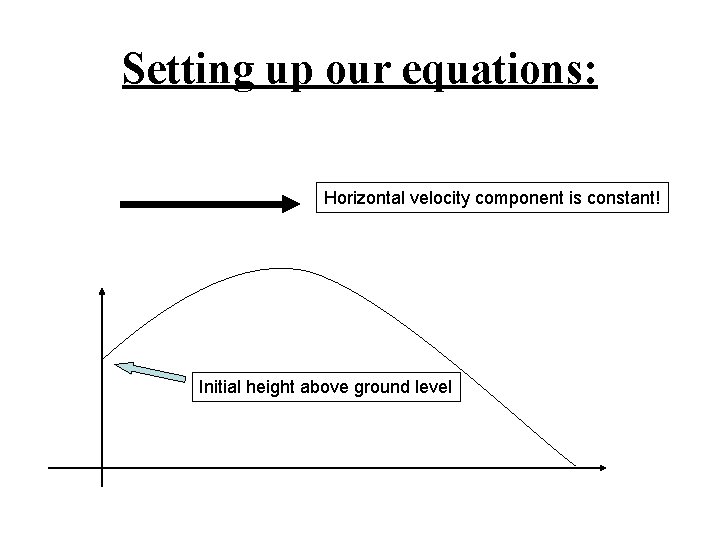
Setting up our equations: Initial height above ground level

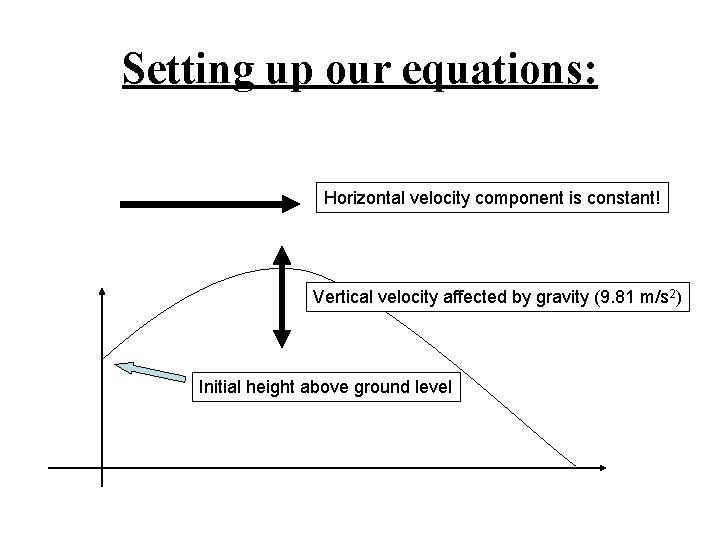
Setting up our equations: Horizontal velocity component is constant! Initial height above ground level

Setting up our equations: Horizontal velocity component is constant! Vertical velocity affected by gravity (9. 81 m/s 2) Initial height above ground level

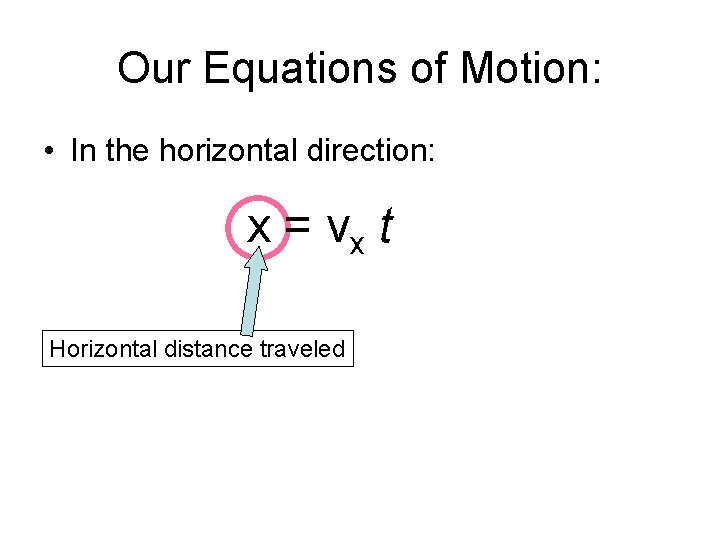
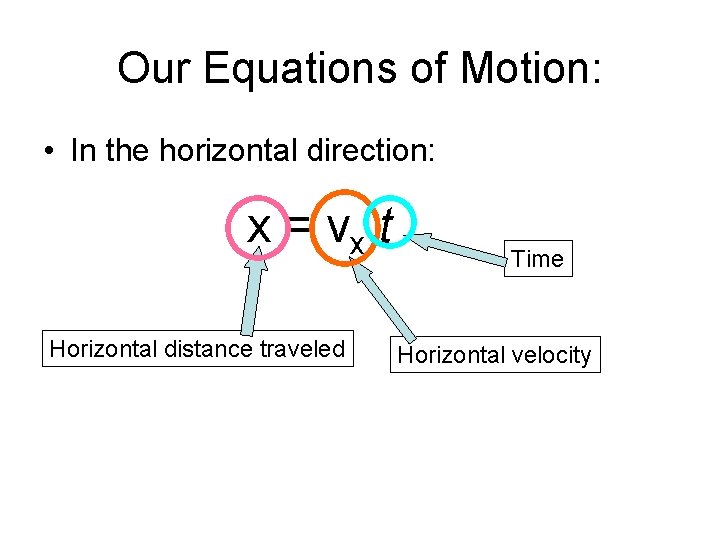
Our Equations of Motion: • In the horizontal direction:

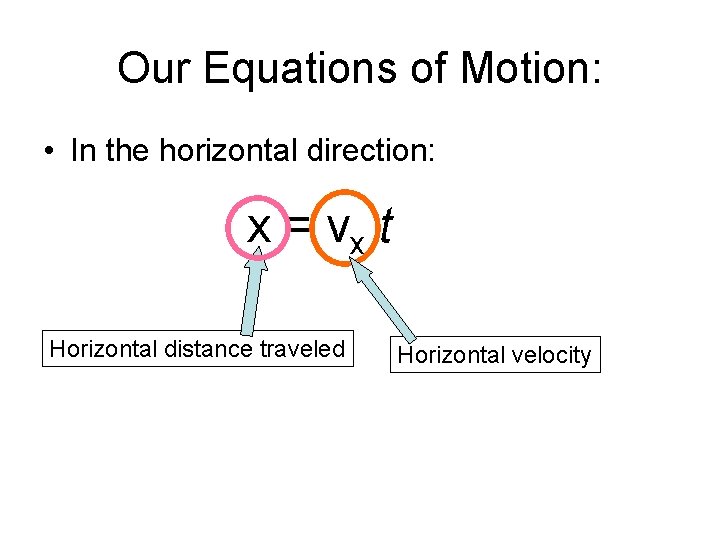
Our Equations of Motion: • In the horizontal direction: x = vx t

Our Equations of Motion: • In the horizontal direction: x = vx t Horizontal distance traveled

Our Equations of Motion: • In the horizontal direction: x = vx t Horizontal distance traveled Horizontal velocity

Our Equations of Motion: • In the horizontal direction: x = vx t Horizontal distance traveled Time Horizontal velocity

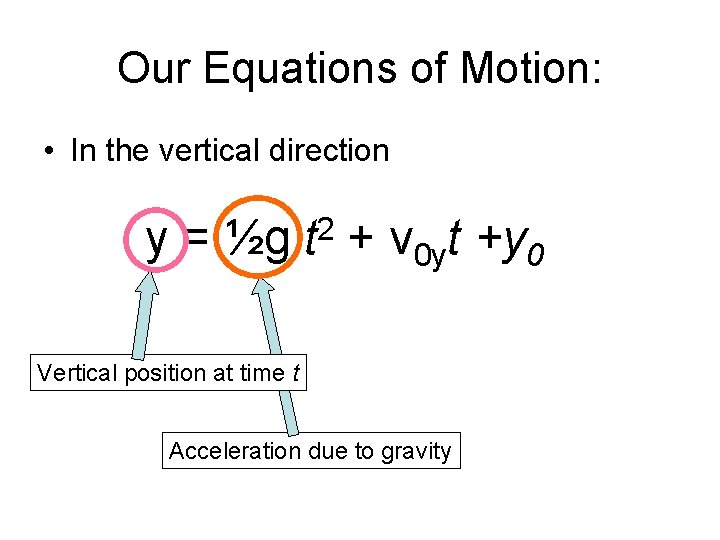
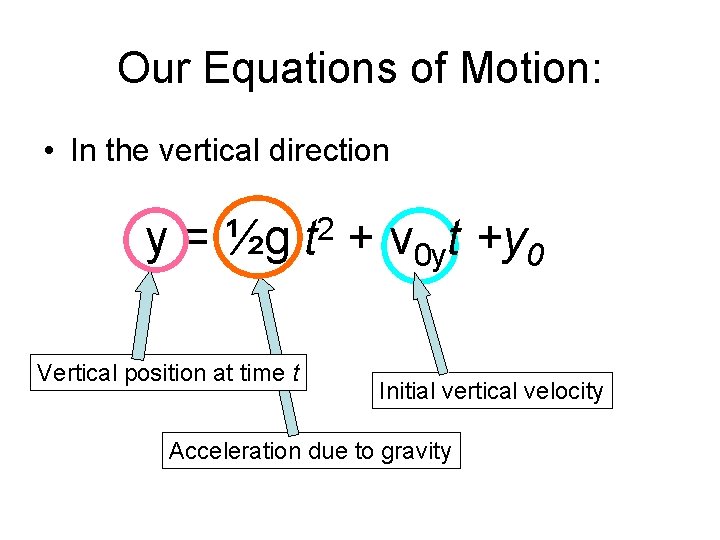
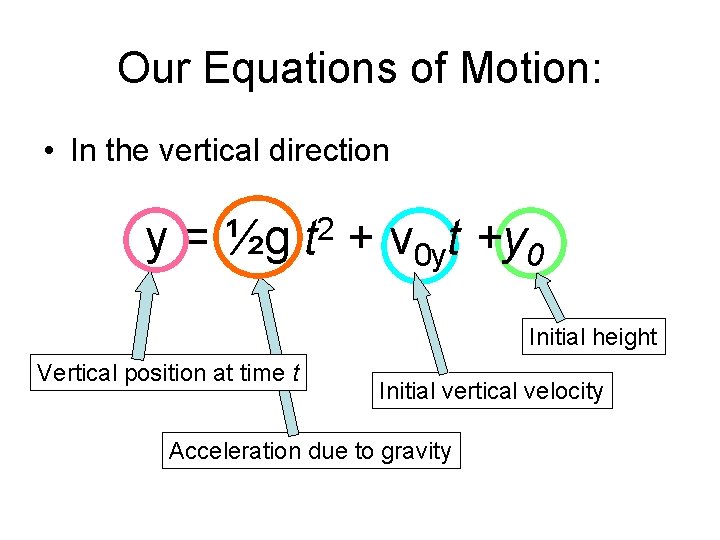
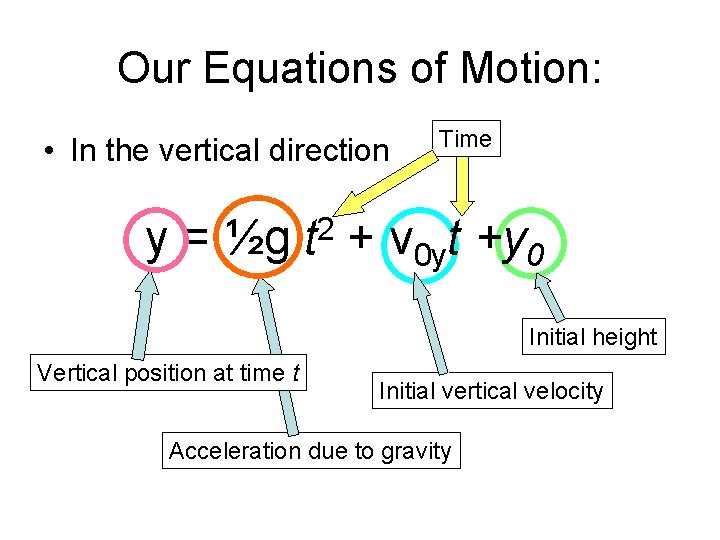
Our Equations of Motion: • In the vertical direction y = ½g 2 t + v 0 yt +y 0

Our Equations of Motion: • In the vertical direction y = ½g Vertical position at time t 2 t + v 0 yt +y 0

Our Equations of Motion: • In the vertical direction y = ½g 2 t + v 0 yt +y 0 Vertical position at time t Acceleration due to gravity

Our Equations of Motion: • In the vertical direction y = ½g Vertical position at time t 2 t + v 0 yt +y 0 Initial vertical velocity Acceleration due to gravity

Our Equations of Motion: • In the vertical direction y = ½g 2 t + v 0 yt +y 0 Initial height Vertical position at time t Initial vertical velocity Acceleration due to gravity

Our Equations of Motion: • In the vertical direction y = ½g 2 t Time + v 0 yt +y 0 Initial height Vertical position at time t Initial vertical velocity Acceleration due to gravity

Our Equations of Motion: • In the horizontal direction x = vx t • In the vertical direction y = ½g 2 t + v 0 yt +y 0 • Because both x and y are defined in terms of another parameter, t, we call these PARAMETRIC EQUATIONS