Quadratics in the Real World Philip is standing

Quadratics in the Real World

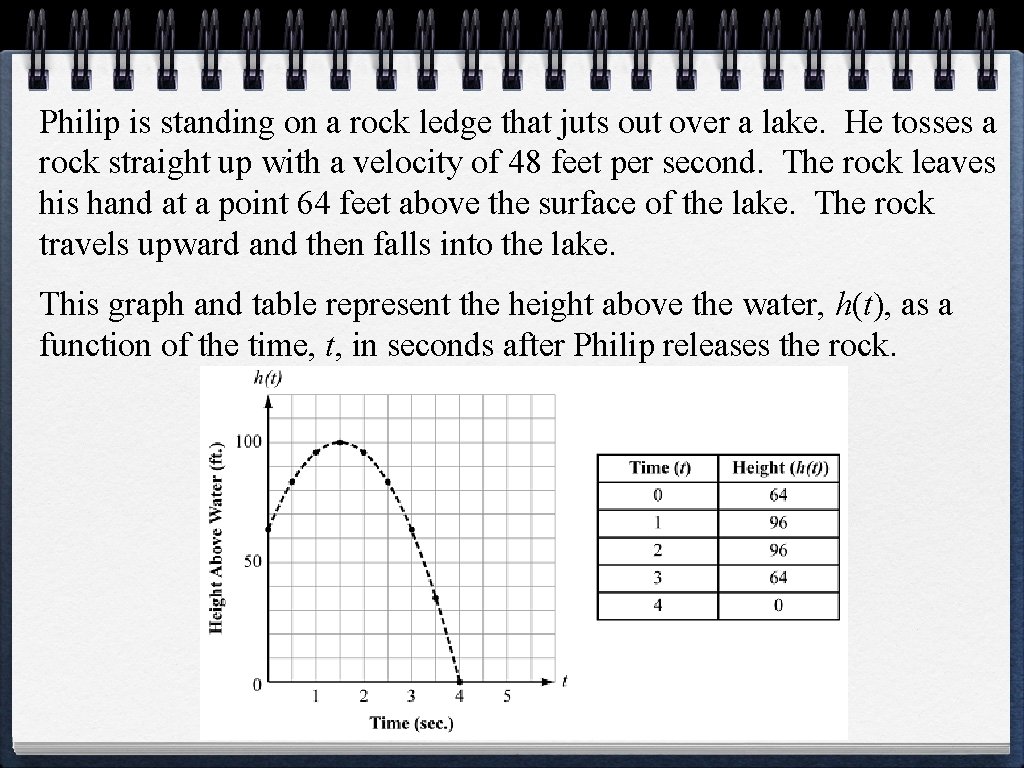
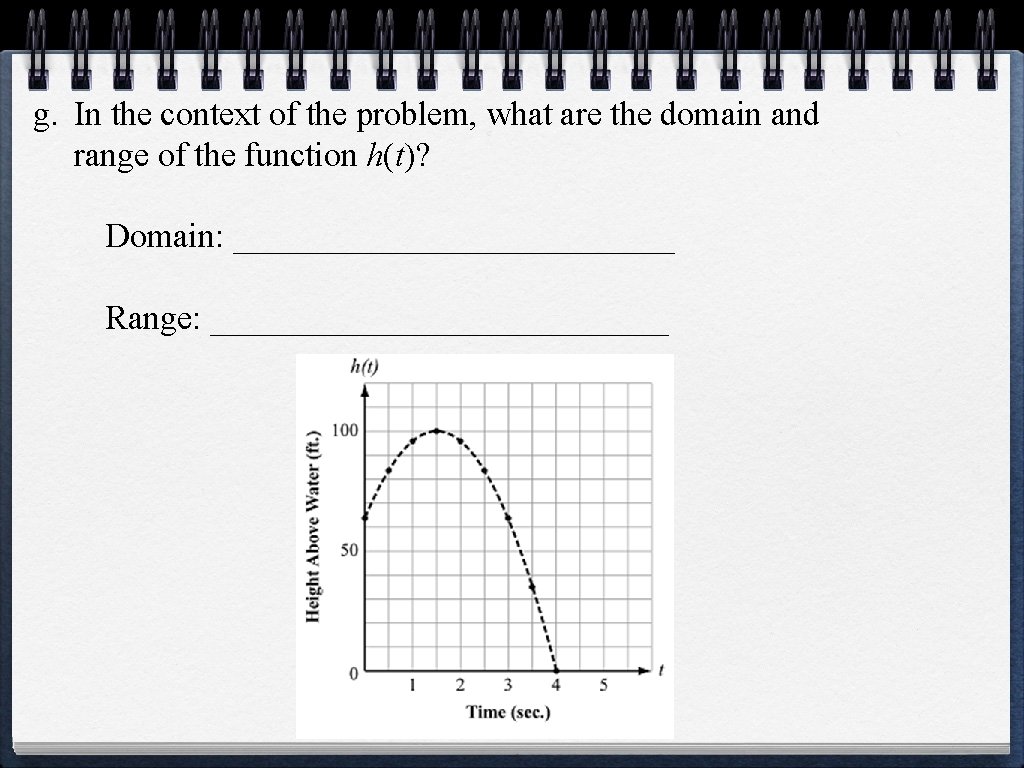
Philip is standing on a rock ledge that juts out over a lake. He tosses a rock straight up with a velocity of 48 feet per second. The rock leaves his hand at a point 64 feet above the surface of the lake. The rock travels upward and then falls into the lake. This graph and table represent the height above the water, h(t), as a function of the time, t, in seconds after Philip releases the rock.

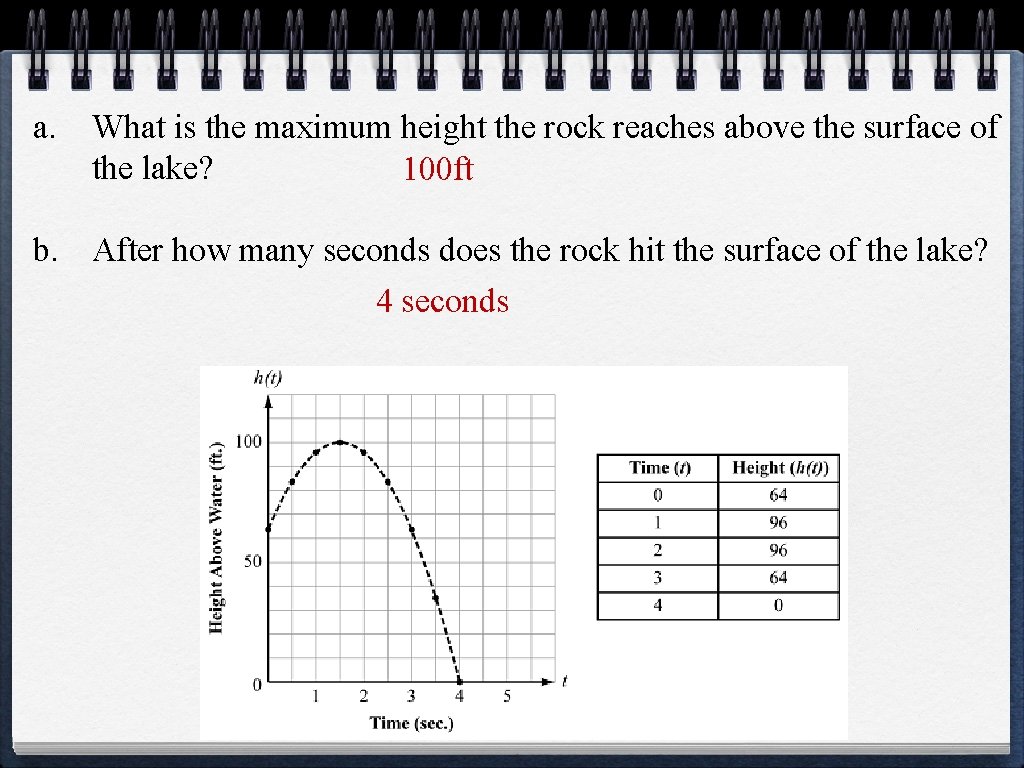
a. What is the maximum height the rock reaches above the surface of the lake? 100 ft b. After how many seconds does the rock hit the surface of the lake? 4 seconds

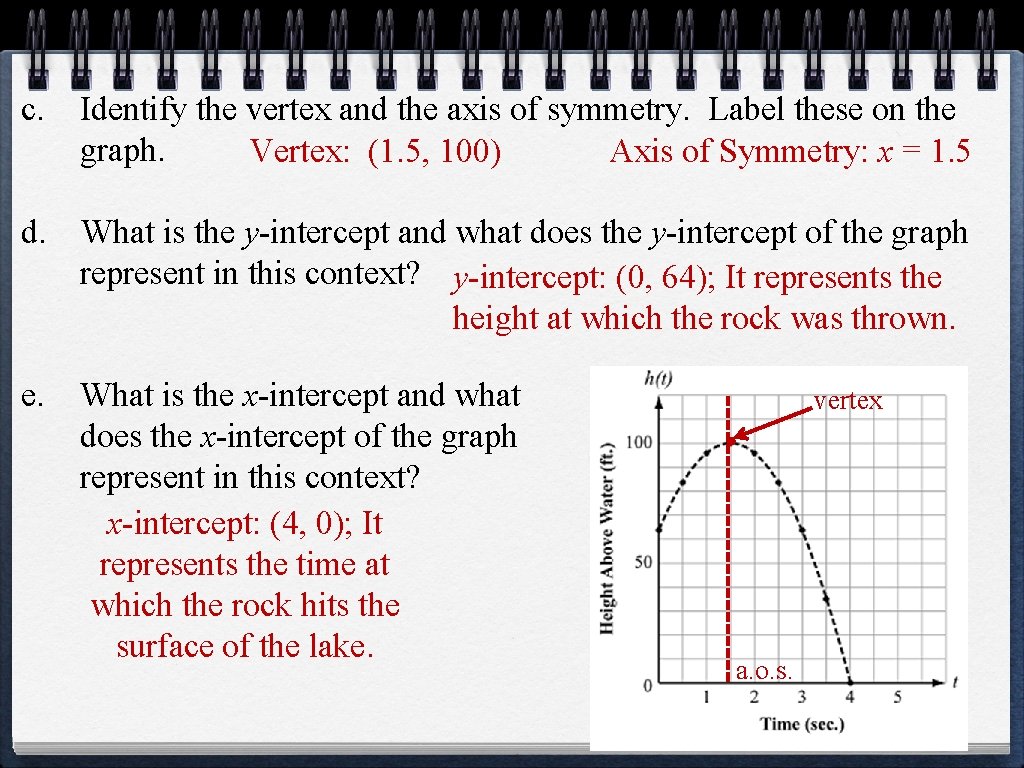
c. Identify the vertex and the axis of symmetry. Label these on the graph. Vertex: (1. 5, 100) Axis of Symmetry: x = 1. 5 d. What is the y-intercept and what does the y-intercept of the graph represent in this context? y-intercept: (0, 64); It represents the height at which the rock was thrown. e. What is the x-intercept and what does the x-intercept of the graph represent in this context? x-intercept: (4, 0); It represents the time at which the rock hits the surface of the lake. vertex a. o. s.

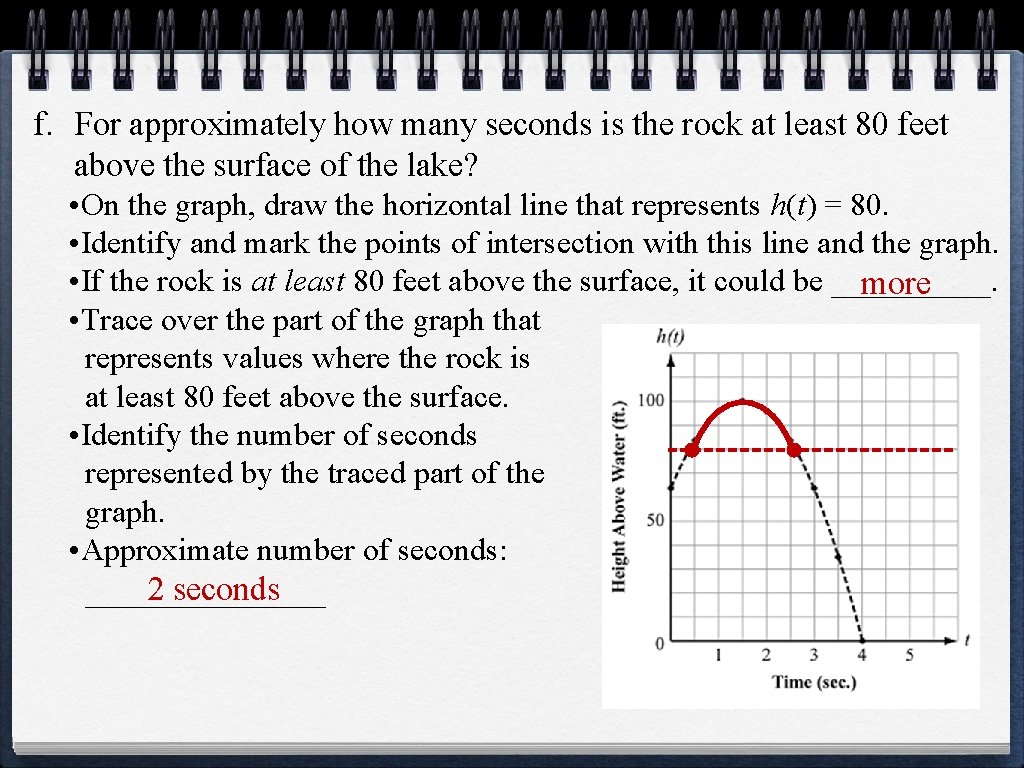
f. For approximately how many seconds is the rock at least 80 feet above the surface of the lake? • On the graph, draw the horizontal line that represents h(t) = 80. • Identify and mark the points of intersection with this line and the graph. • If the rock is at least 80 feet above the surface, it could be _____. more • Trace over the part of the graph that represents values where the rock is at least 80 feet above the surface. • Identify the number of seconds represented by the traced part of the graph. • Approximate number of seconds: 2 seconds _ _______

g. In the context of the problem, what are the domain and range of the function h(t)? Domain: _____________ Range: ______________

h. Write a function in the form that is represented by the graph. • Substitute the vertex (h, k) that you found in part ‘c’ and a point (t, h(t)) from the table into the equation. My point (t, h(t)) is: (4, 0) _______ • Solve for a. • Now that you know a, h, and k, substitute these values into the formula to write the function in vertex form.

i. Write the function from part ‘h’ in standard form: j. Explain, in context, how the values a, b, and c in your function from part ‘i’ relate to the original situation. • a represents the force of gravity (negative means it’s in the downward direction) • b represents the initial velocity (positive means it’s in the upward direction) • c represents the initial height of the rock when it was released