Quadratic Interpolation If 3 data points are available

Quadratic Interpolation If 3 data points are available, a 2 nd-order poly can sed to approximate the curve. 2 -order F 2(x)=bo +b 1(x-xo)+b 2(x-xo) (x-x 1) nd 1 st -order Is equivalent to F 2(X)=ao+a 1 x+a 2 x^2 xx 2 o 1 x 1 Unique polynomial join the 3 points

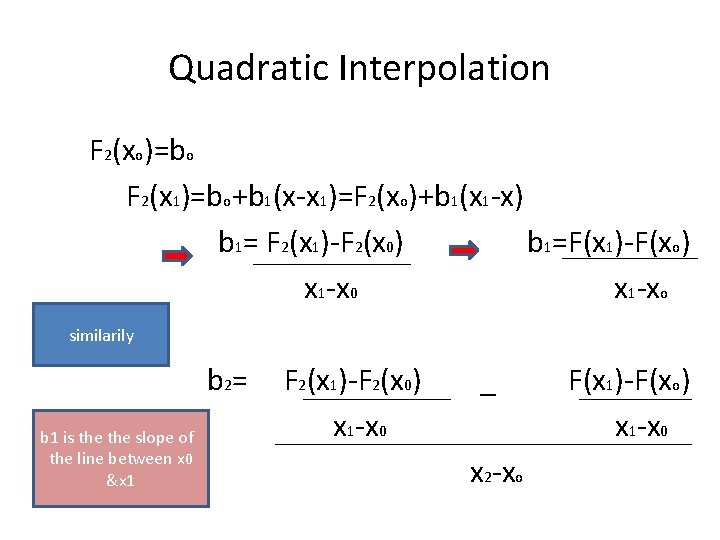
Quadratic Interpolation F 2(xo)=bo F 2(x 1)=bo+b 1(x-x 1)=F 2(xo)+b 1(x 1 -x) b 1= F 2(x 1)-F 2(x 0) b 1=F(x 1)-F(xo) x 1 -x 0 x 1 -xo similarily b 2= b 1 is the slope of the line between x 0 &x 1 F 2(x 1)-F 2(x 0) x 1 -x 0 _ x 2 -xo F(x 1)-F(xo) x 1 -x 0

Example 2 nd –order polynomial to the following point : x 0=1 , F(x 0)=0 x 1=4 , F(x 1)=1. 386 x 2=6 , F(x 2)=1. 791 Then use the resulting polynomial to evaluate ln 2

solution F 2(x)=b 0+b 1(x-x 0)+b 2(x-x 0)(x-x 1) The 2 nd –order finite divided difference is : F[xi, xj, xk]=(F[xi, xj]-F[xj, xk])/(xi-xk). Newton’s divided-difference interpolating polynomial � FFU(x)=F(x 0)+(x-x 0)F[x 1, x 0]+(x-x 0)(x-x 1) F[x 2, x 1, x 0]+…. . +(xx 0)(x-x 1). . (x-xn-1)F[xn, xn-1, …x 0]

Example Estimate ln(2) with a 3 rd -order newton’s interpolating polynomial using the following data points: X 0 1 F(x 0) 0 X 1 4 F(x 1) 1. 386 X 2 6 F(x 2) 1. 792 X 3 5 F(x 3) 1. 609

solution The 3 rd –order polynomial is: F 3(x)=b 0+b 1(x-x 0)+b 2(x-x 0) (x-x 1)+b 3(x-xo) (x-x ) (x- ences: F[x 1, xo]=(1. 386 -0)/(4 -1)=0. 462=b 1 F[x 2, x 1]=(1. 792 -1. 386)/(6 -4)=0. 203 F[x 3, x 2]=(1. 609 -1. 792)/(5 -6)=0. 182 2 nd Divided differences: F[x 2, x 1, x 0]=(0. 203 -0. 462)/(6 -1)=-0. 0519 F[x 3, x 2, x 1]=(0. 182 -0. 205)/(5 -4)=-0. 0204 1 x) 2

Solution 3 rd Divided difference: F[x 3, x 2, x 1, x 0]=(-0. 0204 -(-0. 0519))/(5 -1)=0. 00787=b 3 F 3(x)=0+0. 462(x-1)-0. 0519(x-1)(x-4)+0. 00787(x-1)(x 4)(x-6) F 3(2)=0. 6288 Ɛt=9. 3% The End

Error of Newton’s Interpolation polynomials The general form of the interpolating polynomial (F(X))is similar to the taylor series expansion in that the sense terms are added sequentially to capture the giger-order behavior of the function. The truncation error for taylor series is: Ru=((F^(n+1)(ƺ))/(n+1)!)*(xi+1 -xi)^(n+1) The error for an nth-order interpolating polynomial: Ru=((F^(n+1)(ƺ))/(n+1)!)*(x-x 0) (x-x 1)(x-x 2)………. (x-xn) Xi<ƺ<xi+1

Error of Newton’s Interpolation polynomials The function should be Known and differentiable since the function is usually not Known the derivative is approximation by afinitedivided difference then Ru becomes: Ru=F[x, xn-1, ……. x 0](x-x 0)(x-x 1)…(x-xn) Finite devided diference But F(x) is un known , ther for Ru becoms : Ru~=F[xn+1, xn-1, …, x 0](x-x 0)(x-x 1). . (x-xn) Provided F(xn+1)is known. Data point