Quadratic Graphs Parabolas 1 To draw a quadratic

Quadratic Graphs - Parabolas 1. To draw a quadratic graph from y = ax 2 + bx + c 2. Make up a table of values 3. Draw a smooth curve through the points plotted 4. The shape created is called a parabola

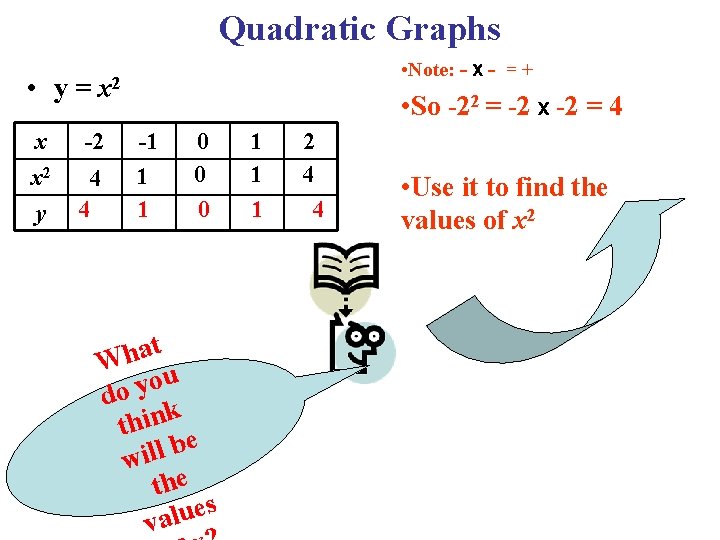
Quadratic Graphs • Note: - X - = + • y = x 2 x x 2 y -2 4 4 • So -22 = -2 X -2 = 4 -1 1 1 0 0 0 t a h W u o y do k thin e b l l i w the s e u l va 1 1 1 2 4 4 • Use it to find the values of x 2

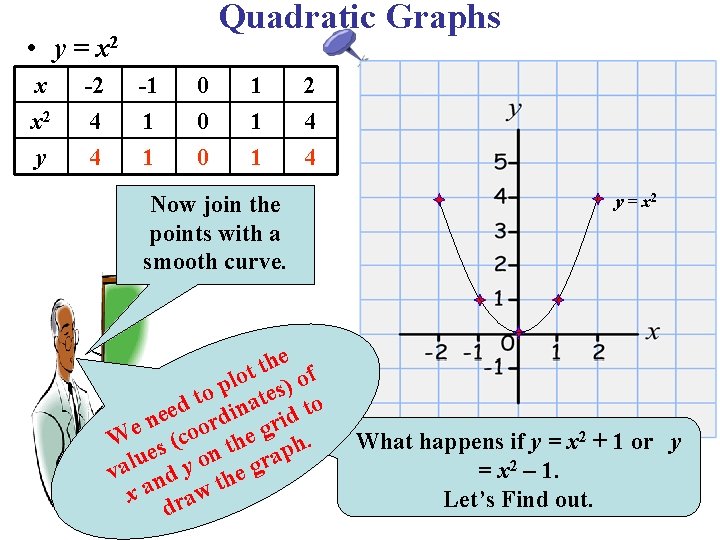
Quadratic Graphs • y = x 2 x x 2 y -2 4 4 -1 1 1 0 0 0 1 1 1 2 4 4 Now join the points with a smooth curve. e h t lot s) of p to nate to d ee rdi rid n We s (coo the g h. p e n a u o r l va nd y the g x a raw d y = x 2 What happens if y = x 2 + 1 or y = x 2 – 1. Let’s Find out.

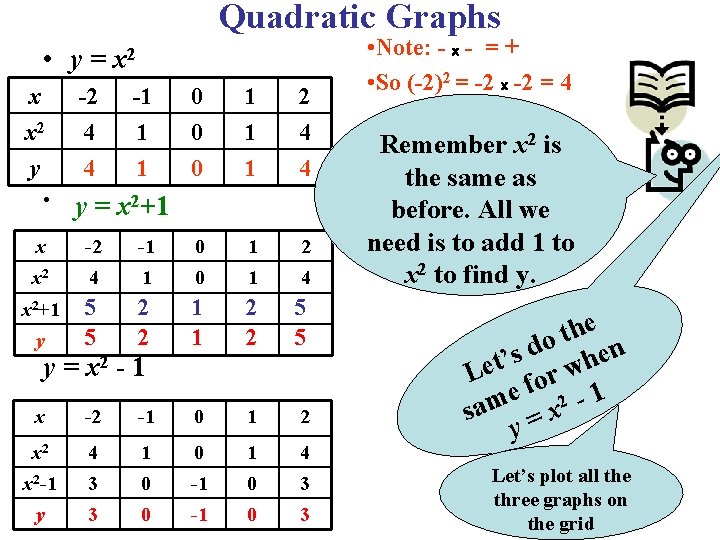
Quadratic Graphs • y= x x 2 y • -2 4 4 x 2 -1 1 1 0 0 0 1 1 1 2 4 4 y = x 2+1 x -2 -1 0 1 2 x 2 4 1 0 1 4 x 2+1 5 5 2 2 1 1 2 2 5 5 y y = x 2 - 1 x -2 -1 0 1 2 x 2 4 1 0 1 4 x 2 -1 3 0 -1 0 3 y 3 0 -1 0 3 • Note: - x - = + • So (-2)2 = -2 x -2 = 4 Remember x 2 is the same as before. All we need is to add 1 to x 2 to find y. e h t o d n e s ’ h t Le for w e 2 -1 m sa = x y Let’s plot all the three graphs on the grid

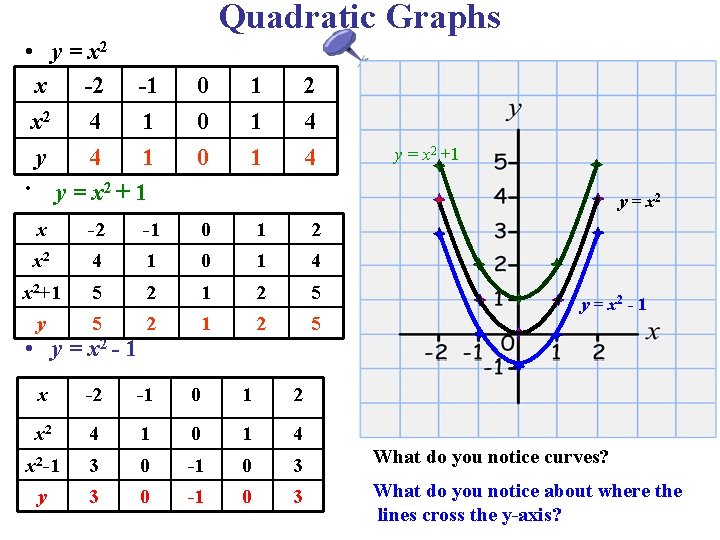
Quadratic Graphs • y = x 2 x -2 -1 x 2 4 1 y 4 1 • y = x 2 + 1 0 0 0 1 1 1 2 4 4 y = x 2 +1 y = x 2 x -2 -1 0 1 2 x 2 4 1 0 1 4 x 2+1 5 2 1 2 5 y 5 2 1 2 5 x -2 -1 0 1 2 x 2 4 1 0 1 4 x 2 -1 3 0 -1 0 3 What do you notice curves? y 3 0 -1 0 3 What do you notice about where the lines cross the y-axis? • y = x 2 - 1

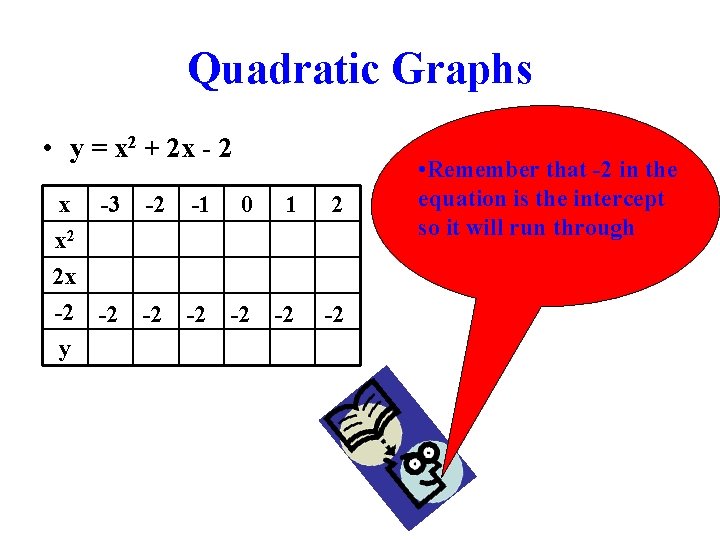
Quadratic Graphs • y = x 2 + 2 x - 2 x -3 -2 -1 0 1 x 2 2 x -2 -2 -2 y 2 -2 • Remember that -2 in the equation is the intercept so it will run through

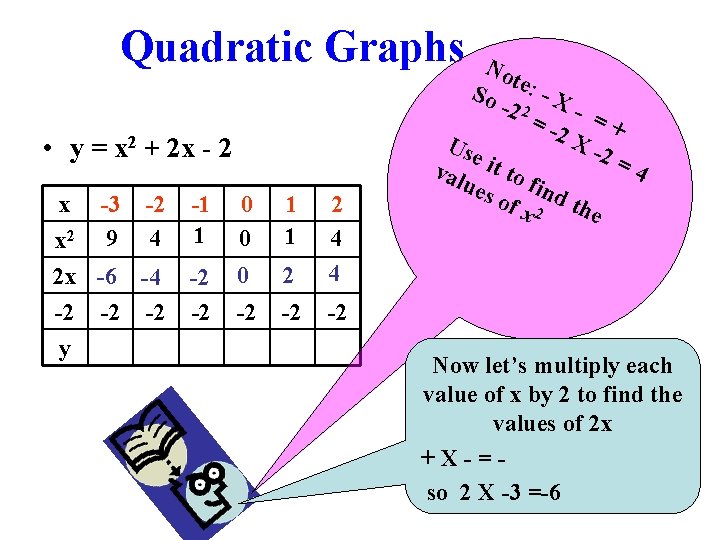
Quadratic Graphs • y = x 2 + 2 x - 2 x -3 -2 x 2 9 4 2 x -6 -4 -2 -2 -2 y -1 1 0 0 1 1 -2 -2 0 2 2 4 4 -2 -2 -2 No t So e: - X -2 2 =- - =+ 2 X Use -2 = i val t to 4 ues fin of x 2 d th e Now let’s multiply each value of x by 2 to find the values of 2 x +X-=so 2 X -3 =-6

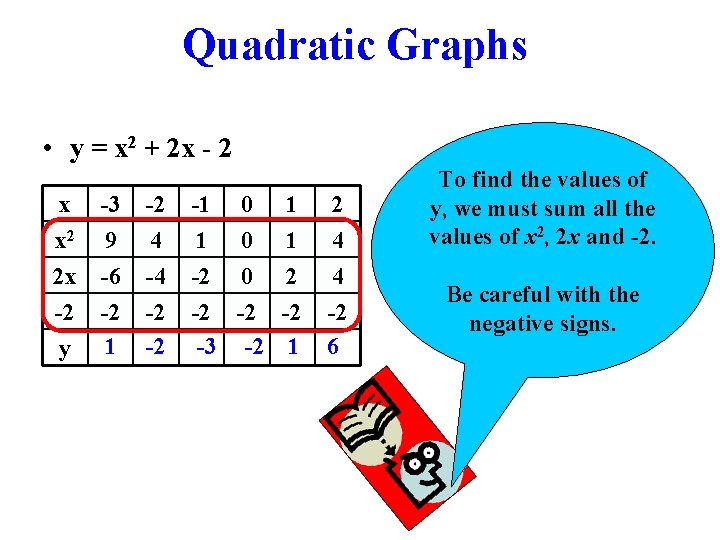
Quadratic Graphs • y = x 2 + 2 x - 2 x -3 x 2 9 2 x -6 -2 -2 y 1 -2 4 -4 -2 -2 -1 1 -2 -2 -3 0 0 0 -2 -2 1 1 2 -2 1 2 4 4 -2 6 To find the values of y, we must sum all the values of x 2, 2 x and -2. Be careful with the negative signs.

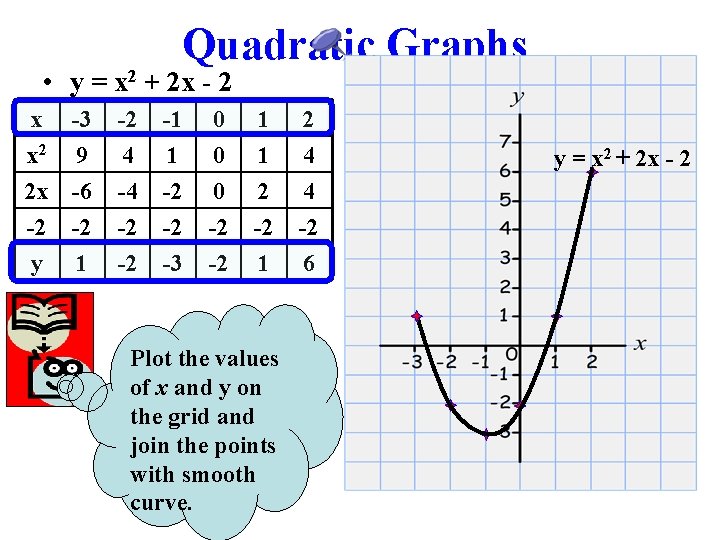
Quadratic Graphs • y = x 2 + 2 x - 2 x -3 x 2 9 2 x -6 -2 -2 -2 4 -4 -2 -1 1 -2 -2 0 0 0 -2 1 1 2 -2 2 4 4 -2 y -2 -3 -2 1 6 1 Plot the values of x and y on the grid and join the points with smooth curve. y = x 2 + 2 x - 2

Quadratic Graphs • y = x 2 – 3 x - 2 x -1 x 2 1 -3 x -2 -2 More negative values 0 1 2 3 4 0 1 4 9 16 -2 -2 -2 • Remember that -2 in the equation is the intercept so it will run through y Note: - X - = + So -12 = -1 X -1 = 1 2. These x f o s e lu a v e Use it to find th mbers. u n e r a u sq y r a in d r o e are just th

Quadratic Graphs • y = x 2 – 3 x - 2 x x 2 -3 x -2 y -1 1 3 -2 2 0 0 0 1 1 -3 2 4 -6 -2 -2 -2 -4 More negative values 3 4 9 16 -9 -12 -2 -2 -2 2 • Multiply each value of x by -3. -X-=+ -X+=- m su st u m e w , y f o s e lu a v To find the -2. d n a x 2 , 2 x f o s e lu a v e all th ve signs. Be careful with negati.

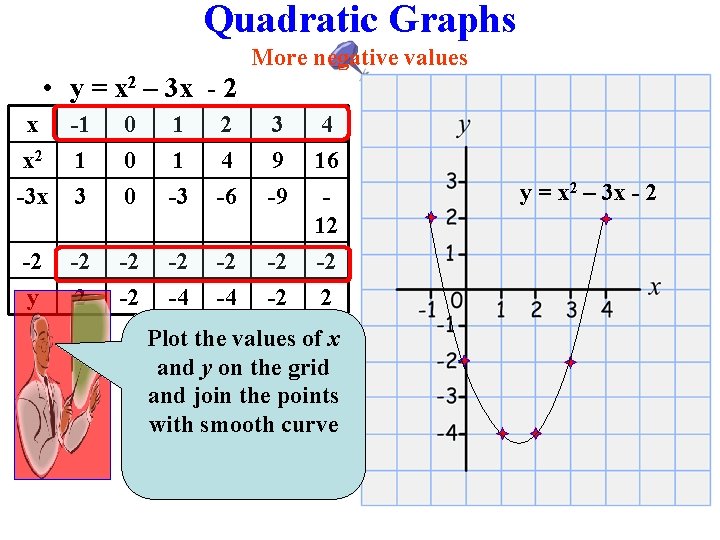
Quadratic Graphs More negative values • y = x 2 – 3 x - 2 x -1 x 2 1 -3 x 3 0 0 0 1 1 -3 2 4 -6 3 9 -9 4 16 12 -2 y -2 -2 -2 -4 -2 -2 -2 2 Plot the values of x and y on the grid and join the points with smooth curve y = x 2 – 3 x - 2

y = x 2 + 2 x -15 x -6 -5 -4 y 7 0 -7 -3 -12 -2 -15 -1 -16 0 -15 1 -12 2 3 4 -7 0 7

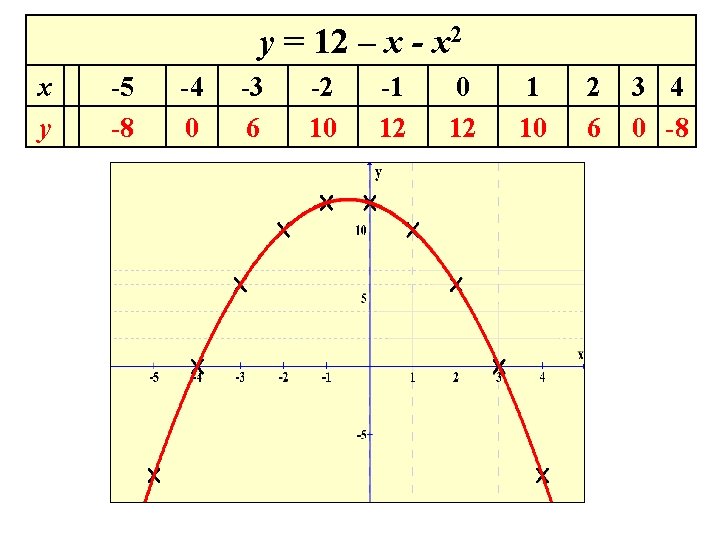
y = 12 – x - x 2 x y -5 -8 -4 0 -3 6 -2 10 -1 12 0 12 1 10 2 6 3 4 0 -8

Quadratic Equations All quadratic expressions involve x 2: y = ax 2 + bx + c The graphs of Quadratics are always parabolas x 2 positive x 2 negative The points at which these graphs cut the x-axis are called the solution or roots of the equation

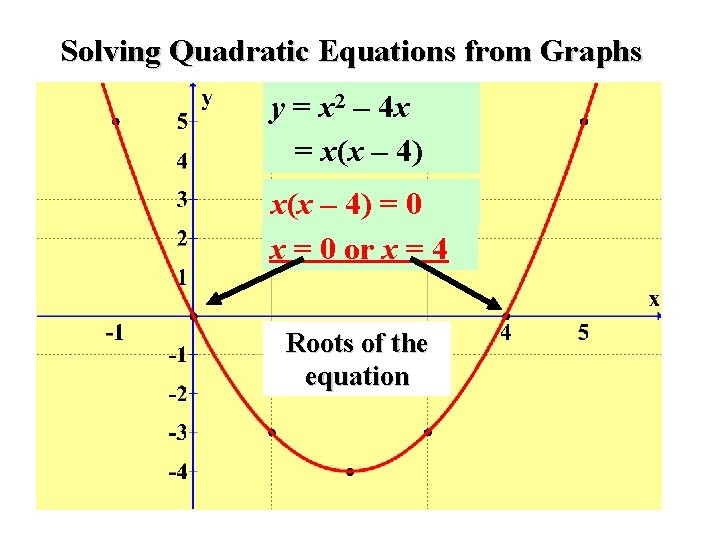
Solving Quadratic Equations from Graphs y = x 2 – 4 x = x(x – 4) = 0 x = 0 or x = 4 Roots of the equation

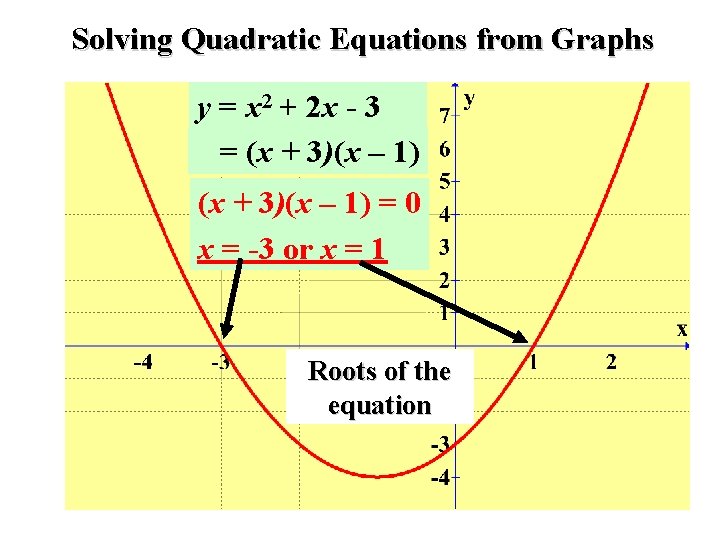
Solving Quadratic Equations from Graphs y = x 2 + 2 x - 3 = (x + 3)(x – 1) = 0 x = -3 or x = 1 Roots of the equation

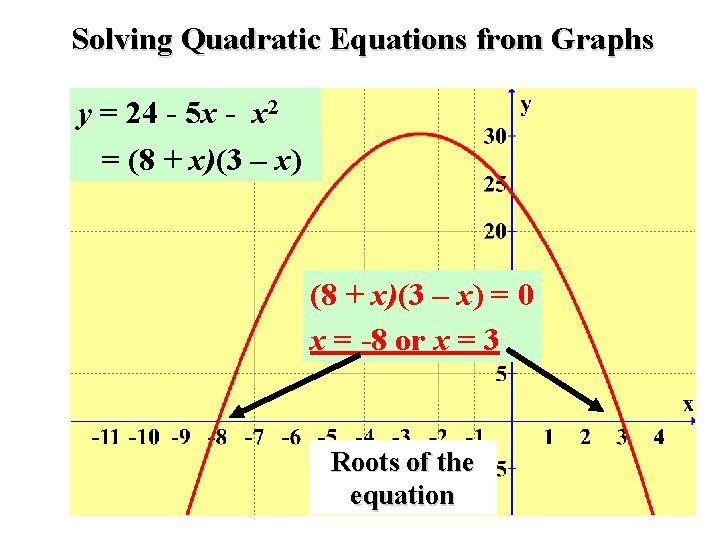
Solving Quadratic Equations from Graphs y = 24 - 5 x - x 2 = (8 + x)(3 – x) = 0 x = -8 or x = 3 Roots of the equation

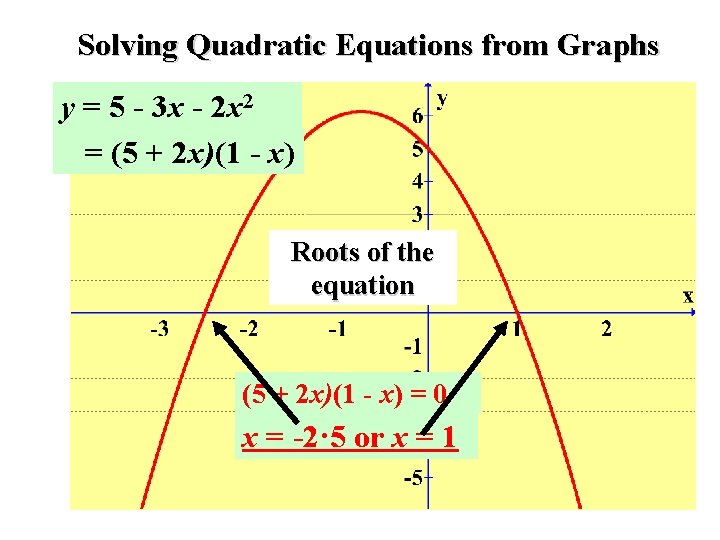
Solving Quadratic Equations from Graphs y = 5 - 3 x - 2 x 2 = (5 + 2 x)(1 - x) Roots of the equation (5 + 2 x)(1 - x) = 0 x = -2· 5 or x = 1

Factorise and Solve ( find the roots of) Mixture of examples

Roots When a number is multiplied by 0 the result is 0. If 7 b = 0 then b = 0 If ab = 0 then a = 0 or b = 0 If (x - a)(x - b) = 0 then either (x - a) = 0 or (x - b) = 0 x = a or x=b 3 x(x + 4) = 0 3 x = 0 or x + 4 = 0 x = 0 or x = -4 (x – 7)(x + 4) = 0 x – 7 = 0 or x + 4 = 0 x = 7 or x = -4

Mixture of examples Set 1 1. 3 x 2 – 7 x = 0 x(3 x – 7) = 0 2. 4 x 2 – 9 = 0 (2 x + 3)(2 x – 3) = 0 x = 0 or 3 x – 7 = 0 2 x + 3 = 0 or 2 x – 3 = 0 x = 0 or x = 7/3 x = - 3/2 or x = 3/2 3. x 2 - 7 x + 10 = 0 (x - 2)(x – 5) = 0 4. x 2 - 2 x - 48 = 0 (x - 8)(x + 6) = 0 x – 2 = 0 or x – 5 = 0 x – 8 = 0 or x + 6 = 0 x = 2 or x = 5 x = 8 or x = -6

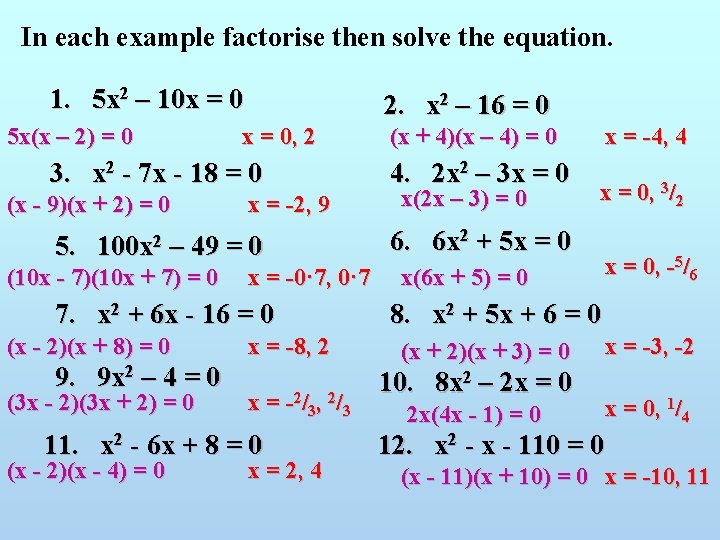
In each example factorise then solve the equation. 1. 5 x 2 – 10 x = 0 5 x(x – 2) = 0 2. x 2 – 16 = 0 x = 0, 2 3. x 2 - 7 x - 18 = 0 (x - 9)(x + 2) = 0 x = -2, 9 5. 100 x 2 – 49 = 0 (10 x - 7)(10 x + 7) = 0 x = -0· 7, 0· 7 7. x 2 + 6 x - 16 = 0 (x - 2)(x + 8) = 0 9. 9 x 2 – 4 = 0 (3 x - 2)(3 x + 2) = 0 x = -8, 2 x = -2/3, 2/3 11. x 2 - 6 x + 8 = 0 (x - 2)(x - 4) = 0 x = 2, 4 (x + 4)(x – 4) = 0 4. 2 x 2 – 3 x = 0 x(2 x – 3) = 0 x = -4, 4 x = 0, 3/2 6. 6 x 2 + 5 x = 0 x(6 x + 5) = 0 x = 0, -5/6 8. x 2 + 5 x + 6 = 0 (x + 2)(x + 3) = 0 10. 8 x 2 – 2 x = 0 2 x(4 x - 1) = 0 x = -3, -2 x = 0, 1/4 12. x 2 - x - 110 = 0 (x - 11)(x + 10) = 0 x = -10, 11

When we cannot factorise or solve quadratic equations graphically we need to use the quadratic formula. If ax 2 + bx + c = 0 then

Example : Solve x 2 + 3 x – 3 = 0 ax 2 + bx + c = 0 1 3 = 0· 79 or – 3· 8 -3

Example 2 Use the quadratic formula to solve the equation : x 2 + 5 x + 6= 0 ax 2 + bx + c= 0 1 5 6 x = - 2 or x = - 3 These are the roots of the equation.

Example 3 Use the quadratic formula to solve the equation : 8 x 2 + 2 x - 3= 0 ax 2 + bx + c= 0 8 2 -3 x = 1/2 or x = - 3/4 These are the roots of the equation.

Example 4 Use the quadratic formula to solve the equation : 8 x 2 - 22 x + 15 = 0 ax 2 + bx + c= 0 8 -22 15 x = 3/2 or x = 5/4 These are the roots of the equation.

Example 5 Use the quadratic formula to solve the equation : 2 x 2 + 3 x - 7 = 0 ax 2 + bx + c= 0 2 3 -7 x = 1· 27 or x = -2· 77 These are the roots of the equation.

Use quadratic formula to solve the following : 2 x 2 + 4 x + 1 = 0 x 2 + 3 x – 2 = 0 x = -1· 7, -0· 3 x = -3· 6, 0· 6 5 x 2 - 9 x + 3 = 0 3 x 2 - 3 x – 5 = 0 x = 1· 4, 0· 4 x = 1· 9, -0· 9 4 x 2 - x - 1 = 0 x 2 + 2 x - 5 = 0 x = -0· 39, 0· 64 x = 1· 45, -3· 45

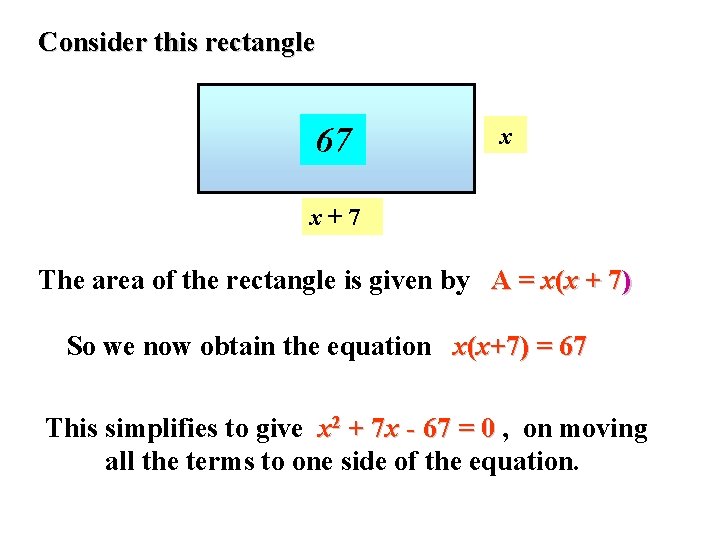
Consider this rectangle 67 x x+7 The area of the rectangle is given by A = x(x + 7) So we now obtain the equation x(x+7) = 67 This simplifies to give x 2 + 7 x - 67 = 0 , on moving all the terms to one side of the equation.

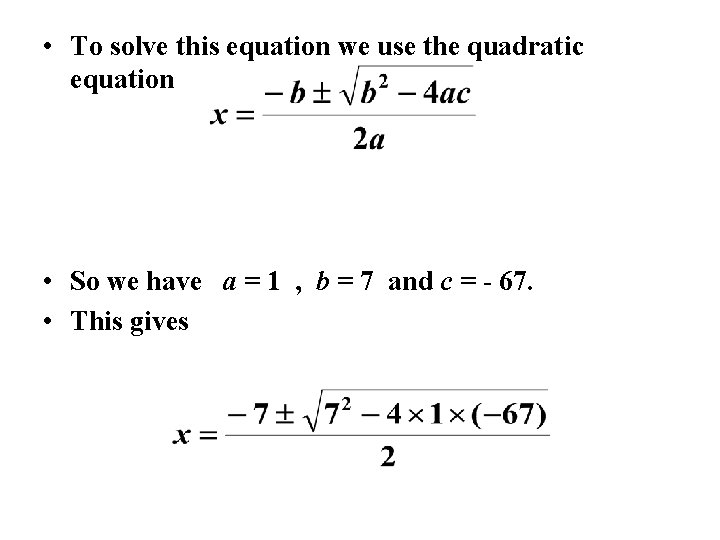
• To solve this equation we use the quadratic equation • So we have a = 1 , b = 7 and c = - 67. • This gives

• This simplifies to • Which leads to • So • Giving the two solutions x = 5· 40 and -12· 40

• Now x ≠ -12. 40 as you cannot have a negative length of side so we are left with the solution that x = 5· 40

• Find x in each of the examples below. 93 x+8 37 x+4 x+2

Quadratic formula mixed examples The roots of ax 2 + bx + c = 0 are 1. Solve x 2 - x – 5 = 0 , giving the roots correct to 1 decimal place. 2. Solve 2 x 2 – 5 x + 1, giving the roots correct to 2 decimal places. 3. Solve 2 x(x - 1) = 7 giving the roots correct to 1 decimal place. 4. The area of the rectangle shown is 43 sq. cm. Find x correct to 1 decimal place. x+1 x+5

5. Use Pythagoras to form an equation in x and then solve it. The triangle is right angled. x x+5 x+3 6. A quadratic equation shown has equation y = x 2 – 8 x + 11. Find the coordinates of the points where the curve cuts the x axis. 7. The height h of the object above the ground after a time t seconds is given by h = 15 t – t 2 When is the object 9 metres above the ground ? Explain the meaning of the two answers.

Quadratics Cutting the x and y axis. In each of the example: a) Find the points where the quadratic cuts the x and the y axis; b) Use symmetry to determine the coordinates of the turning point.

Ex 1. Sketch the graph of y = x 2 + 5 x - 24 Will the graph be “happy” or “sad” x 2 positive, so “happy” Solve x 2 + 5 x – 24 = 0 The graph cuts the x-axis when y = 0 Now factorise (x + 8)(x – 3) = 0 Solving gives x + 8 = 0 or x – 3 = 0 x = -8 or x = 3 Graph cuts y-axis at x = 0 y = 02 +5(0) - 24 Graph cuts the x-axis at (-8, 0) and (3, 0) Cuts y axis at (0, -24) By symmetry the x co-ordinate of turning point is midpoint of the roots -8 and 3. x = (-8 + 3) ÷ 2 = -2· 5 When x = 2· 5, y = 2· 52 + 5(-2· 5) – 24 = 30· 25 Turning point = (-2· 5, -30· 25)

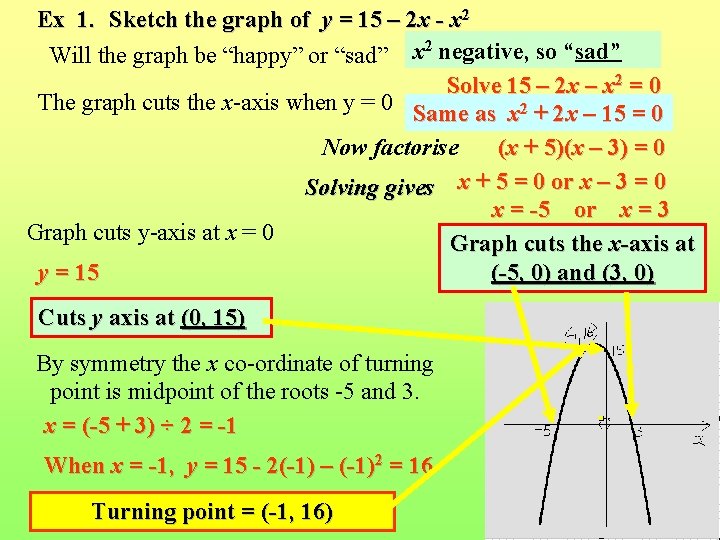
Ex 1. Sketch the graph of y = 15 – 2 x - x 2 Will the graph be “happy” or “sad” x 2 negative, so “sad” Solve 15 – 2 x – x 2 = 0 The graph cuts the x-axis when y = 0 Same as x 2 + 2 x – 15 = 0 Now factorise (x + 5)(x – 3) = 0 Solving gives x + 5 = 0 or x – 3 = 0 x = -5 or x = 3 Graph cuts y-axis at x = 0 Graph cuts the x-axis at y = 15 (-5, 0) and (3, 0) Cuts y axis at (0, 15) By symmetry the x co-ordinate of turning point is midpoint of the roots -5 and 3. x = (-5 + 3) ÷ 2 = -1 When x = -1, y = 15 - 2(-1) – (-1)2 = 16 Turning point = (-1, 16)

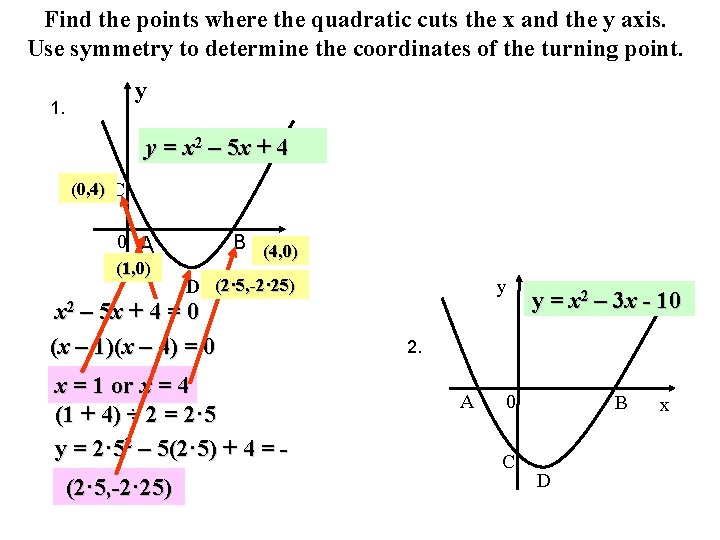
Find the points where the quadratic cuts the x and the y axis. Use symmetry to determine the coordinates of the turning point. y 1. y = x 2 – 5 x + 4 (0, 4) C 0 B (4, 0) x A (1, 0) D (2· 5, -2· 25) – 5 x + 4 = 0 (x – 1)(x – 4) = 0 y x 2 x = 1 or x = 4 (1 + 4) ÷ 2 = 2· 5 y = 2· 52 – 5(2· 5) + 4 = 2(2 · 25 · 5, -2· 25) y = x 2 – 3 x - 10 2. A 0 C B D x

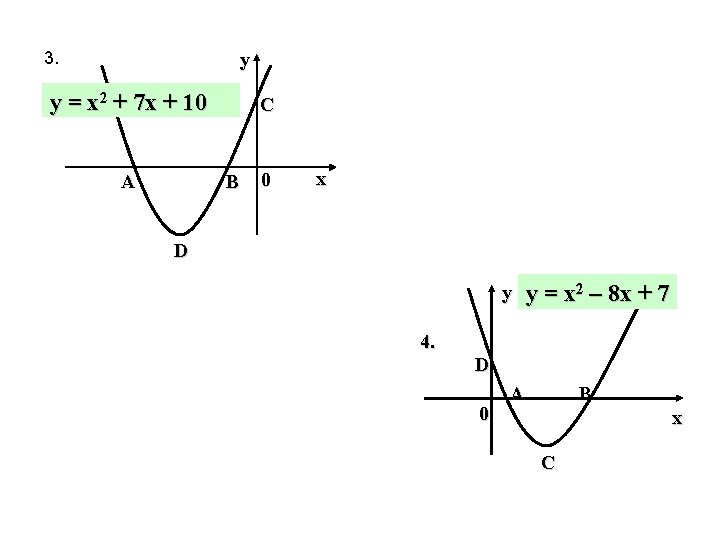
3. y y = x 2 + 7 x + 10 A C B 0 x D y y = x 2 – 8 x + 7 4. D 0 A B x C

y 5. y = x 2 - 9 A 0 B x C y 6. y = x 2 – 6 x 0 A B x

7. y y = x 2 – 4 x - 21 0 A B C x D y 8. y = x 2 – 6 x + 8 C 0 A D B x

y 9. y = x 2 + 7 x - 8 0 B C A x D 10. y y = x 2 + 4 x + 3 C A D B 0 x

Find the points where the quadratic cuts the x and the y axis. Use symmetry to determine the coordinates of the turning point. 1. y C y = 16 – x 2 y A 0 B x C 2. A 0 D y = 4 + 3 x – x 2 B x

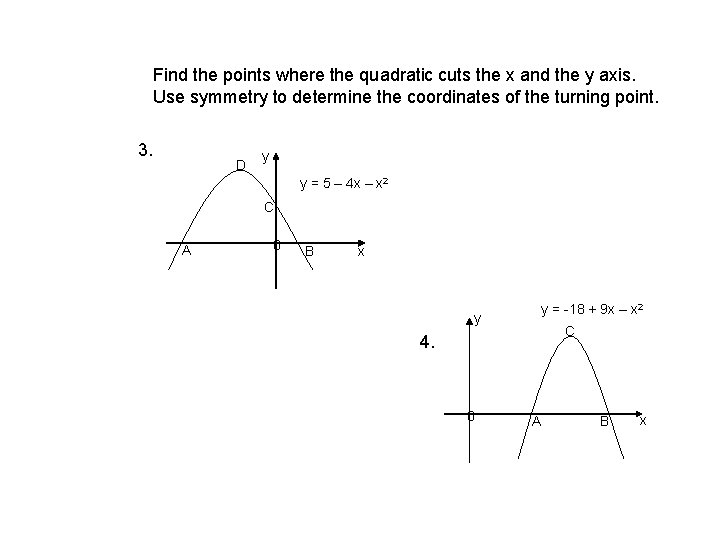
Find the points where the quadratic cuts the x and the y axis. Use symmetry to determine the coordinates of the turning point. 3. D y y = 5 – 4 x – x 2 C A 0 B x y y = -18 + 9 x – x 2 C 4. 0 A B x

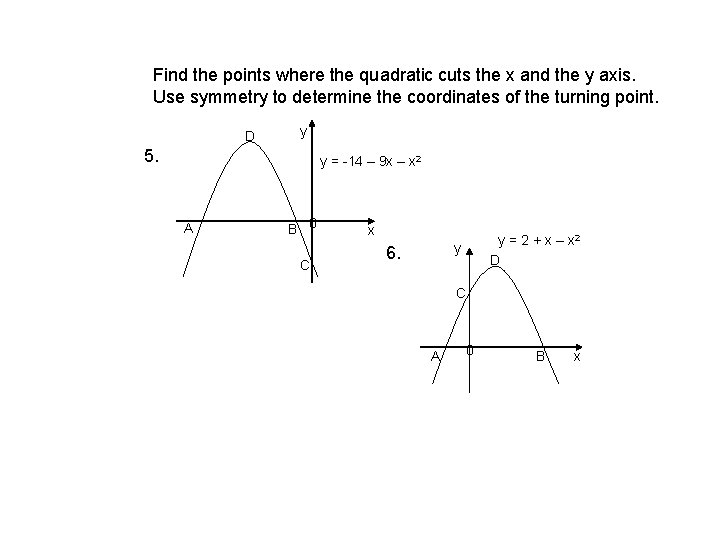
Find the points where the quadratic cuts the x and the y axis. Use symmetry to determine the coordinates of the turning point. D y 5. y = -14 – 9 x – x 2 A B 0 C x y = 2 + x – x 2 D y 6. C A 0 B x

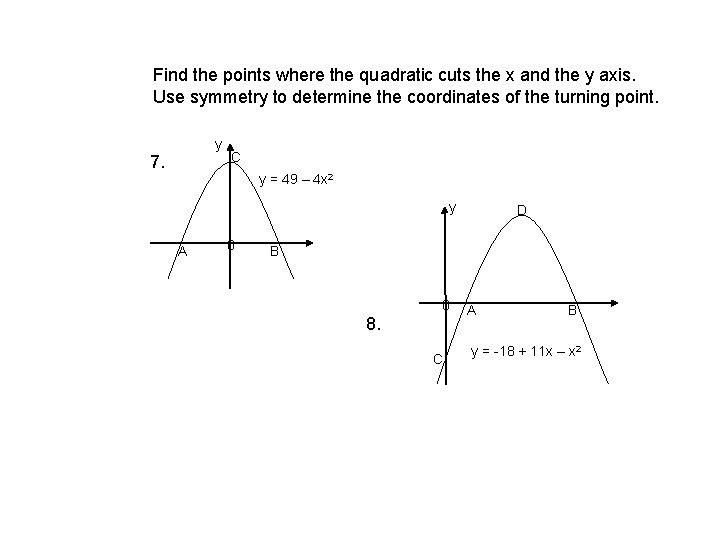
Find the points where the quadratic cuts the x and the y axis. Use symmetry to determine the coordinates of the turning point. y 7. C y = 49 – 4 x 2 y A 0 D B 0 8. C A B y = -18 + 11 x – x 2

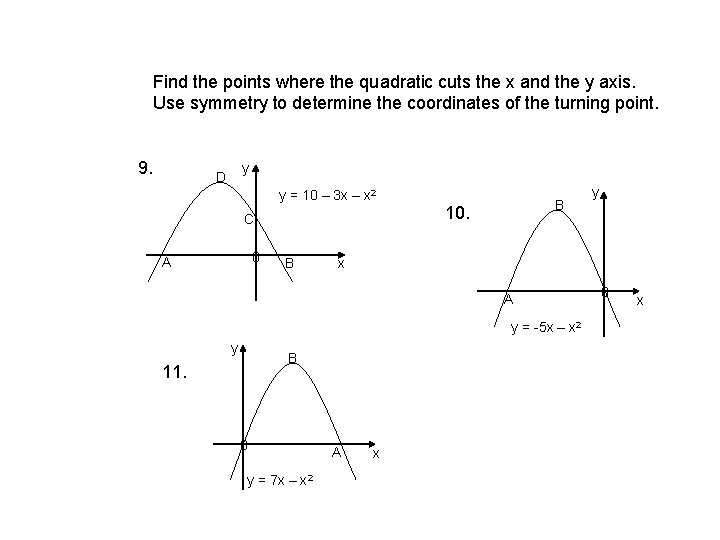
Find the points where the quadratic cuts the x and the y axis. Use symmetry to determine the coordinates of the turning point. 9. y D y = 10 – 3 x – x 2 C 0 A B B 10. x A y = -5 x – x 2 y B 11. 0 y = 7 x – x 2 y A x 0 x