Quadratic Functions Copyright Cengage Learning All rights reserved

Quadratic Functions Copyright © Cengage Learning. All rights reserved. 4

4. 2 Graphing Quadratics in Vertex Form Copyright © Cengage Learning. All rights reserved.

Objectives § Identify the axis of symmetry for a parabola. § Graph a quadratic by hand from the vertex form. § Determine the domain and range for a quadratic function. 3

Vertex Form 4

Vertex Form Understanding the graph of a function is an important part of the modeling process. We are going to take a close look at the vertex form and see how the constants a, h, and k affect the graph of the function. Be cautious when interpreting the value of h and k. Remember that h will appear to have the opposite sign. These two constants control the location of the vertex of the parabola and, therefore, will also give you the values for the maximum or minimum point on the graph. 5

Vertex Form 6

Graphing Quadratics in Vertex Form 7

Graphing Quadratics in Vertex Form The vertex of a parabola can be read directly from the vertex form of the quadratic. f (x) = a(x – h)2 + k vertex = (h, k) The sign of h will look the opposite of what it is. The value of a will affect the width of the graph as well as determine whether the parabola faces upward (positive a) or downward (negative a). 8

Graphing Quadratics in Vertex Form 9

Graphing Quadratics in Vertex Form One other characteristic of a parabola that is helpful is its symmetry about the vertical line going through the vertex. This vertical line is called the axis of symmetry and has the equation x = h, where the vertex is (h, k). Symmetry basically means that the curve on one side of the axis of symmetry is a reflection of the curve on the other side. 10

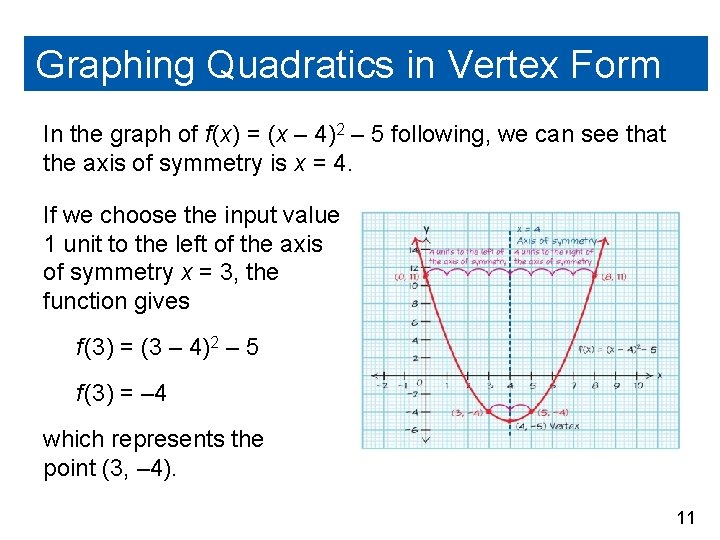
Graphing Quadratics in Vertex Form In the graph of f (x) = (x – 4)2 – 5 following, we can see that the axis of symmetry is x = 4. If we choose the input value 1 unit to the left of the axis of symmetry x = 3, the function gives f (3) = (3 – 4)2 – 5 f (3) = – 4 which represents the point (3, – 4). 11

Graphing Quadratics in Vertex Form If we choose the input value 1 unit to the right of the axis of symmetry x = 5, the function gives f (5) = (5 – 4)2 – 5 f (5) = – 4 which represents the point ( 5, – 4 ). These two points are (equidistant) equally distant from the axis of symmetry and are at the same height. Again if we choose the input values 4 units less than and 4 units greater than the axis of symmetry we get two points that are equidistant from the axis of symmetry with the same height. 12

Graphing Quadratics in Vertex Form Every point on the parabola to the left of the axis of symmetry will have a matching point on the right side of the axis of symmetry. These points are called symmetric points, since they are equidistant from the axis of symmetry and have the same vertical height. 13

Graphing Quadratics in Vertex Form 14

Example 1 – Graphing quadratic functions in vertex form Sketch the graph of the following quadratic function. f (x) = 2. 5(x – 6)2 + 2 Solution: Step 1: Determine whether the graph opens up or down. The value of a is 2. 5. Since a is positive, the graph will open upward, and because it is greater than 1, the graph will be narrow. 15

Example 1 – Solution cont’d Step 2: Find the vertex and the equation for the axis of symmetry. Since the quadratic is given in vertex form, the vertex is (6, 2). The axis of symmetry is the vertical line through the vertex x = 6. Step 3: Find the vertical intercept. To find the vertical intercept, we make the input variable zero. f (x) = 2. 5(x – 6)2 + 2 f (0) = 2. 5(0 – 6)2 +Be 2 sure to follow the order of operations. 16

Example 1 – Solution cont’d f (0) = 2. 5(– 6)2 + 2 f (0) = 2. 5(36) + 2 f (0) = 90 + 2 f (0) = 92 Therefore, the vertical intercept is (0, 92). 17

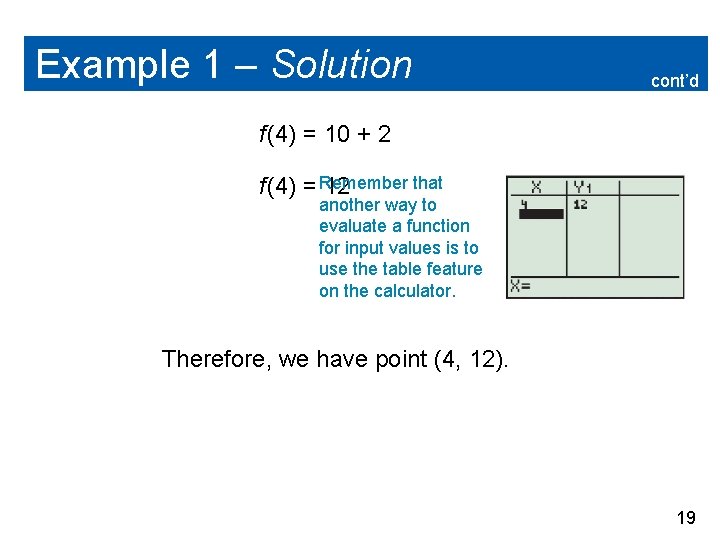
Example 1 – Solution cont’d Step 4: Find an extra point by picking an input value on one side of the axis of symmetry and calculating the output value. The axis of symmetry is x = 6, so we can choose any x-values less than or greater than 6. We will choose x = 4. Substitute 4 into the input of the function to find the output. f (4) = 2. 5(4 – 6)2 + 2 f (4) = 2. 5(– 2)2 + 2 f (4) = 2. 5(4) + 2 18

Example 1 – Solution cont’d f (4) = 10 + 2 that f (4) = Remember 12 another way to evaluate a function for input values is to use the table feature on the calculator. Therefore, we have point (4, 12). 19

Example 1 – Solution cont’d Step 5: Plot the points you found in Step 2 through Step 4. Plot their symmetric points and sketch the graph. (Find an addition pair of symmetric points if needed. ) 20

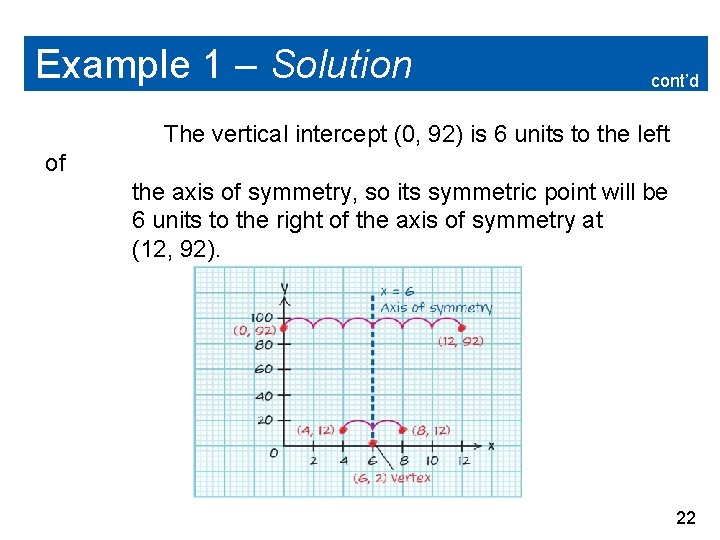
Example 1 – Solution cont’d The vertex is (6, 2), the vertical intercept is (0, 92), and the other point we found in step 4 was (4, 12). The x-values are all small, but the y-values get up to 92 and above, so we will scale the x-axis and y-axis differently. Because (4, 12) is 2 units to the left of the axis of symmetry x = 6, the point 2 units to the right of the axis of symmetry, (8, 12), will be its symmetric point. 21

Example 1 – Solution cont’d The vertical intercept (0, 92) is 6 units to the left of the axis of symmetry, so its symmetric point will be 6 units to the right of the axis of symmetry at (12, 92). 22

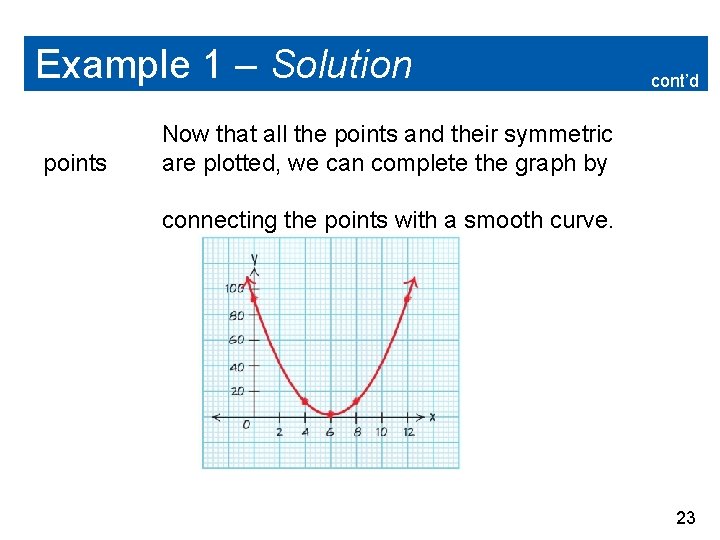
Example 1 – Solution points cont’d Now that all the points and their symmetric are plotted, we can complete the graph by connecting the points with a smooth curve. 23

Domain and Range 24

Domain and Range The domain and range for quadratic models are again restricted to what will make sense in the situation you are modeling. Remember that you might not want to spread out very far in the domain because model breakdown can occur more rapidly with a quadratic model than with a linear one. When you have no data to help guide your domain, you must rely on the situation and any information that will help you to avoid model breakdown. 25

Domain and Range In some cases, only half of the parabola will make sense in the context, so the vertex may be a good starting point or ending point for your domain. 26

Example 5 – Domain and range of quadratic functions with no context Give the domain and range for the following functions. a. f (x) = 2. 5(x – 6)2 + 2 b. f (x) = – 0. 25(x + 8)2 + 10 c. g (x) = (x – 3)2 – 5 27

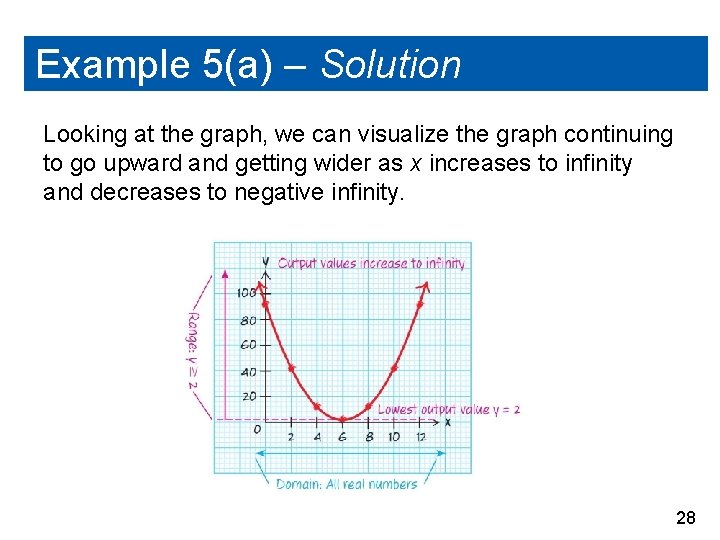
Example 5(a) – Solution Looking at the graph, we can visualize the graph continuing to go upward and getting wider as x increases to infinity and decreases to negative infinity. 28

Example 5(a) – Solution cont’d Because the input variable x can be any real number without causing the function to be undefined, the functions domain is all real numbers. The lowest point on the parabola is the vertex, so the lowest output value for the function is y = 2, and the outputs continue up to infinity. Thus, we get the following: Domain: All real numbers or ( Range: y ≥ 2 or [ 2, ) , ) 29

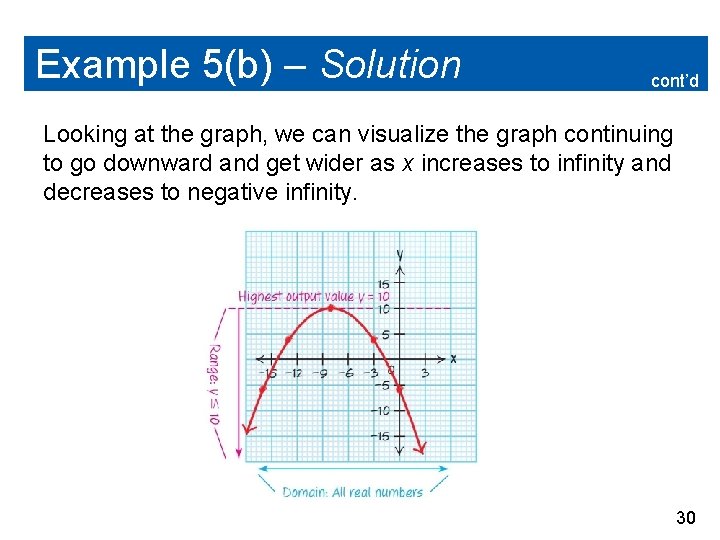
Example 5(b) – Solution cont’d Looking at the graph, we can visualize the graph continuing to go downward and get wider as x increases to infinity and decreases to negative infinity. 30

Example 5(b) – Solution cont’d No real number will make this function undefined, so the domain of the function is all real numbers. The highest point on the parabola is the vertex, so the highest output for the function is y = 10 and goes down to negative infinity from there, so we get the following: Domain: All real numbers or ( Range: y ≤ 10 or ( , 10] , ) 31

Example 5(c) – Solution cont’d Without graphing the function, we know that no real number will make this function undefined, so the domain is all real numbers. Because the function is in vertex form, we know that the vertex is (3, – 5) and that the parabola faces upward, because a is positive. 32

Example 5(c) – Solution cont’d The vertex being the lowest point means that y = – 5 is the lowest output value on the graph. The outputs will continue to go upward to infinity. Thus, we get the following: Domain: All real numbers or ( Range: y ≥ – 5 or [– 5, ) , ) 33