Quadratic Functions and Applications Concepts 1 Graph a

Concepts 1. Graph a Quadratic Function Written in Vertex Form 2. Write f(x) =

Graph a Quadratic Function Written in Vertex Form The graph of the quadratic function

Graph a Quadratic Function Written in Vertex Form The function may be written in

Example 1: Graph the quadratic function. Identify the vertex, x- and y-intercepts, and axis

Example 2: Graph the quadratic function. Identify the vertex, x- and y-intercepts, and axis

Example 3: Use the technique of completing the square to write into vertex form

Example 4: Write in vertex form and graph the function. Identify the vertex, x-

Example 4 continued: Write the domain and range in interval notation.

Write f(x) = ax 2 + bx + c (a ≠ 0) in Vertex

Find the Vertex of a Parabola by Using the Vertex Formula For , the

Example 5: Given determine the vertex by using the vertex formula and by writing

Example 6: At the end of his career, Sherlock Holmes retired to small farm

Example 6 continued: a. What is the maximum height the bee reaches as it

Example 6 continued: b. How far away from Sherlock are flowers A and B?

Example 7: Use regression to find a quadratic function to model the data. Round

Example 7 continued: 1. Use the STAT button, then EDIT to enter the x

Example 7 continued: 2. Use the STAT button, then CALC, choose 5: Quad. Reg.

Example 7 continued: 3. Hit ENTER. Then CALCULATE. The equation is:

Example 7 continued: 4. To see the data and the line graphed: Above the

Example 7 continued: 5. Enter into the equation editor and see the parabola graphed.

Example 7 continued: x 8 f (x) 5 10 12 18 20 23 40

Slides: 34

Download presentation

Quadratic Functions and Applications

Concepts 1. Graph a Quadratic Function Written in Vertex Form 2. Write f(x) = ax 2 + bx + c (a ≠ 0) in Vertex Form 3. Find the Vertex of a Parabola by Using the Vertex Formula 4. Solve Applications Involving Quadratic Functions 5. Create Quadratic Models Using Regression

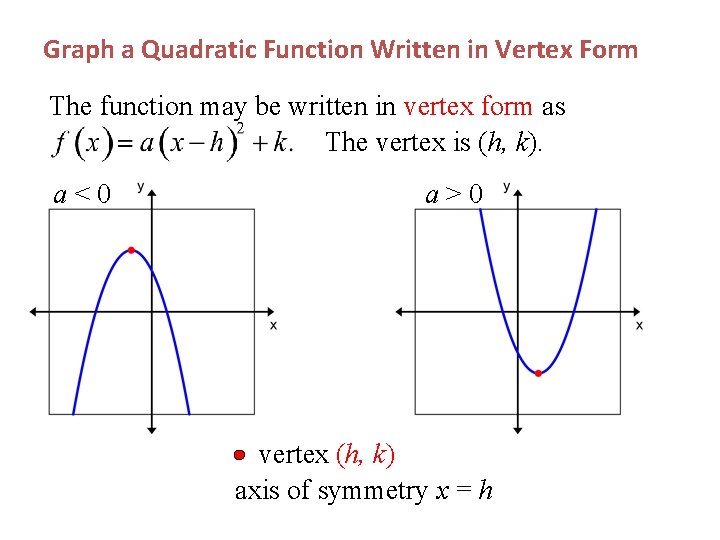
Graph a Quadratic Function Written in Vertex Form The graph of the quadratic function is a parabola. a<0 a>0 The parabola opens upward for a > 0 and opens downward for a < 0

Graph a Quadratic Function Written in Vertex Form The function may be written in vertex form as The vertex is (h, k). a<0 a>0 vertex (h, k) axis of symmetry x = h

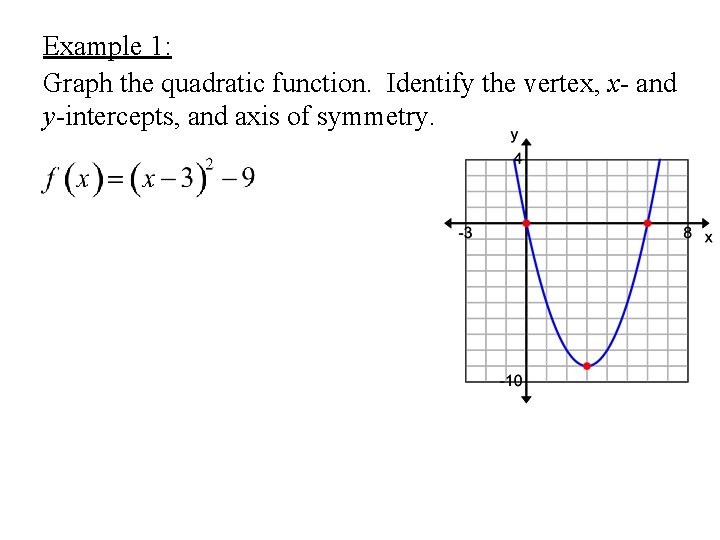
Example 1: Graph the quadratic function. Identify the vertex, x- and y-intercepts, and axis of symmetry.

Example 2: Graph the quadratic function. Identify the vertex, x- and y-intercepts, and axis of symmetry.

Example 3: Use the technique of completing the square to write into vertex form and identify the vertex. Factor out the leading coefficient of the x 2 term from the two terms containing x. Complete the square within parentheses. Remove – 25 from within the parentheses along with a factor of 2.

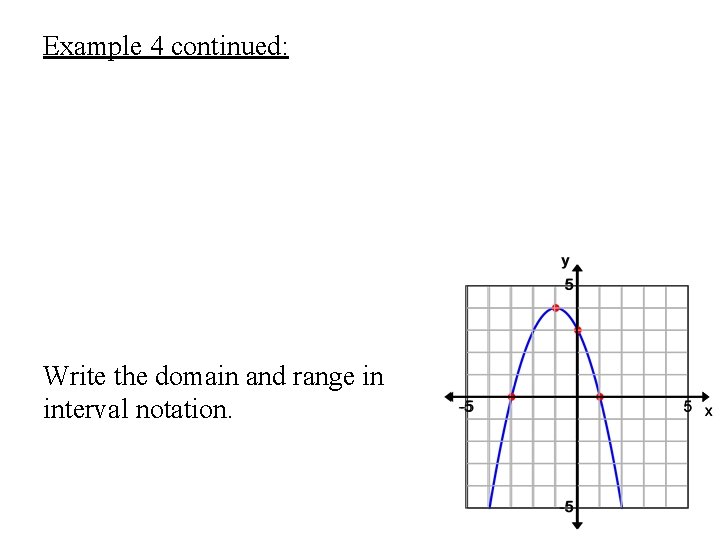
Example 4: Write in vertex form and graph the function. Identify the vertex, x- and y-intercepts, and axis of symmetry.

Example 4 continued: Write the domain and range in interval notation.

Write f(x) = ax 2 + bx + c (a ≠ 0) in Vertex Form Given a quadratic function defined by

Find the Vertex of a Parabola by Using the Vertex Formula For , the x-coordinate of the vertex is given by . To find the y-coordinate, evaluate The vertex is given by . .

Example 5: Given determine the vertex by using the vertex formula and by writing in vertex form.

Example 5 continued:

Example 6: At the end of his career, Sherlock Holmes retired to small farm in the country and took up a hobby of beekeeping. Being of an analytical mind, he could not just watch a bee fly from flower to flower, he formulated a mathematic model for the parabolic path the bee follows from flower A to flower B. The path is given by where x is the distance in inches along the ground from Sherlock.

Example 6 continued: a. What is the maximum height the bee reaches as it flies from A to B?

Example 6 continued: b. How far away from Sherlock are flowers A and B?

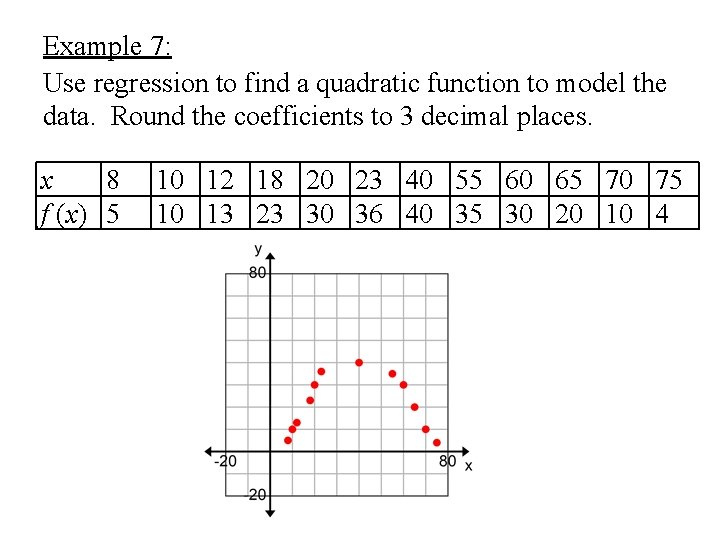
Example 7: Use regression to find a quadratic function to model the data. Round the coefficients to 3 decimal places. x 8 f (x) 5 10 12 18 20 23 40 55 60 65 70 75 10 13 23 30 36 40 35 30 20 10 4

Example 7 continued: 1. Use the STAT button, then EDIT to enter the x and y data in two lists. Exit this screen.

Example 7 continued: 2. Use the STAT button, then CALC, choose 5: Quad. Reg.

Example 7 continued: 3. Hit ENTER. Then CALCULATE. The equation is:

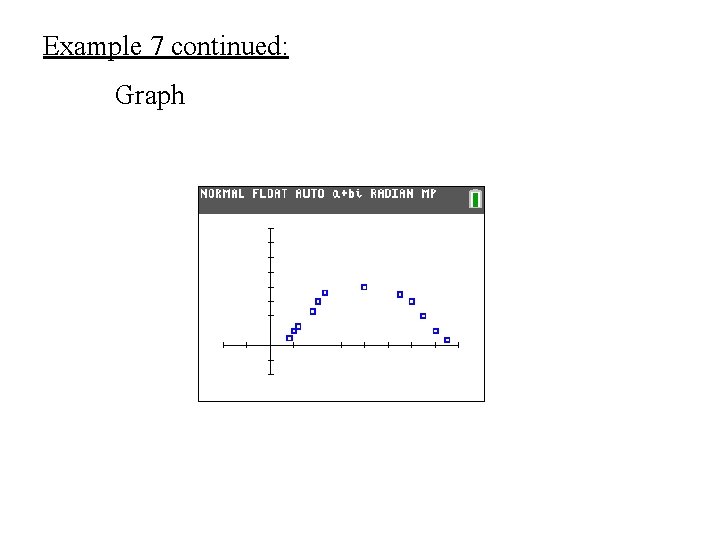
Example 7 continued: 4. To see the data and the line graphed: Above the y = key, select STATPLOT. Turn Plot 1 ON and select the type of graph.

Example 7 continued: Graph

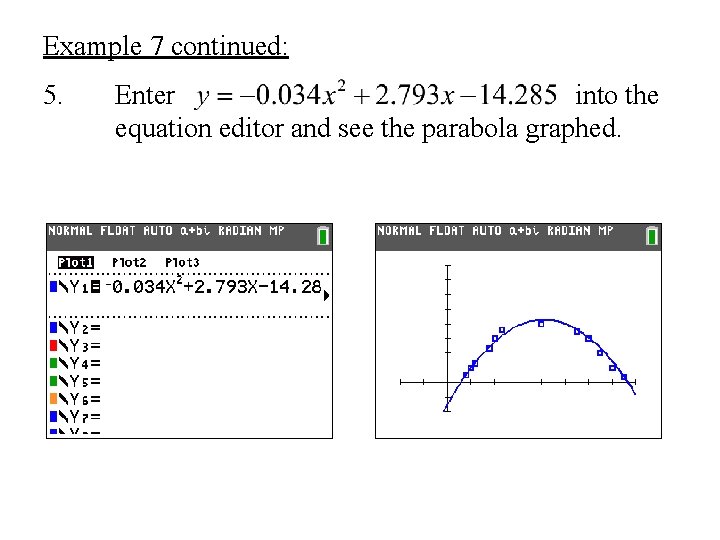
Example 7 continued: 5. Enter into the equation editor and see the parabola graphed.

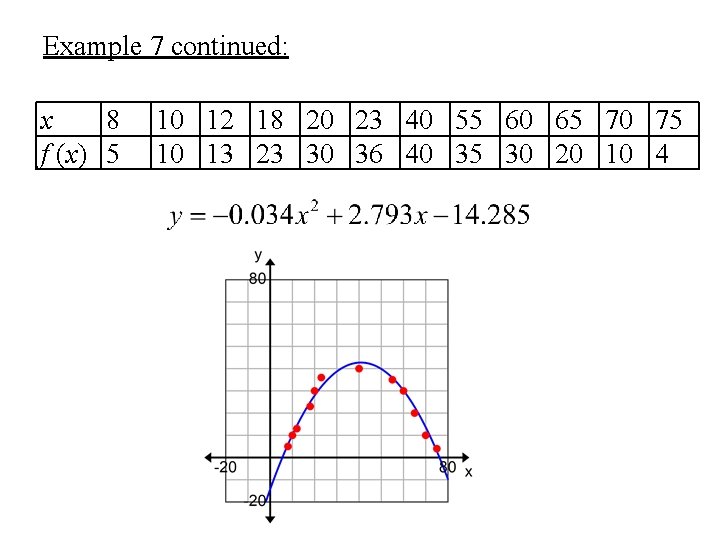
Example 7 continued: x 8 f (x) 5 10 12 18 20 23 40 55 60 65 70 75 10 13 23 30 36 40 35 30 20 10 4