Quadratic Functions A Quadratic Function is an equation















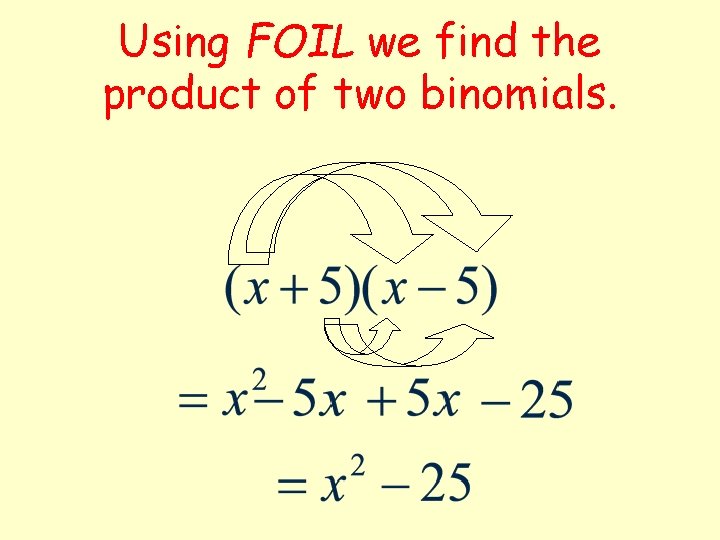
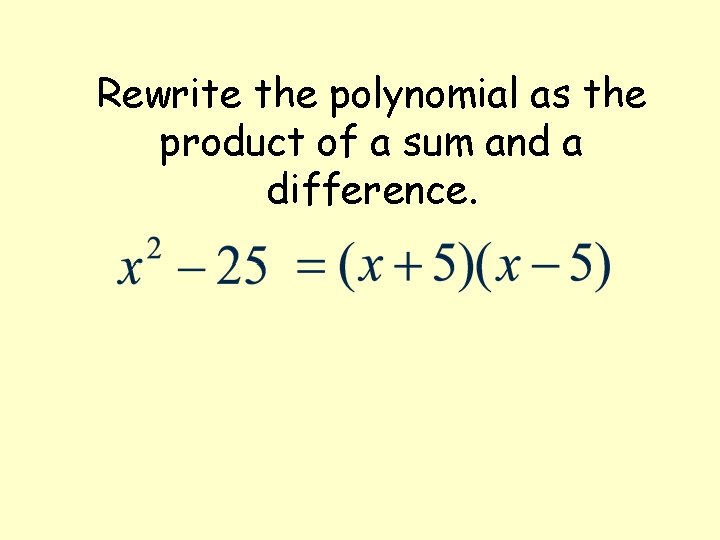




- Slides: 24

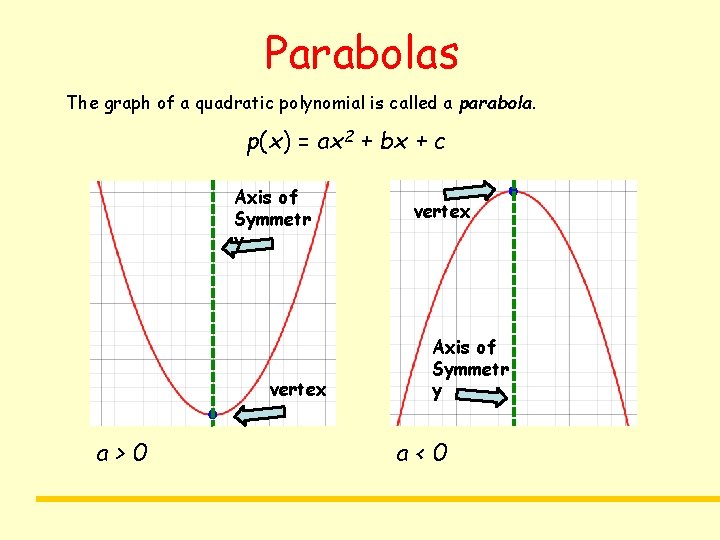
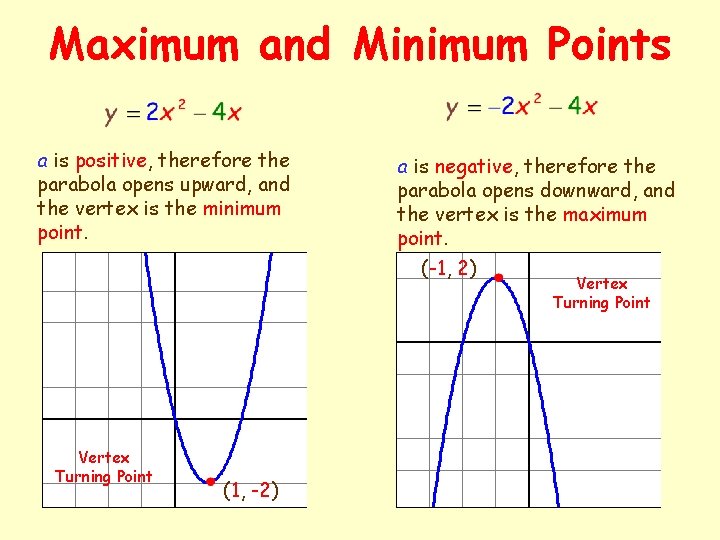
Quadratic Functions A Quadratic Function is an equation that has the form The graph of a Quadratic Equation is a u-shaped curve called a Parabola. The Vertex is the highest or lowest point of the parabola. The Vertex is also called the Turning Point. If a is positive, the parabola opens upward, and the vertex is the minimum point. If a is negative, the parabola opens downward, and the vertex is the maximum point. Maybe we should look at some diagrams.

Quadratic Functions A polynomial of degree 0 is called a constant function. A polynomial of degree 1 is called a linear function. Definition: A degree 2 polynomial function is called a quadratic function. The general form a quadratic function is p(x) = ax 2 + bx + c where a, b, and c are real numbers with a ≠ 0. Quadratic functions are incredibly important functions that show up everywhere in the real world.

Parabolas The graph of a quadratic polynomial is called a parabola. p(x) = ax 2 + bx + c Axis of Symmetr y vertex a>0 vertex Axis of Symmetr y a<0

Quadratic Functions • Function: • Standard Form (Vertex Form): • Graphs a parabola • All are symmetric to a line called the axis of symmetry (AOS)

Maximum and Minimum Points a is positive, therefore the parabola opens upward, and the vertex is the minimum point. a is negative, therefore the parabola opens downward, and the vertex is the maximum point. (-1, 2) Vertex Turning Point (1, -2) Vertex Turning Point

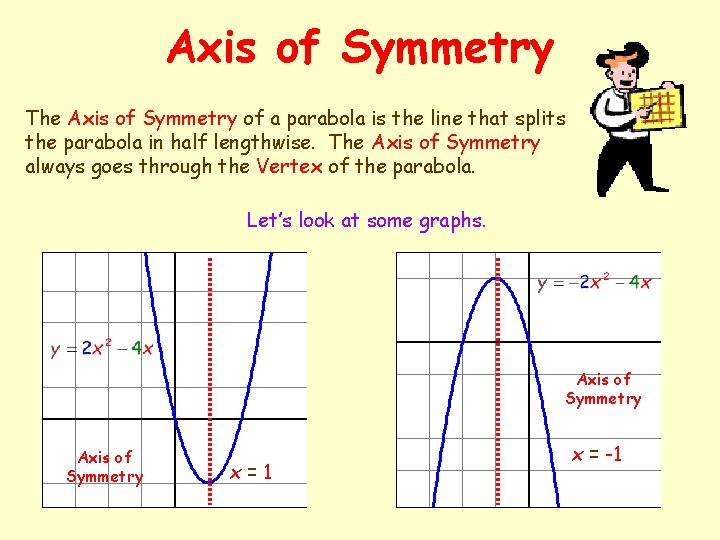
Axis of Symmetry The Axis of Symmetry of a parabola is the line that splits the parabola in half lengthwise. The Axis of Symmetry always goes through the Vertex of the parabola. Let’s look at some graphs. Axis of Symmetry x=1 x = -1

Finding the Axis of Symmetry You can find the Axis of Symmetry of any quadratic equation by using the formula Let’s take a look at those equations again. a = 2, b = -4, c = 0 vertex (1, -2) To find the coordinates of the vertex, plug the value of x into the original function. a = -2, b = -4, c = 0 vertex (-1, 2)

Using a Graphing Calculator to find the Axis of Symmetry First, let’s use the formula to find the axis of symmetry algebraically. Now let’s use the calculator to find the axis of symmetry graphically. vertex Enter the equation in Y 1 of the Y = window. View the graph by pressing Press 2 nd CALC 3 GRAPH (2, -1) Now push the easy button. (minimum) Move the curser slightly to the left of the vertex and press ENTER Move the curser slightly to the right of the vertex and press ENTER Press ENTER The calculator calculates the coordinates of the vertex.

Solving Quadratic Equations When you solve a quadratic equation, the x values that you calculate are referred to as the roots of the equation. When a quadratic function is in the form of , the roots can be found by setting the equation equal to zero and solving. When a quadratic equation is factorable, then it can be solved algebraically. Sometimes, the roots of the equation are referred to as the solution set. This is actually pretty easy. Let’s look at some examples.

Factoring Method #3 Factoring a trinomial in the form:

Factoring a trinomial: 1. Write two sets of parenthesis, ( )( ). These will be the factors of the trinomial. 2. Product of first terms of both binomials must equal first term of the trinomial.

Factoring a trinomial: 3. The product of last terms of both binomials must equal last term of the trinomial (c). 4. Think of the FOIL method of multiplying binomials, the sum of the outer and the inner products must equal the middle term (bx).

Factoring and Solving Quadratic Equations Find the solution set of the following quadratic functions. Rewrite the equation in ax 2 + bx + c = 0 format. Rewrite the equation so that a is positive. Factor the equation. Set each factor equal to zero and solve. Write the solution set.

Solving Quadratic Equations by Graphing Find the roots of the following quadratic function. 1) Enter the equation in Y 1. Let’s solve by factoring first. 2) View the graph by pressing 3) Press 2 nd CALC 2 GRAPH (zero) 4) Move the curser slightly to the left of the vertex and press ENTER Now let’s solve by graphing. 5) Move the curser slightly to the right of the vertex and press ENTER 6) Press ENTER The calculator calculates the 1 st root. Repeat steps 3 – 6 to calculate the 2 nd root.

More Solving Quadratic Equations by Graphing Approximate the roots of the following quadratic function to the nearest hundredth. Set equation equal to zero. This equation is unfactorable, so we have to use our calculator. 1) Enter the equation in Y 1. 2) View the graph by pressing GRAPH 3) Press 2 nd CALC 2 (zero) 4) Move the curser slightly to the left of the vertex and press ENTER 5) Move the curser slightly to the right of the vertex and press ENTER 6) Press ENTER The calculator calculates the 1 st root. Repeat steps 3 – 6 to calculate the 2 nd root. Round off your answer.

Solving Quadratic Equations with no Middle Term Let’s check with our calculator to make sure Since there is no middle term, this the roots are correct. equation is unfactorable. Approximate the roots of the following quadratic function to the nearest hundredth. That was easy

Perfect Squares? Squares Perfect Squares 1 4 9 16 25 36 49 64 81 100

Factoring: Difference of Squares • Count the number of terms. Is it a binomial? • Is the first term a perfect square? • Is the last term a perfect square? • Is it, or could it be, a subtraction of two perfect squares? x 2 – 9 = (x + 3)(x – 3) • The sum of squares will not factor a 2+b 2
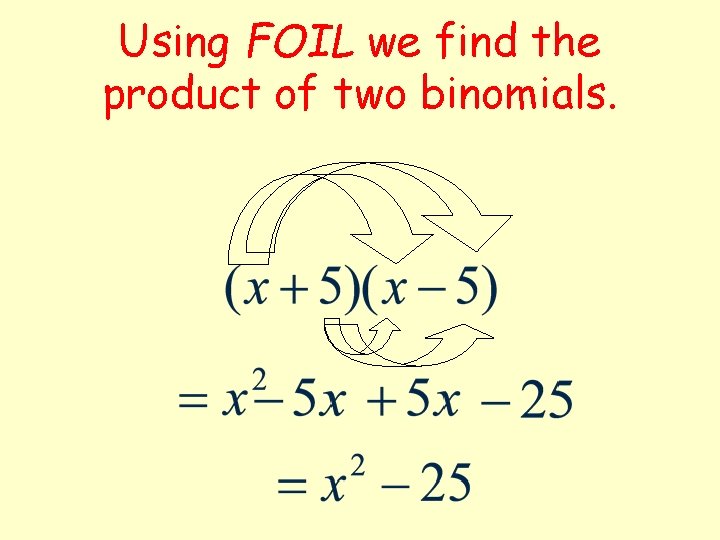
Using FOIL we find the product of two binomials.
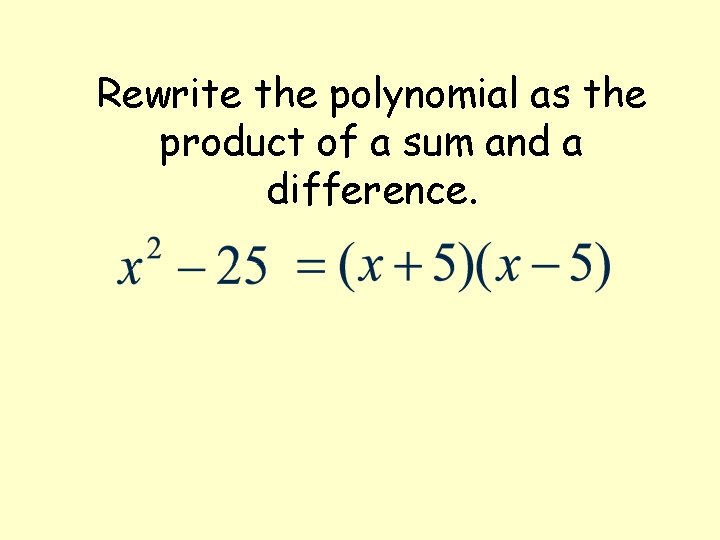
Rewrite the polynomial as the product of a sum and a difference.

Conditions for Difference of Squares • Must be a binomial with subtraction. • First term must be a perfect square. (x)(x) = x 2 • Second term must be a perfect square (6)(6) = 36

Check for GCF. Sometimes it is necessary to remove the GCF before it can be factored more completely.

Removing a GCF of -1. In some cases removing a GCF of negative one will result in the difference of squares.

Difference of Squares You Try