Quadrados Mnimos Situao w Em diversas cincias com

Quadrados Mínimos

Situação w Em diversas ciências com uma dimensão experimental, é necessário modelizar os fenômenos a partir de tabelas de dados experimentais. w A modelização consista em inúmeros casos em procurar a função que expressa melhor a relação entre os dados.

Problema w O objetivo do método de mínimos quadrados é determinar uma função, a partir de combinação linear de funções simples, que aproxima um conjunto de pontos. w Existem métodos polinomiais (aproximação com polinômio), mas elas não sempre fornecem aproximações aceitáveis. O método de mínimos quadrados permite estender as aproximações com funções não polinomiais.

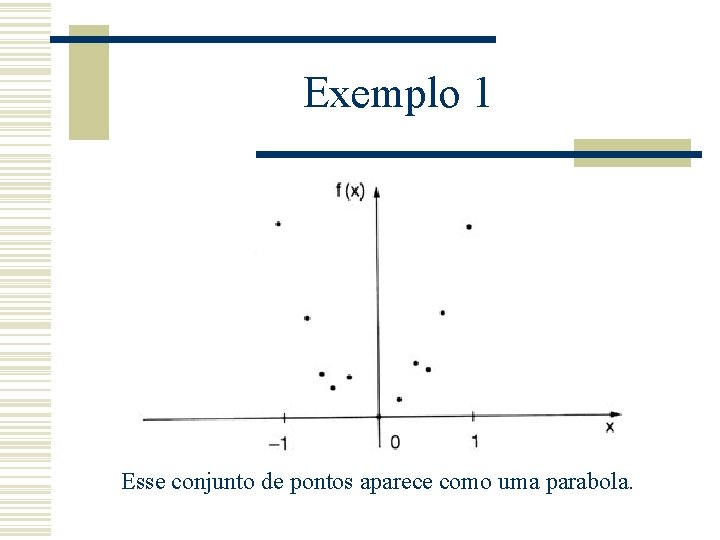
Exemplo 1 Esse conjunto de pontos aparece como uma parabola.

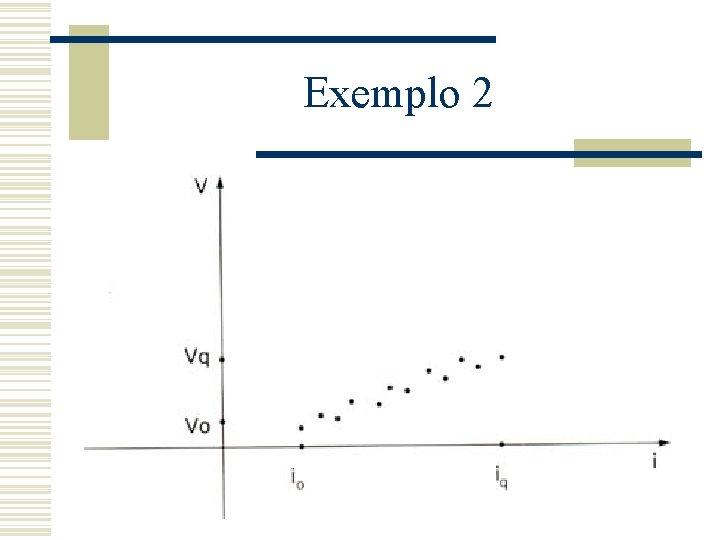
Exemplo 2

Caso discreto w A partir de uma tabela de valores (discretas), que representam vários pontos de uma função teórica (f(x)), tentamos determinar uma função j(x) combinação linear de funções gi(x) (j(x)=a 1 g 1(x)+. . . +angn(x)) de tal forma que o desvio de j - f seja mínimo para os valores da tabela. w O que significa mínimo nesse caso?

Caso contínuo w No caso contínuo, dada uma função f(x) contínua no intervalo [a, b] e escolhidas as funções g 1(x), . . , gn(x), o objetivo é determinar constantes a 1, . . . , an de tal forma que j(x)=a 1 g 1(x)+. . . +angn(x) se aproxima ao maximo de f(x) no intervalo [a, b]. w O que significa aproximar nesse caso?

Método dos quadrados mínimos w Caso discreto n n Considerando um conjunto de valores {(x 1, f(x 1)), . . . , {(xm, f(xm))} e n (com n£m) funções gn(x), o objetivo é encontrar um conjunto de coeficientes a 1, . . , an de tal forma que a função j(x)=a 1 g 1(x)+. . +angn(x) se aproxima ao máximo de f(x). O criterio para decidir da aproximação é minimizar a soma dos quadrados da diferencia entre as duas funções nos xi ou seja minimizar:

Método dos quadrados mínimos w Caso discreto n n Minimizar é minimizar a função: Para minimizar essa função F, devemos encontrar os pontos críticos da função, ou seja os valores (a 1, . . . , an) tal que:

Método dos quadrados mínimos w Caso discreto Elemento de calculo: Para derivar, considerando os termos com ai:

Método dos quadrados mínimos w Caso discreto Elemento de calculo:

Método dos quadrados mínimos w Caso discreto Com a condição: obtemos assim o sistema a resolver: n

Método dos quadrados mínimos w Caso discreto n n n As equações desse sistema são chamadas equações normais. Ele pode ser escrito: Onde e A matriz desse sistema é simétrica.

Método dos quadrados mínimos w Caso discreto n Considerando os vetores e e o produto escalar de dois vetores: Os coeficientes aij podem ser escritos: e b i: Demontra-se que se as funções g 1(x), . . . , gn(x) forem tais que os vetores: sejam linearmente independentes, o sistema admite uma solução única. Demonstra-se também que esta solução é o ponto em que a função F atinge seu valor mínimo.

Método dos quadrados mínimos w Caso discreto n Se os vetores tiverem a propriedade suplementar seguinte: , nesse caso os vetores são ortogonais entre si e a matriz A do sistema é diagonal. Exemplo de funções ortogonais: seria de Fourier (aproximação de funções periódicas), polinômios de Legendre, Gram, Chebyshev.

Método dos quadrados mínimos w Caso contínuo n Para aproximar uma função em um intervalo [a, b] com j uma combinação linear de funções (g 1, . . . , gn) de coeficientes (a 1, . . . , an), o método de quadrados mínimos propõe de minimizar a área entre as curvas duas funções, ou seja minimizar:

Método dos quadrados mínimos w Caso contínuo n Aplicando o mesmo princípio que no caso discreto, trata-se de minimizar a função: Obtemos um sistema de equações lineares: Aa=b, onde A=(aij), a=(a 1, . . . , an) e b=(b 1, . . . , bn). aij=<gi, gj> e bi=<f, gi> com n

Método dos quadrados mínimos w Caso não linear n n Existem casos que precisam ser aproximados por funções que não são resultados de combinação linear de funções simples. Por exemplo, podemos precisar de aproximar uma função com:

Método dos quadrados mínimos w Caso não linear n n n Para resolver o caso não linear, é necessário linear a função escolhida para a aproximação. No caso de , se queremos aproximar f(x) com essa função, podemos tentar aproximar ln(f(x)) com , ou seja , que é um caso linear. É importante notar que os parâmetros obtidos não são ótimos em relação com o critério de quadrados mínimos.

Método dos quadrados mínimos w Teste de alinhamento n Uma vez a função não linear em a 1, . . , an escolhida, para testar se ela é um bom escolhe podemos: Linearizar essa função, l Fazer o diagramo de dispersão dos novos dados l E observar se os pontos do diagramo estiverem alinhados. l

Exercício A tabela abaixo mostra as alturas e pesos de uma amostra de nove homens entre as idades de 25 e 29 anos, extraída ao acaso entre funcionários de uma grande indústria: Altura 183 173 168 188 158 163 193 163 178 cm Peso a) b) c) 79 69 70 81 61 63 79 71 73 Faça o diagrama de dispersão dosdados e observer que parece existir uma relação linear entre a altura e o peso. Ajuste a reta que descreva o comportamento do peso em função da altura, isto é peso=f(altura), e ajuste a reta que descreva o comportamento da altura em função do peso, isto é altura=f(peso). Estime o peso de um funcionário com 175 cm de altura; e estima a altura de um funcionário com 80 kg com cada uma das duas equações. kg

Solução b) 52. 7570 x-20. 0780 e 0. 0159+0. 6029 c) Com o primeiro ajuste: 1. 75 ->72. 2467 e 80 kg->1. 897 Com o segundo ajuste: 1. 75 ->72. 14 e 80 kg->1. 871

Exercício w Ajuste os dados: x y -8 -6 -4 -2 0 30 10 9 6 5 2 4 4 4 a) Usando a aproximação y» 1/(a 0+a 1 x). Faça o gráfico para 1/y e verifique esta aproximação é viável; b) Idem para y» abx; c) Compare os resultados

Solução w y=1/(0. 1958+0. 0185 x) w y=5. 5199(0. 8597)x