Qu es un conjunto n Un CONJUNTO es










































- Slides: 65

¿Qué es un conjunto? n Un CONJUNTO es una colección de objetos considerada como un todo. n Los objetos de un conjunto son llamados ELEMENTOS o miembros del conjunto. n Los elementos de un conjunto pueden ser cualquier cosa: números, personas, letras, otros conjuntos, etc. n Los conjuntos se denotan por letras mayúsculas: A, B, C, etc. n Un conjunto no posee elementos repetidos. 1

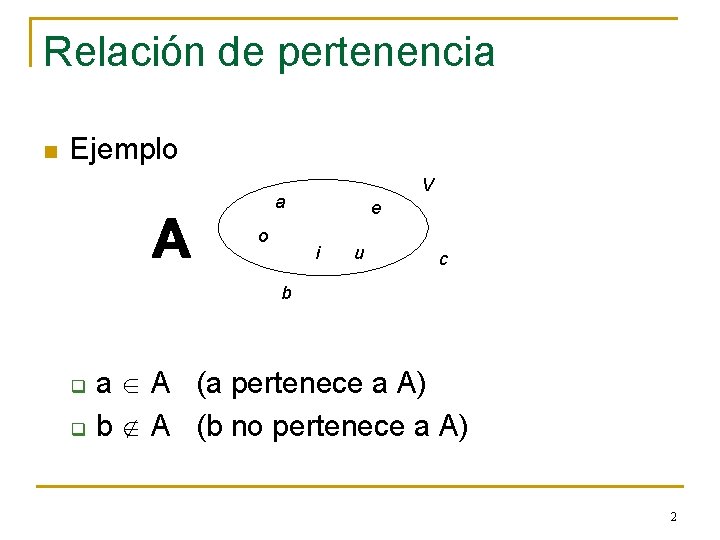
Relación de pertenencia n Ejemplo V a o e i u c b q q a A (a pertenece a A) b A (b no pertenece a A) 2

Formas de expresión de un conjunto n Para indicar un conjunto de utilizan llaves. { } n Hay distintas formas de expresarlo q q Enumerando sus elementos A = {a, e, i, o, u} Indicando alguna caracterización de sus elementos A = { x / x es una vocal } Tal que 3

Conjunto vacío n Es aquel que no contiene elementos n Representación: Ejemplo: n o {} B = { x / x un numero primo múltiplo de 5} B es un conjunto que no contiene elementos dado que ningún número PRIMO puede ser múltiplo de 5 B = {} 4

Cardinalidad de un conjunto n n Se refiere a la cantidad de elementos que contiene un conjunto Ejemplo: La cardinalidad de A = { x / x es una vocal } es 5 La cardinalidad de B = { x / x N ^ 2 x = 1} es 0 n Un conjunto puede contener infinitos elementos. 5

Igualdad de conjuntos n n Dos conjuntos son iguales si ambos tienen los mismos elementos o si ambos son vacíos Dados los conjuntos q q q A = { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 } B = { x / x es un numero digito} C = { x: x es de una sola cifra } A=B? A=C? 6

Subconjuntos de un conjunto n n Si A y B son conjuntos tales que todo elemento de B es también elemento de A, diremos que q B es un subconjunto PROPIO de A q B es una parte de A q B está incluido A. B A Esto se simboliza como B A 7

Subconjuntos de conjuntos n Dados los conjuntos q q q n n A={0, 3} B = { x / x (x – 3) = 0 } C = { x / x (x – 3) (x – 1) = 0 } A C C A pues 1 C y 1 A. 8

Conjunto de partes de un conjunto n Si A es un conjunto, llamaremos el conjunto de partes de A, al conjunto formado por todos los subconjuntos de A, y lo denotaremos P(A). n En otras palabras: P(A) = { B / B A } 9

Conjunto de partes de un conjunto n Ejemplos q q A = {1} P(A) = { {}, {1} } A tiene 1 elemento P(A) tiene 2 elementos A = {1, 2} P(A) = { { }, {1}, {2}, {1, 2} } A tiene 2 elementos P(A) tiene 4 elementos 10

Operaciones de conjuntos n Existen varias formas de obtener nuevos conjuntos a partir de otros existentes: q Unión q Intersección q Diferencia q Complemento 11

Operaciones de Conjuntos UNION A B = {x / x A x B } 12

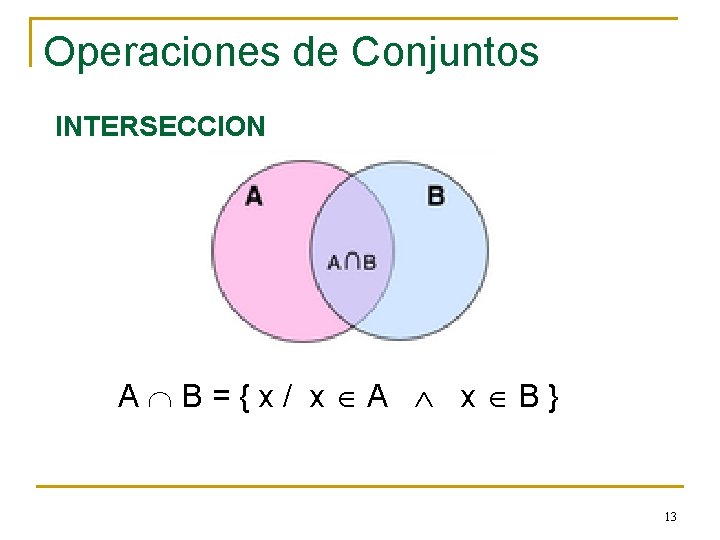
Operaciones de Conjuntos INTERSECCION A B={x/ x A x B} 13

Operaciones de Conjuntos DIFERENCIA B – A = {x / x B x A } 14

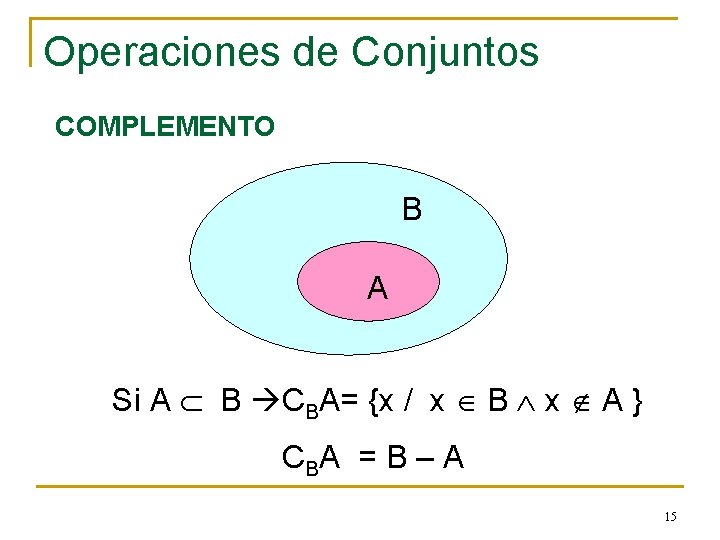
Operaciones de Conjuntos COMPLEMENTO B A Si A B CBA= {x / x B x A } CB A = B – A 15

Ejercicios n Dados los conjuntos A = { 1, 2, 3} , B = {1, 2, 4, 5} y C = { 2, 3, 4} Calcular q A B = { 1, 2 } q A B = { 1, 2, 3, 4, 5 } q A – B = { 3 } q B – A = { 4, 5 } q A B C = { 2 } q A – ( B – C) = { 2, 3 } 16

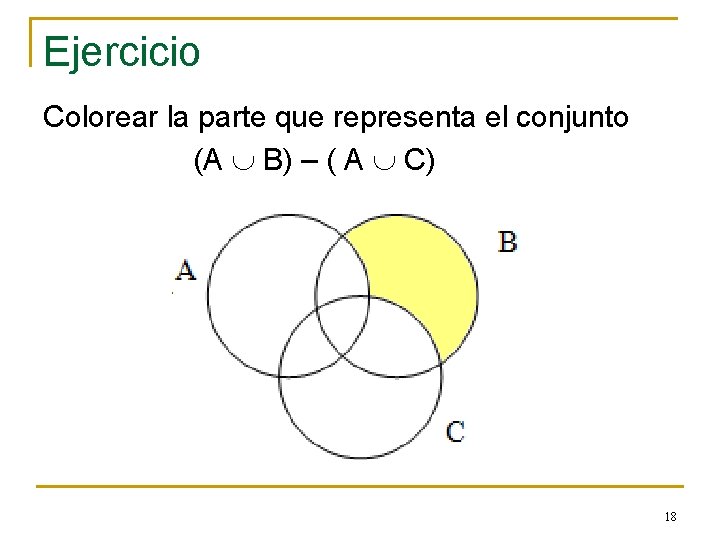
Ejercicio Colorear la parte que representa el conjunto (A B) – ( A C) 17

Ejercicio Colorear la parte que representa el conjunto (A B) – ( A C) 18

Autoevaluación En esta dirección http: //sipan. inictel. gob. pe/internet/av/evaluteo. htm n hay una autoevaluación de conjuntos. 19

Producto Cartesiano n El producto cartesiano de dos conjuntos A y B, denotado A × B, es el conjunto de todos los posibles pares ordenados cuyo primer componente es un elemento de A y el segundo componente es un elemento de B. A × B = { (x, y) / x A ^ y B } 20

Producto Cartesiano n Ejemplo: Si A = { a , b , c } y B = { 1 , 2 } Ax. B = { (a, 1), (a, 2), (b, 1), (b, 2), (c, 1), (c, 2) } Note que A tiene 3 elementos B tiene 2 elementos A x B tiene 6 elementos. 21

Producto Cartesiano n Ejemplo: A = { oro, copa, basto, espada } B = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 } A x B = { (oro, 1), (oro, 2), …, (oro, 12), (copa, 1), (copa, 2), …, (copa, 12), …, (espada, 12) } Note que A tiene 4 elementos B tiene 12 elementos A x B tiene 48 elementos (todas las cartas del mazo) 22

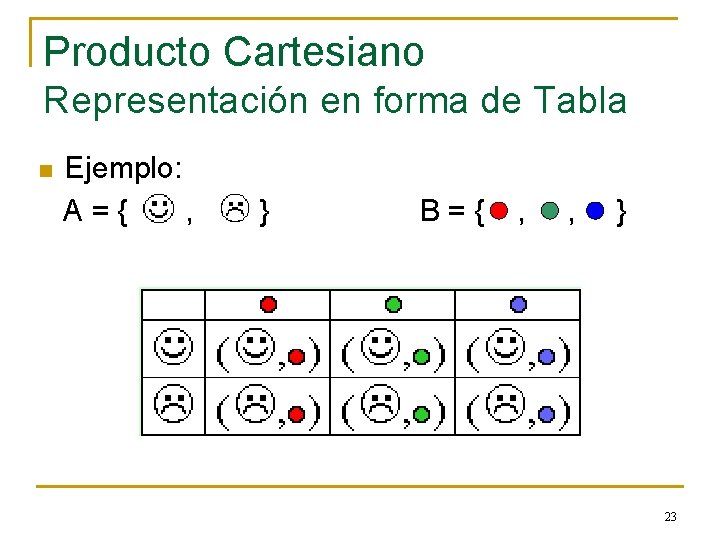
Producto Cartesiano Representación en forma de Tabla n Ejemplo: A={ , } B={ , , } 23

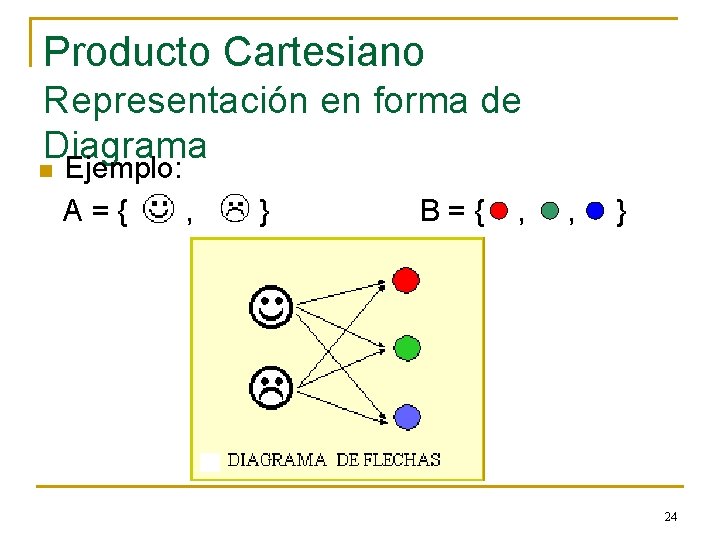
Producto Cartesiano Representación en forma de Diagrama n Ejemplo: A={ , } B={ , , } 24

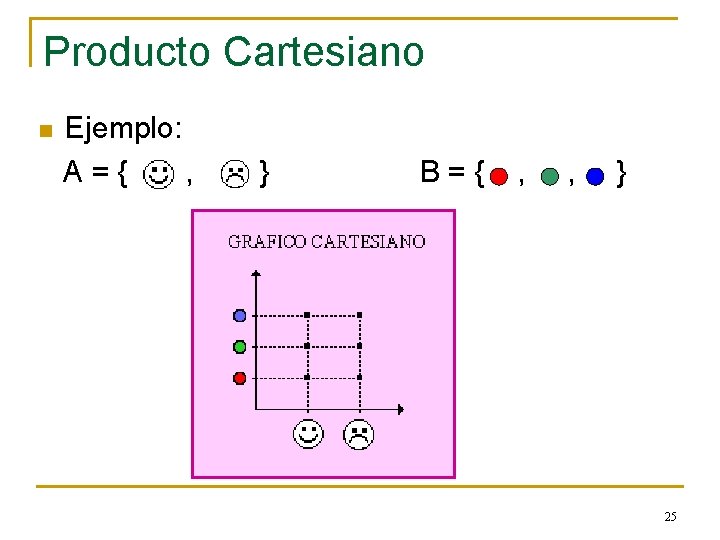
Producto Cartesiano n Ejemplo: A={ , } B={ , , } 25

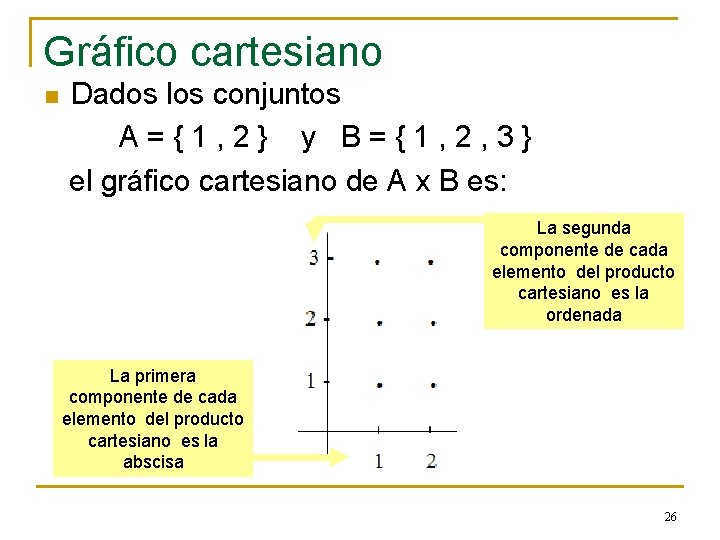
Gráfico cartesiano n Dados los conjuntos A={1, 2} y B={1, 2, 3} el gráfico cartesiano de A x B es: La segunda componente de cada elemento del producto cartesiano es la ordenada La primera componente de cada elemento del producto cartesiano es la abscisa 26

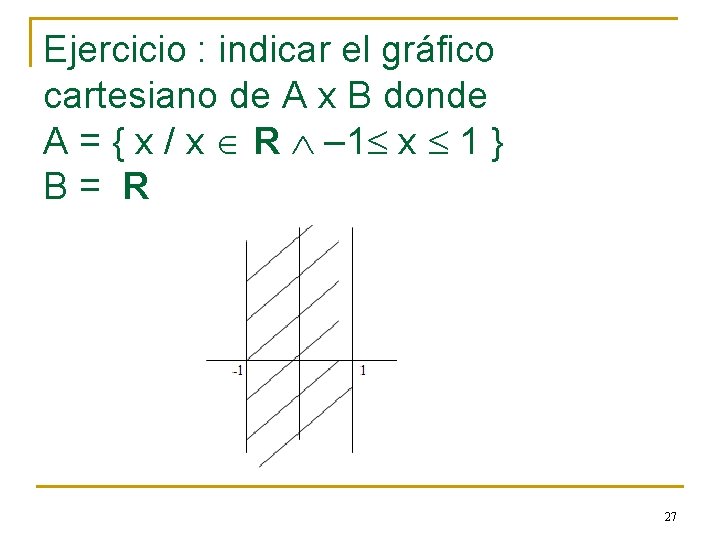
Ejercicio : indicar el gráfico cartesiano de A x B donde A = { x / x R – 1 x 1 } B= R 27

Ejercicio : indicar el gráfico cartesiano de A x B donde A={x/x R 2 x<5} B = { x / x R 1 < x 3} 28

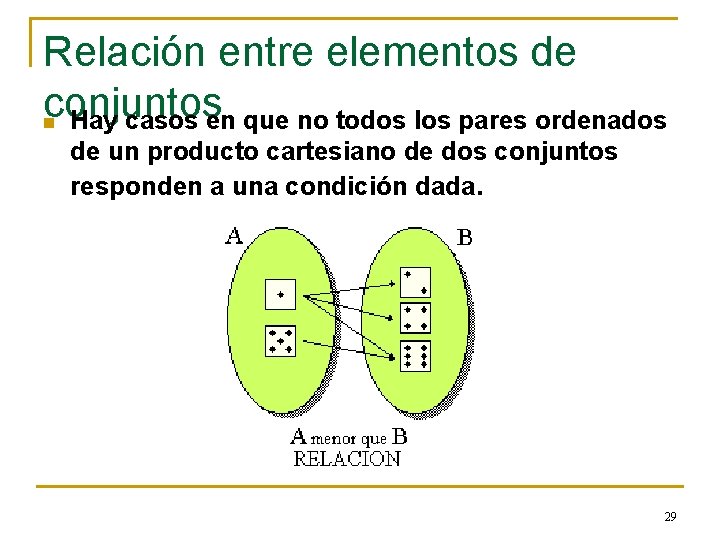
Relación entre elementos de conjuntos n Hay casos en que no todos los pares ordenados de un producto cartesiano de dos conjuntos responden a una condición dada. 29

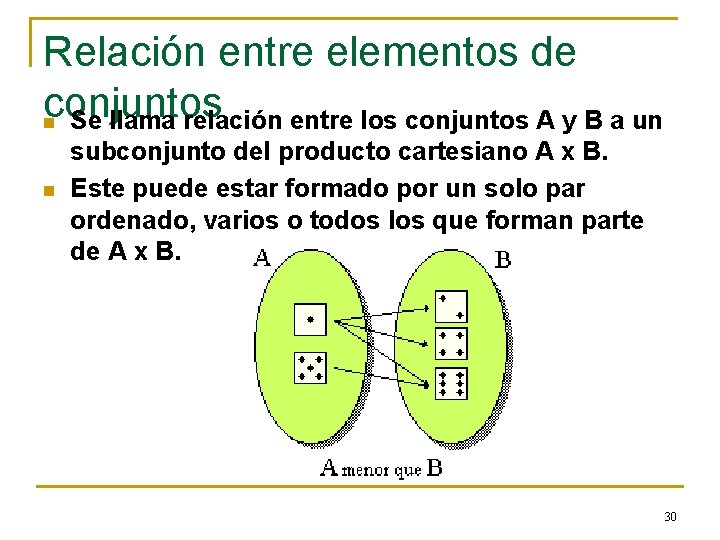
Relación entre elementos de conjuntos n Se llama relación entre los conjuntos A y B a un n subconjunto del producto cartesiano A x B. Este puede estar formado por un solo par ordenado, varios o todos los que forman parte de A x B. 30

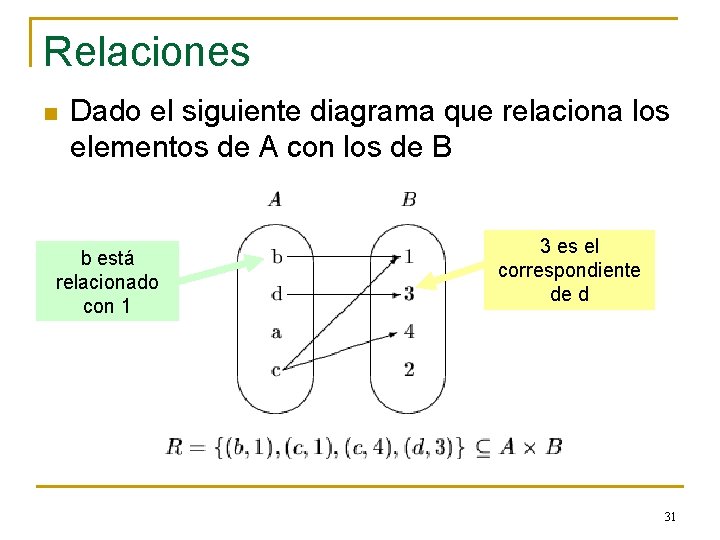
Relaciones n Dado el siguiente diagrama que relaciona los elementos de A con los de B b está relacionado con 1 3 es el correspondiente de d 31

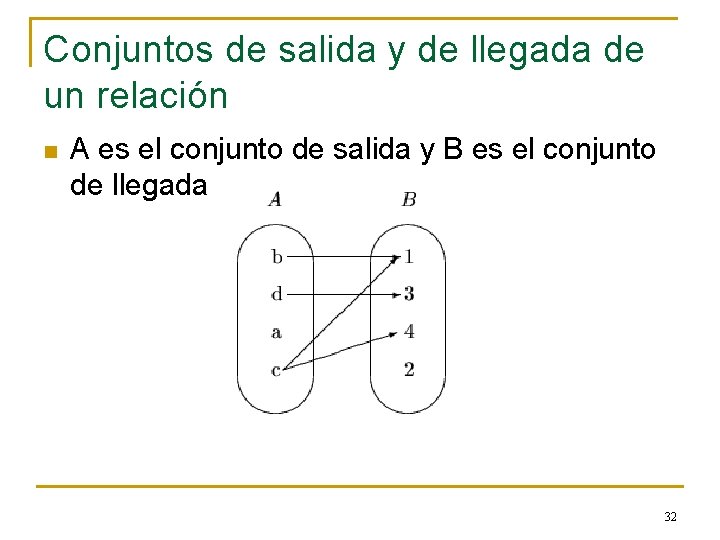
Conjuntos de salida y de llegada de un relación n A es el conjunto de salida y B es el conjunto de llegada 32

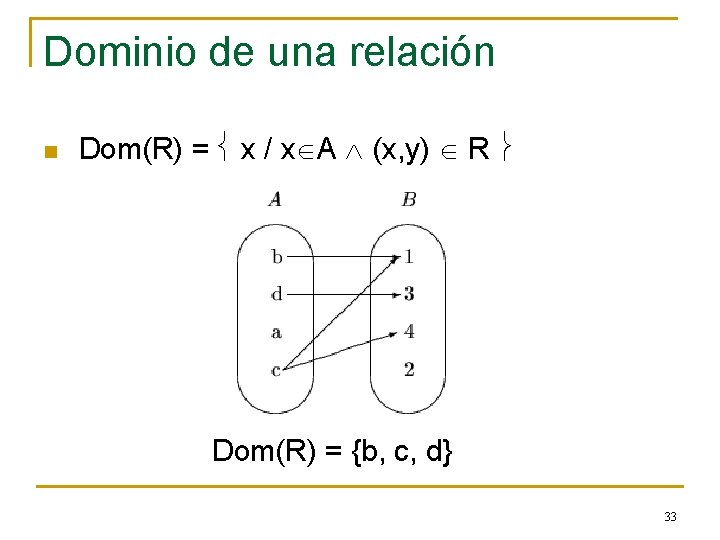
Dominio de una relación n Dom(R) = x / x A (x, y) R Dom(R) = {b, c, d} 33

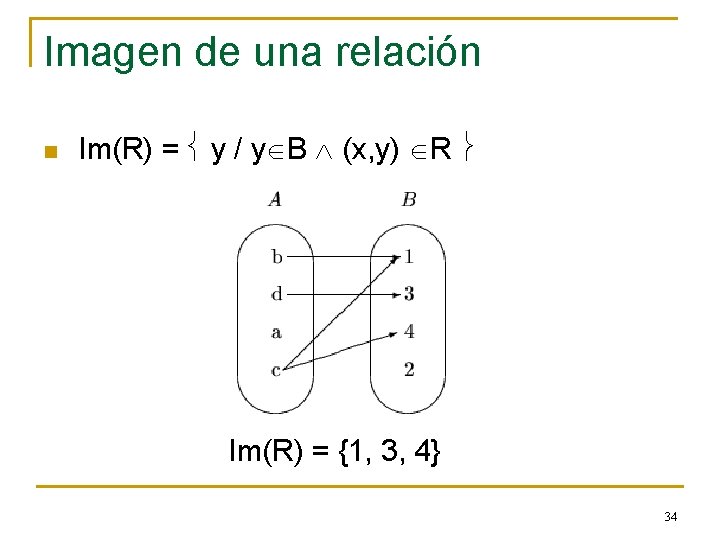
Imagen de una relación n Im(R) = y / y B (x, y) R Im(R) = {1, 3, 4} 34

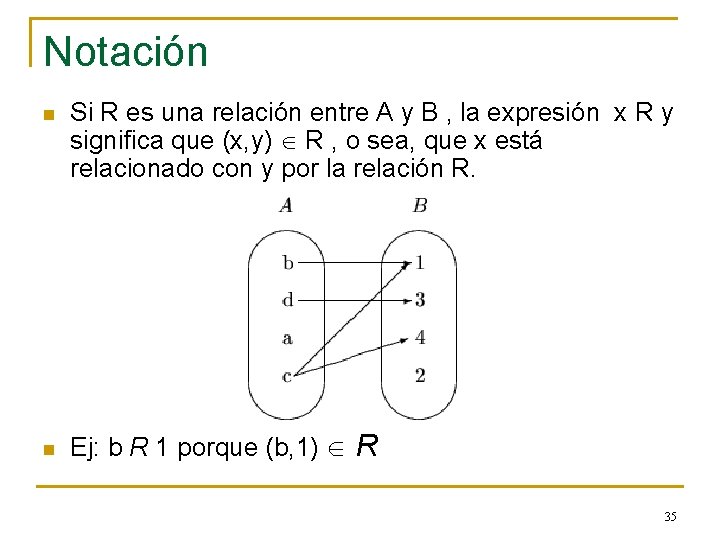
Notación n n Si R es una relación entre A y B , la expresión x R y significa que (x, y) R , o sea, que x está relacionado con y por la relación R. Ej: b R 1 porque (b, 1) R 35

Relación definida en un conjunto n Cuando los conjuntos de partida y de llegada de una relación R son el mismo conjunto A, decimos que R es una relación definida en A, o, simplemente, una relación en A. n Una relación R en A es entonces un subconjunto de A 2 = A x A 36

Relación definida en un conjunto n Ejemplo: Sea H = { x / x es un ser humano} y R la relación “es madre de” q q q R es una relación en H. Por qué? Como Ana es la madre de Luis, decimos que el par (Ana, Luis) R. Note que los pares que verifiquen R son un subconjunto de H x H. 37

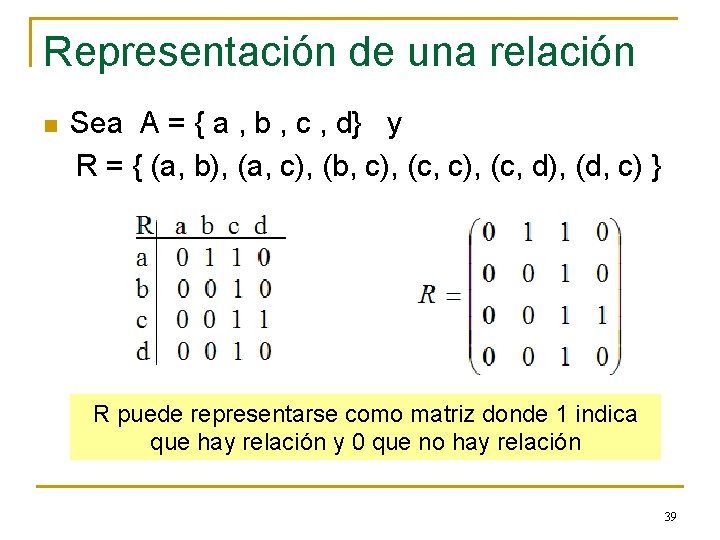
Representación de una relación n Sea A = { a , b , c , d} y R = { (a, b), (a, c), (b, c), (c, d), (d, c) } Los vértices del grafo son los elementos A y las aristas dirigidas representan los elementos de R Para poder construir el grafo dirigido A debe contener un número finito de elementos 38

Representación de una relación n Sea A = { a , b , c , d} y R = { (a, b), (a, c), (b, c), (c, d), (d, c) } R puede representarse como matriz donde 1 indica que hay relación y 0 que no hay relación 39

Propiedades de las relaciones definidas en un conjunto n Si establecemos una relación entre los elementos de un mismo conjunto, existen cinco propiedades fundamentales que pueden cumplirse en esa relación n Propiedad reflexiva n Propiedad simétrica n Propiedad antisimétrica n Propiedad transitiva 40

Propiedad reflexiva n La propiedad reflexiva dice que todos los elementos de un conjunto están relacionados con si mismo R es reflexiva si para todo x A, el par (x, x) R 41

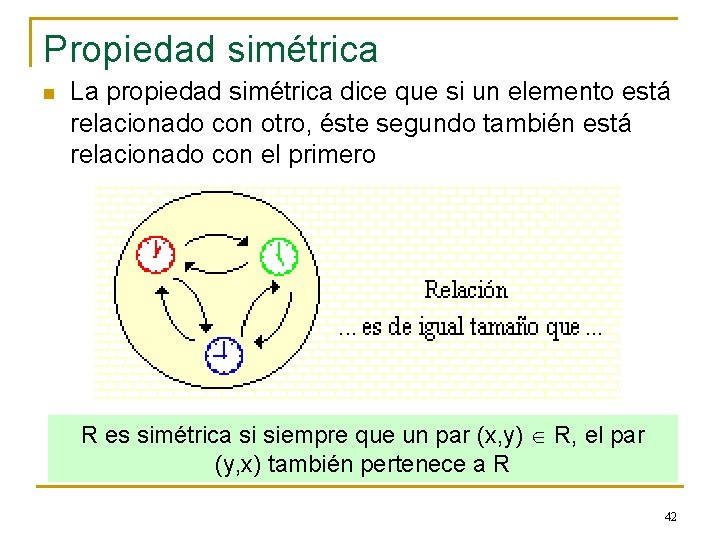
Propiedad simétrica n La propiedad simétrica dice que si un elemento está relacionado con otro, éste segundo también está relacionado con el primero R es simétrica si siempre que un par (x, y) R, el par (y, x) también pertenece a R 42

Propiedad Simétrica n Ejemplo q Dado A = {3, 4, 2} decir si las siguientes relaciones en A 2 son simétricas R = {(2, 3), (3, 4), (4, 3), (3, 2), (4, 4)} S = {(3, 2), (4, 3), (2, 2), (3, 4)} 43

Propiedad asimétrica n Una relación es asimétrica si ningún par ordenado de la relación cumple la propiedad simétrica. 44

Propiedad antisimétrica n Una relación es antisimétrica cuando sólo cumplen la propiedad simétrica los pares de elementos iguales y no la cumplen los pares formados por distintos elementos. 45

Propiedad antisimétrica n Ejemplo q Dado A = {2, 4, 6} decir si las siguientes relaciones en A 2 son antisimétricas R = {(2, 2), (4, 4)} S = {(2, 4)} T ={(4, 6), (2, 2), (6, 4), (4, 2)} 46

Propiedad transitiva n La propiedad transitiva dice que si un elemento está relacionado con otro y éste está a su vez relacionado con un tercero, el primer elemento está relacionado con el tercero. R es transitiva si x , y , z , (x, y) R (y, z) R (x, z) R 47

Propiedad transitiva n Ejemplo q Dado A = {2, 4, 6, 3} decir si las siguientes relaciones en A 2 son transitivas R = {(2, 2), (2, 3), (4, 6), (6, 2), (4, 3), (6, 3)} S = {(2, 2), (4, 4), (4, 2), (2, 6), (6, 4), (6, 2)} 48

Ejercicio n Dado A = {1, 2, 3} decir a que tipo pertenecen las siguientes relaciones q R 1 = {(1, 1), (2, 2), (3, 2), (2, 3), (3, 3)}. q R 2 = {(1, 1)}. q R 3 = {(1, 2)}. q R 4 = {(1, 1), (2, 3), (3, 2)}. 49

Ejercicio n Sea A = {2, 3, 4, 5, 6} R = {(x, y) / x A, y A, | x – y | es divisible por 3} n Escribir por extensión a R. 50

Casos especiales n Como casos especiales de las relaciones en un conjunto se define: q q Relaciones de orden: Permite ordenar los elementos a través de la relación. Relación de equivalencia: Permite marcar características similares entre los elementos de un conjunto 51

Relación de orden n n La relación de orden es aquella en que los elementos pueden ordenarse a través de la relación. Ejemplo 52

Relación de Orden n Pueden definirse dos tipos de relación: q Relación de orden amplio. q Relación de orden estricto. 53

Relación de orden amplio n Una relación de orden amplio es aquella que cumple las propiedades reflexiva, antisimétrica y transitiva. 54

Relación de orden amplio Ejemplo: R = “… es menor o igual que…” 55

Ejemplo: Indicar si las siguientes relaciones son de orden amplio n Sea A es el conjunto de los naturales y R = {(x, y) / x, y A ^ “x divide a y”} n Sea A es el conjunto de los subconjuntos de un conjunto dado y R = {(x, y) / x, y A ^ “x está incluído en y”} 56

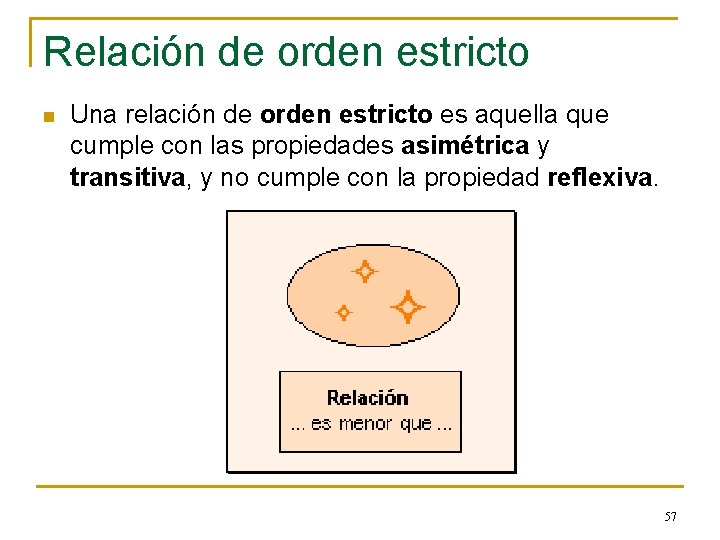
Relación de orden estricto n Una relación de orden estricto es aquella que cumple con las propiedades asimétrica y transitiva, y no cumple con la propiedad reflexiva. 57

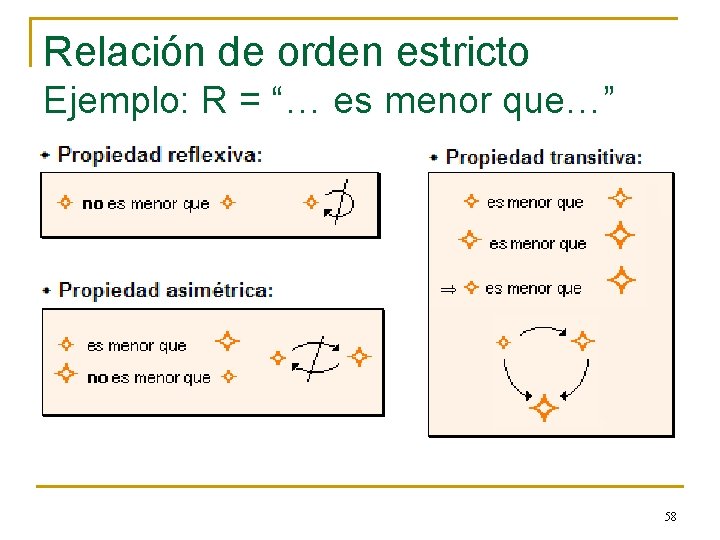
Relación de orden estricto Ejemplo: R = “… es menor que…” 58

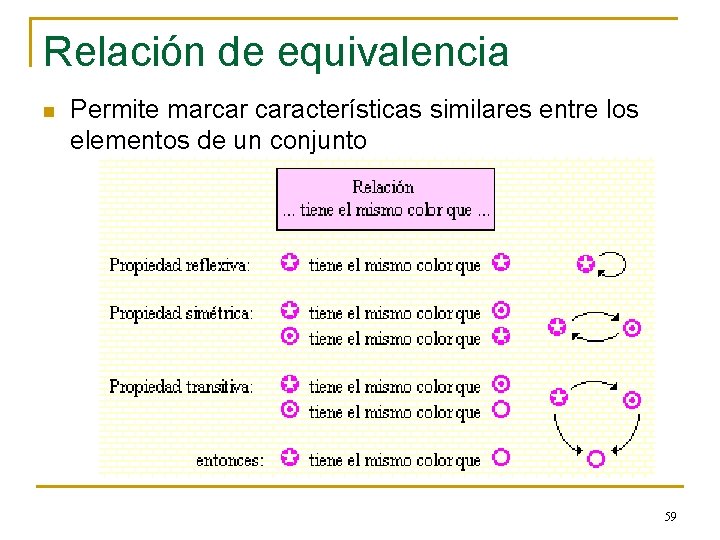
Relación de equivalencia n Permite marcar características similares entre los elementos de un conjunto 59

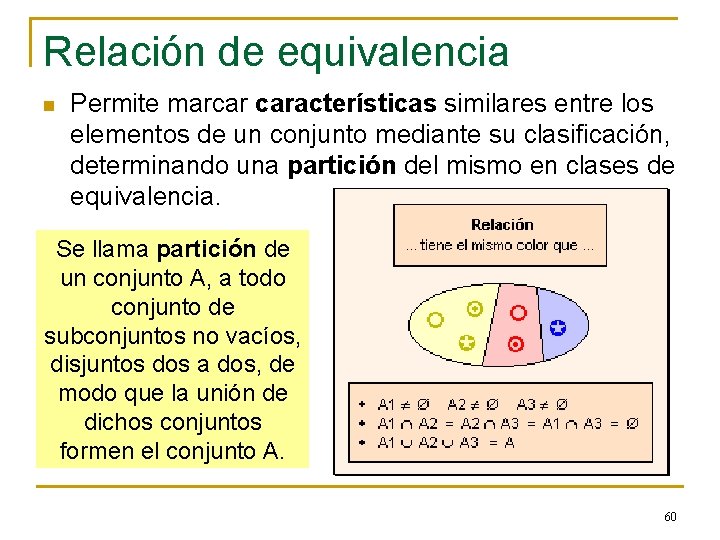
Relación de equivalencia n Permite marcar características similares entre los elementos de un conjunto mediante su clasificación, determinando una partición del mismo en clases de equivalencia. Se llama partición de un conjunto A, a todo conjunto de subconjuntos no vacíos, disjuntos dos a dos, de modo que la unión de dichos conjuntos formen el conjunto A. 60

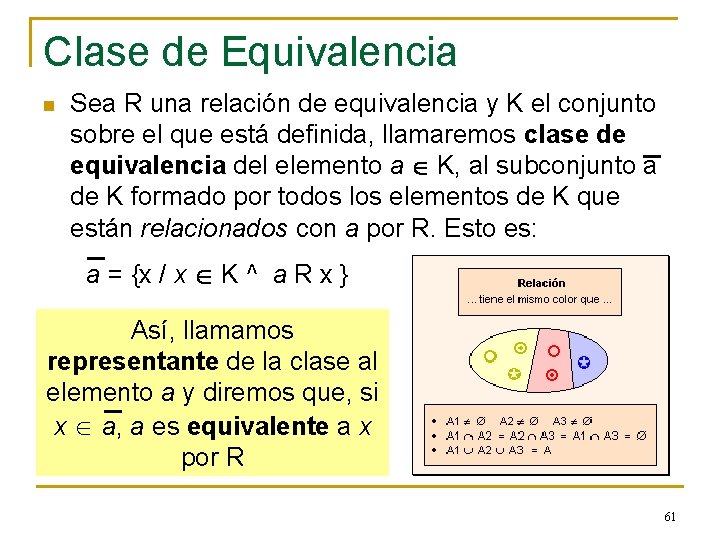
Clase de Equivalencia n Sea R una relación de equivalencia y K el conjunto sobre el que está definida, llamaremos clase de equivalencia del elemento a K, al subconjunto a de K formado por todos los elementos de K que están relacionados con a por R. Esto es: a = {x / x K ^ a R x } Así, llamamos representante de la clase al elemento a y diremos que, si x a, a es equivalente a x por R 61

Conjunto Cociente n Sea R una relación de equivalencia y K el conjunto sobre el que está definida, llamaremos conjunto cociente K por R y lo notaremos K/R a la partición de K formada por todas las clases de equivalencia determinadas en K dada R. Es decir, el conjunto cociente es el conjunto de todas las clases de equivalencia que se puedan formar con los elementos de K, dada R. 62

Ejemplo de Relación de Equivalencia n Sea H el conjunto formado por todos los seres humanos. R= {(x, y) / x, y H ^ "x es compatriota de y"} q q q R es reflexiva puesto que toda persona es compatriota de si mismo. R es simétrica, puesto que "si x es compatriota de y, y es compatriota de x". R es transitiva, por que "si x es compatriota de y es compatriota de z, entonces x es compatriota de z". 63

Ejemplo de Relación de Equivalencia n Sea H el conjunto formado por todos los seres humanos. R= {(x, y) / x, y H ^ "x es compatriota de y"} q q q Dado un elemento a de H, su clase de equivalencia estará formada por sus compatriotas. El conjunto cociente de H por R, H/R, es el conjunto formado por todas las clases de equivalencias. H/R es una partición de H. 64

Ejercicio n ¿ Cuál de las siguientes relaciones en S son de equivalencia? q q R = {(a, b)/ a y b tienen la misma madre}, donde S = {a / a es cualquier persona} S es el conjunto de números enteros y R es la relación “x es congruente con y módulo 2”, es decir, que x e y tienen el mismo resto al ser divididos por 2. 65
 Conjunto pode ser entendido intuitivamente
Conjunto pode ser entendido intuitivamente Pontos equidistantes
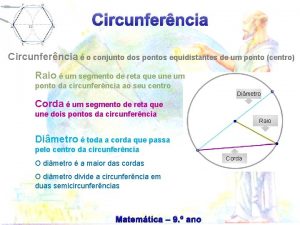
Pontos equidistantes Conjunto de procesos sistemáticos
Conjunto de procesos sistemáticos Reglamento conjunto 2019
Reglamento conjunto 2019 Conjunto convexo
Conjunto convexo Pastoral de conjunto
Pastoral de conjunto Ejemplos de conjuntos infinitos
Ejemplos de conjuntos infinitos Conjunto el buen samaritano
Conjunto el buen samaritano Diferencias finitas
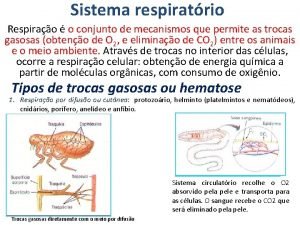
Diferencias finitas Concepto de ecosistema
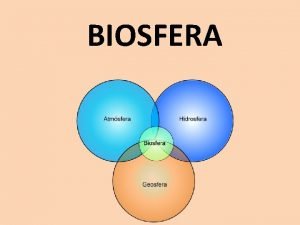
Concepto de ecosistema La biosfera es el conjunto de
La biosfera es el conjunto de Conjunto adidas virginia
Conjunto adidas virginia Referencias bibliograficas apa
Referencias bibliograficas apa La vida es un conjunto de momentos
La vida es un conjunto de momentos Que es un conjunto infinito
Que es un conjunto infinito Complementar de conjuntos
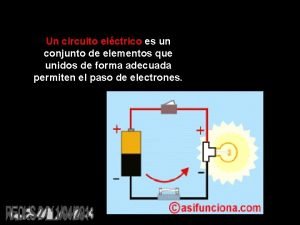
Complementar de conjuntos Resistencia total de un circuito mixto
Resistencia total de un circuito mixto Divisores de 24
Divisores de 24 Conjunto de programas
Conjunto de programas Conjunto de alabanzas y piropos a la virgen
Conjunto de alabanzas y piropos a la virgen Conjunto de identidades
Conjunto de identidades Conjunto de postulados
Conjunto de postulados Un enunciado puede ser un texto
Un enunciado puede ser un texto Dibujos de un de un
Dibujos de un de un Conjuntos arbitrarios
Conjuntos arbitrarios Que es un numero natural
Que es un numero natural Conjunto de circunstancias
Conjunto de circunstancias Ejemplos de conjuntos finitos
Ejemplos de conjuntos finitos Tiempo lavado de manos clinico
Tiempo lavado de manos clinico Conjunto de numeros enteros
Conjunto de numeros enteros O que é o conjunto universo
O que é o conjunto universo Reglamento conjunto 2019
Reglamento conjunto 2019 Es un conjunto de pasos
Es un conjunto de pasos Ejemplos de conjuntos comparables
Ejemplos de conjuntos comparables El conjunto de saberes que permiten fabricar objetos
El conjunto de saberes que permiten fabricar objetos Conjunto de obras literarias
Conjunto de obras literarias Casal é um nome coletivo
Casal é um nome coletivo Caracteristicas de conjuntos
Caracteristicas de conjuntos Pontos equidistantes
Pontos equidistantes Conjunto vazio
Conjunto vazio Ejemplos de conjuntos finitos
Ejemplos de conjuntos finitos Diagrama de venn con 3 conjuntos
Diagrama de venn con 3 conjuntos Liquidos seminales
Liquidos seminales Propiedad o conjunto de propiedades inherentes a una cosa
Propiedad o conjunto de propiedades inherentes a una cosa Conjunto formado por seres vivos
Conjunto formado por seres vivos Conjunto de medidas preventivas
Conjunto de medidas preventivas Tipos de biozonas
Tipos de biozonas Cuando un conjunto es subconjunto de otro
Cuando un conjunto es subconjunto de otro Conjuntos nulo
Conjuntos nulo Relaciones interespecificas ejemplos
Relaciones interespecificas ejemplos Quien narra la biblia
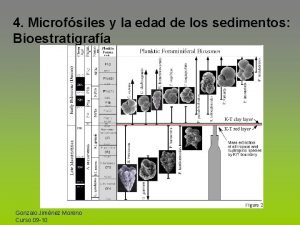
Quien narra la biblia Clase 4
Clase 4 Letanas
Letanas Trava lingua do mafagafinho
Trava lingua do mafagafinho Ordenar numeros enteros
Ordenar numeros enteros Conjunto dos números racionais
Conjunto dos números racionais Conjunto
Conjunto Ejemplo conjunto finito
Ejemplo conjunto finito Conjunto de prerrogativas
Conjunto de prerrogativas Mcd
Mcd Colectivo
Colectivo Cobre sustancia pura
Cobre sustancia pura Matematica numeros racionais
Matematica numeros racionais Cardinalidade dos conjuntos
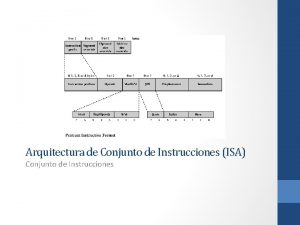
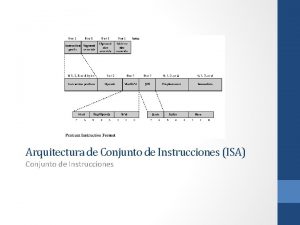
Cardinalidade dos conjuntos Arquitetura do conjunto de instruções (isa)
Arquitetura do conjunto de instruções (isa) Actividades interrelacionadas
Actividades interrelacionadas