Qu Cloud A New Qubit Mapping Mechanism for

Qu. Cloud: A New Qubit Mapping Mechanism for Multi-programming Quantum Computing in Cloud Environment Lei Liu, Xinglei Dou (Speaker) Sys-Inventor Lab, SKLCA, ICT, CAS IEEE HPCA-2021 (Session 2 B)

Executive Summary • Multi-programming in quantum computing cloud services has been proposed to improve throughput and resource utilization • Challenge: Multi-programming leads to degradation in fidelity and contention between concurrent quantum programs • Goal: To improve throughput and resource utilization while ensuring fidelity • Solutions: • Community Detection Assisted Partition (CDAP): Locate the robust resources for initial mapping • X-SWAP: Enable inter-program SWAPs for reducing compilation overheads • Compilation task scheduler: Fairness, trade-off between throughput and fidelity • Results: 9. 7% improvement in fidelity; 11. 6% reduction in compilation overheads

Outline q. Introduction q. Motivation q. Designs q. Evaluation q. Conclusion

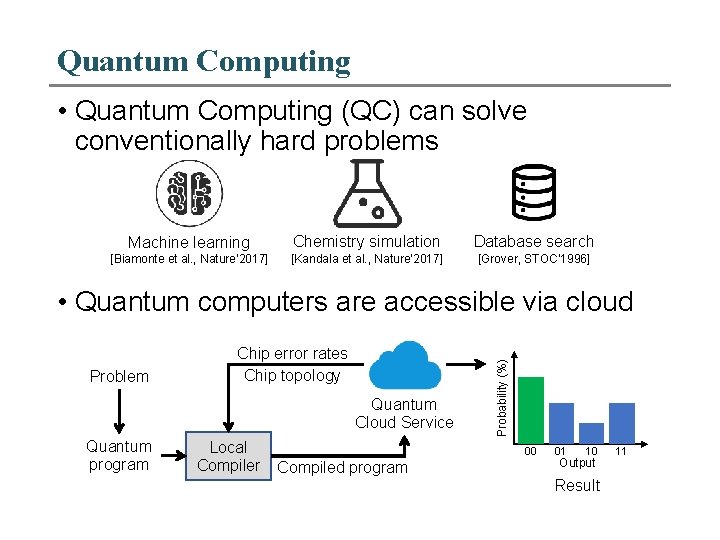
Quantum Computing • Quantum Computing (QC) can solve conventionally hard problems Machine learning Chemistry simulation Database search [Biamonte et al. , Nature’ 2017] [Kandala et al. , Nature’ 2017] [Grover, STOC’ 1996] Problem Chip error rates Chip topology Quantum Cloud Service Quantum program Local Compiler Probability (%) • Quantum computers are accessible via cloud 00 Compiled program 01 10 Output Result 11

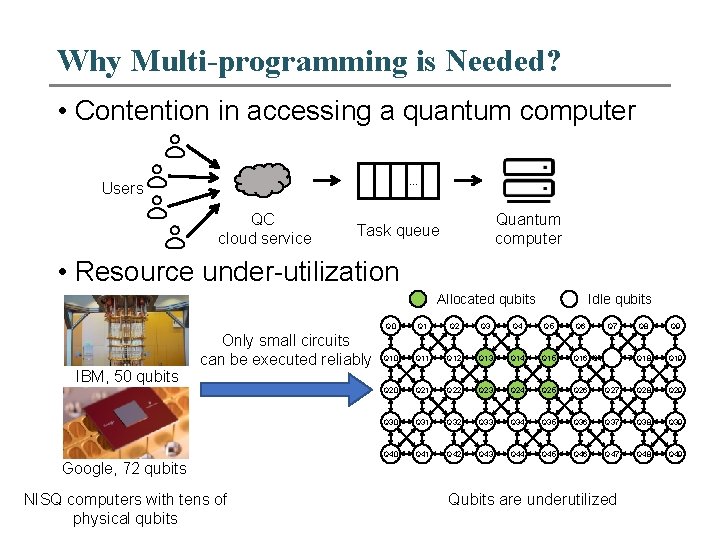
Why Multi-programming is Needed? • Contention in accessing a quantum computer … Users QC cloud service Quantum computer Task queue • Resource under-utilization Allocated qubits IBM, 50 qubits Only small circuits can be executed reliably Idle qubits Q 0 Q 1 Q 2 Q 3 Q 4 Q 5 Q 6 Q 10 Q 11 Q 12 Q 13 Q 14 Q 15 Q 16 Q 1 Q 20 Q 21 Q 22 Q 23 Q 24 Q 25 Q 26 Q 30 Q 31 Q 32 Q 33 Q 34 Q 35 Q 40 Q 41 Q 42 Q 43 Q 44 Q 45 Q 7 Q 8 Q 9 7 Q 18 Q 19 Q 27 Q 28 Q 29 Q 36 Q 37 Q 38 Q 39 Q 46 Q 47 Q 48 Q 49 Google, 72 qubits NISQ computers with tens of physical qubits Qubits are underutilized

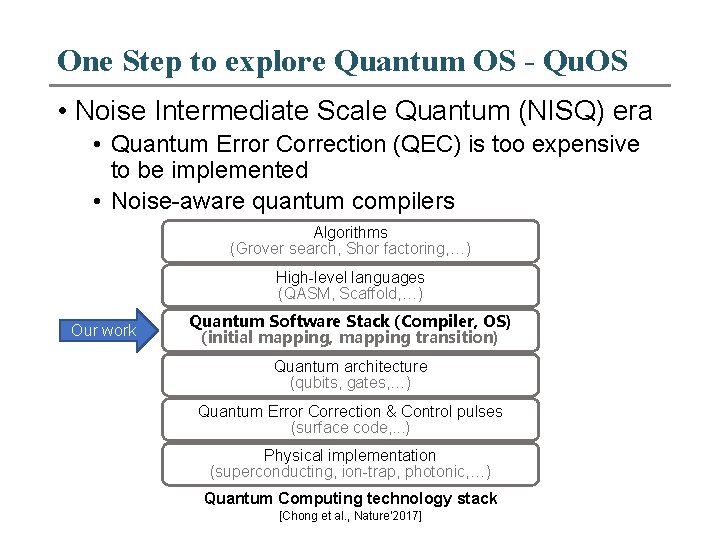
One Step to explore Quantum OS - Qu. OS • Noise Intermediate Scale Quantum (NISQ) era • Quantum Error Correction (QEC) is too expensive to be implemented • Noise-aware quantum compilers Algorithms (Grover search, Shor factoring, …) High-level languages (QASM, Scaffold, …) Our work Quantum Software Stack (Compiler, OS) (initial mapping, mapping transition) Quantum architecture (qubits, gates, …) Quantum Error Correction & Control pulses (surface code, . . . ) Physical implementation (superconducting, ion-trap, photonic, …) Quantum Computing technology stack [Chong et al. , Nature’ 2017]

Qubit Mapping Problem • Compilation workflow • Initial mapping generation: Map each logical qubit onto a physical qubit Q 0 Q 1 Q 2 Q 3 q 1 Q 4 q 2 Q 5 Q 6 Q 14 Q 13 Q 12 Q 11 q 3 Q 10 Q 9 Q 8 IBMQ 16 Q 7 q 1 q 2 q 3 H . . . T† Quantum program

Qubit Mapping Problem • Compilation workflow • Initial mapping generation: Map each logical qubit onto a physical qubit • Mapping transition: Making all gates executable by inserting CNOT q 1 q 3 can not be SWAPs executed directly Q 0 Q 1 Q 2 Q 3 q 1 Q 4 q 2 Q 5 Q 6 Q 14 Q 13 Q 12 Q 11 q 3 Q 10 Q 9 Q 8 IBMQ 16 Q 7 q 1 q 2 q 3 H . . . T† Quantum program

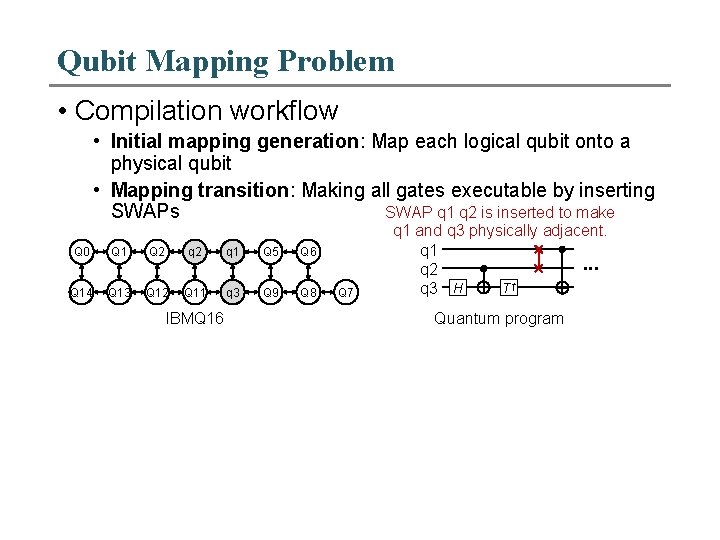
Qubit Mapping Problem • Compilation workflow • Initial mapping generation: Map each logical qubit onto a physical qubit • Mapping transition: Making all gates executable by inserting SWAP q 1 q 2 is inserted to make SWAPs Q 0 Q 1 Q 2 Q 3 q 2 Q 4 q 1 Q 5 Q 6 Q 14 Q 13 Q 12 Q 11 q 3 Q 10 Q 9 Q 8 IBMQ 16 Q 7 q 1 and q 3 physically adjacent. q 1. . . q 2 T† q 3 H Quantum program

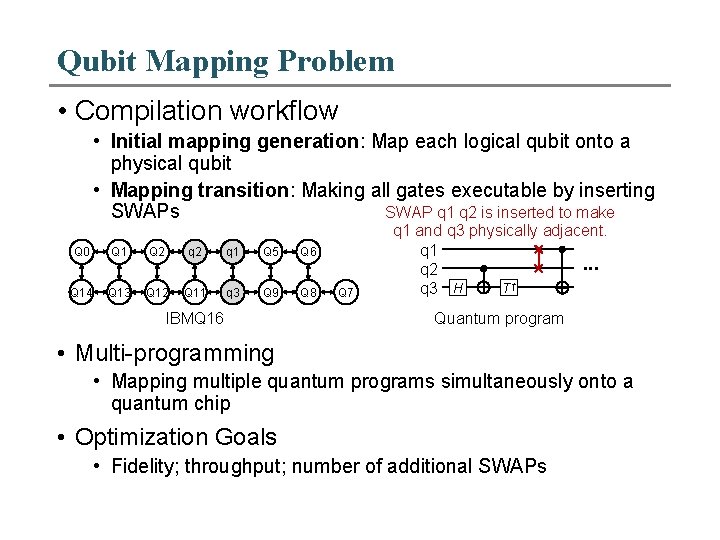
Qubit Mapping Problem • Compilation workflow • Initial mapping generation: Map each logical qubit onto a physical qubit • Mapping transition: Making all gates executable by inserting SWAP q 1 q 2 is inserted to make SWAPs Q 0 Q 1 Q 2 Q 3 q 2 Q 4 q 1 Q 5 Q 6 Q 14 Q 13 Q 12 Q 11 q 3 Q 10 Q 9 Q 8 IBMQ 16 Q 7 q 1 and q 3 physically adjacent. q 1. . . q 2 T† q 3 H Quantum program • Multi-programming • Mapping multiple quantum programs simultaneously onto a quantum chip • Optimization Goals • Fidelity; throughput; number of additional SWAPs

Outline q. Introduction q. Motivation q. Designs q. Evaluation q. Conclusion

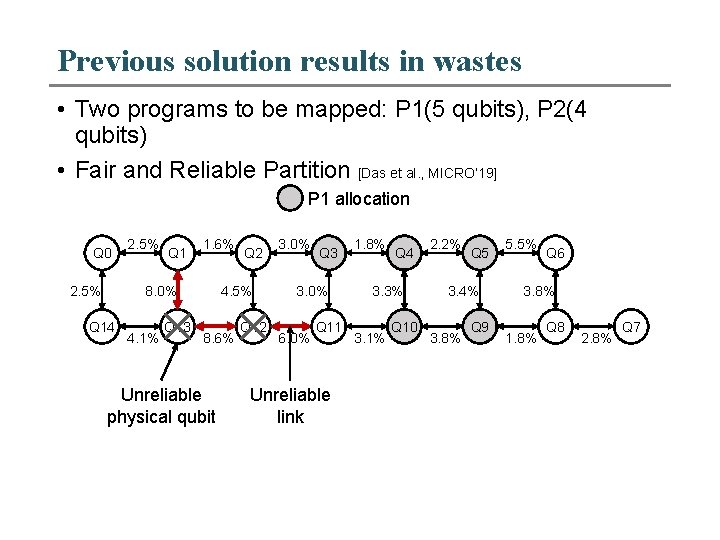
Previous solution results in wastes • Two programs to be mapped: P 1(5 qubits), P 2(4 qubits) • Fair and Reliable Partition [Das et al. , MICRO’ 19] P 1 allocation Q 0 2. 5% Q 1 1. 6% 8. 0% Q 14 4. 1% Q 13 Q 2 4. 5% 8. 6% Unreliable physical qubit Q 12 3. 0% Q 3 3. 0% 6. 0% Q 11 Unreliable link 1. 8% Q 4 3. 3% 3. 1% Q 10 2. 2% Q 5 3. 4% 3. 8% Q 9 5. 5% Q 6 3. 8% 1. 8% Q 8 2. 8% Q 7

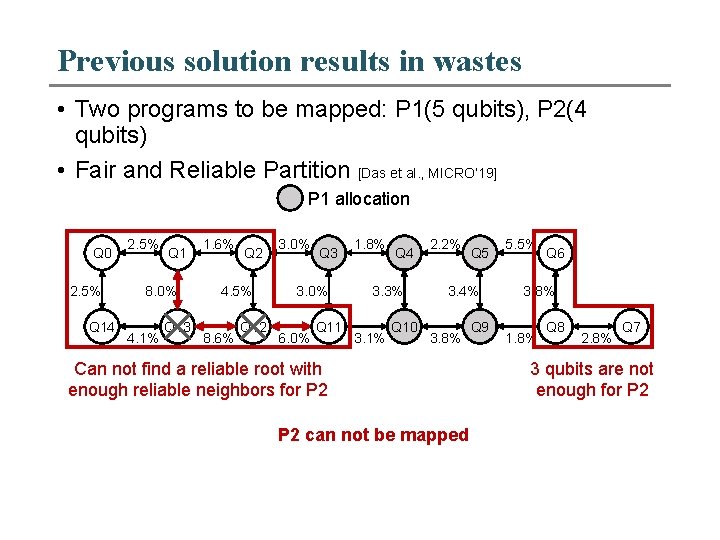
Previous solution results in wastes • Two programs to be mapped: P 1(5 qubits), P 2(4 qubits) • Fair and Reliable Partition [Das et al. , MICRO’ 19] P 1 allocation Q 0 2. 5% Q 14 2. 5% Q 1 8. 0% 4. 1% Q 13 1. 6% Q 2 4. 5% 8. 6% Q 12 3. 0% Q 3 3. 0% 6. 0% Q 11 1. 8% Q 4 3. 3% 3. 1% Q 10 2. 2% Q 5 3. 4% 3. 8% Can not find a reliable root with enough reliable neighbors for P 2 can not be mapped Q 9 5. 5% Q 6 3. 8% 1. 8% Q 8 2. 8% Q 7 3 qubits are not enough for P 2

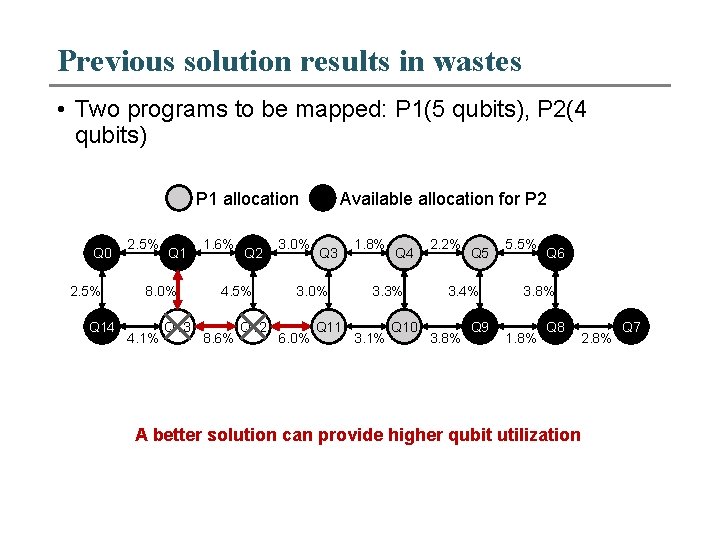
Previous solution results in wastes • Two programs to be mapped: P 1(5 qubits), P 2(4 qubits) P 1 allocation Q 0 2. 5% Q 14 2. 5% Q 1 8. 0% 4. 1% Q 13 1. 6% Q 2 4. 5% 8. 6% Q 12 3. 0% Available allocation for P 2 Q 3 3. 0% 6. 0% Q 11 1. 8% Q 4 3. 3% 3. 1% Q 10 2. 2% Q 5 3. 4% 3. 8% Q 9 5. 5% Q 6 3. 8% 1. 8% Q 8 2. 8% A better solution can provide higher qubit utilization Q 7

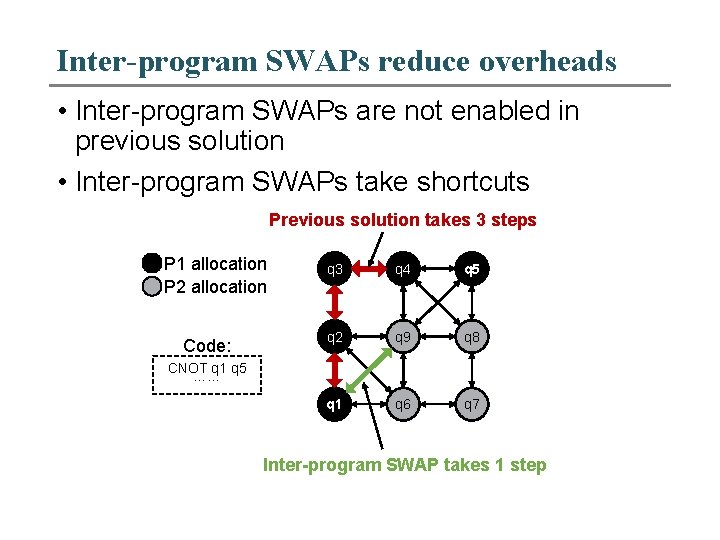
Inter-program SWAPs reduce overheads • Inter-program SWAPs are not enabled in previous solution • Inter-program SWAPs take shortcuts Previous solution takes 3 steps P 1 allocation P 2 allocation Code: q 3 q 4 q 5 q 2 q 9 q 8 q 1 q 6 q 7 CNOT q 1 q 5 …… Inter-program SWAP takes 1 step

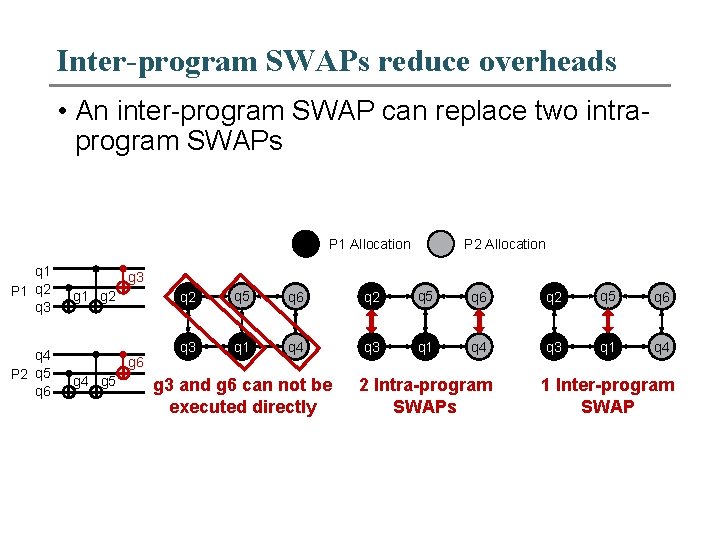
Inter-program SWAPs reduce overheads • An inter-program SWAP can replace two intraprogram SWAPs P 1 Allocation q 1 P 1 q 2 q 3 q 4 P 2 q 5 q 6 P 2 Allocation g 3 g 1 g 2 g 6 g 4 g 5 q 2 q 5 q 6 q 3 q 1 q 4 g 3 and g 6 can not be executed directly 2 Intra-program SWAPs 1 Inter-program SWAP

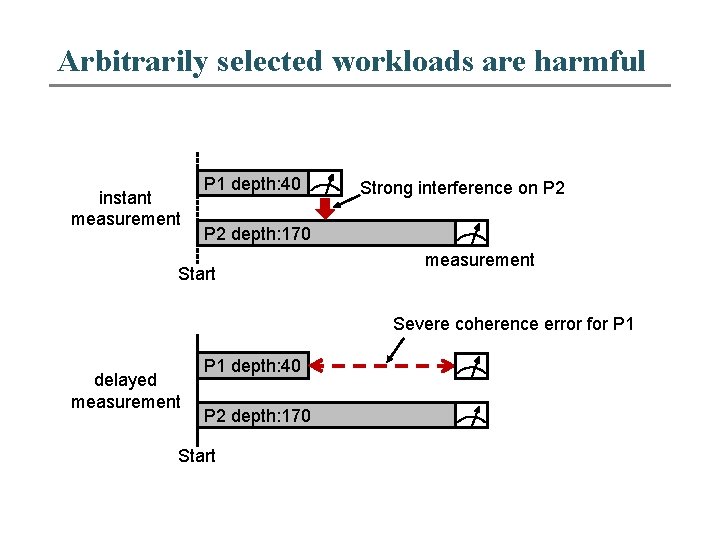
Arbitrarily selected workloads are harmful instant measurement P 1 depth: 40 Strong interference on P 2 depth: 170 Start measurement Severe coherence error for P 1 delayed measurement P 1 depth: 40 P 2 depth: 170 Start

Outline q. Introduction q. Motivation q. Designs q. Community Detection Assisted Partition q. X-SWAP Scheme q. Compilation Task Scheduler q. Evaluation q. Conclusion

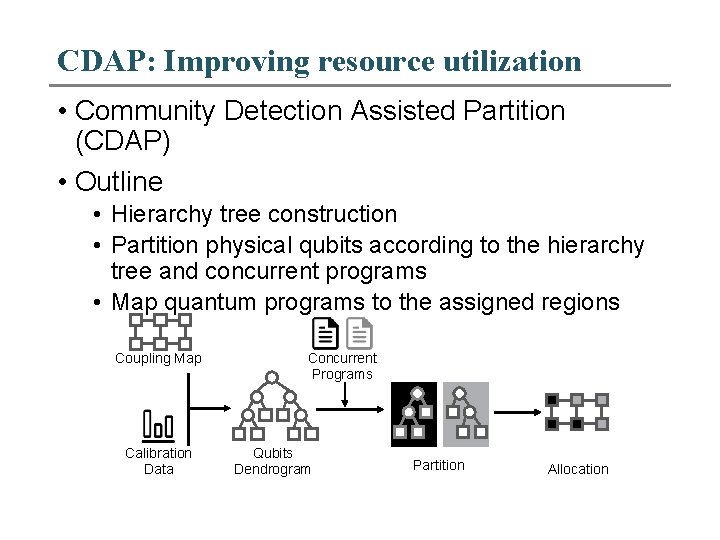
CDAP: Improving resource utilization • Community Detection Assisted Partition (CDAP) • Outline • Hierarchy tree construction • Partition physical qubits according to the hierarchy tree and concurrent programs • Map quantum programs to the assigned regions Coupling Map Calibration Data Concurrent Programs Qubits Dendrogram Partition Allocation

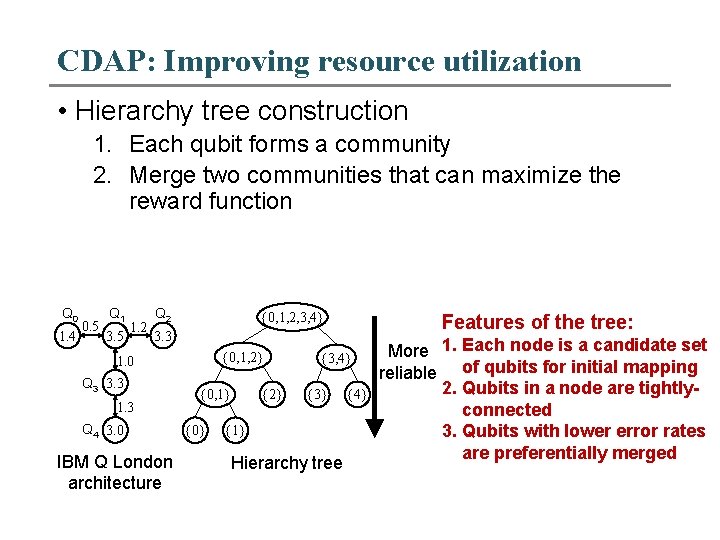
CDAP: Improving resource utilization • Hierarchy tree construction 1. Each qubit forms a community 2. Merge two communities that can maximize the reward function Q 0 1. 4 0. 5 Q 1 3. 5 1. 2 Q 2 {0, 1, 2, 3, 4} Features of the tree: 3. 3 {0, 1, 2} 1. 0 Q 3 3. 3 1. 3 Q 4 3. 0 IBM Q London architecture {0, 1} {0} {2} {3, 4} {3} {1} Hierarchy tree {4} More 1. Each node is a candidate set reliable of qubits for initial mapping 2. Qubits in a node are tightlyconnected 3. Qubits with lower error rates are preferentially merged

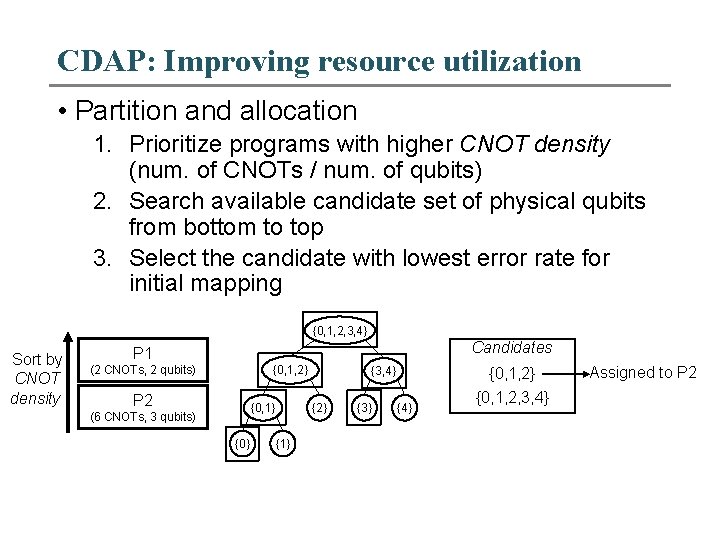
CDAP: Improving resource utilization • Partition and allocation 1. Prioritize programs with higher CNOT density (num. of CNOTs / num. of qubits) 2. Search available candidate set of physical qubits from bottom to top 3. Select the candidate with lowest error rate for initial mapping {0, 1, 2, 3, 4} Sort by CNOT density Candidates P 1 {0, 1, 2} (2 CNOTs, 2 qubits) P 2 {0, 1} (6 CNOTs, 3 qubits) {0} {3, 4} {2} {1} {3} {4} {0, 1, 2, 3, 4} Assigned to P 2

CDAP: Improving resource utilization • Partition and allocation 1. Prioritize programs with higher CNOT density (num. of CNOTs / num. of qubits) 2. Search available candidate set of physical qubits from bottom to top 3. Select the candidate with lowest error rate for initial mapping {3, 4} Sort by CNOT density Candidates {3, 4} P 1 (2 CNOTs, 2 qubits) {3} {3, 4} Assigned to P 1 {4} Allocate qubits to selected region with Greatest Weighted Edge First strategy [Murali et al. , ASPLOS’ 19]

Outline q. Introduction q. Motivation q. Designs q. Community Detection Assisted Partition q. X-SWAP Scheme q. Compilation Task Scheduler q. Evaluation q. Conclusion

X-SWAP: Reducing compilation overheads • Mapping transition: Insert SWAPs to make all 2 -qubit gates executable • Single-qubit gates are not considered during mapping transition • SWAP based heuristic search [Li et al. , ASPLOS’ 19] q 1 q 2 q 3 q 4 q 5 g 1 g 3 g 4 g 5 Front Layer g 2 l 1(F) l 2 l 3 Quantum Circuit g 1 g 2 g 3 g 4 g 5 l 4 Directed Acyclic Graph (DAG)

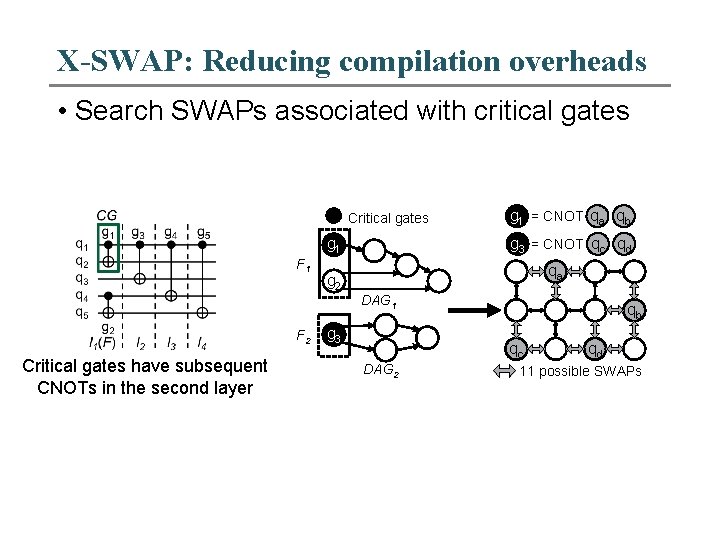
X-SWAP: Reducing compilation overheads • Search SWAPs associated with critical gates Critical gates g 3 = CNOT qc qd g 1 F 1 g 1 = CNOT qa qb qa g 2 DAG 1 F 2 Critical gates have subsequent CNOTs in the second layer g 3 qb qc DAG 2 qd 11 possible SWAPs

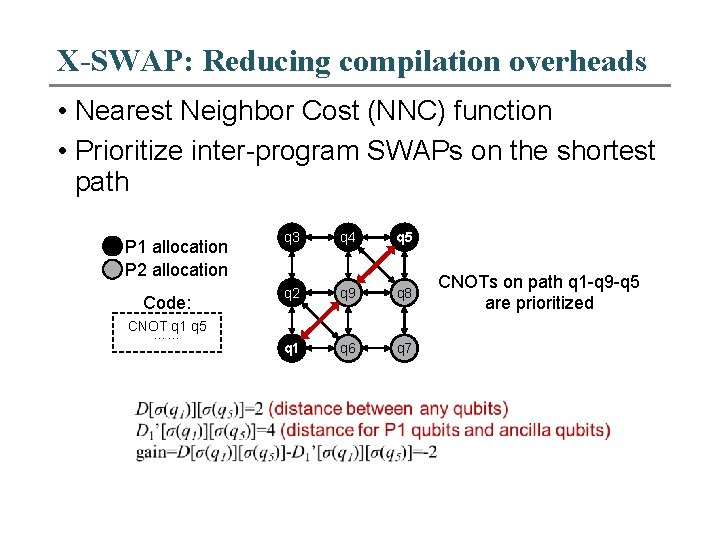
X-SWAP: Reducing compilation overheads • Nearest Neighbor Cost (NNC) function • Prioritize inter-program SWAPs on the shortest path P 1 allocation P 2 allocation Code: CNOT q 1 q 5 …… q 3 q 4 q 5 q 2 q 9 q 8 q 1 q 6 q 7 CNOTs on path q 1 -q 9 -q 5 are prioritized

Outline q. Introduction q. Motivation q. Designs q. Community Detection Assisted Partition q. X-SWAP Scheme q. Compilation Task Scheduler q. Evaluation q. Conclusion

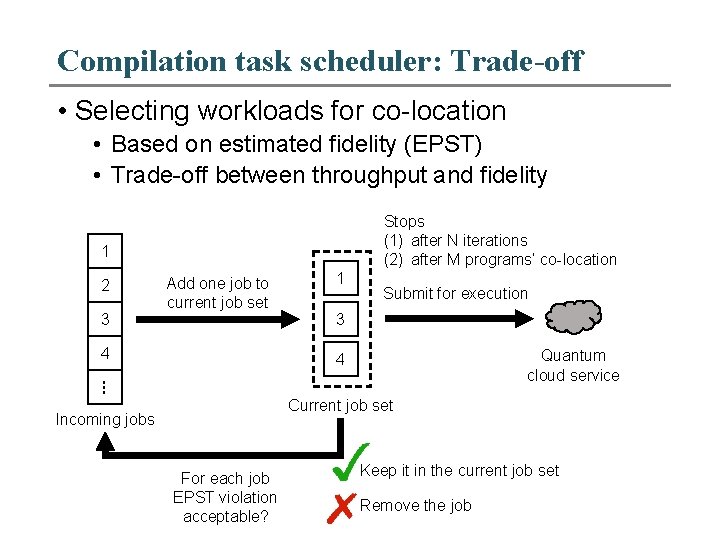
Compilation task scheduler: Trade-off • Selecting workloads for co-location • Based on estimated fidelity (EPST) • Trade-off between throughput and fidelity Stops (1) after N iterations (2) after M programs’ co-location 1 2 3 Add one job to current job set 4 1 Submit for execution 2 3 Quantum cloud service 4 … Current job set Incoming jobs For each job EPST violation acceptable? Keep it in the current job set Remove the job

Outline q. Introduction q. Motivation q. Designs q. Evaluation q. Conclusion

Metrics • Probability of a Successful Trial (PST): the fraction of trails that produce a correct result • Post-compilation gates number: especially CNOT gates • Trial Reduction Factor (TRF): the ratio of trails needed when programs are executed separately to the trails when multi-programming is enabled.

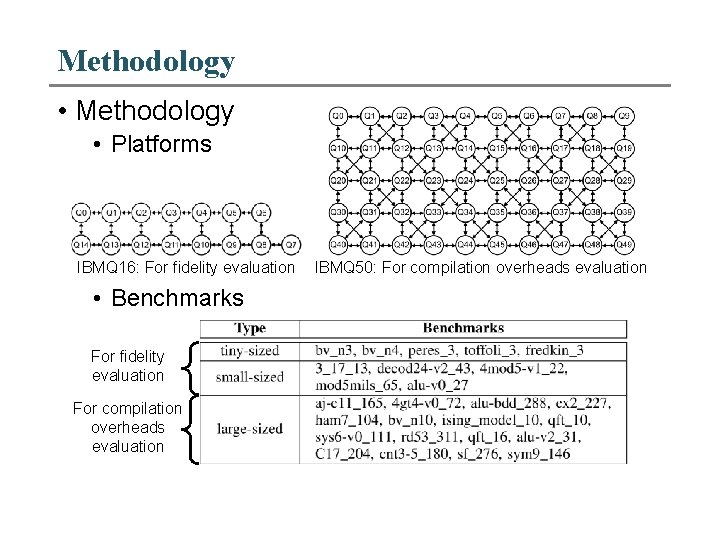
Methodology • Platforms IBMQ 16: For fidelity evaluation • Benchmarks For fidelity evaluation For compilation overheads evaluation IBMQ 50: For compilation overheads evaluation

Baseline • Separate execution • Multi-programming baseline [Das et al. , MICRO’ 19] • SABRE [Li et al. , ASPLOS’ 19] • Breakdown of our approach: • CDAP-only • X-SWAP-only • CDAP + X-SWAP

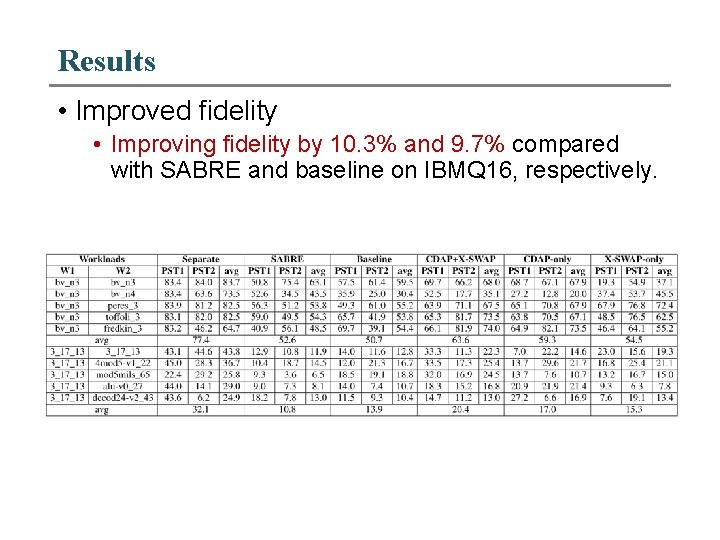
Results • Improved fidelity • Improving fidelity by 10. 3% and 9. 7% compared with SABRE and baseline on IBMQ 16, respectively.

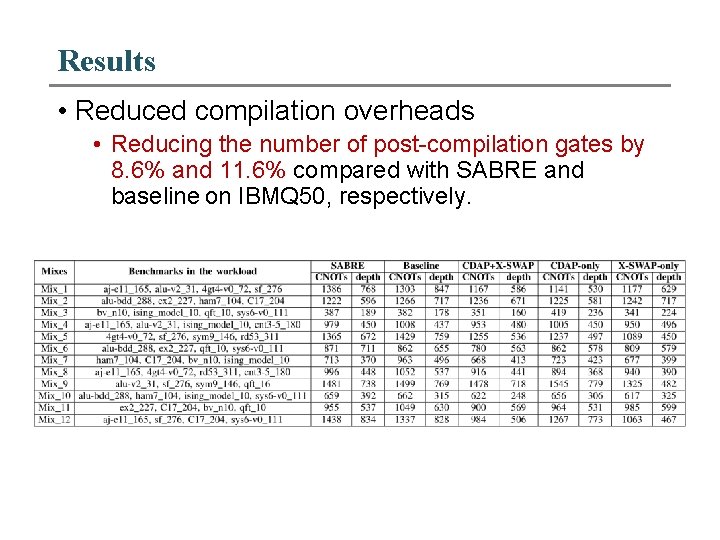
Results • Reduced compilation overheads • Reducing the number of post-compilation gates by 8. 6% and 11. 6% compared with SABRE and baseline on IBMQ 50, respectively.

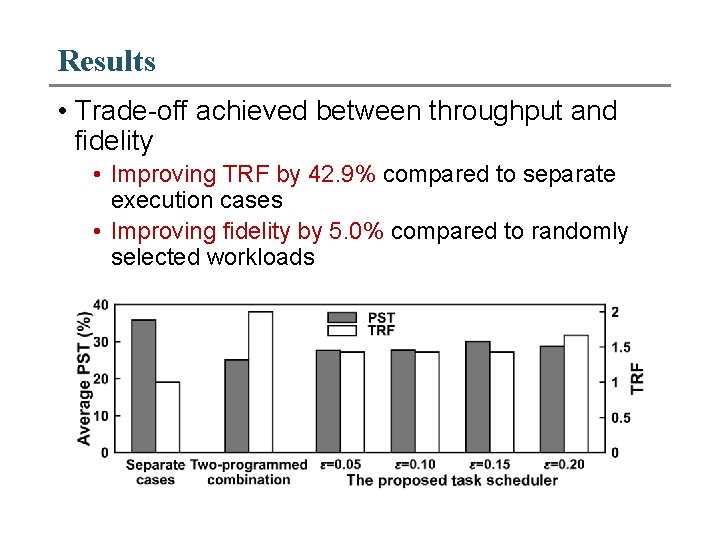
Results • Trade-off achieved between throughput and fidelity • Improving TRF by 42. 9% compared to separate execution cases • Improving fidelity by 5. 0% compared to randomly selected workloads

Outline q. Introduction q. Motivation q. Designs q. Evaluation q. Conclusion

Conclusion • Our work tackles the qubit mapping problem for multi-programing quantum computing • Our approach includes: 1. CDAP higher resource utilization, higher fidelity 2. X-SWAP less overheads 3. Compilation task scheduler fairness, tradeoff between throughput and fidelity

Thank You Lei Liu, Xinglei Dou Sys-Inventor Lab, SKLCA, ICT, CAS This presentation and recording belong to the authors. No distribution is allowed without the authors' permission.