QEC 07 General EntanglementAssisted Quantum ErrorCorrecting Codes Todd

QEC 07 General Entanglement-Assisted Quantum Error-Correcting Codes Todd A. Brun, Igor Devetak and Min-Hsiu Hsieh Communication Sciences Institute

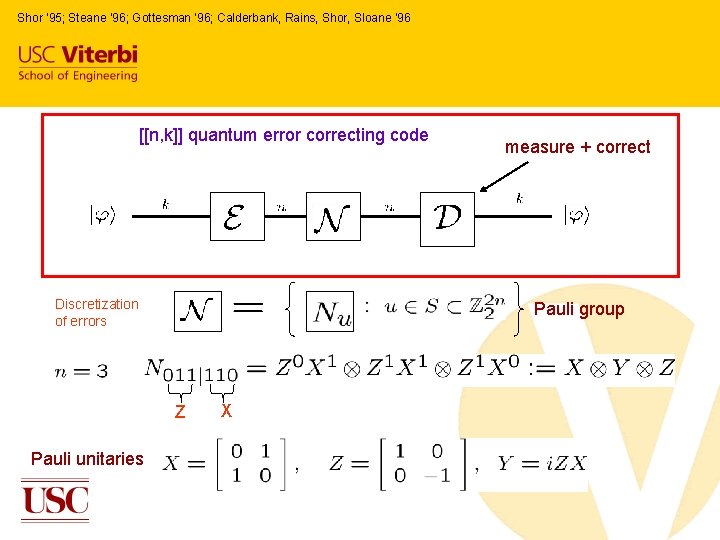
Shor ’ 95; Steane ‘ 96; Gottesman ’ 96; Calderbank, Rains, Shor, Sloane ‘ 96 [[n, k]] quantum error correcting code Discretization of errors Pauli group Z Pauli unitaries measure + correct X

Classical symplectic codes • The symplectic product • and is defined by commute (anti-commute) iff and commute • An [[n, k]] quantum error correcting code is described by a (n-k) £ 2 n parity check matrix H. Its rowspace B(H) is an isotropic subspace of n=5, k=1 commuting stabilizer generators dual containing code

Quantum stabilizer codes • The code space is defined as the simultaneous +1 eigenspace of the stabilizer operators • The correctable error set E is defined by: If E 1 and E 2 are in E, then at least one of the two conditions hold: distinct error syndromes degenerate code Y error on 4 th q-bit • Correction involves measuring the “error syndrome” (i. e. the simultaneous eigenvector of the stabilizer generators) ,

Properties of Stabilizer Codes We can see that stabilizer codes have the following properties: 1. The code corresponds to an isotropic (that is, dualcontaining) classical code over a symplectic space. 2. The error correcting conditions are almost the same as classical (except for the existence of degenerate quantum codes, in which distinct errors share the same error syndrome). 3. Correction consists of measuring an error syndrome and performing an appropriate correcting action (a unitary).

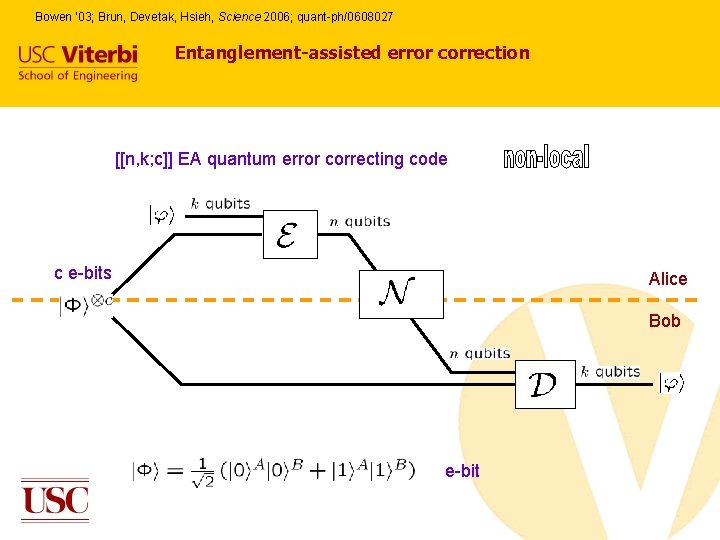
Bowen ‘ 03; Brun, Devetak, Hsieh, Science 2006; quant-ph/0608027 Entanglement-assisted error correction [[n, k; c]] EA quantum error correcting code c e-bits Alice Bob e-bit

Entanglement-assisted stabilizer formalism It turns out that we can establish a simple extension of the usual stabilizer formalism to describe entanglement-assisted codes. We again establish a “stabilizer” which is a subgroup of the Pauli group on n q-bits; but we no longer require this subgroup to be Abelian. For such a subgroup, we can find a set of generators which fall into two groups: Isotropic generators, which commute with all other generators; and Symplectic generators, which come in anticommuting pairs; each pair commutes with all other generators.

Entanglement-assisted stabilizer formalism • An [[n, k; c]] EA quantum error correcting code is described by a (n-k) £ 2 n parity check matrix H. B = rowspace(H). Again, • Take a general symplectic matrix H. Its rowspace B can be written as symplectic pairs • Canonical example The isotropic generators generate SI and the symplectic generators generate SE.

n = 3, k = 1, c = 2 [[3, 1; 2]] code stabilized by Measure in the simultaneous eigenbasis of

• The correctable error set E is defined by: If E 1 and E 2 are in E, then at least one of the two conditions hold: degenerate code • The code space is defined as the simultaneous +1 eigenspace of the stabilizer generators n c n • Decoding involves measuring the “error syndrome” (i. e. the simultaneous eigenvector of the stabilizer generators) , c

Properties of the entanglement-assisted stabilizer formalism We can now compare the properties of an EAQECC to those of an ordinary QECC: 1. The code corresponds to a classical code over a symplectic space. (No longer needs to be dual-containing!) 2. The error correcting conditions are almost the same as classical (except for the existence of degenerate quantum codes, in which distinct errors share the same error syndrome). 3. Correction consists of measuring an error syndrome and performing an appropriate correcting action (a unitary).

The GF(4) Construction • Natural isometry between GF(4) and (Z 2)2 • Any dual containing classical [n, k, d]4 code can be made into a [[n, 2 k–n, d]] QECC • Now: Any classical [n, k, d]4 code can be made into a [[n, 2 k-n+c, d; c]] catalytic QECC for some c • When the classical code attains the Singleton bound n-k ¸ d-1 the quantum code attains the quantum Singleton bound n-k ¸ 2(d-1) • When the classical code attains the Shannon limit 2 – H 4(1 – 3 p, p, p, p) on a quaternary symmetric channel, the quantum code attains the Hashing limit 1 -H 2(1 -3 p, p, p, p). • Modern classical codes (LDPC, turbo) can now be made quantum without having to be dual-containing.

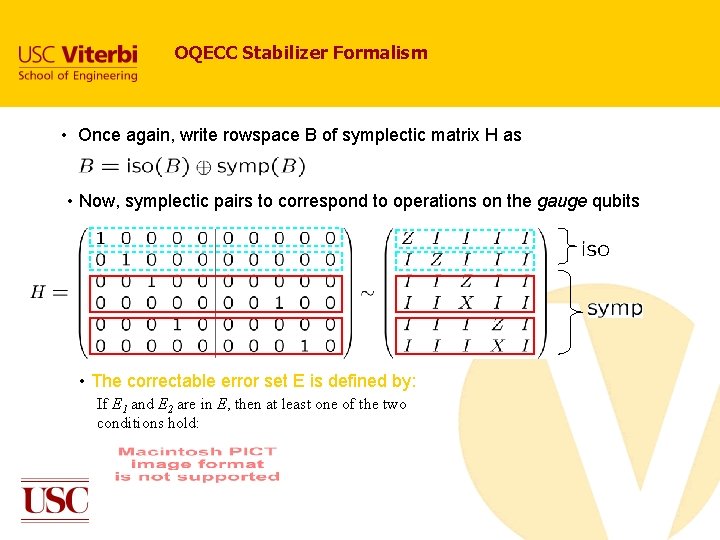
Poulin; Bacon; Aly, Klappenecker and Sarvepalli Operator QECCs The basic idea of operator QECCs is that part of the system (the noisy or gauge part) contains no information about either the quantum information to be transmitted or the errors which occur. We allow arbitrary noise to affect this gauge subsystem. An [[n, k; r]] OQECC: r = number of gauge q-bits Because the gauge subsystem can be in any arbitrary state, OQECCs are not subspaces. (That is, the superposition of two valid states in the OQECC is not a valid state unless they have the same state for the gauge subsystem. )

OQECC Stabilizer Formalism • Once again, write rowspace B of symplectic matrix H as • Now, symplectic pairs to correspond to operations on the gauge qubits • The correctable error set E is defined by: If E 1 and E 2 are in E, then at least one of the two conditions hold:

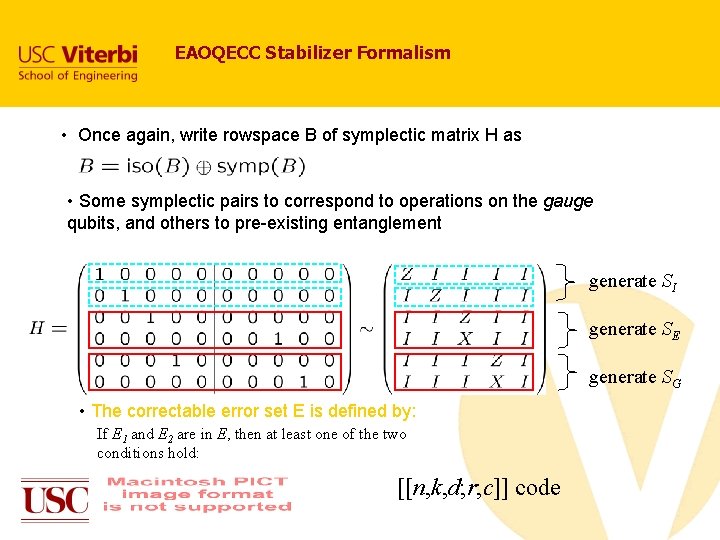
Hsieh, Devetak, Brun, ISIT June 2007; quant-ph/0708. 2142 (to appear PRA); Gilbert et al. quant-ph/0709. 0128 Entanglement-assisted operator quantum errorcorrecting codes Both EAQECCs and OQECCs extend the stabilizer formalism by allowing a noncommuting “stabilizer” group. EAQECCs add an extra e-bit for each symplectic pair in the set of generators. OQECCs drop these noncommuting pairs of generators, and identify states which differ by the action of gauge operators. One can combine these approaches: use entanglement to retain some of the symplectic group in the stabilizer, while gauging out the rest. The same classical symplectic code can thus produce a range of quantum codes, combining different degrees of entanglement-assistance and passive correction. This is the most general extension of stabilizer codes so far constructed.

EAOQECC Stabilizer Formalism • Once again, write rowspace B of symplectic matrix H as • Some symplectic pairs to correspond to operations on the gauge qubits, and others to pre-existing entanglement generate SI generate SE generate SG • The correctable error set E is defined by: If E 1 and E 2 are in E, then at least one of the two conditions hold: [[n, k, d; r; c]] code

Examples The [8, 1, 3; 1] EAQECC can be made an [8, 1, 3; 2; 1] EAOQECC by dropping two generators from SI and adding them and their symplectic partners to SG. (This example is based on the 9 -bit Shor code. )

We can construct another example from classical BCH codes. Replacing by its binary representation produces a [63, 39, 9] classical BCH code, which gives a [[63, 21, 9; 6]] EAQECC. Making some symplectic pairs into gauge operators yields: n k d r c 63 21 9 0 6 63 21 7 1 5 63 21 7 2 4 63 21 7 3 3 63 21 7 4 2 63 21 7 5 1 63 21 7 6 0

Conclusions • Almost all known quantum error-correcting codes are stabilizer codes. These have a connection to classical symplectic codes, but only for dualcontaining codes. • Two extensions beyond this scheme which do not require this constraint are entanglement-assisted QECCs and operator QECCs. Both yield noncommuting “stabilizers” which are dealt with in different ways. • These two extensions can usefully be combined into general EAOQECCs, which gives considerable flexibility in constructing QECCs from classical codes. • Welcome to Sunny Southern California!