QCD Critical Point and Its Effects on Physical

QCD Critical Point and Its Effects on Physical Observables Schematic Consideration Masayuki ASAKAWA Department of Physics, Osaka University in collaboration with C. Nonaka, B. Müller, S. A. Bass April 2008 @ Brookhaven National Laboratory

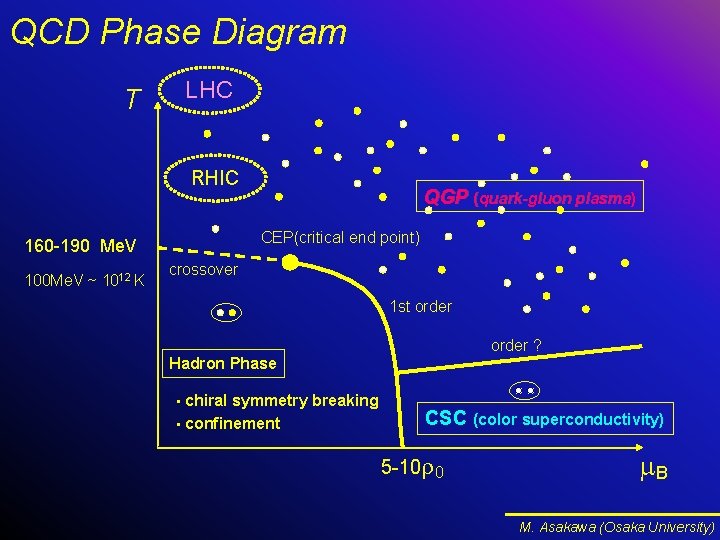
QCD Phase Diagram LHC T RHIC CEP(critical end point) 160 -190 Me. V 100 Me. V ~ 1012 K QGP (quark-gluon plasma) crossover 1 st order ? Hadron Phase chiral symmetry breaking • confinement • CSC (color superconductivity) 5 -10 r 0 B M. Asakawa (Osaka University)

20 th Anniversary of CEP in QCD M. Asakawa (Osaka University)

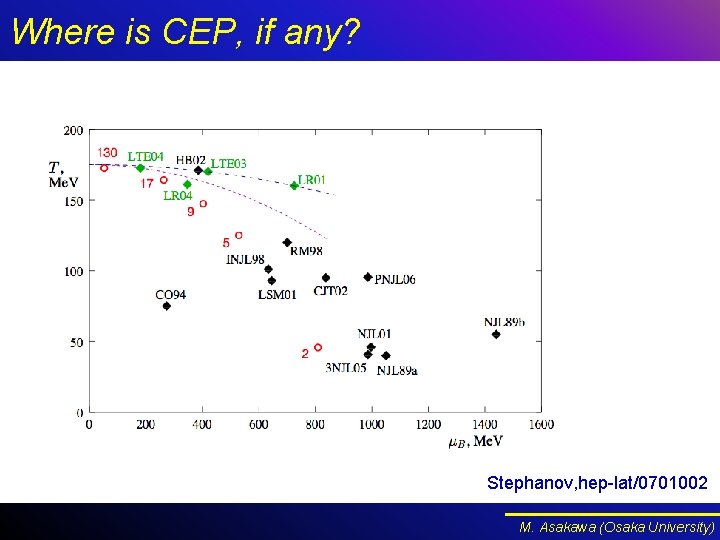
Where is CEP, if any? Stephanov, hep-lat/0701002 M. Asakawa (Osaka University)

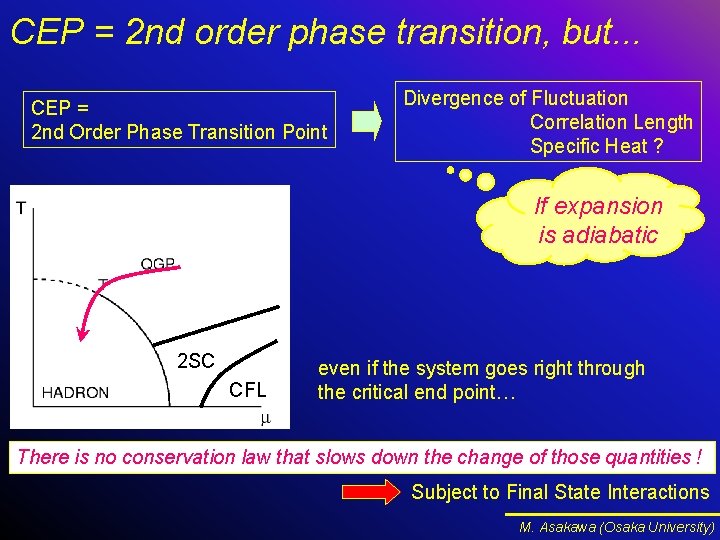
CEP = 2 nd order phase transition, but. . . CEP = 2 nd Order Phase Transition Point Divergence of Fluctuation Correlation Length Specific Heat ? If expansion is adiabatic 2 SC CFL even if the system goes right through the critical end point… There is no conservation law that slows down the change of those quantities ! Subject to Final State Interactions M. Asakawa (Osaka University)

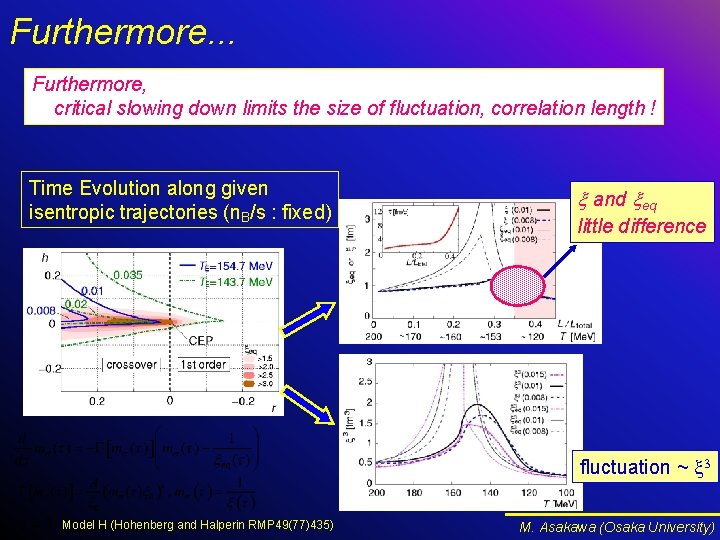
Furthermore. . . Furthermore, critical slowing down limits the size of fluctuation, correlation length ! Time Evolution along given isentropic trajectories (n. B/s : fixed) x and xeq little difference fluctuation ~ x 3 Model H (Hohenberg and Halperin RMP 49(77)435) M. Asakawa (Osaka University)

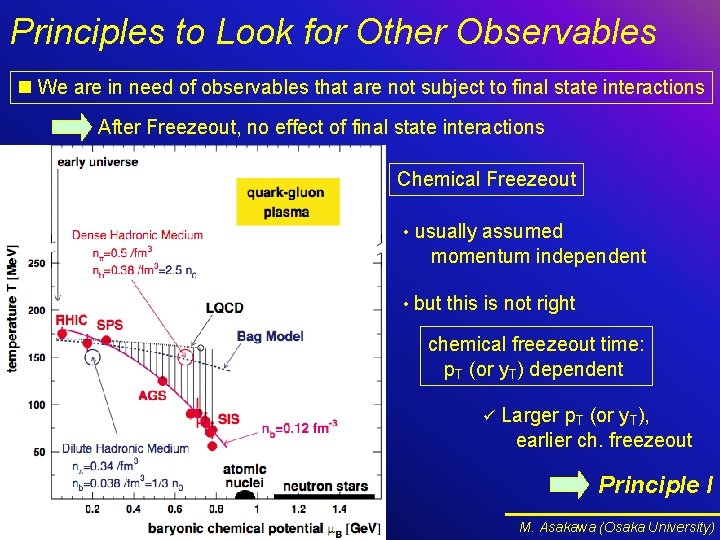
Principles to Look for Other Observables n We are in need of observables that are not subject to final state interactions After Freezeout, no effect of final state interactions Chemical Freezeout • usually assumed momentum independent • but this is not right chemical freezeout time: p. T (or y. T) dependent ü Larger p. T (or y. T), earlier ch. freezeout Principle I M. Asakawa (Osaka University)

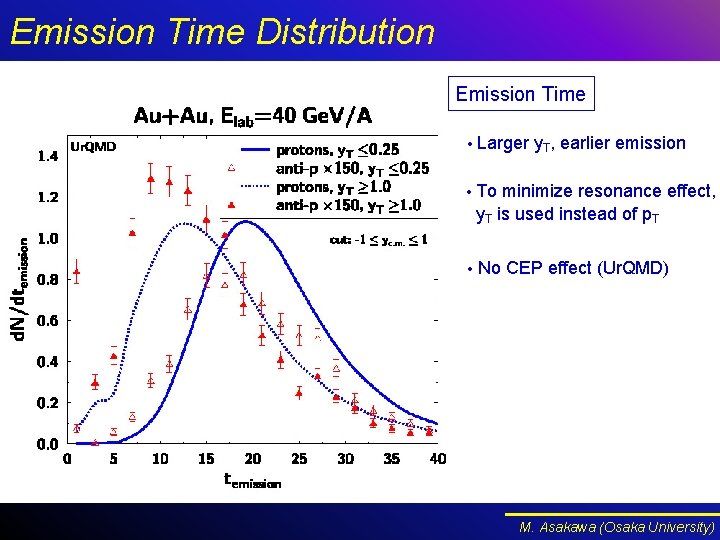
Emission Time Distribution Emission Time • Larger y. T, earlier emission • To minimize resonance effect, y. T is used instead of p. T • No CEP effect (Ur. QMD) M. Asakawa (Osaka University)

Principle II Universality: QCD CEP belongs to the same universality class as 3 d Ising Model Lattice QCD at finite density: still in its infancy For critical behavior: need to carry out V limit same universality class 3 d Ising Model End Point QCD Critical End Point (T, m. B) (r, h) h : external magnetic field M. Asakawa (Osaka University)

What is not universal n Further Assumptions • Size of Critical Region No general universality • Lattice calculation: not yet V limit • Renormalization group analysis in Effective Models ? • need to be treated as an input, at the moment • Mapping T h r is not an assumption M. Asakawa (Osaka University)

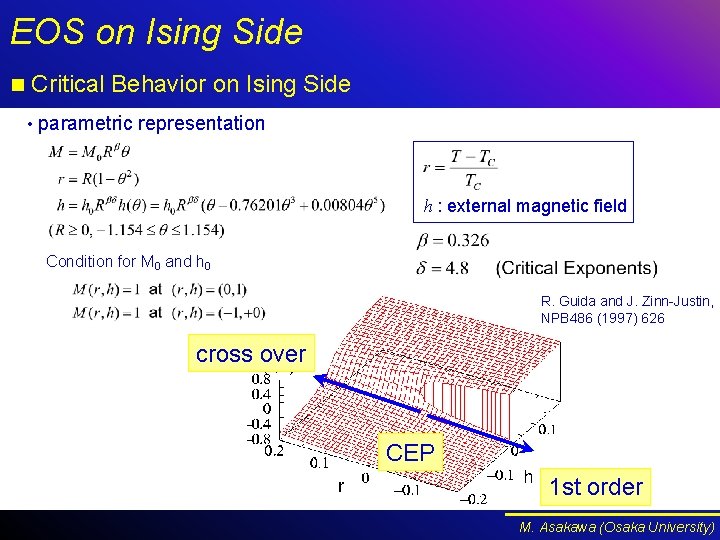
EOS on Ising Side n Critical Behavior on Ising Side • parametric representation h : external magnetic field Condition for M 0 and h 0 R. Guida and J. Zinn-Justin, NPB 486 (1997) 626 cross over CEP 1 st order M. Asakawa (Osaka University)

Singular Part + Non-singular Part n Matching between Hadronic and QGP EOS • Entropy Density consists of Singular and Non-Singular Parts n Requirement: • Only Singular Part shows universal behavior reproduce both the singular behavior and know asymptotic limits n Matched Entropy Density Hadron Phase (excluded volume model) QGP phase Bcrit • Dimensionless Quantity: Sc D: related to extent of critical region M. Asakawa (Osaka University)

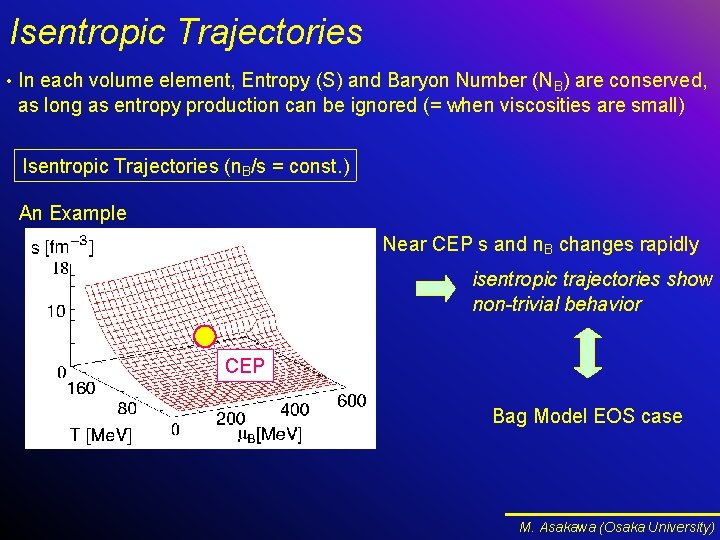
Isentropic Trajectories • In each volume element, Entropy (S) and Baryon Number (NB) are conserved, as long as entropy production can be ignored (= when viscosities are small) Isentropic Trajectories (n. B/s = const. ) An Example Near CEP s and n. B changes rapidly isentropic trajectories show non-trivial behavior CEP Bag Model EOS case M. Asakawa (Osaka University)

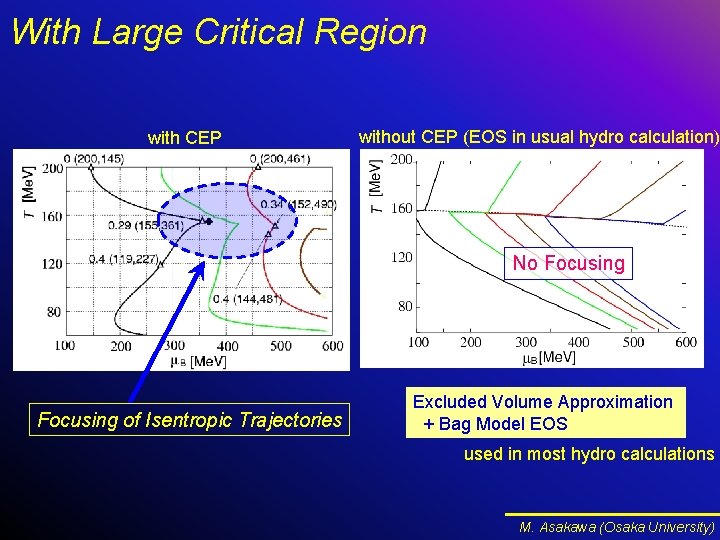
With Large Critical Region with CEP without CEP (EOS in usual hydro calculation) No Focusing of Isentropic Trajectories Excluded Volume Approximation + Bag Model EOS used in most hydro calculations M. Asakawa (Osaka University)

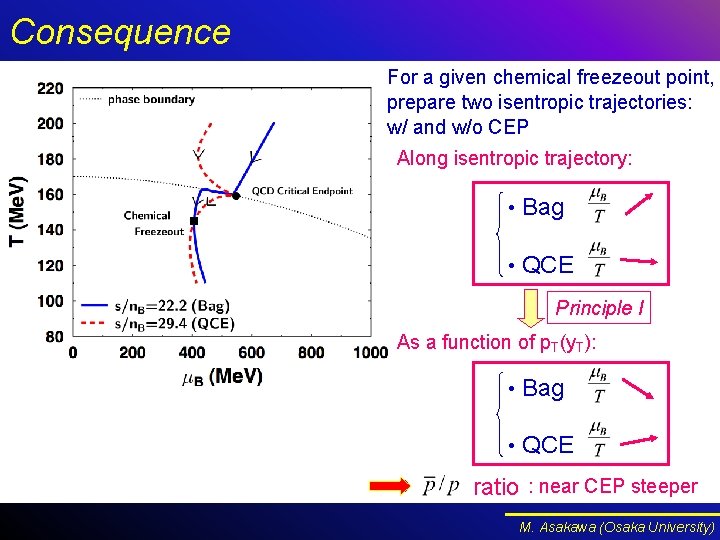
Consequence For a given chemical freezeout point, prepare two isentropic trajectories: w/ and w/o CEP Along isentropic trajectory: • Bag • QCE Principle I As a function of p. T(y. T): • Bag • QCE ratio : near CEP steeper M. Asakawa (Osaka University)

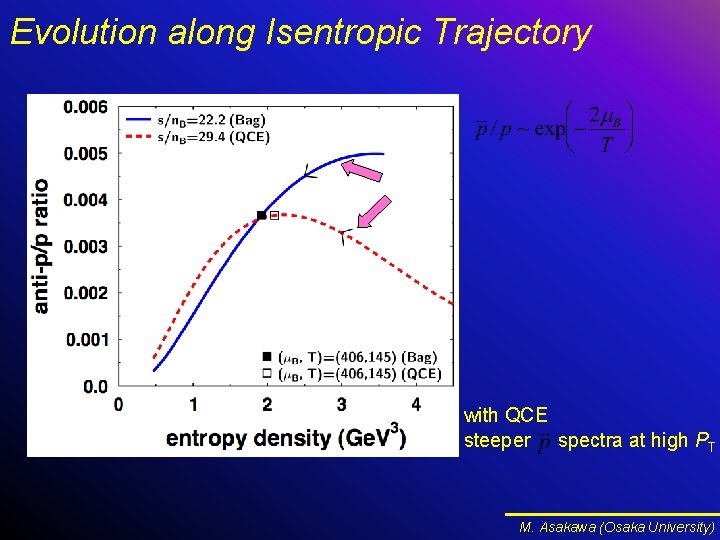
Evolution along Isentropic Trajectory with QCE steeper spectra at high PT M. Asakawa (Osaka University)

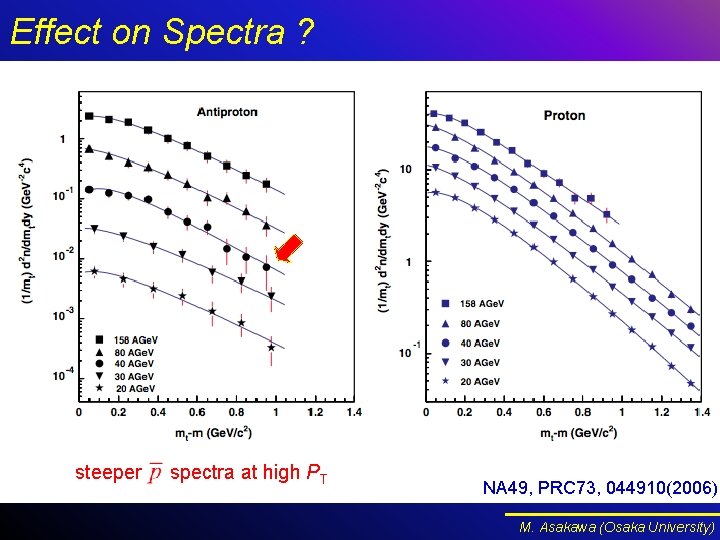
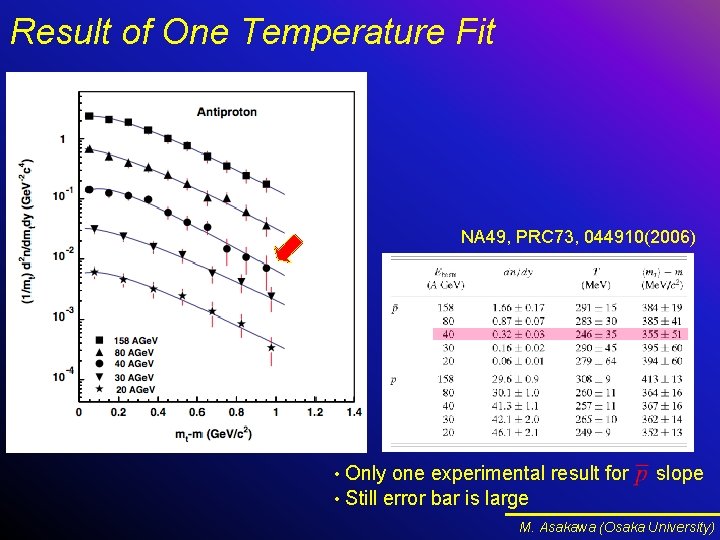
Effect on Spectra ? steeper spectra at high PT NA 49, PRC 73, 044910(2006) M. Asakawa (Osaka University)

Result of One Temperature Fit NA 49, PRC 73, 044910(2006) Only one experimental result for • Still error bar is large • slope M. Asakawa (Osaka University)

Summary n Two Principles: i) Chemical Freezeout is p. T(y. T) dependent ii) Isentropic Trajectory behaves non-trivially near CEP (focusing) ratio behaves non-monotonously near CEP Information on the QCD critical point: such as location, size of critical region, existence… n n We then made a data search • turned out NA 49 data shows non-trivial behavior around 40 Ge. V/A • still error bar is large, finer energy scans at SPS, FAIR, RHIC: desirable Effect on Flow ? cs changes differently from the case with EOS used in usual hydro cal. (3 D hydro cal. with CEP + Ur. QMD: C. Nonaka in progress) M. Asakawa (Osaka University)