q q q Pengertian Data Statistik Penyusunan dan

q q q Pengertian Data Statistik Penyusunan dan Penyajian Data Ukuran Pemusatan Ukuran Penyebaran

A. Pengertian Statistik dan statistika STATISTIKA adalah ilmu tentang cara-cara mengumpukan, mengolah, menganalisis, dan mencari keterangan yang berarti dari data yang berupa angka. Pengertian lain : pengetahuan yang berhubungan dengan pengumpulan data yang penyelidikan dan kesimpulannya berdasarkan bukti-bukti yang berupa catatan bilangan/ angka. Data-data berupa angka yang dikumpulkan, diolah, dianalisis itu disebut dengan STATISTIK Menurut tingkat pengerjaan yang dapat dilakukan, statistika dibagi menjadi dua yaitu : Statistika Deskriptif adalah teknik mengumpulkan, mengolah dan menganalisis data yang diperoleh dari populasi Statistika Inferensial (Induktif) adalah teknik mengumpulkan, mengolah dan menganalisis data dari sampel acak untuk mengambil kesimpulan tentang ciri-ciri populasi tertentu.

B. Data Statistik 1. Syarat-syarat data yang baik harus : a. Obyektif (sesuai dengan keadaan sebenarnya) b. Representatif /mewakili. Misal : data ttg harga 9 barang pokok harus diambil dari pasar rakyat, swalayan, dll c. Mempunyai kesalahan baku sangat kecil d. Tepat waktu : data tahun 2003 tidak diambil dari data tahun 2000 e. Relevan terhadap suatu masalah 2. Macam-macam data a. Sesuai bentuknya 1) Data Kuantitatif : data yang dinyatakan dalam bentuk bilangan a) Data Diskrit diperoleh dari hasil membilang Contoh : Jumlah bola, siswa satu kelas, botol 1 dus b) Data kontinu diperoleh dari hasil mengukur/menimbang Contoh : luas tanah, kecepatan mobil, berat badan, dll 2) Data Kualitatif : data yang tidak dapat dinyatakan dlm bilangan Contoh : agama, status, jenis kelamin, dll

b. Sesuai asalnya 1) Data Internal misal dari suatu perusahaan didapatkan data keuangan, personalia, produksi, dll 2) Data Eksternal diperoleh di luar. Misal : Data harga pasar, daya beli masyarakat, dll c. Berdasarkan cara memperolehnya : 1) Data Primer : diperoleh langsung dari obyeknya. 2) Data Sekunder : diperoleh dari pihak lain 3. Cara Mengumpulkan data a. Metode Sensus : Data seluruh obyek yang diteliti b. Metode Sampling : meneliti sebagian dari seluruh obyek Semuanya dapat dilakukan dengan dua cara : a. Wawancara / tanya jawab langsung b. Lembar pertanyaan / quesioner

C. Penyusunan dan Penyajian data Setelah data terkumpul, maka data tersebut disusun. Cara penyusunan ada dua cara : 1. Array adalah penyusunan data menurut besarnya, menaik/menurun Cara ini baik digunakan jika datanya sedikit. Contoh : Diperoleh data : 8 7 9 4 7 3 9 7 2 8 5 7 2 9 7 Jika data tersebut disusun secara Array menjadi : Urut naik : 2 2 3 4 5 7 7 7 8 8 9 9 9 Urut turun : 9 9 9 8 8 7 7 7 5 4 3 2 2

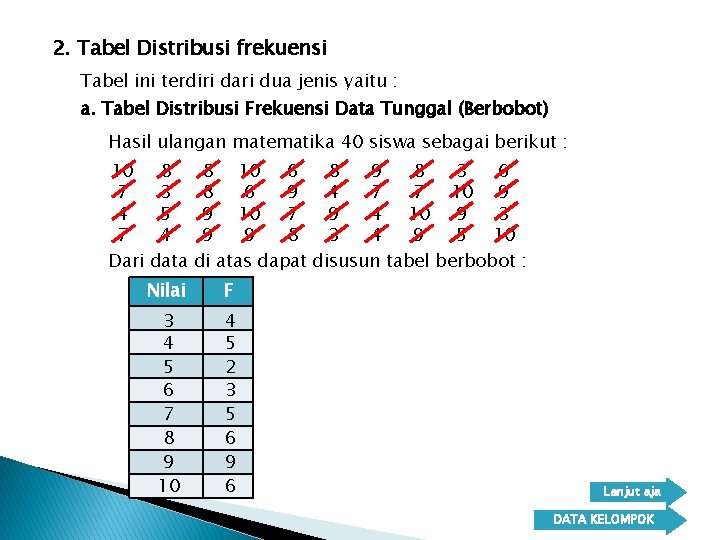
2. Tabel Distribusi frekuensi Tabel ini terdiri dari dua jenis yaitu : a. Tabel Distribusi Frekuensi Data Tunggal (Berbobot) Hasil ulangan matematika 40 siswa sebagai berikut : 10 7 4 7 Dari 8 3 5 4 data 8 10 6 8 9 8 3 6 8 6 9 4 7 7 10 9 9 10 7 9 4 10 9 3 9 9 8 3 4 9 5 10 di atas dapat disusun tabel berbobot : Nilai F 3 4 5 6 7 8 9 10 4 5 2 3 5 6 9 6 Lanjut aja DATA KELOMPOK

2. Tabel Distribusi frekuensi Tabel ini terdiri dari dua jenis yaitu : a. Tabel Distribusi Frekuensi Data Tunggal (Berbobot) Hasil ulangan matematika 40 siswa sebagai berikut : 10 7 4 7 Dari 8 3 5 4 data Nilai 3 4 5 6 7 8 9 10 8 10 6 8 9 8 3 6 8 6 9 4 7 7 10 9 9 10 7 9 4 10 9 3 9 9 8 3 4 9 5 10 di atas dapat disusun tabel berbobot : Turus/Tally F 4 5 2 3 5 6 9 6 n i a l a r a C Back Go

b. Tabel Distribusi Frekuensi Data Kelompok : Untuk mengelompokkan data ini melalui langkah-langkah menentukan: 1. Besarnya jangkauan (R) atau selisih nilai data maksimum dengan nilai data minimum 2. Banyaknya kelas dengan aturan struges yaitu : k = 1 + 3, 3 log n k = banyaknya kelas; n = banyaknya data 3. Panjang atau interval kelas (i) dengan rumus : i= Interval yang digunakan sedikit lebih besar daripada i. Misal jika i = 6, 4 maka digunakan i = 7 Jika i = 5 maka digunakan i = 6 4. Menyusun tabel dengan turus

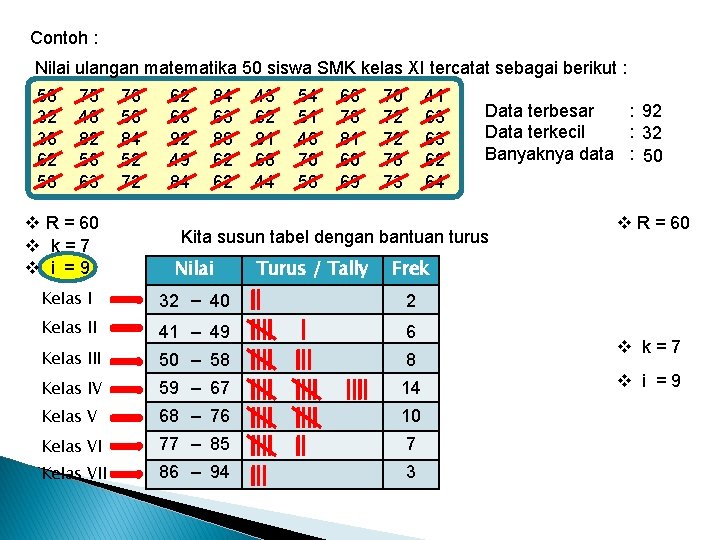
Contoh : Nilai ulangan matematika 50 siswa SMK kelas XI tercatat sebagai berikut : 58 32 36 62 58 75 48 82 56 63 76 56 84 52 72 62 66 92 49 84 84 63 88 62 62 43 62 91 68 44 54 51 46 70 58 66 78 81 60 69 70 72 72 78 73 41 63 63 62 64 Data terbesar : 92 Data terkecil : 32 Banyaknya data : 50 v Range (jangkauan) = 92 – 32 = 60 v R = 60 v Banyaknya kelas k = = = v k=7 v Interval kelas 1 + 3, 3 log n 1 + 3, 3 log 50 1 + 3, 3 (1, 699) 1 + 5, 6067 6, 6067 7 (dibulatkan ke atas) i = R = 60 = 8, 57 9 (dibulatkan ke atas) k 7 v i =9

Contoh : Nilai ulangan matematika 50 siswa SMK kelas XI tercatat sebagai berikut : 58 32 36 62 58 75 48 82 56 63 76 56 84 52 72 62 66 92 49 84 84 63 88 62 62 43 62 91 68 44 54 51 46 70 58 66 78 81 60 69 70 72 72 78 73 41 63 63 62 64 v R = 60 v k=7 v i =9 Nilai Kelas I 32 – 40 2 Kelas II 41 – 49 6 Kelas III 50 – 58 8 Kelas IV 59 – 67 14 Kelas V 68 – 76 10 Kelas VI 77 – 85 7 Kelas VII 86 – 94 3 Data terbesar : 92 Data terkecil : 32 Banyaknya data : 50 Kita susun tabel dengan bantuan turus Turus / Tally v R = 60 Frek v k=7 v i =9

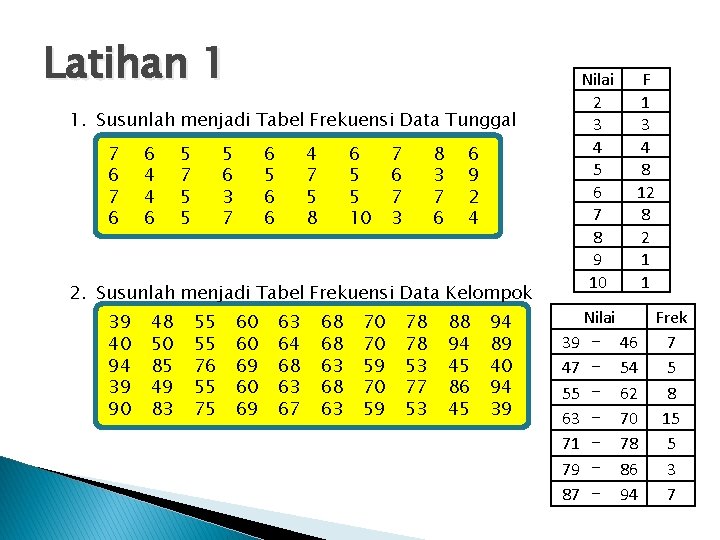
Latihan 1 1. Susunlah menjadi Tabel Frekuensi Data Tunggal 7 6 6 4 4 6 5 7 5 5 5 6 3 7 6 5 6 6 4 7 5 8 6 5 5 10 7 6 7 3 8 3 7 6 6 9 2 4 2. Susunlah menjadi Tabel Frekuensi Data Kelompok 39 40 94 39 90 48 50 85 49 83 55 55 76 55 75 60 60 69 63 64 68 63 67 68 68 63 70 70 59 78 78 53 77 53 88 94 45 86 45 94 89 40 94 39 Nilai 2 3 4 5 6 7 8 9 10 F 1 3 4 8 12 8 2 1 1 Nilai Frek 39 - 46 7 47 - 54 5 55 - 62 8 63 - 70 15 71 - 78 5 79 - 86 3 87 - 94 7

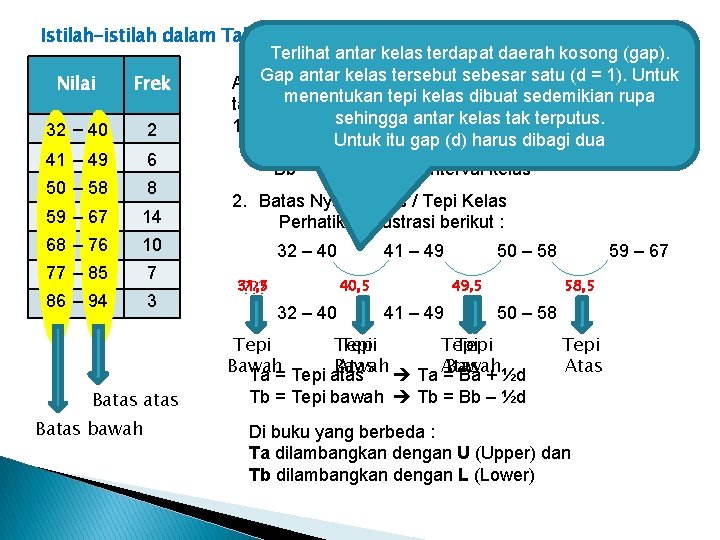
Istilah-istilah dalam Tabel frekuensi Data Kelompok Terlihat antar kelas terdapat daerah kosong (gap). antar kelas sebesar satu (dtentang = 1). Untuk Ada. Gap beberapa istilahtersebut yang perlu kita ketahui Nilai Frek menentukan tepi kelas sedemikian rupa tabel frekuensi kelompok yaitudibuat : sehingga kelas tak terputus. 1. Batas Kelas (Class antar Limits) 32 – 40 2 Untuk itu interval gap (d) kelas harus dibagi dua § Ba = Batas 41 – 49 6 § Bb = Batas bawah interval kelas 50 – 58 8 59 – 67 14 68 – 76 10 77 – 85 7 86 – 94 3 2. Batas Nyata Kelas / Tepi Kelas Perhatikan illustrasi berikut : 32 – 40 31, 5 ? ? ? 41 – 49 40, 5 32 – 40 50 – 58 49, 5 41 – 49 58, 5 50 – 58 Tepi Tepi Bawah Atas Ta Atas Ta = Tepi atas =Bawah Ba + ½d Batas bawah 59 – 67 Tepi Atas Tb = Tepi bawah Tb = Bb – ½d Di buku yang berbeda : Ta dilambangkan dengan U (Upper) dan Tb dilambangkan dengan L (Lower)

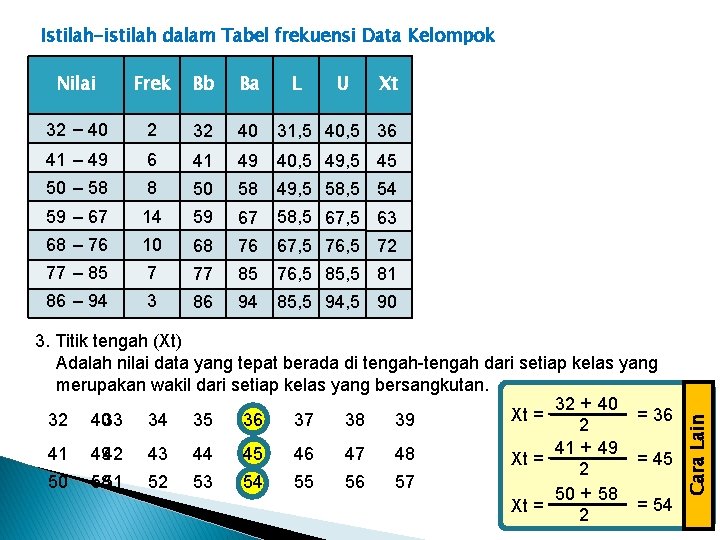
Istilah-istilah dalam Tabel frekuensi Data Kelompok Nilai Frek Bb Ba U 32 – 40 2 32 40 31, 5 40, 5 36 41 – 49 6 41 49 40, 5 49, 5 45 50 – 58 8 50 58 49, 5 58, 5 54 59 – 67 14 59 67 58, 5 67, 5 63 68 – 76 10 68 76 67, 5 76, 5 72 77 – 85 7 77 85 76, 5 85, 5 81 86 – 94 3 86 94 85, 5 94, 5 90 Xt 3. Titik tengah (Xt) Adalah nilai data yang tepat berada di tengah-tengah dari setiap kelas yang merupakan wakil dari setiap kelas yang bersangkutan. 32 + 40 = 36 Xt = 32 4033 34 35 36 37 38 39 2 41 + 49 41 4942 43 44 45 46 47 48 = 45 Xt = 2 50 5851 52 53 54 55 56 57 50 + 58 = 54 Xt = 2 Cara Lain L

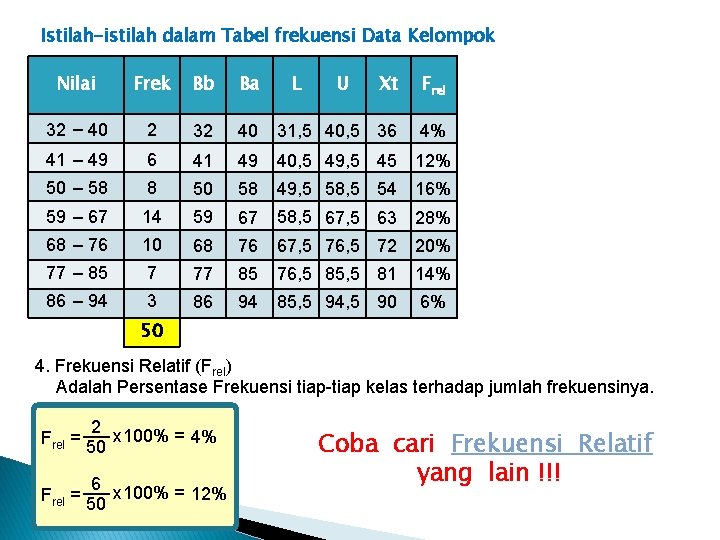
Istilah-istilah dalam Tabel frekuensi Data Kelompok Nilai Frek Bb Ba 32 – 40 2 32 41 – 49 6 50 – 58 L U Xt Frel 40 31, 5 40, 5 36 4% 41 49 40, 5 49, 5 45 12% 8 50 58 49, 5 58, 5 54 16% 59 – 67 14 59 67 58, 5 67, 5 63 28% 68 – 76 10 68 76 67, 5 76, 5 72 20% 77 – 85 7 77 85 76, 5 85, 5 81 14% 86 – 94 3 86 94 85, 5 94, 5 90 6% 50 4. Frekuensi Relatif (Frel) Adalah Persentase Frekuensi tiap-tiap kelas terhadap jumlah frekuensinya. Frel = 2 x 100% = 4% 50 Frel = 6 x 100% = 12% 50 Coba cari Frekuensi Relatif yang lain !!!

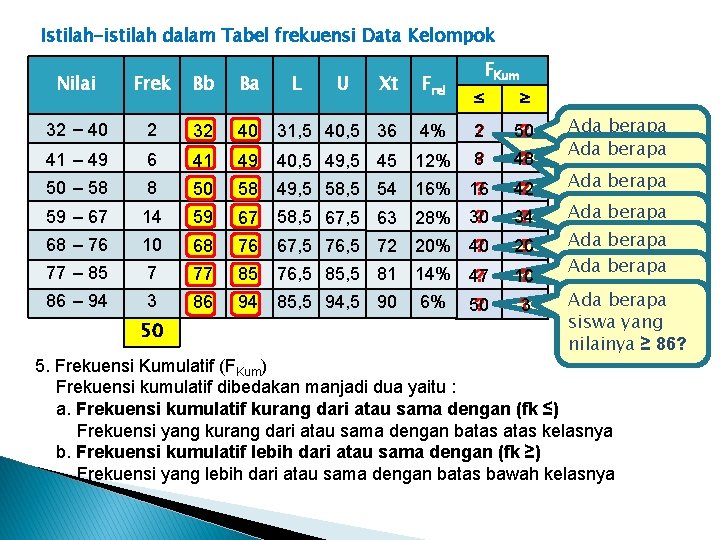
Istilah-istilah dalam Tabel frekuensi Data Kelompok Nilai Frek Bb Ba 32 – 40 2 32 41 – 49 6 50 – 58 L U Xt Frel 40 31, 5 40, 5 36 41 8 59 – 67 FKum ≤ ≥ 4% 2 ? 50 ? 49 40, 5 49, 5 45 12% 8 ? 48 ? 50 58 49, 5 58, 5 54 16% 16 ? 42 ? 14 59 67 ? 58, 5 67, 5 63 28% 30 34 ? 68 – 76 10 68 76 67, 5 76, 5 72 20% 40 ? 20 ? 77 – 85 7 77 85 10 ? 86 – 94 3 86 94 76, 5 85, 5 81 14% 47 ? 85, 5 94, 5 90 6% 50 ? 50 3 ? Ada Jika berapa tabel ini siswa yang Ada berapa adalah tabel nilainya ≥dari 32? siswa yang nilaiberapa IPA Ada nilainya ≤ 41? ≥ 49? 50 siswa, siswa yang. Ada berapa siswa nilainya ≤ 50? ≥ 58? siswa yangberapa Ada nilainya ≤≤ 59? ≥ 67? nilainya 40? siswa yang Ada berapa nilainya ≤ 68? ≥ 76? siswa yang Ada berapa nilainya ≤ 77? ≥ 85? siswa yang nilainya ≥ ≤ 86? 94? 5. Frekuensi Kumulatif (FKum) Frekuensi kumulatif dibedakan manjadi dua yaitu : a. Frekuensi kumulatif kurang dari atau sama dengan (fk ≤) Frekuensi yang kurang dari atau sama dengan batas kelasnya b. Frekuensi kumulatif lebih dari atau sama dengan (fk ≥) Frekuensi yang lebih dari atau sama dengan batas bawah kelasnya

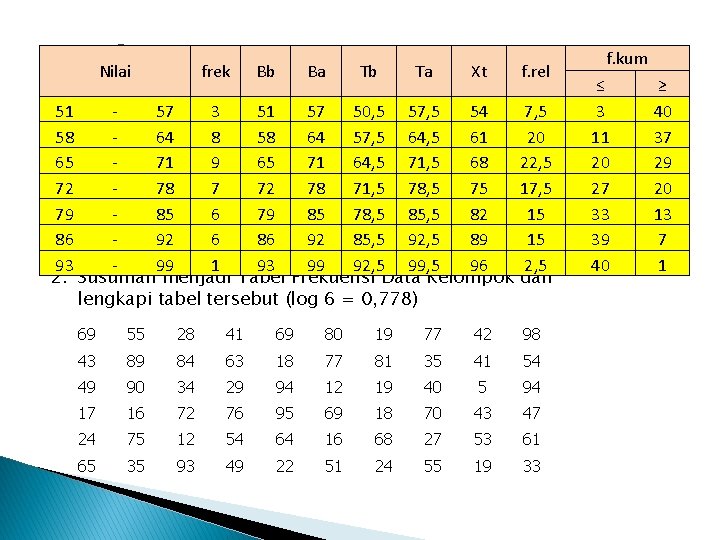
Nilai frek Latihan 2 Bb Ba Tb Ta Xt 1. menjadi Kelompok 51 Susunlah 57 3 Tabel 51 Frekuensi 57 50, 5 Data 57, 5 54 tabel tersebut 0, 602) 58 lengkapi 64 8 58 (log 644 =57, 5 64, 5 61 65 64 -51 64 71 83 9 90 65 71 6764, 568 71, 5 68 66 58 95 72 77 -75 71 78 65 7 91 72 78 7071, 562 78, 5 75 87 83 86 79 76 -72 80 85 62 6 56 79 85 5978, 571 85, 5 82 92 62 88 86 69 -57 72 92 60 6 68 86 92 8285, 585 92, 5 89 73 75 84 93 99 1 93 99 92, 5 99, 5 96 2. Susunlah menjadi Tabel Frekuensi Data Kelompok lengkapi tabel tersebut (log 6 = 0, 778) f. rel dan 7, 5 20 22, 5 17, 5 15 15 2, 5 dan 69 55 28 41 69 80 19 77 42 98 43 89 84 63 18 77 81 35 41 54 49 90 34 29 94 12 19 40 5 94 17 16 72 76 95 69 18 70 43 47 24 75 12 54 64 16 68 27 53 61 65 35 93 49 22 51 24 55 19 33 f. kum ≤ Nilai 3 51 11 - 57 58 - 64 20 65 - 71 27 72 - 78 79 33 - 85 86 39 - 92 93 40 - 99 ≥ frek 40 337 8 29 9 20 7 613 67 11

GRAFIK DAN DIAGRAM Tujuan penyajian data dalam bentuk diagram atau grafik Agar dapat memberikan informasi secara visual dengan cepat. Kegunaan : q Untuk memperjelas dan mempertegas penyajian data q Untuk mempercepat pengertian karena lebih mudah membaca gambar daripada membaca angka-angka dalam daftar q Mengurangi kejemuan melihat angka-angka q Menunjukkan arti secara menyeluruh q Memperbandingkan data secara visual

Ketentuan yang harus diperhatikan dalam membuat diagram atau grafik 1. Judul diagram atau grafik diletakkan di tengah-tengah bagian atas gambar sehingga simetris 2. Judul harus menerangkan maksud diagram atau grafik 3. Perbandingan antara tinggi dan panjang harus serasi (tak terlalu panjang/tinggi) 4. Penggunaan skala harus tepat sehingga dapat memberikan gambaran suatu perbandingan yang baik 5. Keterangan atau catatan sebagai penjelasan terhadap simbol-simbol dan warna diletakkan di bawah atau samping gambar 6. Keterangan pada skala vertikal dan horisontal harus jelas 7. Diagram harus bersih dan rapi

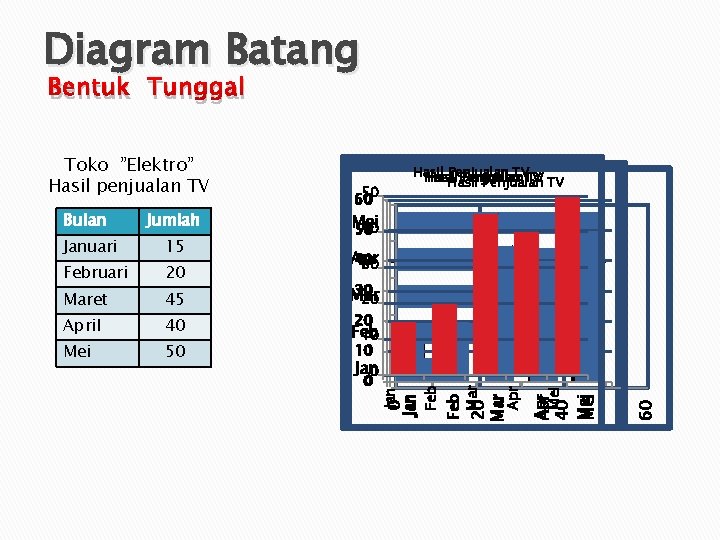
Diagram Batang Bentuk Tunggal Mei 40 50 Januari 15 Februari 20 Maret 45 30 Mar 20 April 40 Mei 50 Feb 10 Apr 40 30 20 10 60 Mei Mei 40 Apr Apr Mar Feb 0 0 Mar 20 Jan 0 Feb Jumlah 50 60 Jan Bulan Hasil Penjualan TVTV Hasil Penjualan TV TV Hasil Penjualan 0 Jan Toko ”Elektro” Hasil penjualan TV

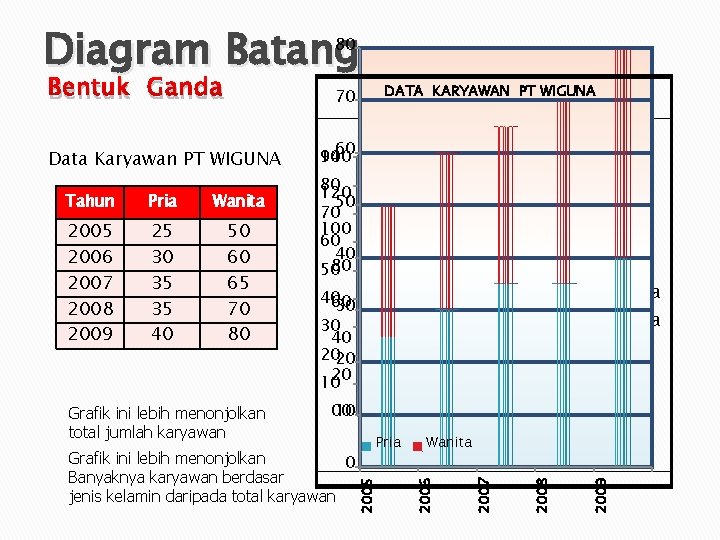
Diagram Batang 80 DATA KARYAWAN PT WIGUNA 70 Grafik ini lebih menonjolkan total jumlah karyawan Wanita Pria 40 60 30 30 40 2020 20 10 Pria Wanita 010 0 Grafik ini lebih menonjolkan 0 Banyaknya karyawan berdasar jenis kelamin daripada total karyawan Pria Wanita 2009 50 60 65 70 80 2008 2009 25 30 35 35 40 2008 2005 2006 2007 2008 2009 2007 Wanita 2007 Pria 80 120 50 70 100 60 40 80 50 2005 Tahun 140 9060 2005 Data Karyawan PT WIGUNA DATA KARYAWAN PT WIGUNA 2006 Bentuk Ganda

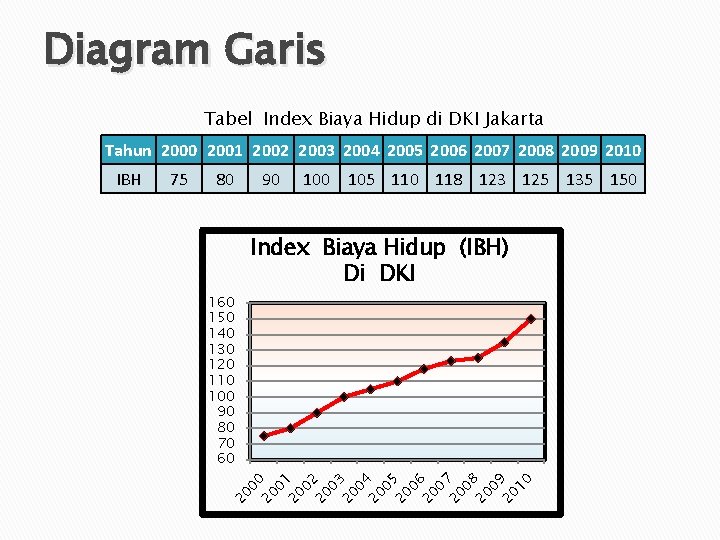
Diagram Garis Tabel Index Biaya Hidup di DKI Jakarta Tahun 2000 2001 2002 2003 2004 2005 2006 2007 2008 2009 2010 80 90 105 110 118 123 125 135 150 Index Biaya Hidup (IBH) Di DKI 160 150 140 130 120 110 100 90 80 70 60 00 20 01 20 02 20 03 20 04 20 05 20 06 20 07 20 08 20 09 20 10 75 20 IBH

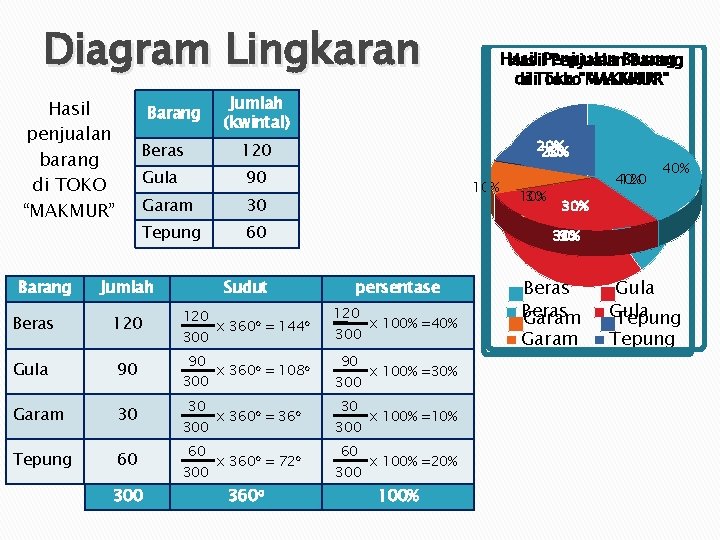
Diagram Lingkaran Hasil penjualan barang di TOKO “MAKMUR” Barang Hasil. Penjualan. Barang didi. Toko"MAKMUR" Jumlah (kwintal) Beras 120 Gula 90 Garam 30 Tepung 60 20% 60 10% 30 40% 120 40% 30% 90 Jumlah Sudut persentase Beras 120 x 360 o = 144 o 300 120 x 100% =40% 300 Gula 90 90 x 360 o = 108 o 300 90 x 100% =30% 300 Garam 30 30 x 360 o = 36 o 300 30 x 100% =10% 300 Tepung 60 60 x 360 o = 72 o 300 60 x 100% =20% 300 360 o 100% Beras Garam Gula Tepung

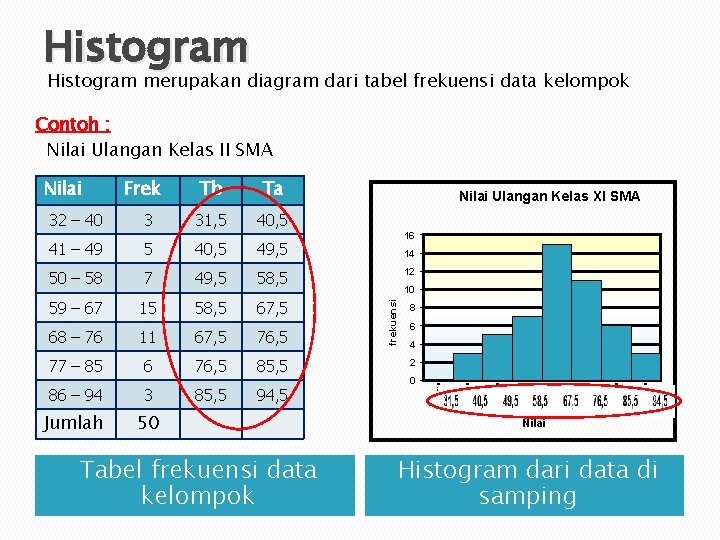
Histogram merupakan diagram dari tabel frekuensi data kelompok Contoh : Nilai Ulangan Kelas II SMA 49, 5 50 – 58 7 49, 5 58, 5 59 – 67 15 58, 5 67, 5 68 – 76 11 67, 5 76, 5 77 – 85 6 76, 5 85, 5 86 – 94 3 85, 5 94, 5 Jumlah 50 Tabel frekuensi data kelompok 14 12 10 8 6 4 2 0 94, 5 40, 5 85, 5 5 76, 5 41 – 49 16 67, 5 40, 5 58, 5 31, 5 Nilai Ulangan Kelas XI SMA 49, 5 Ta 40, 5 3 Tb 31, 5 32 – 40 Frek frekuensi Nilai Histogram dari data di samping

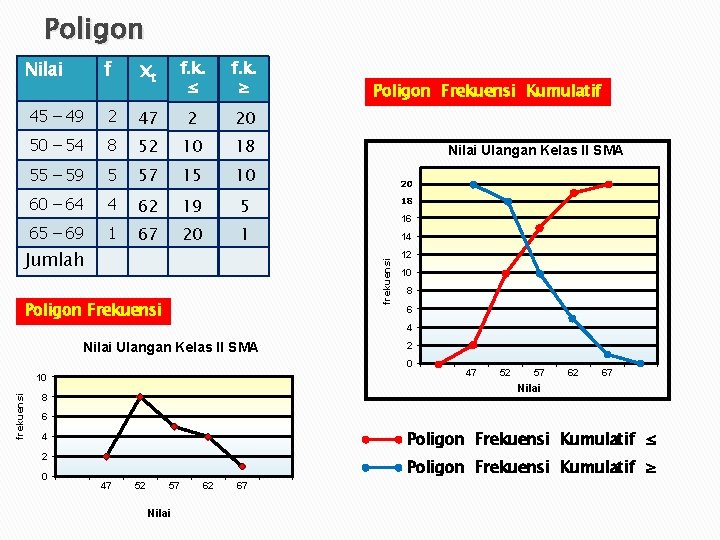
Poligon xt f. k. ≤ f. k. ≥ 45 – 49 2 47 2 20 50 – 54 8 52 10 18 55 – 59 5 57 15 10 60 – 64 4 62 19 5 65 – 69 1 67 20 1 Jumlah Poligon Frekuensi Kumulatif Nilai Ulangan Kelas II SMA 20 18 16 14 frekuensi f Nilai Poligon Frekuensi 12 10 8 6 4 Nilai Ulangan Kelas II SMA 2 0 frekuensi 10 47 52 57 62 67 Nilai 8 6 Poligon Frekuensi Kumulatif ≤ 4 2 0 Poligon Frekuensi Kumulatif ≥ 47 52 57 Nilai 62 67

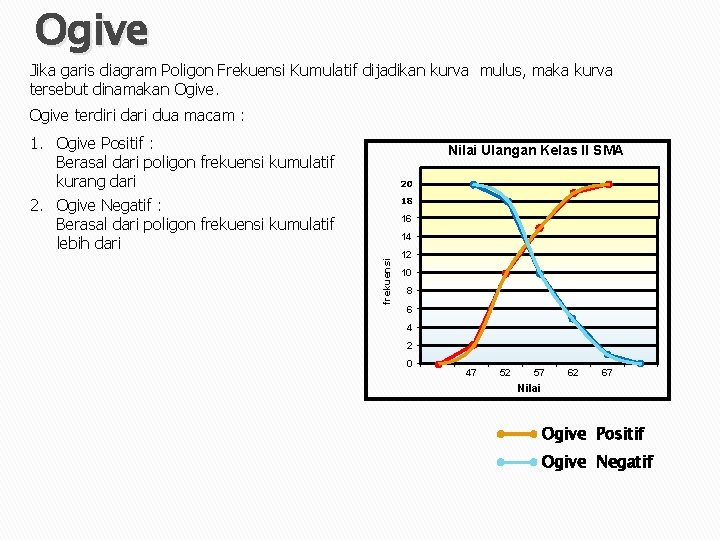
Ogive Jika garis diagram Poligon Frekuensi Kumulatif dijadikan kurva mulus, maka kurva tersebut dinamakan Ogive terdiri dari dua macam : 1. Ogive Positif : Berasal dari poligon frekuensi kumulatif kurang dari 2. Ogive Negatif : Berasal dari poligon frekuensi kumulatif lebih dari Nilai Ulangan Kelas II SMA 20 18 16 frekuensi 14 12 10 8 6 4 2 0 47 52 57 62 67 Nilai Ogive Positif Ogive Negatif

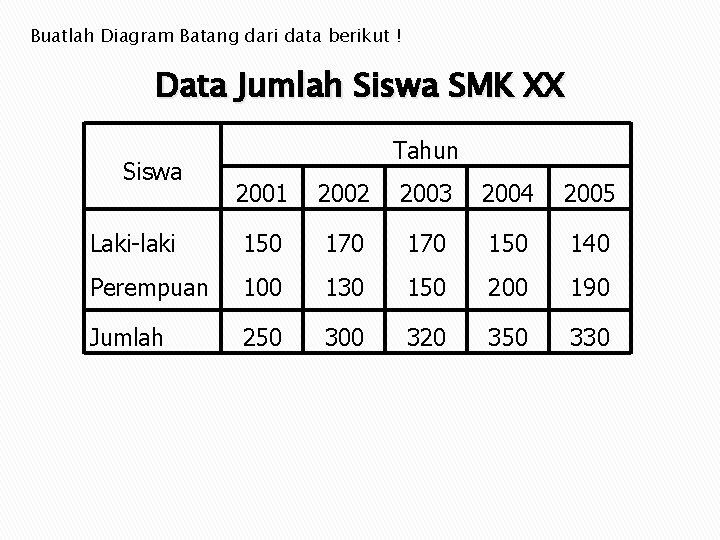
Buatlah Diagram Batang dari data berikut ! Data Jumlah Siswa SMK XX Siswa Tahun 2001 2002 2003 2004 2005 Laki-laki 150 170 150 140 Perempuan 100 130 150 200 190 Jumlah 250 300 320 350 330

Buatlah Diagram Lingkaran dari data berikut ! Data Peserta Ekstrakurikuler Jenis Ekstrakurikuler Pramuka Patroli Keamanan Sekolah Seni Tari Karya Ilmiah Remaja Tampilkan dalam bentuk persentase f 20 15 10 5

Tugas !! Buatlah Histogram, Poligon Frekuensi dan Ogive Positif dari data berikut ! Usia Penduduk RT 12 Tahun 1999 Nilai 15 – 19 20 – 24 25 – 29 30 – 34 35 – 39 f 8 12 15 10 5

4. UKURAN PEMUSATAN (Tendensi Sentral) Ada tiga Ukuran Pemusatan yang akan kita pelajari yaitu : q Mean q Median q Modus Mean = Rata-rata data Median = Nilai data yang berada di tengah setelah data diurutkan Modus = Nilai data yang frekuensinya terbanyak atau Nilai data yang paling sering muncul

Mean 1. Pada Data Tunggal Rata-rata Hitung Jika nilai data x 1, x 2, x 3, x 4, …. , xn dengan banyaknya data n, maka Mean dirumuskan : x= x 1 + x 2 + x 3 + x 4 +…. + xn n Contoh : Tentukan rata-rata dari rangkaian data 7, 5, 8, 6, 9, 7 Jawab : Banyaknya data atau n = 6, maka x= 7+5+8+6+9+7 6 = 42 6 = 7 Jadi rata-rata dari data tersebut adalah 7 = xi n

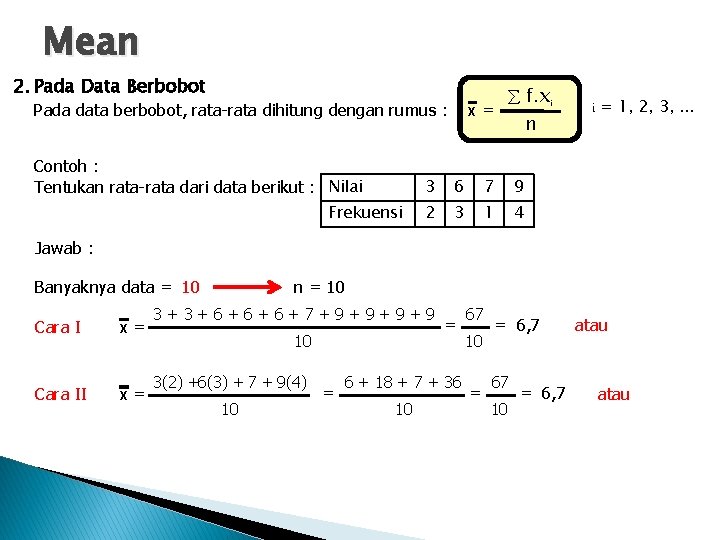
Mean 2. Pada Data Berbobot Pada data berbobot, rata-rata dihitung dengan rumus : Contoh : Tentukan rata-rata dari data berikut : Nilai Frekuensi x= f. xi n 3 6 7 9 2 3 1 4 i = 1, 2, 3, . . . Jawab : Banyaknya data = 10 Cara II x= x= n = 10 3+3+6+6+6+7+9+9 10 3(2) +6(3) + 7 + 9(4) 10 = = 6 + 18 + 7 + 36 10 67 10 = = 6, 7 67 10 = 6, 7 atau

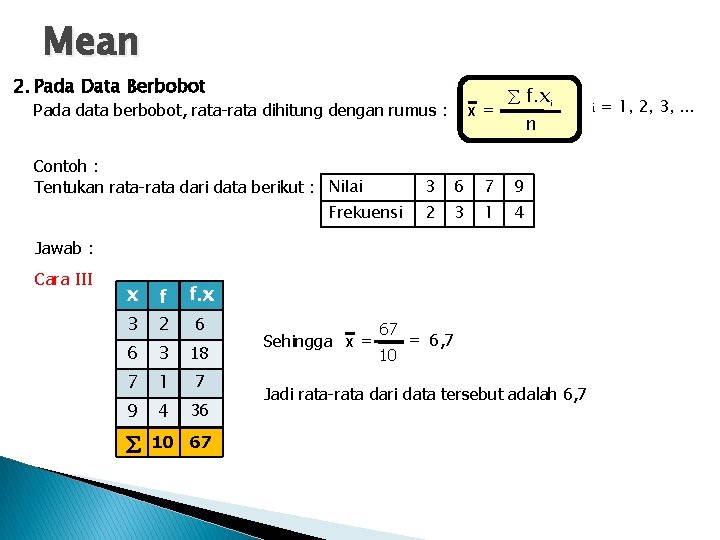
Mean 2. Pada Data Berbobot Pada data berbobot, rata-rata dihitung dengan rumus : Contoh : Tentukan rata-rata dari data berikut : Nilai Frekuensi x= f. xi n 3 6 7 9 2 3 1 4 Jawab : Cara III x f. x 3 f 2 6 3 18 7 1 7 9 4 36 6 10 67 Sehingga x = 67 10 = 6, 7 Jadi rata-rata dari data tersebut adalah 6, 7 i = 1, 2, 3, . . .

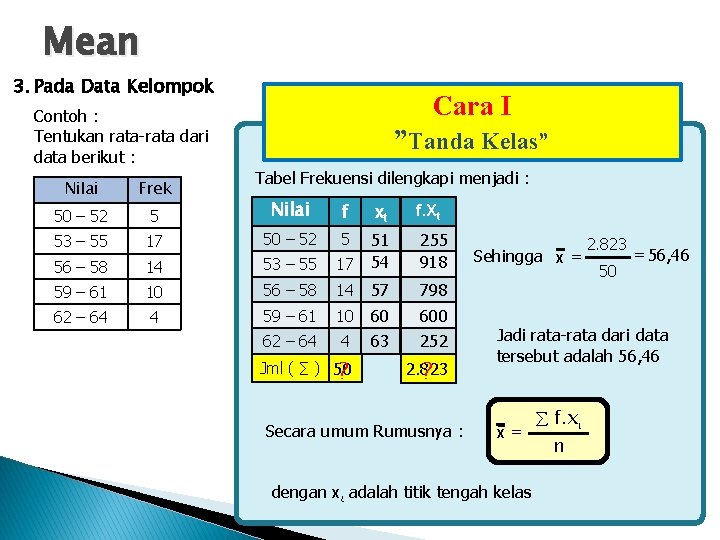
Mean 3. Pada Data Kelompok Cara I Contoh : Tentukan rata-rata dari data berikut : ”Tanda Kelas” Tabel Frekuensi dilengkapi menjadi : Nilai Frek 50 – 52 5 Nilai f xt f. Xt 53 – 55 17 50 – 52 5 56 – 58 14 53 – 55 17 51 54 255 918 59 – 61 10 56 – 58 14 57 798 62 – 64 4 59 – 61 10 62 – 64 4 60 63 600 252 Jml ( ∑ ) 50 ? 2. 823 ? Secara umum Rumusnya : Sehingga x = 2. 823 50 = 56, 46 Jadi rata-rata dari data tersebut adalah 56, 46 x= dengan xt adalah titik tengah kelas f. xt n

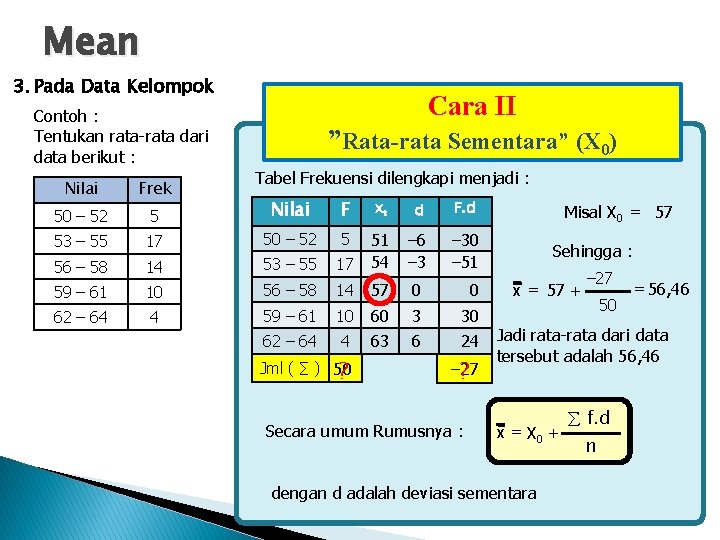
Mean 3. Pada Data Kelompok Cara II Contoh : Tentukan rata-rata dari data berikut : ”Rata-rata Sementara” (X 0) Tabel Frekuensi dilengkapi menjadi : Nilai Frek 50 – 52 5 Nilai F xt d F. d 53 – 55 17 50 – 52 5 14 53 – 55 17 51 54 – 6 – 30 – 51 59 – 61 10 56 – 58 14 57 0 0 62 – 64 4 59 – 61 10 62 – 64 4 60 63 3 6 30 24 56 – 58 Jml ( ∑ ) 50 ? – 27 ? Secara umum Rumusnya : Misal X 0 = 57 Sehingga : x = 57 + – 27 50 = 56, 46 Jadi rata-rata dari data tersebut adalah 56, 46 x = X 0 + dengan d adalah deviasi sementara f. d n

Latihan 4. Diperoleh hasil pengukuran 40 1. Tentukan rata-rata dari hasil batang kawat (dalam cm) ulangan 10 siswa berikut : 5, 5 4, 2, 8, 8, 5, 7, 5, 6, 7, 3 4 7 5 5 6 3 9 7 8 5 2. Tentukan rata-rata dari panjang 5 7 4 5 4 4 8 6 5 5 8 batang kayu dalam cm : 32, 5 6 6 8 7 4 5 4 4 6 6 24, 32, 42, 28, 41, 35, 23 3 3 6 5 9 8 9 5 5 3 3. Tentukan nilai rata-rata dari hasil ulangan Matematika 40 Tentukan rata-rata dari data siswa sbb : tersebut! 5, 6 Nilai F 4 5 6 7 8 6 5 4 5, 7

5. 6. 7. 8. 9. Nilai rata-rata 9 anak adalah 7. Jika ada satu anak baru mempunyai nilai 6, berapa nilai rata-rata kesepuluh anak tersebut ? Nilai rata-rata 7 anak adalah 8. Jika ditambah satu anak yang bernilai 10, nilai rata-rata nya menjadi …. Nilai rata-rata 11 anak adalah 6. Dengan masuknya seorang anak lagi, rata-ratanya menjadi 6, 25. Tentukan nilai anak yang baru masuk ! Nilai rata-rata 14 anak adalah 7. Jika ada seorang anak baru dimasukkan, nilai rata-ratanya menjadi 7, 2. Tentukan nilai anak baru tersebut ! Nilai rata-rata suatu kelas yang terdiri dari 36 siswa adalah 7, 5. Jika salah satu anak keluar, maka rata-ratanya menjadi 7, 6. Berapa nilai anak yang keluar tersebut ?

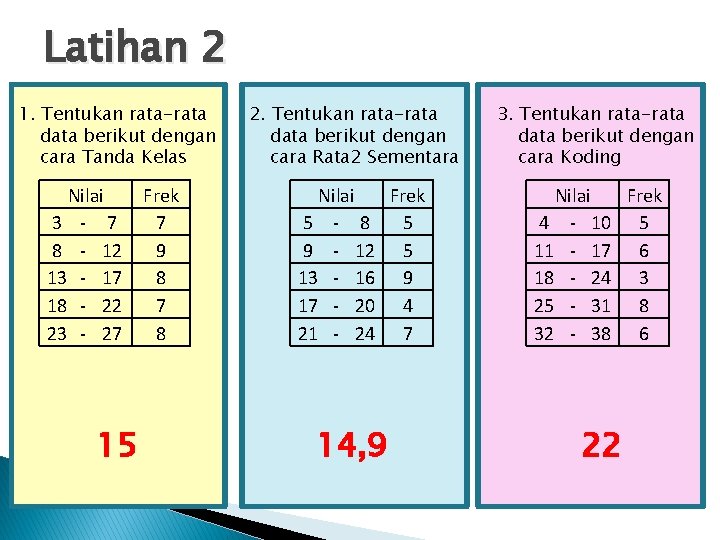
Latihan 2 1. Tentukan rata-rata data berikut dengan cara Tanda Kelas Nilai 3 - 7 8 - 12 13 - 17 18 - 22 23 - 27 15 Frek 7 9 8 7 8 2. Tentukan rata-rata data berikut dengan cara Rata 2 Sementara Nilai Frek 5 - 8 5 9 - 12 5 13 - 16 9 17 - 20 4 21 - 24 7 14, 9 3. Tentukan rata-rata data berikut dengan cara Koding Nilai Frek 4 - 10 5 11 - 17 6 18 - 24 3 25 - 31 8 32 - 38 6 22

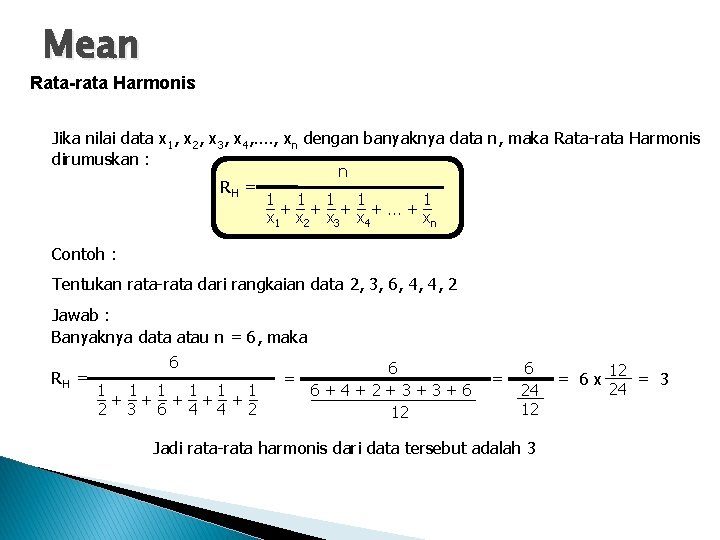
Mean Rata-rata Harmonis Jika nilai data x 1, x 2, x 3, x 4, …. , xn dengan banyaknya data n, maka Rata-rata Harmonis dirumuskan : RH = n 1 1 1 – + – +. . . + – x 1 x 2 x 3 x 4 xn Contoh : Tentukan rata-rata dari rangkaian data 2, 3, 6, 4, 4, 2 Jawab : Banyaknya data atau n = 6, maka RH = 6 1 1 1 –+–+–+– 2 3 6 4 4 2 = 6 6 12 = = 6 x ___ = 3 24 6+4+2+3+3+6 24 ___________ 12 12 Jadi rata-rata harmonis dari data tersebut adalah 3

Median merupakan nilai data yang berada di tengah setelah data diurutkan 1. Pada Data Array Pada data Array, data diurutkan terlebih dahulu Contoh : Tentukan median dari data berikut : a. 3, 5, 8, 5, 6, 2, 7, 6, 5, 7, 9 b. 4, 7, 8, 7, 7, 5, 6, 6, 3, 4, 8, 9 Jawab : a. Data diurutkan menjadi : 2, 3, 5, 5, 5, 6, 6, 7, 7, 8, 9 2, Median 3, 5, 5, = 5, 6, 6, 7, 7, 8, 9 b. Data diurutkan menjadi : 3, 4, 4, 5, 6, 6, 7, 7, 7, 8, 8, 9 Median = 6 + 7 = 13 = 6, 5 2 2 Median terletak diantara 6 dan 7

Latihan Median Tentukan median dari data-data berikut a. 5, 6, 6, 7, 5, 8, 9, 6 b. 5, 8, 8, 9, 4, 7, 5, 9, 7, 7, 8, 6, 8, 5, 9 c. 7, 3, 6, 7, 8, 2, 2, 6, 3, 6 6 7 6

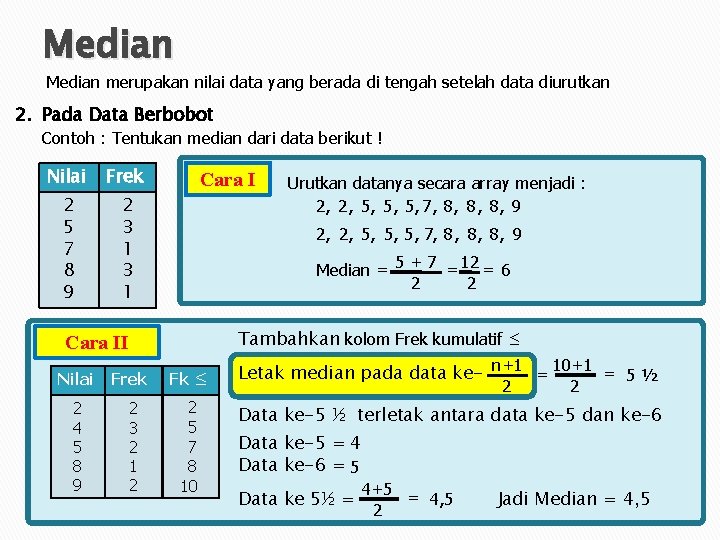
Median merupakan nilai data yang berada di tengah setelah data diurutkan 2. Pada Data Berbobot Contoh : Tentukan median dari data berikut ! Nilai Frek 2 5 7 8 9 2 3 1 Cara I Urutkan datanya secara array menjadi : 2, 2, 5, 5, 5, 7, 8, 8, 8, 9 Median = 5 + 7 = 12 = 6 2 2 Tambahkan kolom Frek kumulatif ≤ Cara II Nilai Frek Fk ≤ 2 4 5 8 9 2 3 2 1 2 2 5 7 8 10 Letak median pada data ke- n+1 = 10+1 = 5 ½ 2 2 Data ke-5 ½ terletak antara data ke-5 dan ke-6 Data ke-5 = 4 Data ke-6 = 5 Data ke 5½ = 4+5 = 4, 5 2 Jadi Median = 4, 5

Latihan Median Hasil tes Matematika sebanyak 25 orang diperoleh nilai sebagai berikut : Nilai 8 6 9 3 4 5 Frekuensi 3 8 5 2 4 3 Tentukan Median dari data tersebut 9

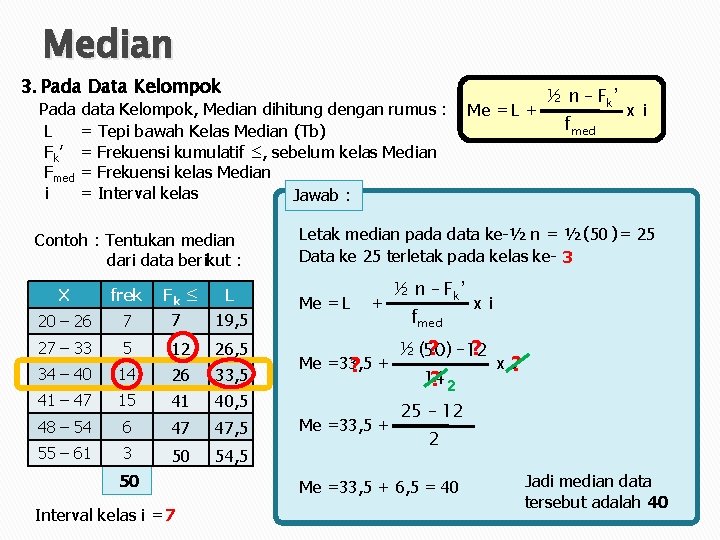
Median 3. Pada Data Kelompok Pada data Kelompok, Median dihitung dengan rumus : L = Tepi bawah Kelas Median (Tb) Fk’ = Frekuensi kumulatif ≤, sebelum kelas Median Fmed = Frekuensi kelas Median i = Interval kelas Jawab : Contoh : Tentukan median dari data berikut : X frek Fk ≤ L 20 – 26 7 7 19, 5 27 – 33 5 12 26, 5 34 – 40 14 26 33, 5 41 – 47 15 41 40, 5 48 – 54 6 47 47, 5 55 – 61 3 50 54, 5 50 Interval kelas i = 7 Me = L + ½ n – Fk ’ fmed x i Letak median pada data ke-½ n = ½ (50 ) = 25 Data ke 25 terletak pada kelas ke- 3 Me = L + Me =33, 5 ? + Me =33, 5 + ½ n – Fk ’ fmed x i ½ (50 ? ) – 12 ? 14 ? 2 x? 7 25 – 12 2 Me =33, 5 + 6, 5 = 40 Jadi median data tersebut adalah 40

Latihan Median Tentukan median dari data berikut : a. Berat (kg) Jumlah karung 5 – 10 7 11 – 16 9 17 – 22 5 23 – 28 4 29 – 34 3 35 – 40 2 Median = 15, 83 b. Data 2– 6 7 – 11 12 – 16 17 – 21 22 – 26 f 2 6 5 4 3 Median = 13, 5

Modus Adalah : Ø Nilai data yang paling sering muncul Ø Nilai data yang frekuensinya paling besar 1. Pada Data Array Contoh : Tentukan Modus dari rangkaian data berikut ! Mo = 8 a) 7, 5, 8, 6, 9, 8, 10 Mo = 5 dan 7 b) 7, 5, 6, 8, 3, 5, 7, 9, 10 Mo = tidak ada c) 5, 7, 6, 9, 8, 11

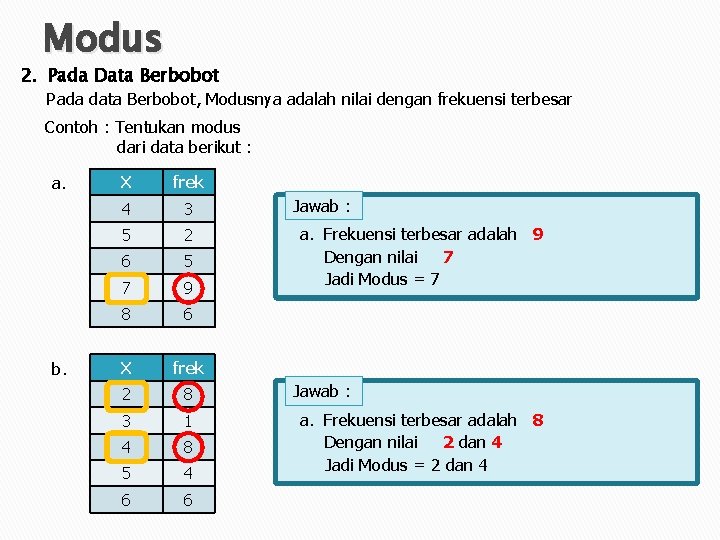
Modus 2. Pada Data Berbobot Pada data Berbobot, Modusnya adalah nilai dengan frekuensi terbesar Contoh : Tentukan modus dari data berikut : a. b. X frek 4 3 5 2 6 5 7 9 8 6 X frek 2 8 3 1 4 8 5 4 6 6 Jawab : a. Frekuensi terbesar adalah 9 Dengan nilai 7 Jadi Modus = 7 Jawab : a. Frekuensi terbesar adalah 8 Dengan nilai 2 dan 4 Jadi Modus = 2 dan 4

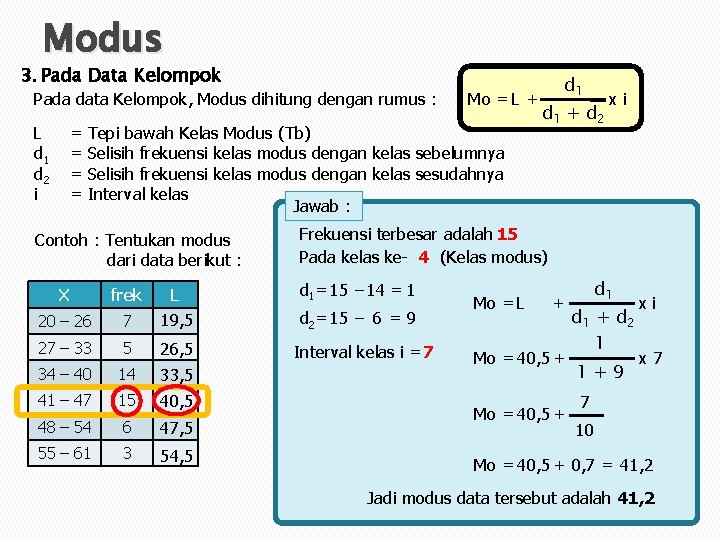
Modus 3. Pada Data Kelompok Pada data Kelompok, Modus dihitung dengan rumus : L d 1 d 2 i = = Mo = L + Tepi bawah Kelas Modus (Tb) Selisih frekuensi kelas modus dengan kelas sebelumnya Selisih frekuensi kelas modus dengan kelas sesudahnya Interval kelas Jawab : Contoh : Tentukan modus dari data berikut : d 1 + d 2 xi Frekuensi terbesar adalah 15 Pada kelas ke- 4 (Kelas modus) X frek L d 1= 15 – 14 = 1 20 – 26 7 19, 5 d 2= 15 – 6 = 9 27 – 33 5 26, 5 34 – 40 14 33, 5 41 – 47 15 40, 5 48 – 54 6 47, 5 55 – 61 3 54, 5 Interval kelas i = 7 Mo = L + Mo = 40, 5 + d 1 + d 2 1 1+9 xi x 7 7 10 Mo = 40, 5 + 0, 7 = 41, 2 Jadi modus data tersebut adalah 41, 2

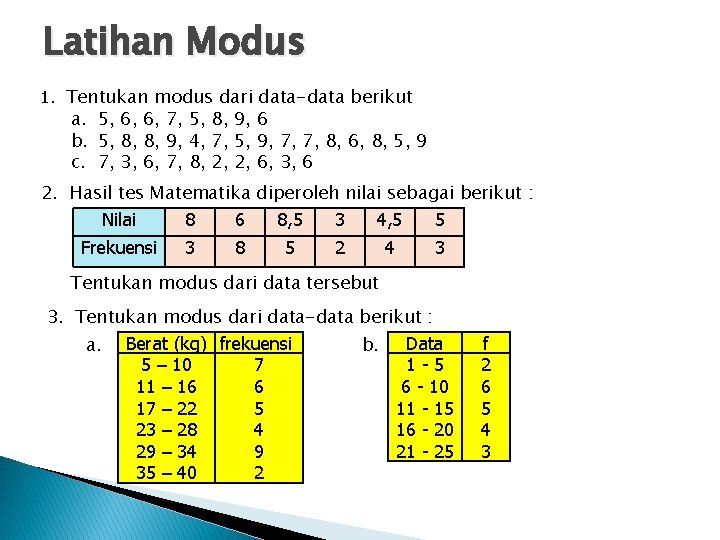
Latihan Modus 1. Tentukan modus dari data-data berikut a. 5, 6, 6, 7, 5, 8, 9, 6 b. 5, 8, 8, 9, 4, 7, 5, 9, 7, 7, 8, 6, 8, 5, 9 c. 7, 3, 6, 7, 8, 2, 2, 6, 3, 6 2. Hasil tes Matematika diperoleh nilai sebagai berikut : Nilai 8 6 8, 5 3 4, 5 5 Frekuensi 3 8 5 2 4 3 Tentukan modus dari data tersebut 3. Tentukan modus dari data-data berikut : a. Berat (kg) frekuensi 5 – 10 7 11 – 16 6 17 – 22 5 23 – 28 4 29 – 34 9 35 – 40 2 b. Data 1 -5 6 - 10 11 - 15 16 - 20 21 - 25 f 2 6 5 4 3

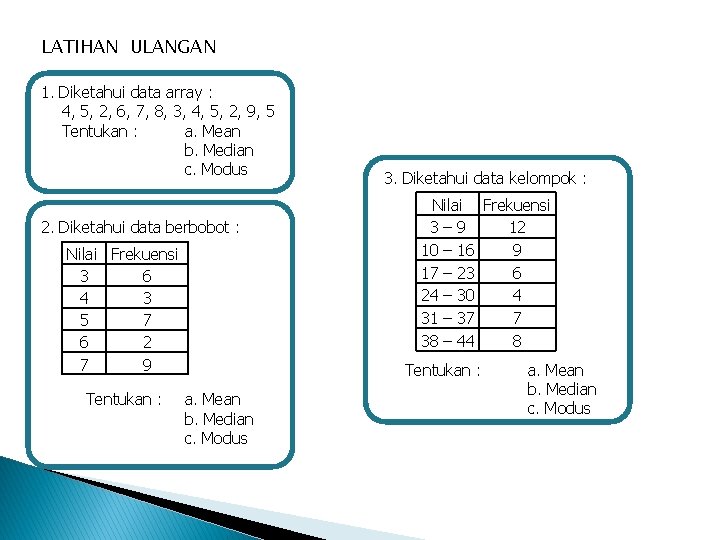
LATIHAN ULANGAN 1. Diketahui data array : 4, 5, 2, 6, 7, 8, 3, 4, 5, 2, 9, 5 Tentukan : a. Mean b. Median c. Modus 2. Diketahui data berbobot : Nilai Frekuensi 3 6 4 3 5 7 6 2 7 9 Tentukan : 3. Diketahui data kelompok : Nilai Frekuensi 3– 9 12 10 – 16 9 17 – 23 6 24 – 30 4 31 – 37 7 38 – 44 8 Tentukan : a. Mean b. Median c. Modus

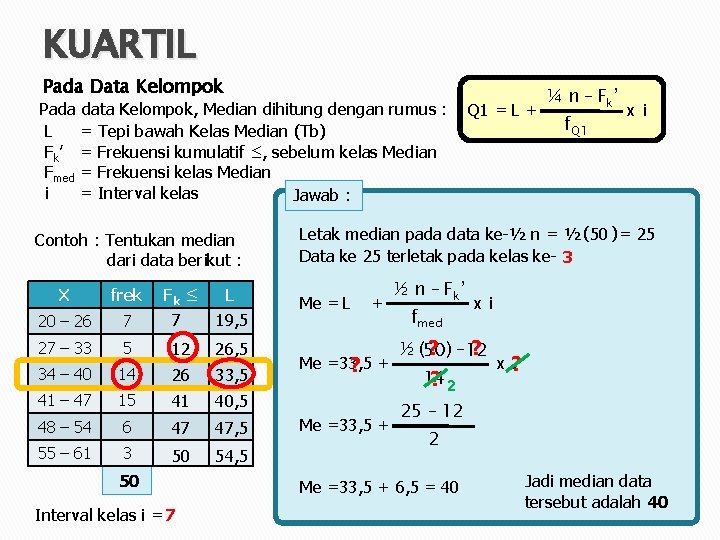
KUARTIL Pada Data Kelompok Pada data Kelompok, Median dihitung dengan rumus : L = Tepi bawah Kelas Median (Tb) Fk’ = Frekuensi kumulatif ≤, sebelum kelas Median Fmed = Frekuensi kelas Median i = Interval kelas Jawab : Contoh : Tentukan median dari data berikut : X frek Fk ≤ L 20 – 26 7 7 19, 5 27 – 33 5 12 26, 5 34 – 40 14 26 33, 5 41 – 47 15 41 40, 5 48 – 54 6 47 47, 5 55 – 61 3 50 54, 5 50 Interval kelas i = 7 Q 1 = L + ¼ n – Fk ’ f. Q 1 x i Letak median pada data ke-½ n = ½ (50 ) = 25 Data ke 25 terletak pada kelas ke- 3 Me = L + Me =33, 5 ? + Me =33, 5 + ½ n – Fk ’ fmed x i ½ (50 ? ) – 12 ? 14 ? 2 x? 7 25 – 12 2 Me =33, 5 + 6, 5 = 40 Jadi median data tersebut adalah 40