Q 1 What is numerical analysis for Input

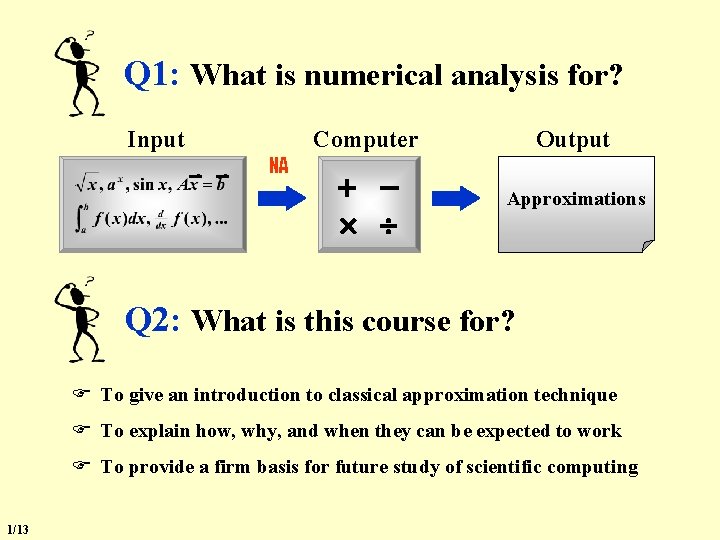
Q 1: What is numerical analysis for? Input NA Computer Output Approximations Q 2: What is this course for? F To give an introduction to classical approximation technique F To explain how, why, and when they can be expected to work F To provide a firm basis for future study of scientific computing 1/13

Chapter 1 Mathematical Preliminaries 1. 2 Roundoff Errors and Computer Arithmetic Example: Approximate = 0. 747… … Solution: Use Taylor expansion of S 4 R 4 /* Remainder */ Take | Total error | Truncation Roundoff error(by excluded included terms) < 0. 006 < 0. 0005 2 < 0. 005 = 0. 001 2/13

Chapter 1 Mathematical Preliminaries -- Roundoff Errors and Computer Arithmetic Truncation Error: the error involved in using a truncated, or finite, summation to approximate the sum of an infinite series. Roundoff Error: the error produced when performing real number calculations. It occurs because the arithmetic performed in a machine involves numbers with only a finite number of digits. Normalized decimal floating-point form of a real number: where 1 d 1 9 and 0 di 9 ( i = 2, …, k ) k-digit decimal machine number Given a real number y = 0. d 1 d 2 … dk dk+1 dk+2 … 10 n /* Chopping */ /* Rounding */ 3/13

Chapter 1 Mathematical Preliminaries -- Roundoff Errors and Computer Arithmetic Definition: If p* is an approximation to p, the absolute error is | p – p* |, and the relative error is | p – p* | / | p |, provided that p 0. Of course is more p to t significant digits I can tell that distance I is can tell that this Definition: The number p* said tomine approximate accurate ! The accuracy between two planets part’s diameter isis for which (or figures) if t is the largest nonnegative integer relates to not only 1 million light year ± 1 the 20 cm 1 cm. absolute lighterror, year. but also to the size of the exact value. Chopping: Rounding: 4/13

Chapter 1 Mathematical Preliminaries -- Roundoff Errors and Computer Arithmetic How will roundoff error affect our results? Subtraction of nearly equal numbers will cause a cancellation of significant digits. Example: a 1 = 0. 12345 and a 2 = 0. 12346 both have 5 significant digits. However, a 2 a 1 = 0. 00001 has only 1 significant digit left. Dividing by a number with small magnitude (or, equivalently, multiplying by a number with large magnitude) will cause an enlargement of the error. Remember: always simplify your formulae before you give them to your computer! 5/13

Chapter 1 Mathematical Preliminaries -- Roundoff Errors and Computer Arithmetic Example: Find the roots of x 2 + 62. 10 x + 1 = 0, using 4 -digit rounding. The roots are x 1 0. 01610723 and x 2 62. 08390. Solution: 6/13 Relative error 24% Relative error 0. 032% An alternative approach:

Chapter 1 Mathematical Preliminaries -- Roundoff Errors and Computer Arithmetic Example: Evaluate f(x) = x 3 – 6. 1 x 2 + 3. 2 x + 1. 5 at x = 4. 71 using 3 -digit arithmetic. x x 2 x 3 6. 1 x 2 3. 2 x Exact 4. 71 22. 1841 104. 487111 135. 32301 15. 072 Chopping 4. 71 22. 1 104. 134. 15. 0 Rounding 4. 71 22. 2 105. 135. 15. 1 HW: p. 27 -28 Exact = – 14. 263899; Chopping = – 13. 5; Rounding = – 13. 4 #3, 11, Relative error (Chopping) 5%; 17(b) Relative error (Rounding) 6% An alternative approach: f(x) = x 3 – 6. 1 x 2 + 3. 2 x + 1. 5 = ((x – 6. 1) x + 3. 2) x + 1. 5 Chopping = – 14. 2; Rounding = – 14. 3 Relative error (Chopping) 0. 45% Relative error (Rounding) 0. 25% 7/13 秦九韶算法 Horner’s Method

Chapter 1 Mathematical Preliminaries 1. 3 Algorithms and Convergence The following problem can be solved either the easy way or the hard way. Two trains 200 miles apart are moving toward each other; each one is going at a speed of 50 miles per hour. A fly starting on the front of one of them flies back and forth between them at a rate of 75 miles per hour. It does this until the trains collide and crush the fly to death. What is the total distance the fly has flown? The fly actually hits each train an infinite number of times before it gets crushed, and one could solve the problem the hard way with pencil and paper by summing an infinite series of distances. The easy way is as follows: Since the trains are 200 miles apart and each train is going 50 miles an hour, it takes 2 hours for the trains to collide. Therefore the fly was flying for two hours. Since the fly was flying at a rate of 75 miles per hour, the fly must have flown 150 miles. That's all there is to it. When this problem was posed to John von Neumann, he immediately replied, "150 miles. " "It is very strange, " said the poser, "but nearly everyone tries to sum the infinite series. " "What do you mean, strange? " asked Von Neumann. "That's how I did it!" 8/13

Chapter 1 Mathematical Preliminaries -- Algorithms and Convergence The Colonel's Order A COLONEL ISSUED THE FOLLOWING DIRECTIVE TO HIS EXECUTIVE OFFICERS: "Tomorrow evening at approximately 20: 00 Halley's Comet will be visible in this area; an event which occurs only every 75 years. Have the men fall out in the battalion area in fatigues, and I will explain this rare phenomenon to them. In case of rain, we will not be able to see anything, so assemble the men in theater and I will show them films of it. " EXECUTIVE OFFICER TO COMPANY COMMANDER: "By order of the Colonel, tomorrow at 20: 00, Halley's Comet will appear above the battalion area. If it rains, fall the men out in fatigues, then march to theater where this rare phenomenon will take place, something which occurs only once every 75 years. " COMPANY COMMANDER TO LIEUTENANT: "By order of the Colonel be in fatigues at 20: 00 tomorrow evening the phenomenal Halley's Comet will appear in theater. In case of rain in the battalion area, the Colonel will give another order, something which occurs once every 75 years. " LIEUTENANT TO SERGEANT: "Tomorrow at 20: 00, the Colonel will appear in theater with Halley's comet, something which happens every 75 years. If it rains, the Colonel will order the comet into the battalion area. " SERGEANT TO SQUAD: "When it rains tomorrow at 20: 00, the phenomenal 75 -year-old General Halley, accompanied by the Colonel, will drive his comet through the battalion area theater in fatigues. " 9/13

Chapter 1 Mathematical Preliminaries -- Algorithms and Convergence Definition: An algorithm that satisfies that small changes in the initial data produce correspondingly small changes in the final results is called stable; otherwise it is unstable. An algorithm is called conditionally stable if it is stable only for certain choices of initial data. Definition: Suppose that E 0 > 0 denotes an initial error and En represents the magnitude of an error after n subsequent operations. If En C n E 0, where C is a constant independent of n, then the growth of error is said to be linear. If En Cn E 0, for some C > 1, then the growth of error is called exponential. Note: Linear growth of error is usually unavoidable, and when C and E 0 are small the results are generally acceptable. Exponential growth of error should be avoided since the term Cn becomes large for even relatively small values of n. This leads to unacceptable inaccuracies, regardless of the size of E 0. 10/13

Chapter 1 Mathematical Preliminaries -- Algorithms and Convergence Example: Evaluate Method 1: This is theoretically accurate. What happened ? ! ? ? ? ? ! !! 11/13 Unstable !

Chapter 1 Mathematical Preliminaries -- Algorithms and Convergence Method 2: We may take This is theoretically equivalent to the previous formula. HW: p. 38 #7 Take Excuses for not doing homework I accidentally divided by zero and my paper burst into flames. Stable! 12/13 We just got lucky?

Chapter 1 Mathematical Preliminaries -- Algorithms and Convergence Lab 01. Numerical Summation of a Series Time Limit: 1 second; Points: 4 Produce a table of the values of the series (1) for the 3001 values of x, x = 0. 0, 0. 1, 0. 2, …, 300. All entries of the table must have an absolute error less than 1. 0 e-10. This problem is based on a problem from Hamming (1962), when mainframes were very slow by today's microcomputer standards. 13/13