Python Programming in Context Chapter 9 Objectives To

Python Programming in Context Chapter 9

Objectives • To introduce functional programming style • To practice writing recursive functions • To introduce grammars and production rules

Recursion • A self referencing solution • Base case is easily solved • Recursive step uses solution to try to solve smaller version of the problem • Sometimes easier to see with pictures

Figure 9. 1

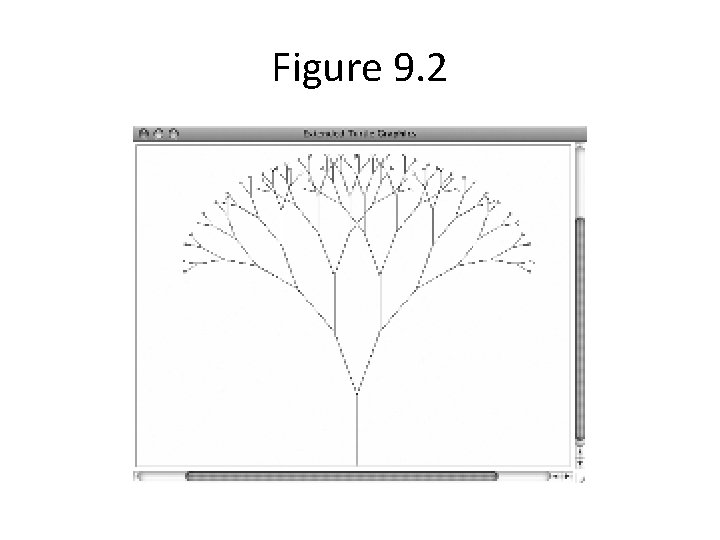
Figure 9. 2

Infinite Recursion • No base case • In theory this will continue to call itself forever • In practice, memory will eventually be completely consumed and process will stop

Listing 9. 1 def hello(): print("Hello World") hello()

Nested Squares • Base Case – Draw a simple square • Recursive Step – Draw a picture of recursive squares starting with a smaller side length

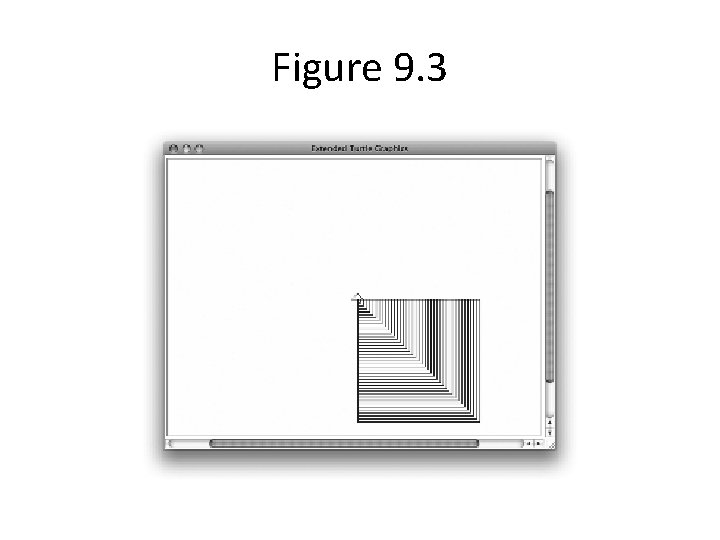
Figure 9. 3

Listing 9. 2 def draw. Square(a. Turtle, side): for i in range(4): a. Turtle. forward(side) a. Turtle. right(90) def nested. Box(a. Turtle, side): if side >= 1: draw. Square(a. Turtle, side) nested. Box(a. Turtle, side-5)

Recursive Tree • • Draw trunk Recursively draw a tree on the right Recursively draw a tree on the left Stop when the tree is sufficiently small

Listing 9. 3 def tree(t, trunk. Length): if trunk. Length < 5: return else: t. forward(trunk. Length) t. right(30) tree(t, trunk. Length-15) t. left(60) tree(t, trunk. Length-15) t. right(30) t. backward(trunk. Length)

Sierpinski Triangle • Draw triangles from triangles by connecting the midpoints of the sides • Continue to do this for each newly created triangle • Stop at a sufficient number of levels

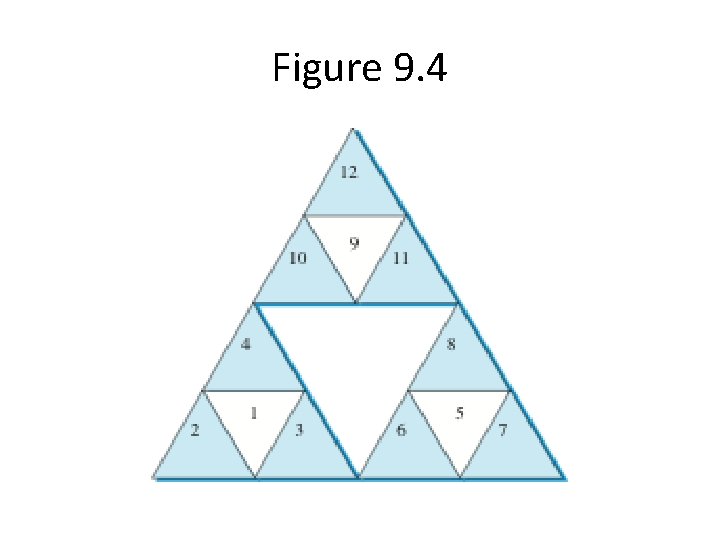
Figure 9. 4

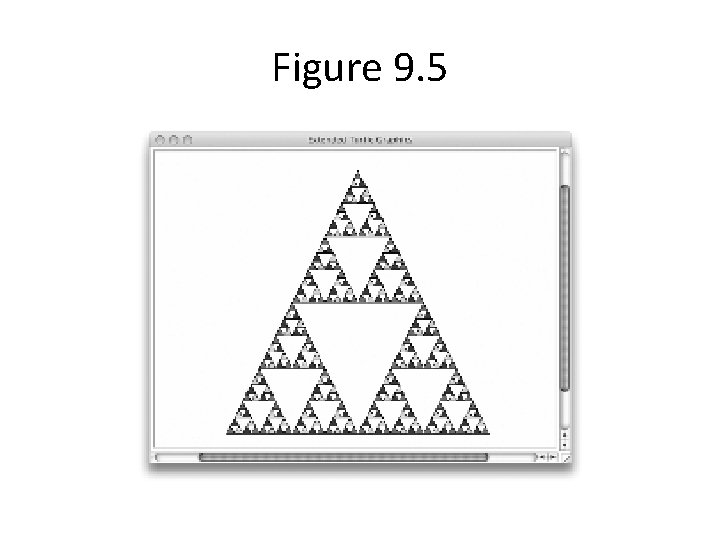
Figure 9. 5

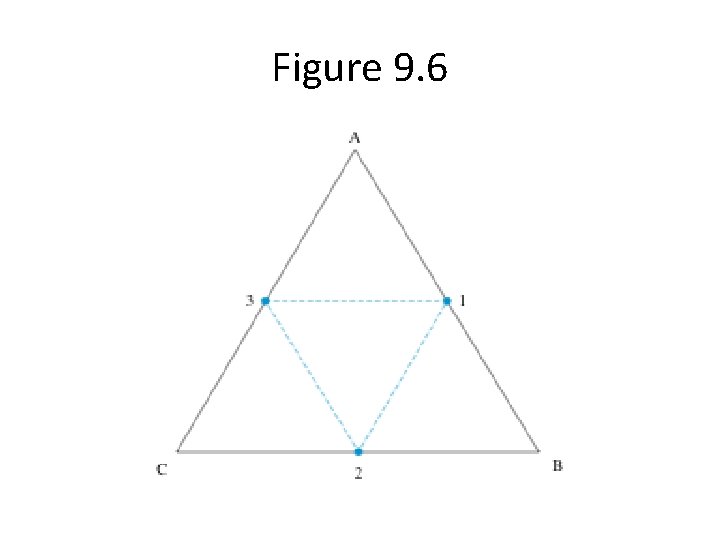
Figure 9. 6

Listing 9. 4 def draw. Triangle(t, p 1, p 2, p 3): t. up() t. goto(p 1) t. down() t. goto(p 2) t. goto(p 3) t. goto(p 1) def mid. Point(p 1, p 2): return ((p 1[0]+p 2[0])/2. 0, (p 1[1]+p 2[1])/2. 0) def sierpinski(my. Turtle, p 1, p 2, p 3, depth): if depth > 0: sierpinski(my. Turtle, p 1, mid. Point(p 1, p 2), mid. Point(p 1, p 3), depth-1, ) sierpinski(my. Turtle, p 2, mid. Point(p 2, p 3), mid. Point(p 2, p 1), depth-1, ) sierpinski(my. Turtle, p 3, mid. Point(p 3, p 1), mid. Point(p 3, p 2), depth-1, ) else: draw. Triangle(my. Turtle, p 1, p 2, p 3)

Figure 9. 7

Recursive Snowflakes • • Koch Curve L Systems Recursive Grammers Following a sequence of instructions that are recursively generated

Figure 9. 8

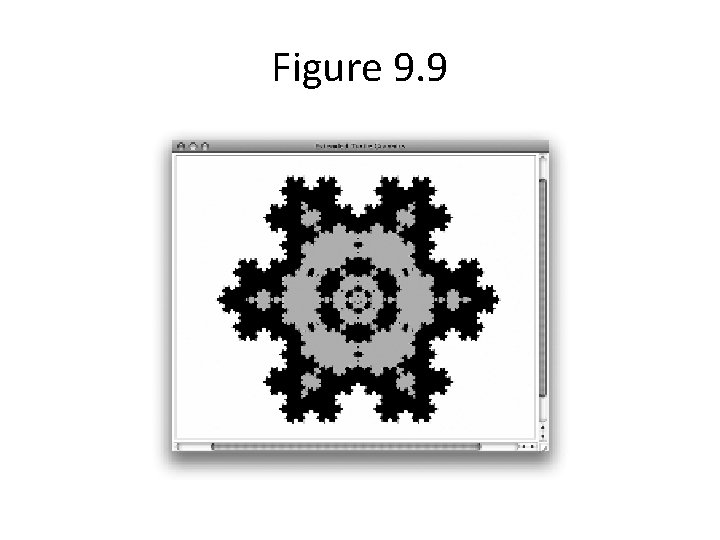
Figure 9. 9

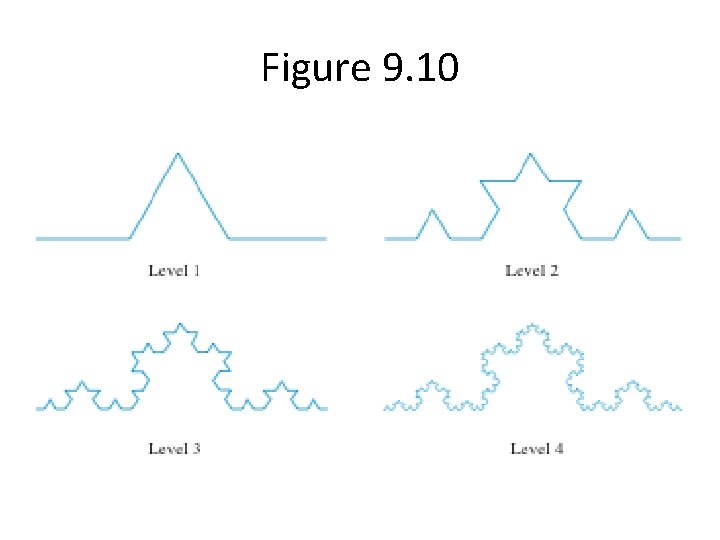
Figure 9. 10

L System • Axiom (starting symbol) • Rules (substitution) Axiom A Rules A → B B → AB

Example A Axiom B (apply rule 1 to A) AB (apply rule 2 to B) BAB (apply rule 1 to A, then apply rule 2 to B) ABBAB (applyrule 2 to B, then rule 1 to A, then rule 2 to B) BABABBAB (rules applied: 1, 2, 2, 1, 2)

Listing 9. 5 def draw. LS(a. Turtle, instructions, angle, distance): for cmd in instructions: if cmd == 'F': a. Turtle. forward(distance) elif cmd == 'B': a. Turtle. backward(distance) elif cmd == '+': a. Turtle. right(angle) elif cmd == '-': a. Turtle. left(angle) else: print('Error: %s is an unknown command'%cmd)

Listing 9. 6 def apply. Production(axiom, rules, n): for i in range(n): new. String = "" for ch in axiom: new. String = new. String + rules. get(ch, ch) axiom = new. String return axiom

Listing 9. 7 def draw. LS(a. Turtle, instructions, angle, distance): state. Saver = [] for cmd in instructions: if cmd == 'F': a. Turtle. forward(distance) elif cmd == 'B': a. Turtle. backward(distance) elif cmd == '+': a. Turtle. right(angle) elif cmd == '-': a. Turtle. left(angle) elif cmd == '[': pos = a. Turtle. position() head = a. Turtle. heading() state. Saver. append((pos, head)) elif cmd == ']': pos, head = state. Saver. pop() a. Turtle. up() a. Turtle. setposition(pos) a. Turtle. setheading(head) a. Turtle. down()

Listing 9. 8 def lsystem(axiom, rules, depth, initial. Position, heading, angle, length): a. Turtle = turtle. Turtle() win = turtle. Screen() a. Turtle. up() a. Turtle. setposition(initial. Position) a. Turtle. down() a. Turtle. setheading(heading) new. Rules = apply. Production(axiom, rules, depth) draw. LS(a. Turtle, new. Rules, angle, length) win. exitonclick()

Figure 9. 11