Python Programming for Engineering Applications Tong Wai Chun

Python Programming for Engineering Applications Tong Wai Chun 15002391 D Project ID: FYP_89 Supervisor: Dr. Isaac Y. F. Fung 1

Introduction Provide a Computer Application for Numerical Computing by Python Programming. Four Numerical Computing Functions are included: 1. Finite-divided Difference Approximate (FDA) 2. Newton’s Interpolating Polynomials (NIP) 3. Classical Fourth Order Runge-Kutta Method (RK) 4. Liebmann’s Method (LM) 2

Background This application is: àCompletely Free àEasy-to-use àNo programming knowledge is needed 3

Objective To develop a free and user-friendly tool: àFor Numerical Computing àFor Learning Purpose àAll computing steps will be shown 4

Methodology Development Environment: Python 3. 6 àFree and Open-source Programming Language àA lot of free packages/libraries have been developed àFor Mathematics, Science, and Engineering Application: àNumpy, Scipy, Matplotlib àFor Graphical User Interface (GUI) Building: àPy. Qt, Tkinter àPython to exe Complier: àPy. Installer 5

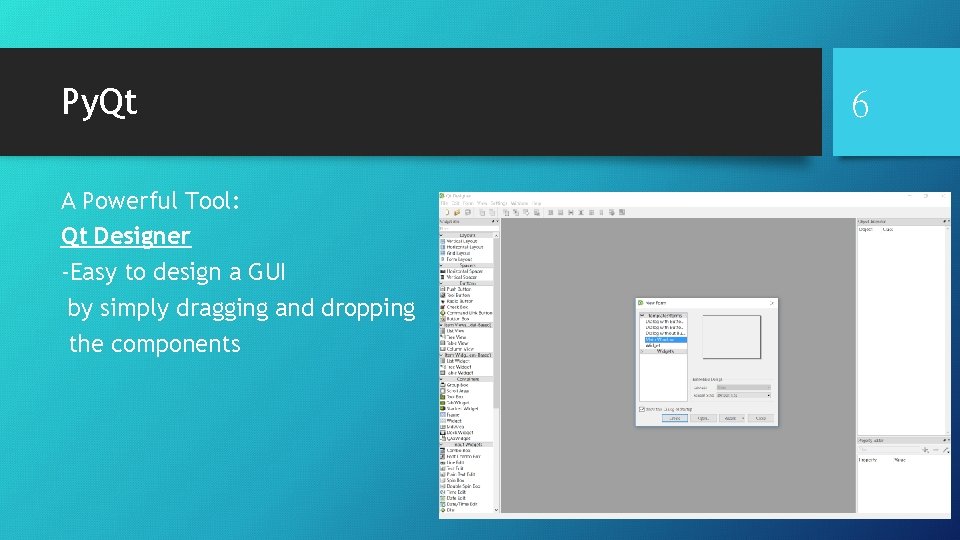
Py. Qt A Powerful Tool: Qt Designer -Easy to design a GUI by simply dragging and dropping the components 6

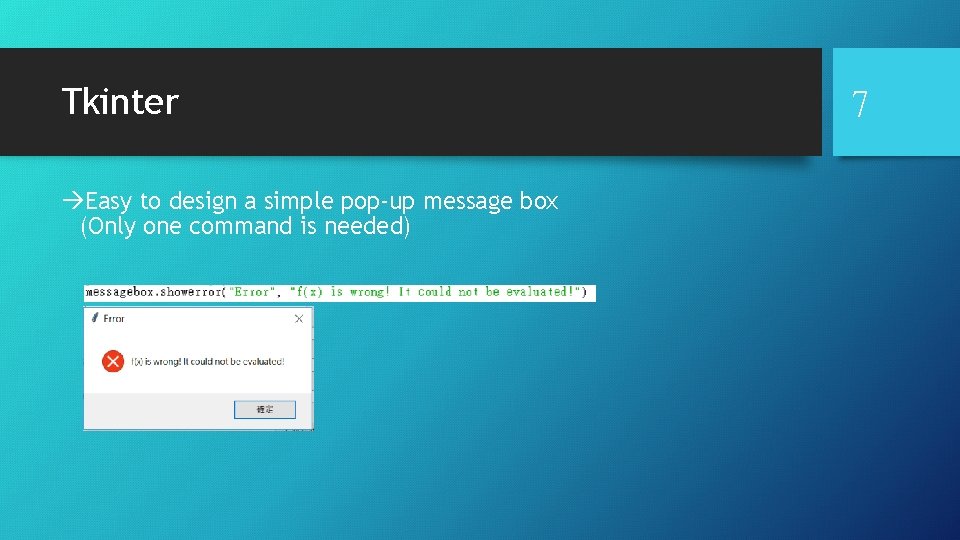
Tkinter àEasy to design a simple pop-up message box (Only one command is needed) 7

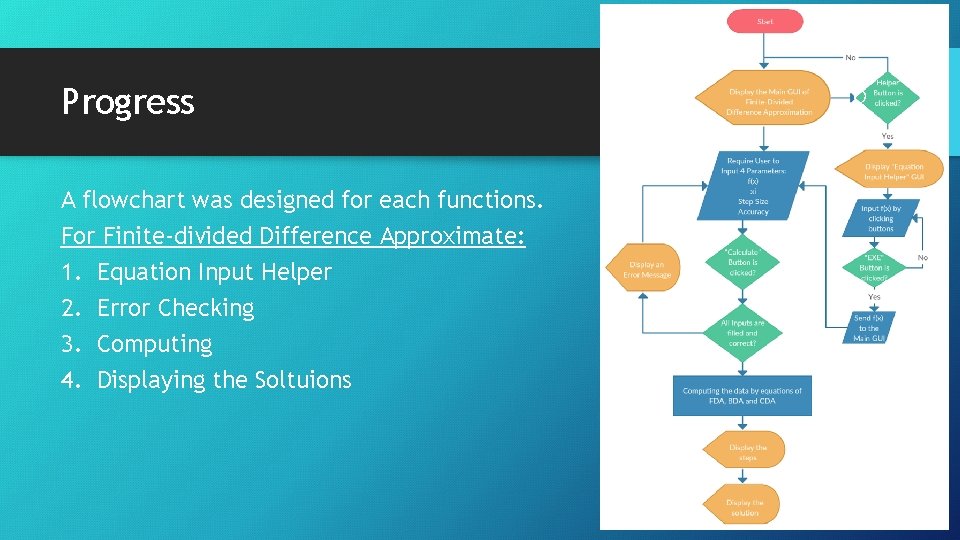
Progress A flowchart was designed for each functions. For Finite-divided Difference Approximate: 1. Equation Input Helper 2. Error Checking 3. Computing 4. Displaying the Soltuions 8

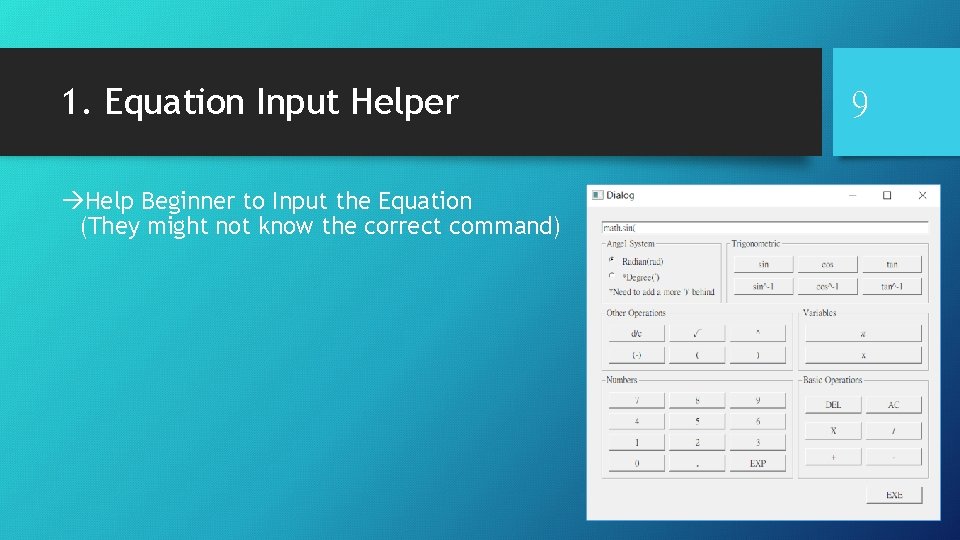
1. Equation Input Helper àHelp Beginner to Input the Equation (They might not know the correct command) 9

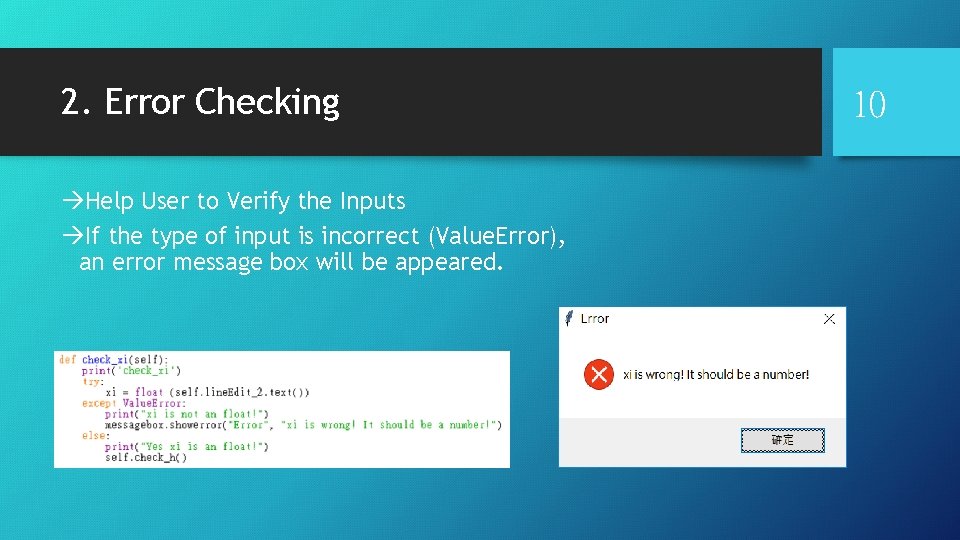
2. Error Checking àHelp User to Verify the Inputs àIf the type of input is incorrect (Value. Error), an error message box will be appeared. 10

3. Computing The Input Data is filled in the equation to compute 11

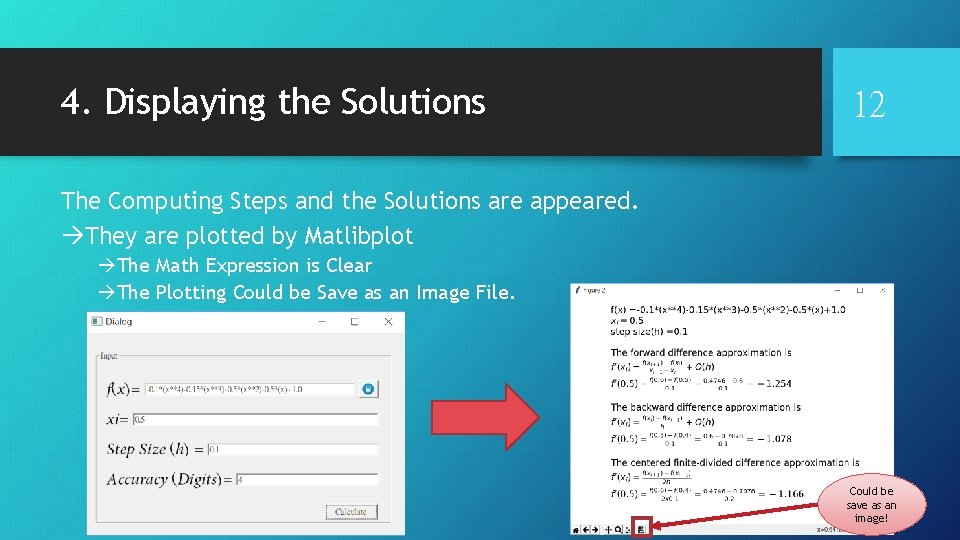
4. Displaying the Solutions 12 The Computing Steps and the Solutions are appeared. àThey are plotted by Matlibplot àThe Math Expression is Clear àThe Plotting Could be Save as an Image File. Could be save as an image!

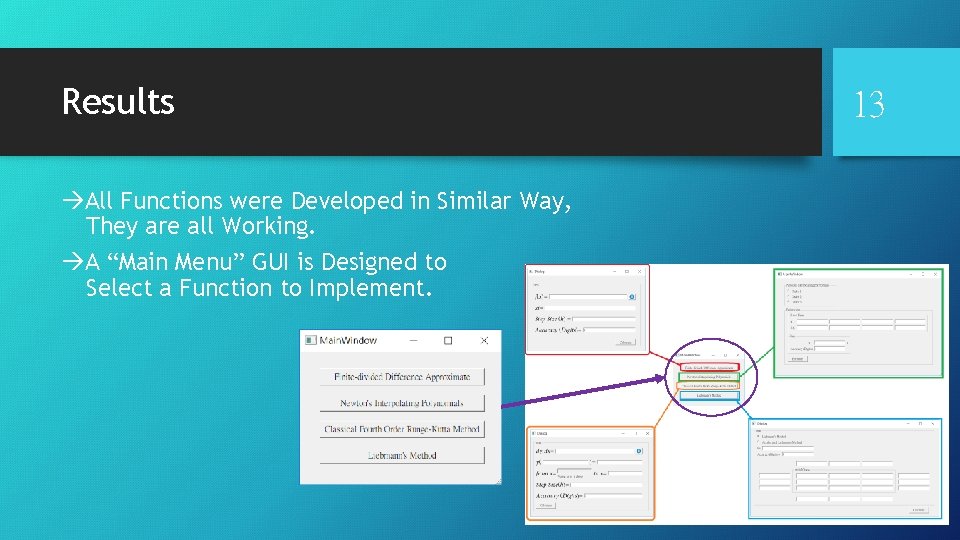
Results àAll Functions were Developed in Similar Way, They are all Working. àA “Main Menu” GUI is Designed to Select a Function to Implement. 13

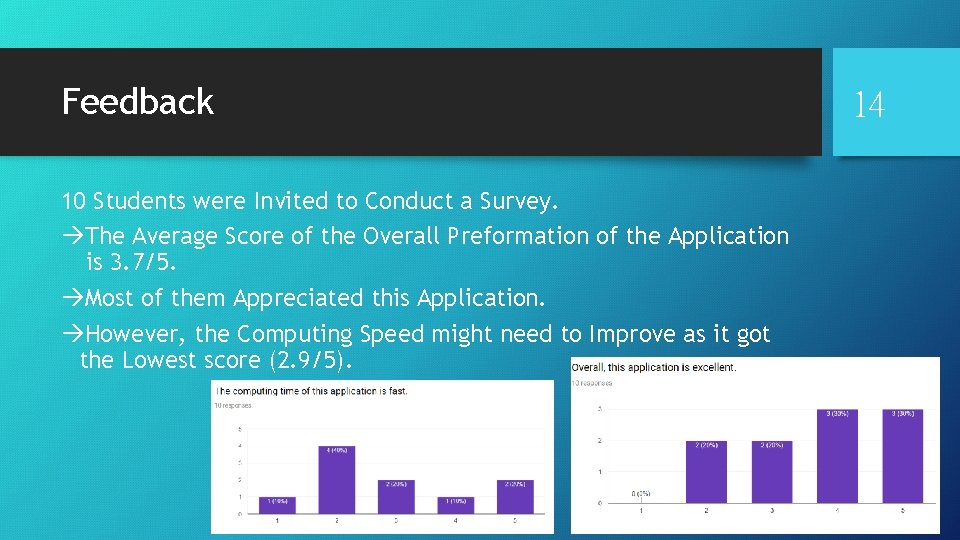
Feedback 10 Students were Invited to Conduct a Survey. àThe Average Score of the Overall Preformation of the Application is 3. 7/5. àMost of them Appreciated this Application. àHowever, the Computing Speed might need to Improve as it got the Lowest score (2. 9/5). 14

Conclusion àAll Proposed Functions were Completed and Working. àMost of the Users Satisfied with this Application. àHas Potential to Further Develop more Functions àBut the Computing Speed might need to Improve. 15

References [1] van Rossum, Guido (20 January 2009). "A Brief Timeline of Python". The History of Python. Google. [Accessed Jan. 4, 2018]. [2] Pythonic Perambulations, Why Python is Slow: Looking Under the Hood [Online]. Available: https: //jakevdp. github. io/blog/2014/05/09/whypython-is-slow/ [Accessed Jan. 4, 2018]. [3] "History and License". Retrieved 5 December 2016. "All Python releases are Open Source" [4] MATLAB & Simulink, Pricing and Licensing [Online]. Available: https: //www. mathworks. com/pricing-licensing. html [Accessed Jan. 4, 2018]. [5] Steinhaus. Stefan, Comparison of mathematical programs for data analysis, 2008 [6] Scilab, Matlab to Scilab Conversion Tips [Online]. Available: https: //help. scilab. org/docs/6. 0. 0/en_US/section_c 592 a 9 ecd 0 ed 2 b 4 d 08 f 8 a 4 de 718 ee 9 aa. html [Accessed Jan. 4, 2018]. [7] Active. State, Python 3 vs Python 2: It’s Different This Time [Online]. Available: https: //help. scilab. org/docs/6. 0. 0/en_US/section_c 592 a 9 ecd 0 ed 2 b 4 d 08 f 8 a 4 de 718 ee 9 aa. html [Accessed Jan. 4, 2018]. [8] Sci. Py, Sci. Py. org — Sci. Py. org [Online]. Available: https: //help. scilab. org/docs/6. 0. 0/en_US/section_c 592 a 9 ecd 0 ed 2 b 4 d 08 f 8 a 4 de 718 ee 9 aa. html [Accessed Jan. 4, 2018]. [9] Python, Tkinter [Online]. Available: https: //wiki. python. org/moin/Tk. Inter [Accessed Jan. 4, 2018]. [10] Enthought, Traits. UI Documentation [Online]. Available: http: //docs. enthought. com/traitsui/ [Accessed Jan. 4, 2018]. 16

References [11] Riverbank Computing Limited, What is Py. Qt? [Online]. Available: https: //riverbankcomputing. com/software/pyqt/intro [Accessed Jan. 4, 2018]. [12] Pierre Raybaut, Win. Python [Online]. Available: http: //winpython. sourceforge. net/ [Accessed Jan. 4, 2018]. [13] Scratch Wiki, Scratch Extension [Online]. Available: https: //wiki. scratch. mit. edu/wiki/Scratch_Extension [Accessed Sep. 24, 2018]. [14] 實體運算樂趣多‧小學教師的學習筆記, 用Python 擴充我的Scratch 2 -- 原 理與Hello World 篇 (Only Chinese version available) [Online]. Available: http: //beardad 1975. blogspot. hk/2015/08/pythonscratch 2 basic. html [Accessed. Apr. 24, 2017]. [15] MIT Media Laboratory, Creating Scratch 2. 0 Extensions [Online]. Available: https: //wiki. scratch. mit. edu/w/images/Extensions. Doc. HTTP-9 -11. pdf [Accessed Jan. 4, 2018]. [16] Num. Py community, Num. Py Reference [Online]. Available: https: //docs. scipy. org/doc/numpy-1. 13. 0/numpy-ref-1. 13. 0. pdf [Accessed Jan. 4, 2018]. [17] Sci. Py community, Sci. Py Reference Guide [Online]. Available: https: //docs. scipy. org/doc/numpy-1. 13. 0/numpy-ref-1. 13. 0. pdf [Accessed Jan. 4, 2018]. [18] Michael Waskom, seaborn: statistical data visualization [Online]. Available: https: //seaborn. pydata. org/ [Accessed Mar. 28, 2018]. [19] Py. FPDF, FPDF for Python [Online]. Available: https: //pyfpdf. readthedocs. io/en/latest/ [Accessed Mar. 28, 2018]. [20] Pyerclip, Introduction [Online]. Available: http: //pyperclip. readthedocs. io/en/latest/introduction. html [Accessed Mar. 29, 2018]. 17

References [21] Py. Installer, Welcome to Py. Installer official website [Online]. Available: https: //www. pyinstaller. org/ [Accessed Mar. 29, 2018]. [22] cx_Freeze, About cx_Freeze [Online]. Available: https: //anthony-tuininga. github. io/cx_Freeze/ [Accessed Mar. 29, 2018]. [23] Paul Wilmott; Sam Howison; Jeff Dewynne (1995). The Mathematics of Financial Derivatives: A Student Introduction. Cambridge University Press. p. 137. [24] Peter Olver (2013). Introduction to Partial Differential Equations. Springer Science & Business Media. [25] M Hanif Chaudhry (2007). Open-Channel Flow. Springer. p. 369. [26] Indian Institute of Technology, Newton Interpolation polynomial [Online]. Available: http: //nptel. ac. in/courses/122104019/numerical-analysis/Rathish-kumar/rathish-oct 31/fratnode 5. html [Accessed Mar. 28, 2018]. [27] Süli, Endre; Mayers, David (2003), An Introduction to Numerical Analysis, Cambridge University Press [28] Steven C. Chapra, Raymond P. Canale (2013). Numerical Methods for Engineers (6 th Edition). Mc. Graw-Hill Education. 18