Pythagorean Theorem Nama Mark Anthony M IIB BSE
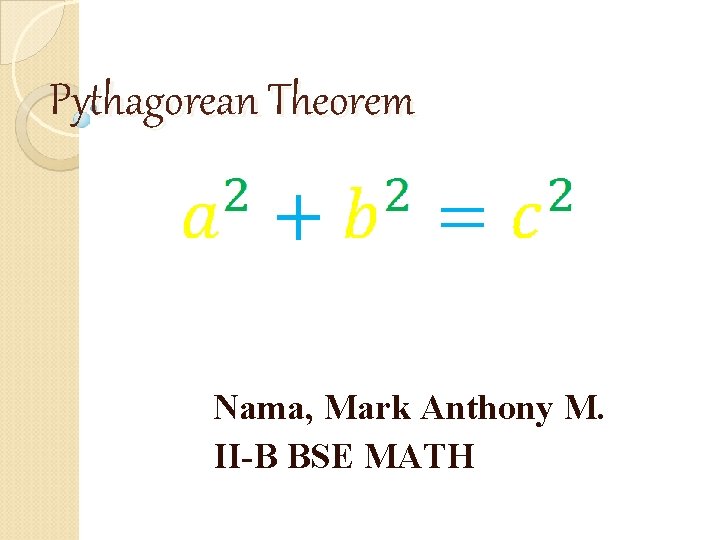
Pythagorean Theorem Nama, Mark Anthony M. II-B BSE MATH

PYTHAGOREAN THEOREM – used to find the measures of one side of a right triangle, if the measures of the other two sides are known.

It was named after the Greek mathematician Pythagoras. The Pythagorean theorem can be used to find the measure of one side of a right triangle if the measures of the other sides are known.
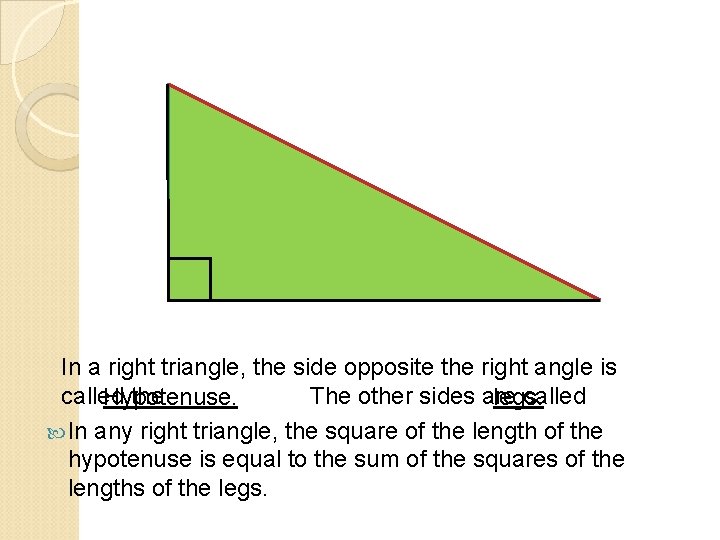
In a right triangle, the side opposite the right angle is called the The other sides are called Hypotenuse. legs. In any right triangle, the square of the length of the hypotenuse is equal to the sum of the squares of the lengths of the legs.

A c b C a In B right triangle ABC, where c is the length of the hypotenuse, and a and b are lengths of the legs. Therefore, c 2=a 2+b 2

PROOF
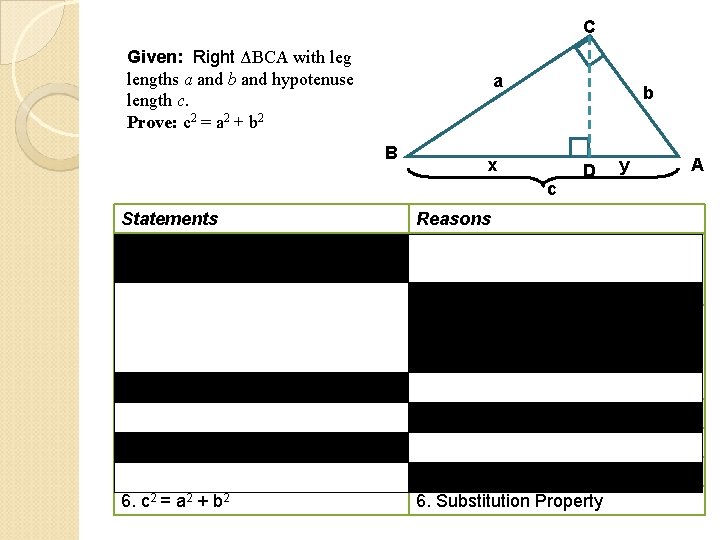
C Given: Right ΔBCA with leg lengths a and b and hypotenuse length c. Prove: c 2 = a 2 + b 2 a B b x c D y A Statements Reasons 1. Draw altitude CD to the hypotenuse 1. From a point not on a line, exactly one ┴can be drawn to the line. 2. The length of each leg is the geom. mean between the length of its adjacent seg. of the hypotenuse and the entire hypotenuse 3. cx = a 2; cy = b 2 3. Means – extremes Property 4. cx + cy = a 2 + b 2 4. Addition Property 5. c(x + y) = a 2 + b 2 5. Distributive Property 6. c 2 = a 2 + b 2 6. Substitution Property

EXAMPLES
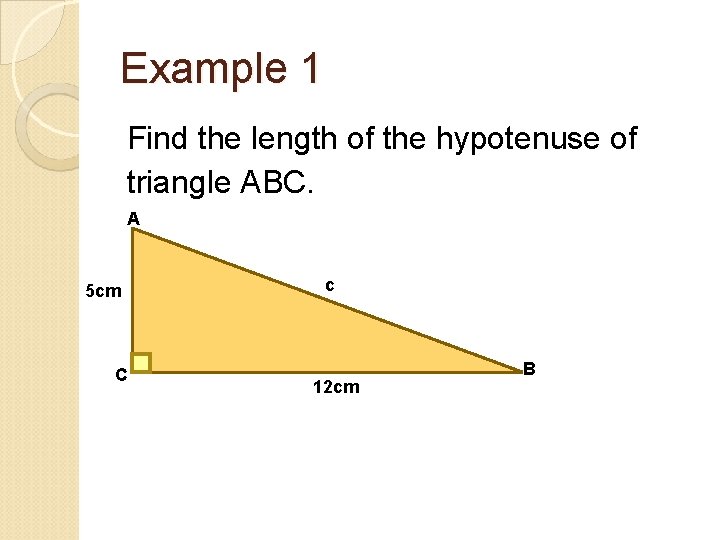
Example 1 Find the length of the hypotenuse of triangle ABC. A 5 cm C c 12 cm B

Solution c 2 = a 2 + b 2 c 2 = 52 + 122 c 2 = 25 + 144 c 2 = 169 c= c = 13 cm
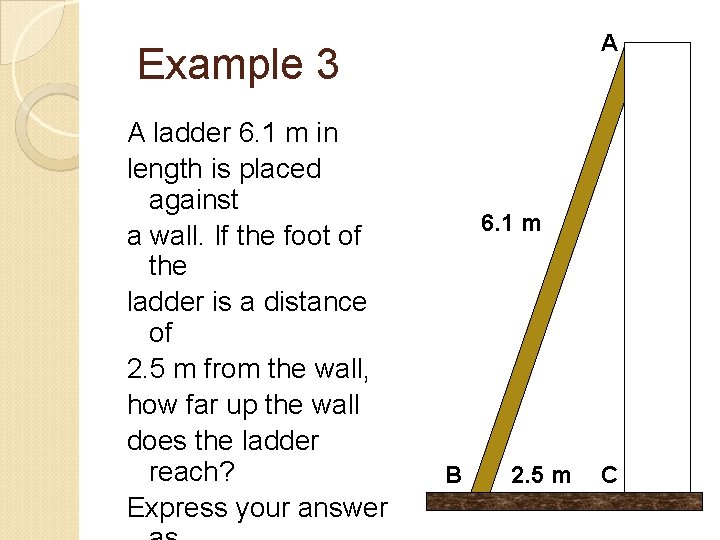
A Example 3 A ladder 6. 1 m in length is placed against a wall. If the foot of the ladder is a distance of 2. 5 m from the wall, how far up the wall does the ladder reach? Express your answer 6. 1 m B 2. 5 m C

Solution c 2 = a 2 + b 2 6. 12 = 2. 52 + b 2 37. 31 = 6. 25 + b 2 = 37. 31 – 6. 25 b 2 = 30. 96 b 2 = b ≈ 5. 6 m

THE END
- Slides: 13