PYTHAGORE VOUS AVEZ DIT THEOREME DE PYTHAGORE ACTIVITE

PYTHAGORE ! VOUS AVEZ DIT THEOREME DE PYTHAGORE

ACTIVITE PREPARATOIRE

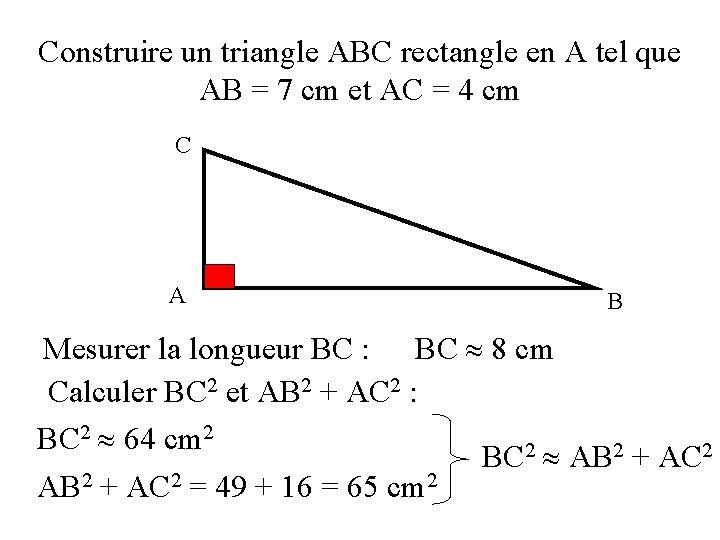
Construire un triangle ABC rectangle en A tel que AB = 7 cm et AC = 4 cm C A B Mesurer la longueur BC : BC 8 cm Calculer BC 2 et AB 2 + AC 2 : BC 2 64 cm 2 BC 2 AB 2 + AC 2 = 49 + 16 = 65 cm 2

CLIQUEZ ICI : GEOPLANW

UTILITE DU THEOREME DE PYTHAGORE Le théorème de PYTHAGORE permet de déterminer la longueur du coté d’un triangle rectangle connaissant la longueur des deux autres cotés. B A C

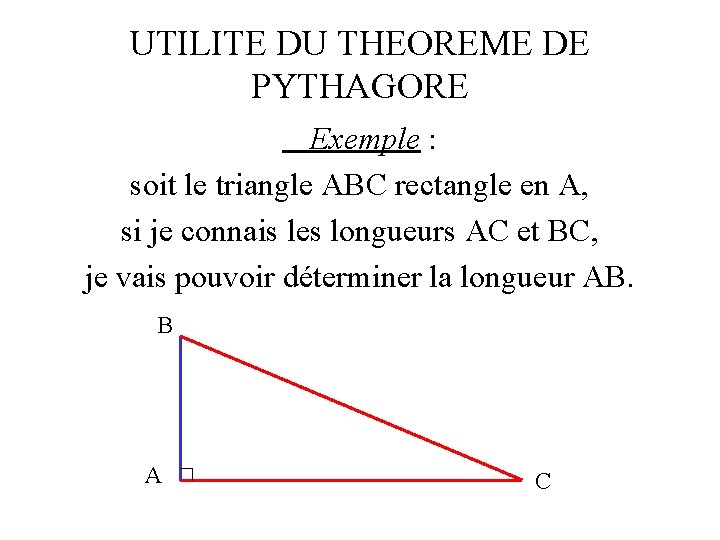
UTILITE DU THEOREME DE PYTHAGORE Exemple : soit le triangle ABC rectangle en A, si je connais les longueurs AC et BC, je vais pouvoir déterminer la longueur AB. B A C

L’HYPOTENUSE ?

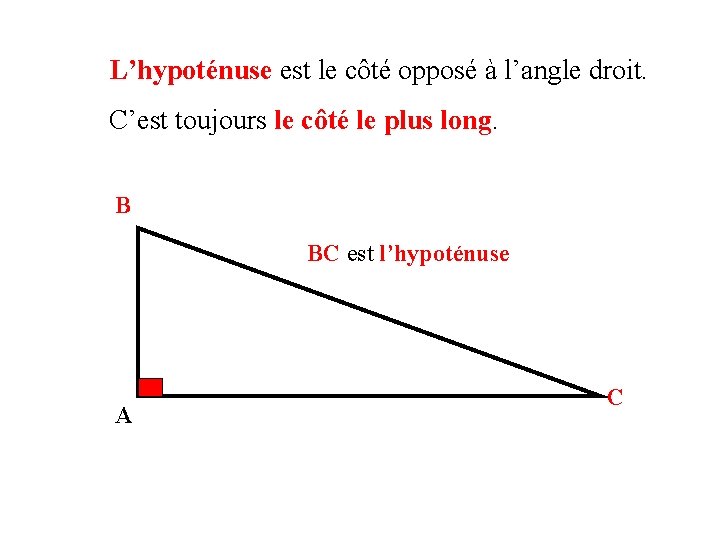
L’hypoténuse est le côté opposé à l’angle droit. C’est toujours le côté le plus long. B BC est l’hypoténuse A C

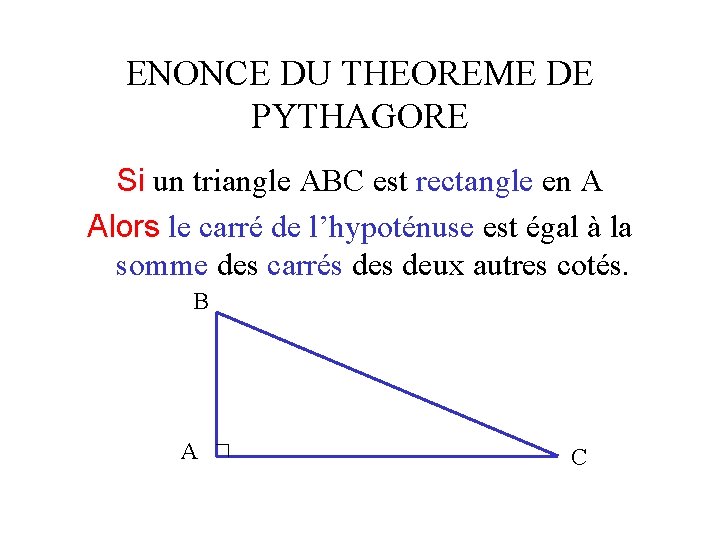
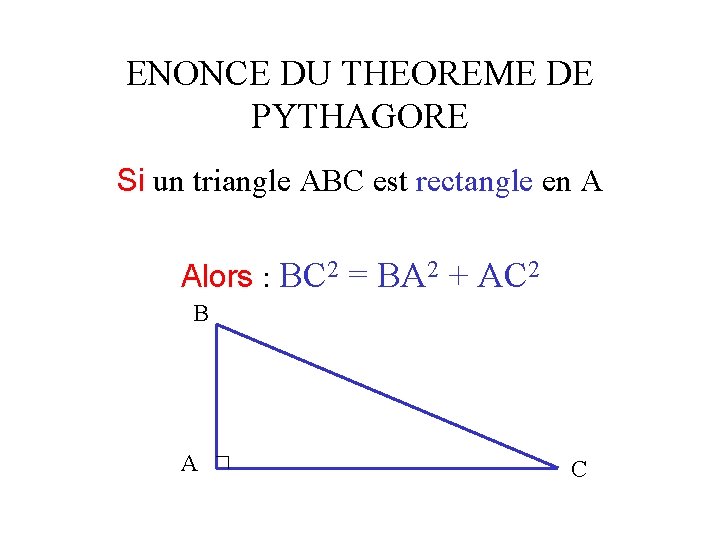
ENONCE DU THEOREME DE PYTHAGORE Si un triangle ABC est rectangle en A Alors le carré de l’hypoténuse est égal à la somme des carrés deux autres cotés. B A C

ENONCE DU THEOREME DE PYTHAGORE Si un triangle ABC est rectangle en A Alors : BC 2 = BA 2 + AC 2 B A C

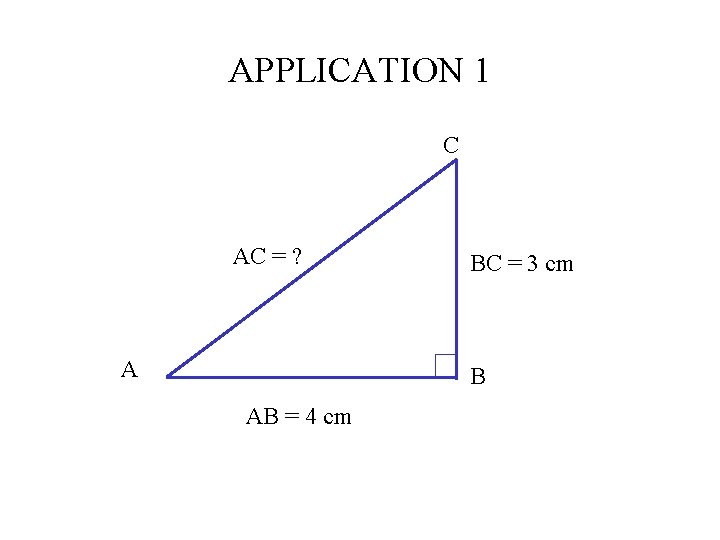
APPLICATION 1 Soit le triangle ABC rectangle en B. On donne AB = 4 cm et BC = 3 cm Calculer AC. C A B

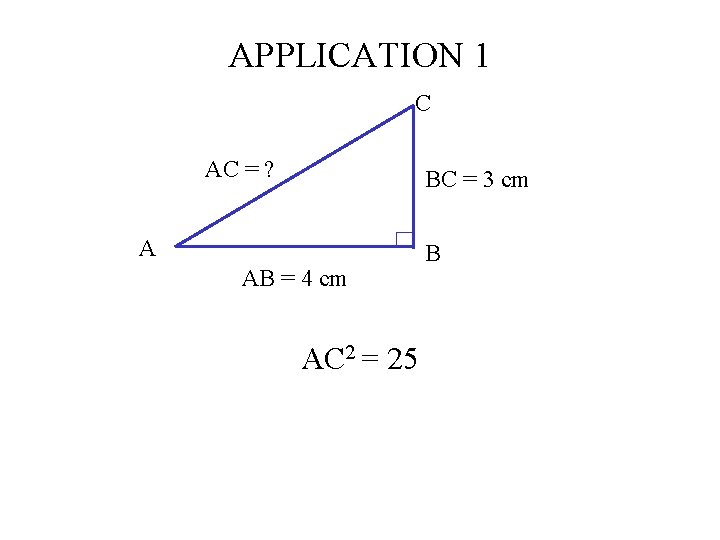
APPLICATION 1 C AC = ? A BC = 3 cm B AB = 4 cm

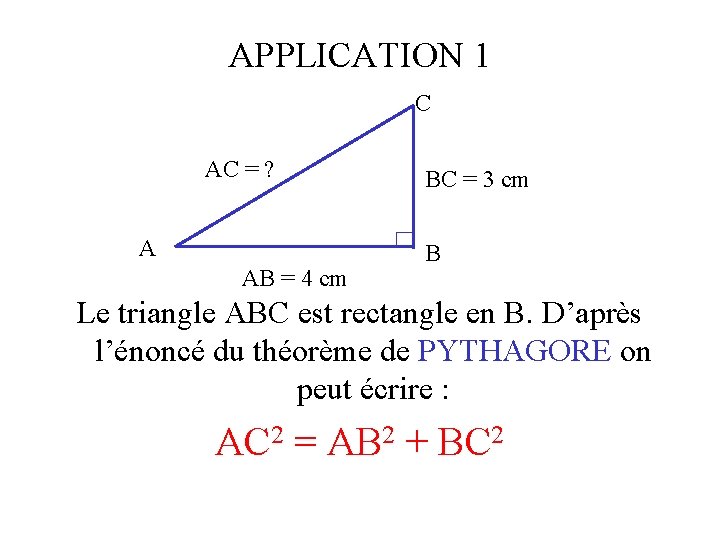
APPLICATION 1 C AC = ? A AB = 4 cm BC = 3 cm B Le triangle ABC est rectangle en B. D’après l’énoncé du théorème de PYTHAGORE on peut écrire : AC 2 = AB 2 + BC 2

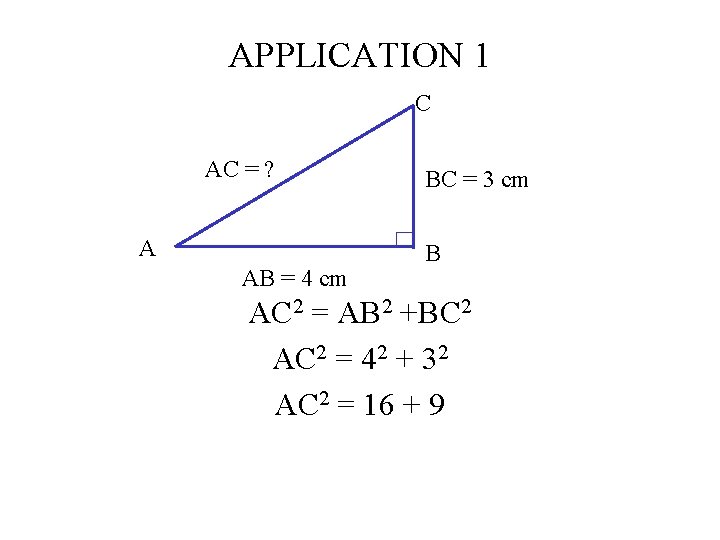
APPLICATION 1 C AC = ? A AB = 4 cm BC = 3 cm B AC 2 = AB 2 +BC 2 AC 2 = 42 + 32 AC 2 = 16 + 9

APPLICATION 1 C AC = ? BC = 3 cm A AB = 4 cm AC 2 = 25 B

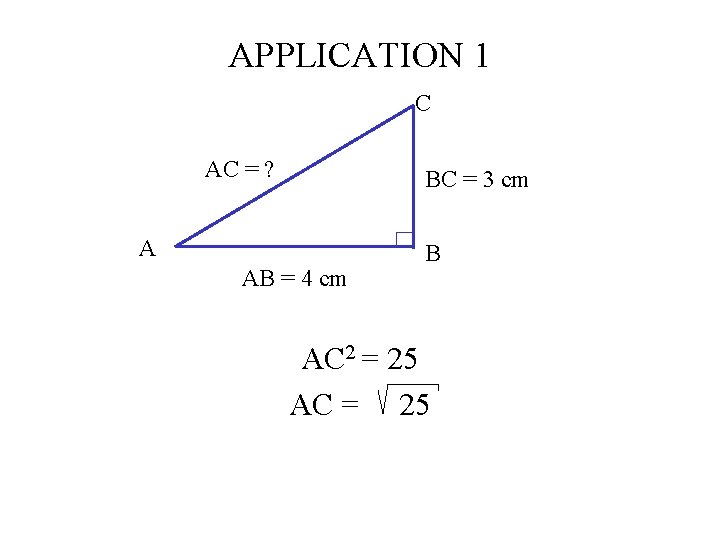
APPLICATION 1 C AC = ? BC = 3 cm A AB = 4 cm B AC 2 = 25 AC = 25

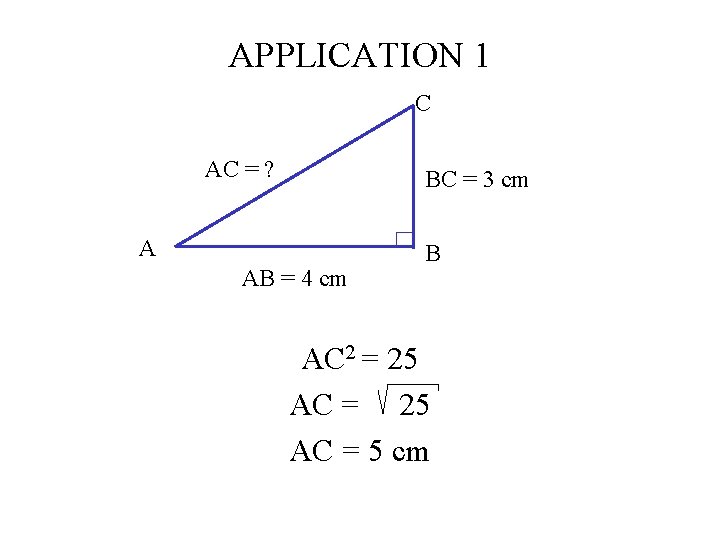
APPLICATION 1 C AC = ? BC = 3 cm A AB = 4 cm B AC 2 = 25 AC = 5 cm

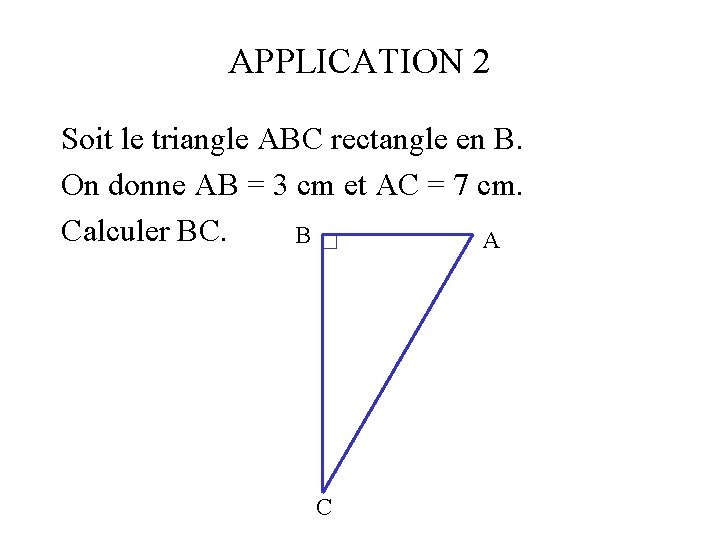
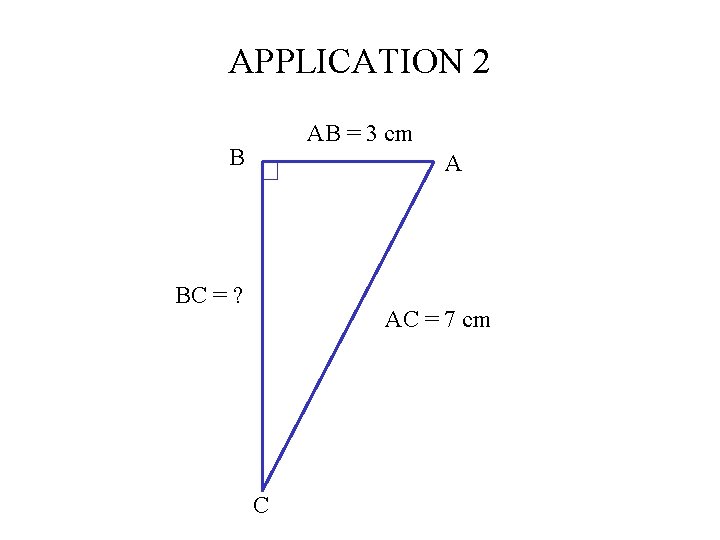
APPLICATION 2 Soit le triangle ABC rectangle en B. On donne AB = 3 cm et AC = 7 cm. Calculer BC. B A C

APPLICATION 2 AB = 3 cm B A BC = ? AC = 7 cm C

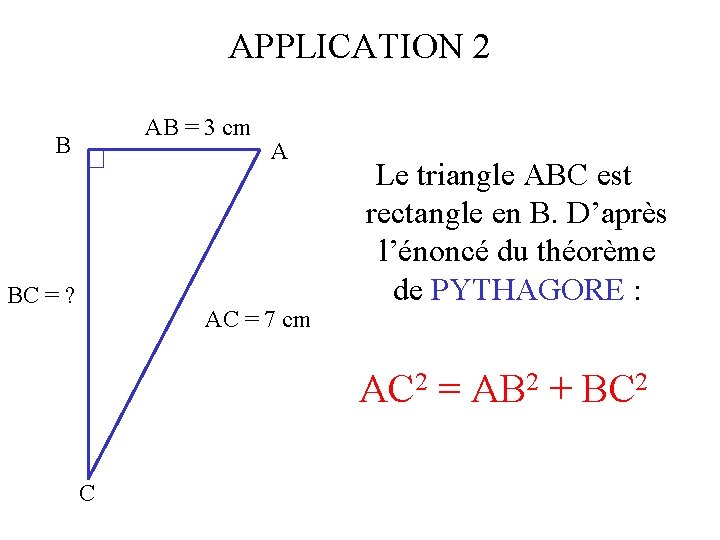
APPLICATION 2 AB = 3 cm B BC = ? A AC = 7 cm Le triangle ABC est rectangle en B. D’après l’énoncé du théorème de PYTHAGORE : AC 2 = AB 2 + BC 2 C

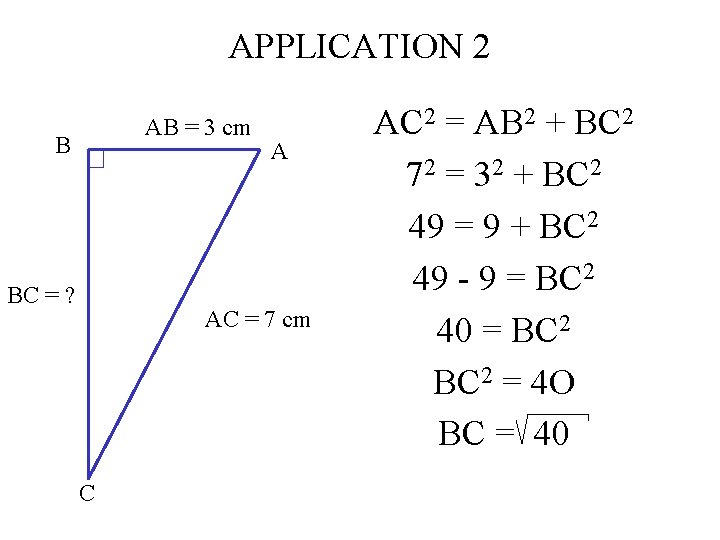
APPLICATION 2 AB = 3 cm B BC = ? A AC = 7 cm C AC 2 = AB 2 + BC 2 72 = 32 + BC 2 49 = 9 + BC 2 49 - 9 = BC 2 40 = BC 2 = 4 O

APPLICATION 2 AB = 3 cm B BC = ? A AC = 7 cm C AC 2 = AB 2 + BC 2 72 = 32 + BC 2 49 = 9 + BC 2 49 - 9 = BC 2 40 = BC 2 = 4 O BC = 40

APPLICATION 2 AB = 3 cm B BC = ? A AC = 7 cm C AC 2 = AB 2 + BC 2 72 = 32 + BC 2 49 = 9 + BC 2 49 - 9 = BC 2 40 = BC 2 = 4 O BC = 40 BC 6, 32 cm

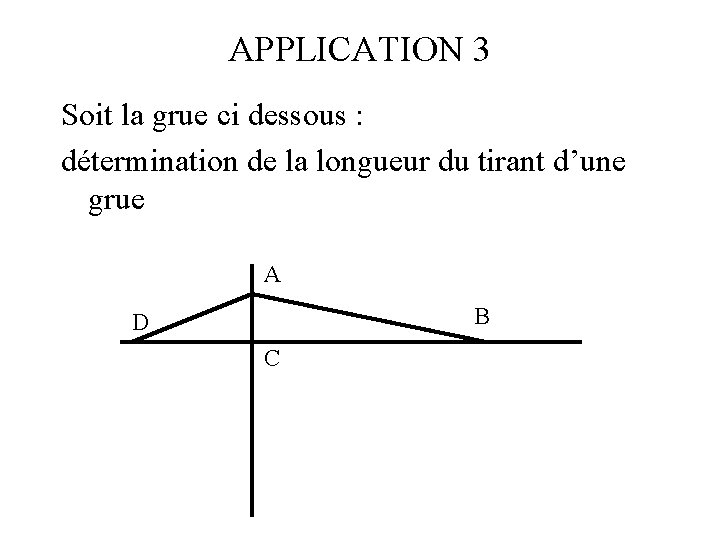
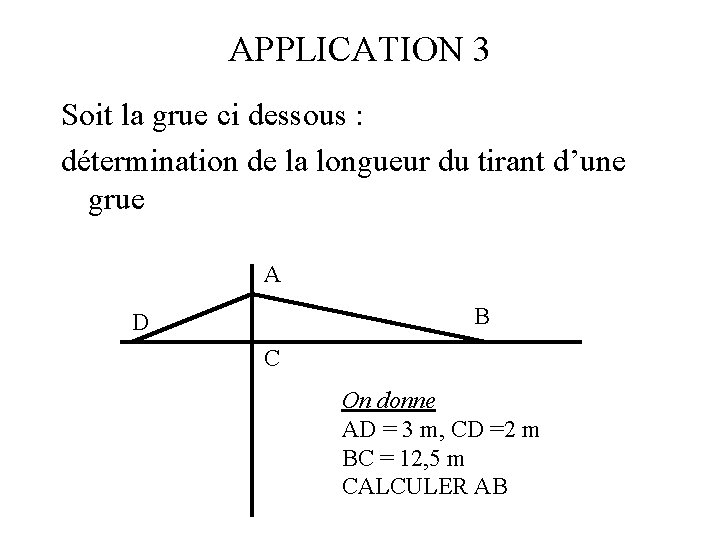
APPLICATION 3 Soit la grue ci dessous : détermination de la longueur du tirant d’une grue A B D C

APPLICATION 3 Soit la grue ci dessous : détermination de la longueur du tirant d’une grue A B D C On donne AD = 3 m, CD =2 m BC = 12, 5 m CALCULER AB

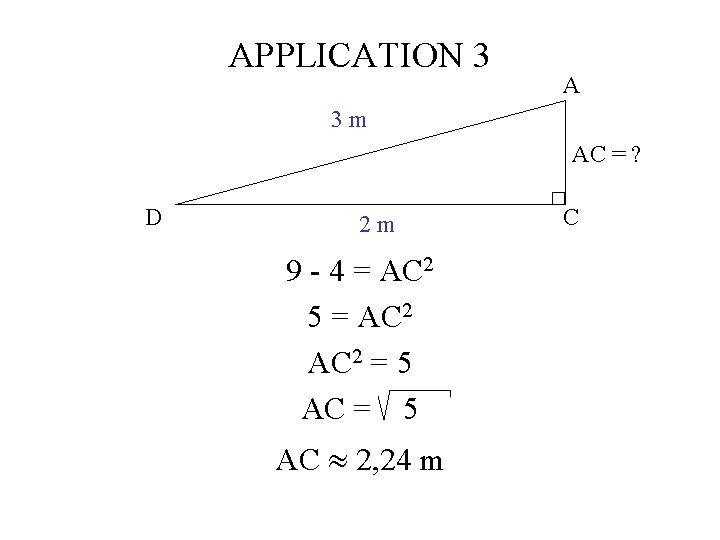
APPLICATION 3 A 3 m AB = ? D 2 m C B 12, 5 m On calcule d’abord AC

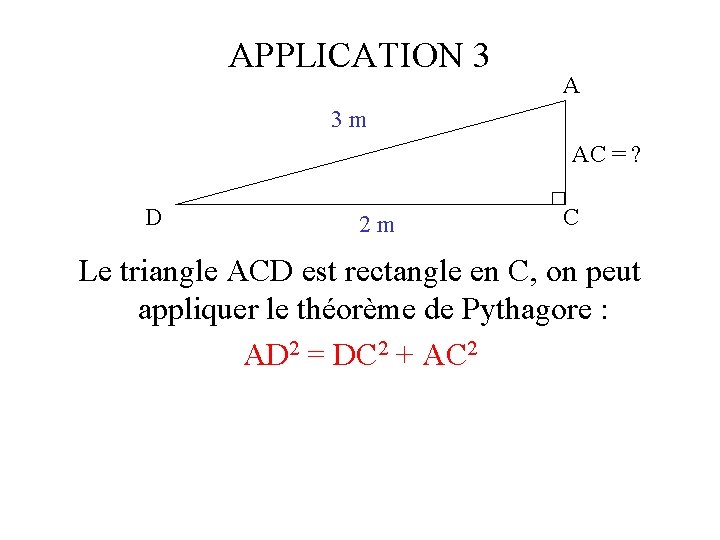
APPLICATION 3 A 3 m AC = ? D 2 m C Le triangle ACD est rectangle en C, on peut appliquer le théorème de Pythagore : AD 2 = DC 2 + AC 2

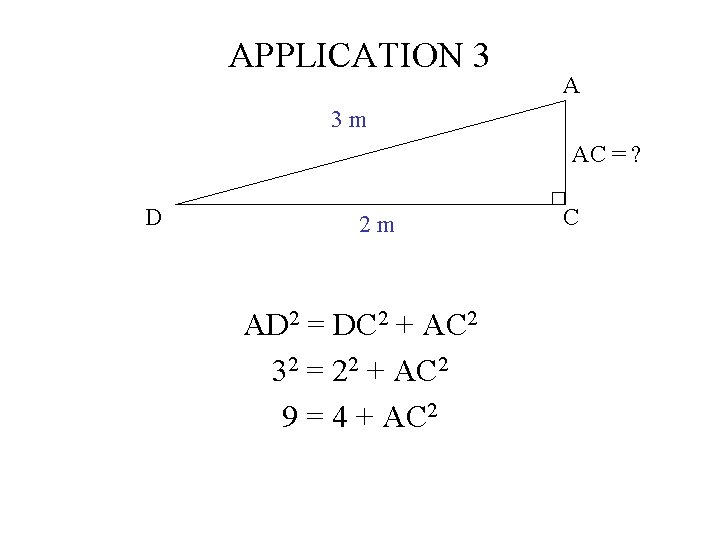
APPLICATION 3 A 3 m AC = ? D 2 m AD 2 = DC 2 + AC 2 32 = 22 + AC 2 9 = 4 + AC 2 C

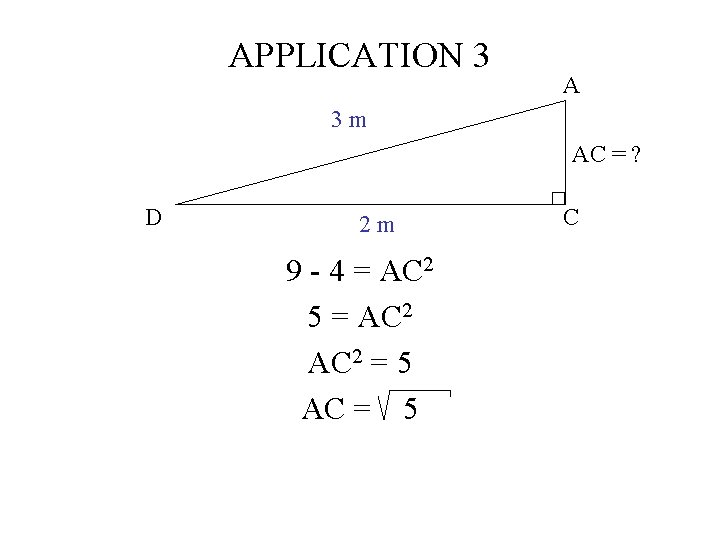
APPLICATION 3 A 3 m AC = ? D 2 m 9 - 4 = AC 2 5 = AC 2 = 5 C

APPLICATION 3 A 3 m AC = ? D 2 m 9 - 4 = AC 2 5 = AC 2 = 5 AC = 5 C

APPLICATION 3 A 3 m AC = ? D 2 m 9 - 4 = AC 2 5 = AC 2 = 5 AC 2, 24 m C

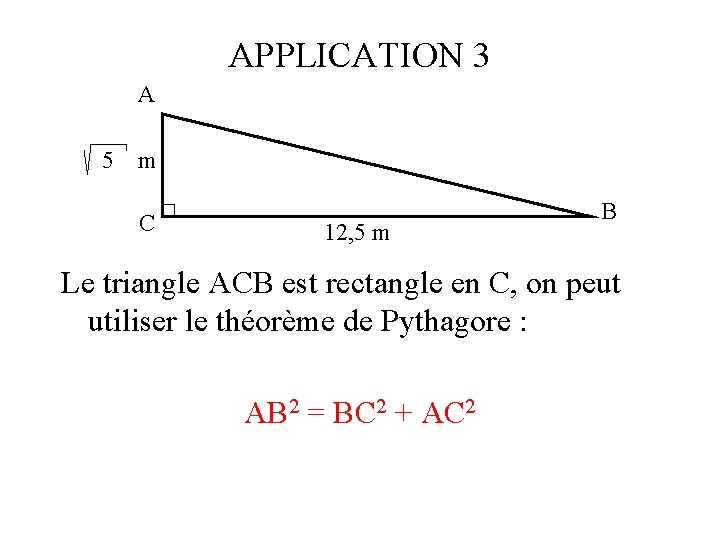
APPLICATION 3 A 5 m C 12, 5 m B Le triangle ACB est rectangle en C, on peut utiliser le théorème de Pythagore : AB 2 = BC 2 + AC 2

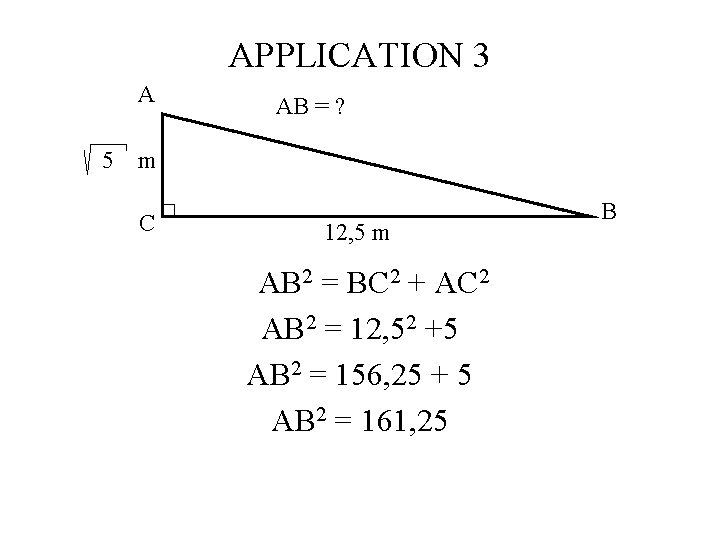
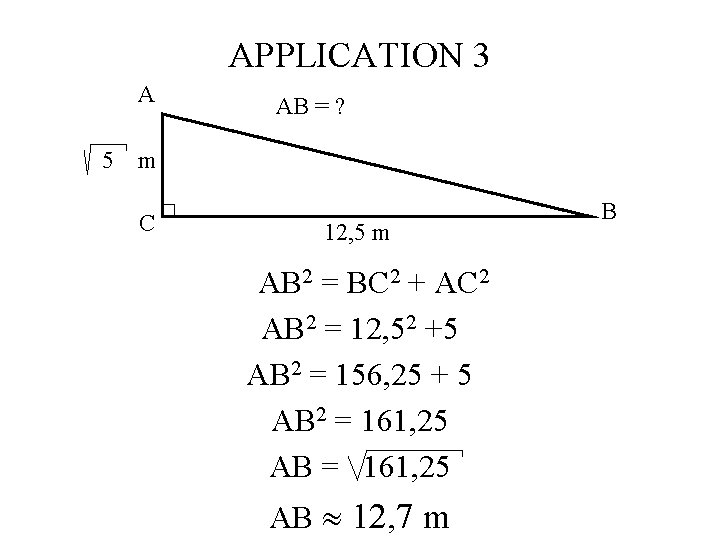
APPLICATION 3 A 5 AB = ? m C 12, 5 m AB 2 = BC 2 + AC 2 AB 2 = 12, 52 +5 AB 2 = 156, 25 + 5 AB 2 = 161, 25 B

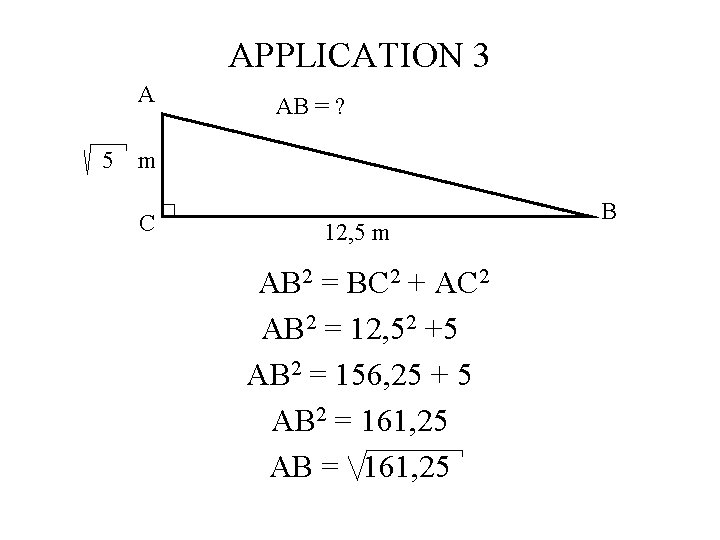
APPLICATION 3 A 5 AB = ? m C 12, 5 m AB 2 = BC 2 + AC 2 AB 2 = 12, 52 +5 AB 2 = 156, 25 + 5 AB 2 = 161, 25 AB = 161, 25 B

APPLICATION 3 A 5 AB = ? m C 12, 5 m AB 2 = BC 2 + AC 2 AB 2 = 12, 52 +5 AB 2 = 156, 25 + 5 AB 2 = 161, 25 AB 12, 7 m B

POUR EN SAVOIR PLUS Pour démontrer le théorème de Pythagore on peut utiliser la méthode suivante : Soit deux carrés de cotés différents placés comme indiqué sur la figure cicontre :

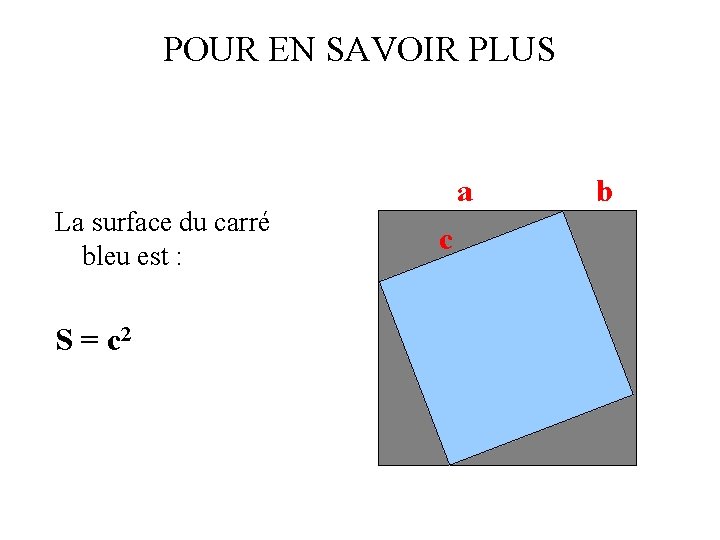
POUR EN SAVOIR PLUS La surface du carré bleu est : a c b

POUR EN SAVOIR PLUS La surface du carré bleu est : S = c 2 a c b

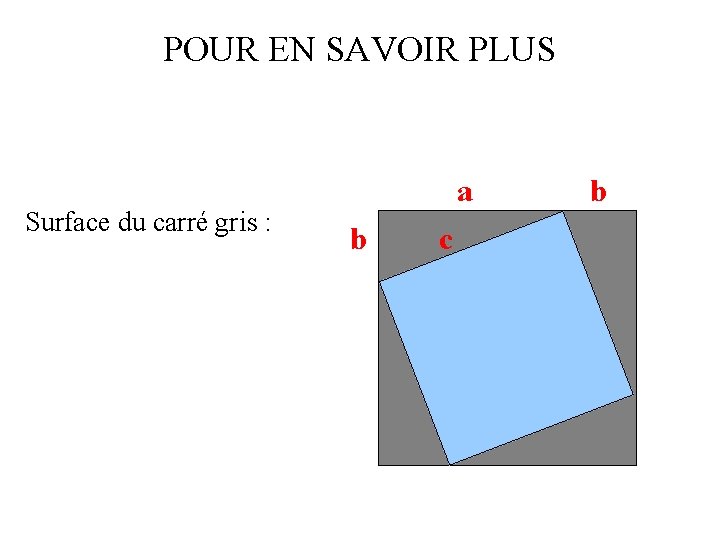
POUR EN SAVOIR PLUS Cette surface peut également se calculer à l’aide de l’aire du carré gris et celles des quatre triangles de cotés a, b, c. a b c

POUR EN SAVOIR PLUS Surface du carré gris : a b c b

POUR EN SAVOIR PLUS Surface du carré gris : (a + b)2 = a b c b

POUR EN SAVOIR PLUS Surface du carré gris : (a + b)2 = a 2 + b 2 + 2 ab a b c b

POUR EN SAVOIR PLUS Surface du carré gris : (a + b)2 = a 2 + b 2 + 2 ab a b Surface des quatre triangles : c b

POUR EN SAVOIR PLUS Surface du carré gris : (a + b)2 = a 2 + b 2 + 2 ab a b Surface des quatre triangles : 4 (a b) 2 = c b

POUR EN SAVOIR PLUS Surface du carré gris : (a + b)2 = a 2 + b 2 + 2 ab a b Surface des quatre triangles : 4 (a b) 2 = 2 ab c b

POUR EN SAVOIR PLUS Surface du carré bleu : S = a 2 + b 2 + 2 ab - 2 ab S = a 2 + b 2 a b c b

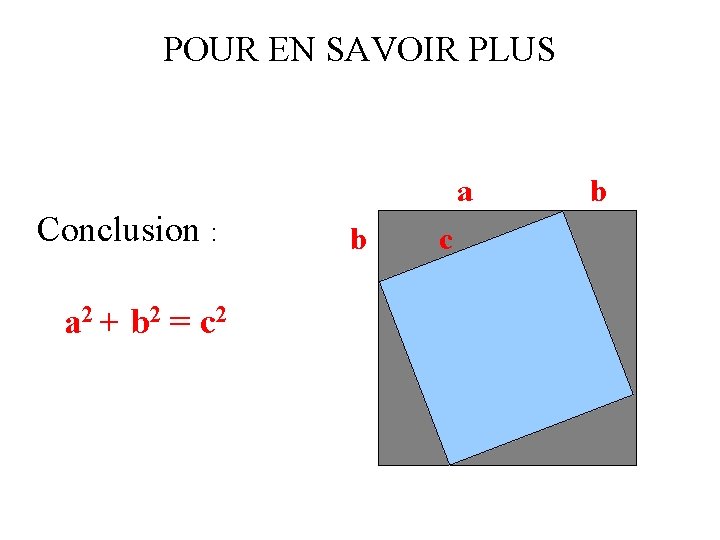
POUR EN SAVOIR PLUS a Conclusion : a 2 + b 2 = c 2 b c b